基于截面折减系数的桥梁结构刚度退化分析

罗 驰

（珠海市交通工程质量监测站,广东 珠海 519000）

0 引言

运营桥梁整体刚度退化主要成因为混凝土材料的风化、碳化、物理与化学损伤，以及钢筋及预应力束有效面积的损失。桥梁刚度退化可以从侧面反映出桥梁的健康状况[1]，结构的刚度退化将会影响桥梁的受力性能和承载能力，后期将会对桥梁结构埋下安全隐患。在桥梁承载能力评定中，混凝土及钢筋损伤程度通常以圬工及配筋混凝土桥梁截面折减系数、配筋混凝土钢筋截面折减系数定量表示，但对于桥梁结构刚度退化程度未进行定量分析。该文通过有限元分析及工程实例验证，建立桥梁构件截面折减系数与结构整体刚度退化的数学模型，为结构刚度退化定量分析提供依据。

1 运营桥梁结构刚度退化评定的两种方法

运营桥梁评定主要有桥梁承载能力评定及荷载试验。桥梁承载能力评定主要是依据交通运输部《公路桥梁承载能力评定规程》（JTG/T J21—2011），基于桥梁结构技术状况检测结果，对桥梁构件缺损情况、材质状况指标以及实际运营荷载状况进行评定。以基于概率理论的极限状态设计方法为基础，采用引入分项检算系数修正极限状态设计表达式的方法，对在用桥梁承载能力进行检测评定[2]。桥梁荷载试验主要是依据交通运输部《公路桥梁荷载试验规程》（JTG/T J21—01—2015），通过施加荷载方式对桥梁结构或构件的静、动力特性进行的现场试验测试。包括静载试验和动载试验。桥梁荷载试验通过静载试验和动载试验判断桥梁结构的刚度是否满足要求，是否处于弹性工作阶段，对在设计移动荷载作用下桥梁结构承载能力是否满足要求进行定性判断，但不能定量地得到桥梁结构准确的极限承载能力，是桥梁承载能力评定的组成部分。而桥梁承载能力评定是基于结构的技术状况检查，通过对桥梁结构在恒载、移动荷载、温度、支点沉降等各种作用下承载能力极限状态和正常使用极限状态的检算，得出桥梁结构的准确极限承载能力，是桥梁承载能力的定量和定性判断[3]。

该文通过借鉴公路桥梁承载能力评定中对桥梁构件截面折减系数的定量检算，建立桥梁构件截面折减系数与结构整体刚度退化的数学模型，结合莲溪大桥荷载试验的工程实例桥对试验孔自振频率进行桥结构整体刚度的退化分析，验证退化模型的实用性。

2 桥梁刚度退化的特征值计算方法

特征值分析常用于分析结构固有的动力特性[3]，对于无阻尼自由振动的运动方程进行二阶微分得到平衡方程：

式中，K——结构的刚度矩阵；M——结构的质量矩阵。

在有限元法的特征分析中，将连续体划分成许多单元，建立结构的刚度矩阵及质量矩阵，将求解特征值问题变成以下方程的求解：

结构的振型可以反映结构质量分布、刚度分布，因此通过分析振型能够有效地判断结构的质量分布、刚度分布，以及边界条件。通过对有限元模型中计算参数的调整模拟圬工及钢筋混凝土桥梁截面折减系数ξc和钢筋混凝土钢筋截面折减系数ξS对混凝土及钢筋截面折减的影响，见表1和表2。其中依据材料风化、碳化、物理与化学损伤三项检测指标得到截面损伤综合评定标度R，从而得到截面折减系数ξc，依据构件沿钢筋出现裂缝形态、表面膨胀性锈层、锈蚀剥落、钢筋截面损伤等得到钢筋截面折减系数ξS[4]。根据材料力学计算公式，得到折减系数ξc和ξS对截面刚度矩阵的影响系数见表3和表4。

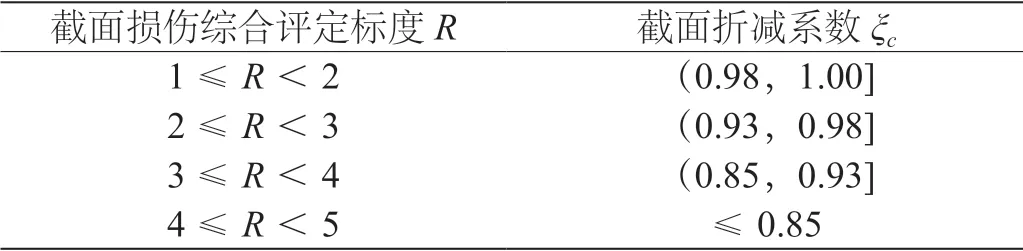
表1 圬工与配筋混凝土梁截面折减系数ξc值

表2 配筋混凝土钢筋截面折减系数ξS值

表3 桥梁截面折减系数对截面刚度矩阵的影响系数表

表4 钢筋截面折减系数对截面刚度矩阵的影响系数表

3 工程概况

莲溪大桥位于珠海市斗门区S272肇珠线，建成年代为1992年，桥梁跨越赤粉水道，旧桥设计时为Ⅳ级航道。莲溪大桥全长414 m，其中跨径总长410 m，最大单孔跨径45 m，桥梁全宽8.6 m，桥面净宽8.0 m。上部结构形式为45 m预应力钢筋混凝土T梁和16 m普通钢筋混凝土T梁，桥墩为双柱式墩，跨径组合为10×16 m+2×45 m+10×16 m。支座为板式橡胶支座，伸缩缝形式为仿毛勒式伸缩缝，桥面铺装形式为混凝土桥面。该次荷载试验选取第11跨单孔跨径45 m进行静载试验和动载试验，静载试验测试主要内容包括：①梁体变形；②控制截面底面、顶面及侧面应变；③裂缝观测；④支座沉降观测；⑤残余挠度及应变。动载试验内容包括：①地脉动试验；②跑车试验；③跳车试验。

莲溪大桥第11跨T梁桥梁主要病害普遍存在的缺损现象为：少数T梁梗腋存在纵向裂缝，裂缝宽度未超限，此外底板以及翼缘板局部混凝土剥落，剥落处箍筋存在钢筋锈蚀，剥落面积小于5%。手搓混凝土表面，有砂粒滚动的摩擦感觉，砂粒较少。

基于以上桥梁主要检测结果，T梁截面损伤综合评定标度R=1.65，截面折减系数取0.99，部分保护层脱落，箍筋存在锈蚀，钢筋截面折减对应评定标度2，钢筋截面折减系数取值0.97，详细评定结果列于表5。

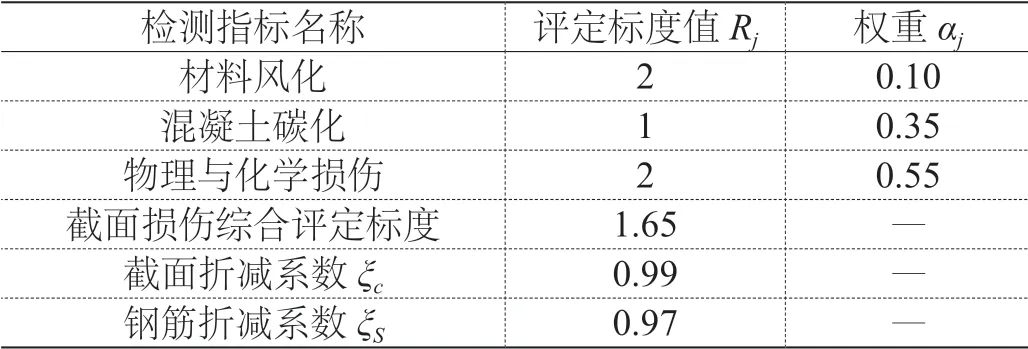
表5 截面折减系数和钢筋截面折减系数取值

依据折减系数ξc和ξS对截面刚度矩阵的影响系数表建立刚度退化的有限元分析模型[5]。由于Midas Civil分析模型中梁单元不计入钢筋对刚度的影响，可将钢筋截面换算成等效截面，按照影响系数表调整参数进行分析计算，对于实体模型，可在Midas FEA分析模型中将钢筋单元按照线单元输入计算。莲溪大桥梁单元计算模型见图1，实体单元计算模型见图2。

图1 Midas Civil梁单元分析模型

图2 Midas FEA实体单元分析模型

4 结果分析

根据各截面折减系数下的退化模型分析，得到不同折减系数下各阶振型及理论特征值，如表6、表7所示，桥梁截面折减系数ξc对应特征值关系图及折减系数对特征值影响程度图见图3和图4所示，钢筋截面折减系数ξS对应特征值关系图及折减系数对特征值影响程度图见图5和图6所示。同时对莲溪大桥第11跨进行动力特性参数测试，判断桥梁结构的固有振动特性，结合该跨混凝土材料的风化、碳化、物理与化学损伤以及钢筋截面折减确定退化模型1阶竖弯频率，实测1阶竖弯值和退化模型1阶竖弯见表8。

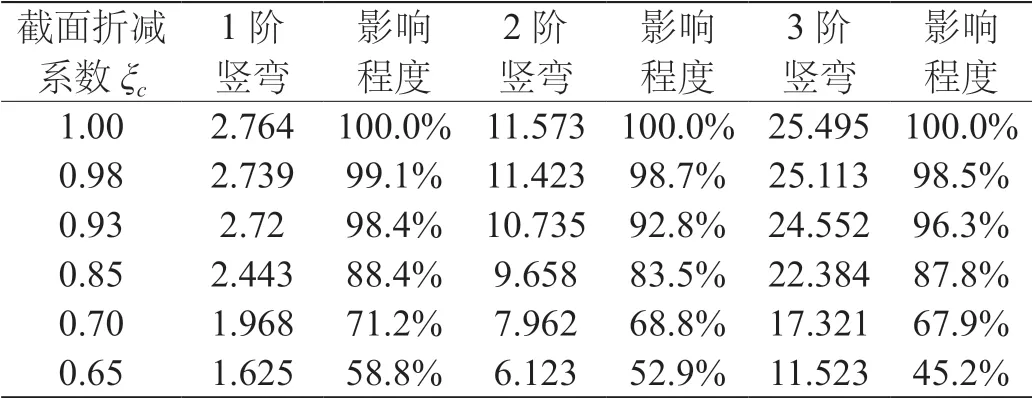
表6 桥梁截面折减系数对特征值影响结果 /Hz

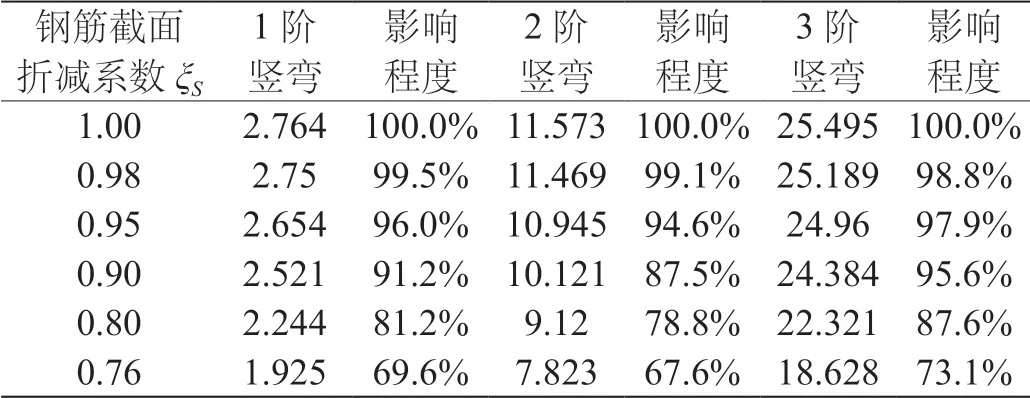
表7 钢筋截面折减系数对特征值影响结果 /Hz

图3 桥梁截面折减系数对应特征值关系图

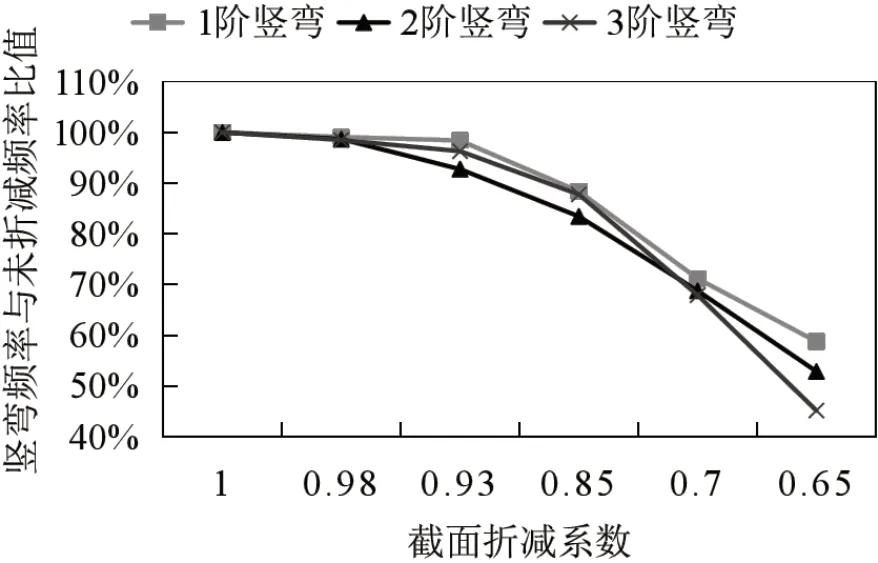
图4 桥梁截面折减系数对特征值影响程度图

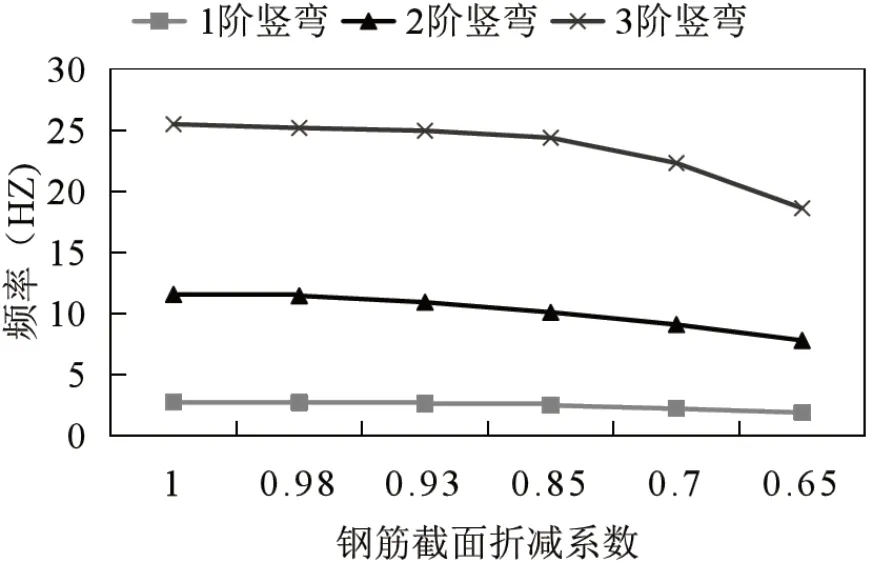
图5 钢筋截面折减系数对应特征值关系图

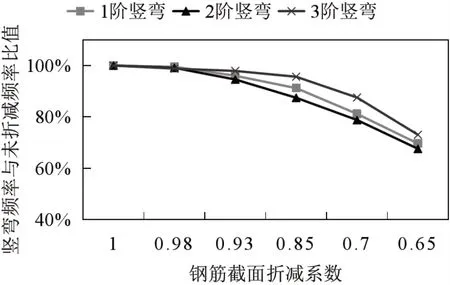
图6 钢筋截面折减系数对特征值影响程度图

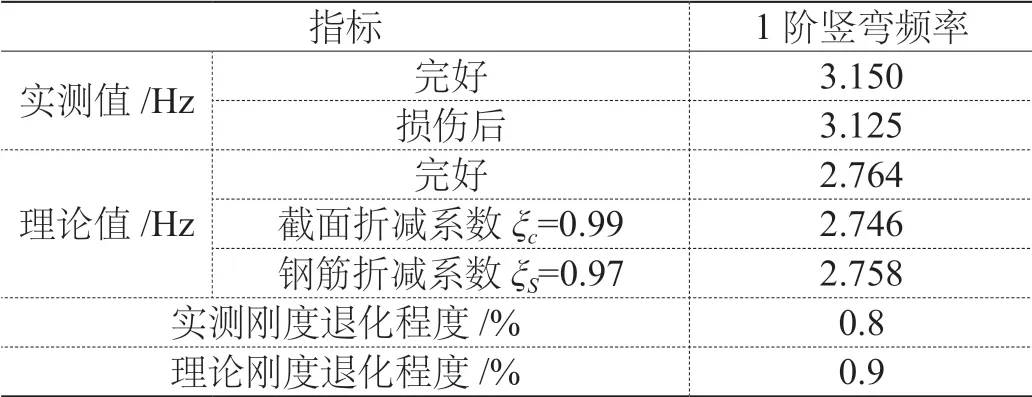
表8 实测1阶竖弯值和退化模型1阶竖弯对比

5 结论

通过对配筋混凝土桥梁截面折减系数ξc和配筋混凝土钢筋截面折减系数ξS对混凝土及钢筋截面折减及桥梁结构刚度退化分析，得出以下结论：

（1）随着桥梁截面折减系数ξc的降低，桥梁结构的竖弯频率呈非线性降低趋势；折减系数一定时，阶数越高，刚度退化越显著；对于钢筋截面折减系数ξS，竖弯频率呈非线性降低趋势明显小于桥梁截面折减系数，阶数越高，刚度退化越慢；说明桥梁截面折减系数ξc对桥梁整体刚度（尤其是高阶频率）退化贡献更大。

（2）莲溪大桥第11跨简支梁实测1阶竖弯频率为3.125 Hz，结合该跨混凝土材料的风化、碳化、物理与化学损伤以及钢筋截面折减引入刚度退化模型进行分析，结构刚度退化约0.8%，与理论分析基本一致，表明该退化模型对于该类混凝土简支桥梁具有实用性。