基于投影法的道路路线方案设计

赵 颖

（中国公路工程咨询集团有限公司,北京 100089）

0 引言

目前，学术界对多指标决策与评价的研究已经取得不少成果，所提出的全新投影决策方法也在经济效益综合评价领域得到成功应用。该投影决策方法算法简单，结果准确可靠，具有推广应用价值。该文正是依托具体道路工程，应用投影法展开路线方案比选及设计探讨，以期为全新投影决策方法在道路路线设计中的应用提供借鉴。

1 工程背景

某道路为国道改建工程，起讫桩号K820+200～K830+510，路线长10.31 km，为双向四车道一级公路，特殊路段则按双向六车道设计；一般路段和地形复杂路段设计车速分别为80 km/h和60 km/h。一般路段整体式路基和分离式路基分别宽25.5 m、12.75 m，特殊段路基宽33 m。原公路路面狭窄，弯急坡陡，平纵面线形指标较差，很难满足设计车速要求，再加上车辆普遍超载超限，安全隐患十分突出。为此，在改建前，必须展开路线方案的合理设计。

2 指标选取及模型构建

2.1 指标选取

结合《公路路线设计规范》及相关规定，道路路线评价指标体系中所包含的指标可以分成优秀、良好、一般、合格、较差5个等级，各项指标取值位于[85,100]之间时为优秀，位于[75,85)之间时为良好，位于[65,75)之间时为一般，位于[50,65)之间时为合格，低于50为较差[1]。

在确定各指标评价量值时，工程投资为固定性指标，其余指标的评价量值均通过专家打分的方式获得[2]。限于篇幅，仅列出其中占地面积和土石方量两个子指标的专家打分情况及分级标准，见表1和表2。

表1 土石方量子指标的打分情况及分级标准

表2 占地面积子指标的打分情况及分级标准

2.2 模型构建

为便于模型构建，将该道路工程路线方案集表示为A={A1,A2,A3, …An}，评价指标集表示为G={G1,G2,G3, …Gm}，方案Ai指标Gj的属性值为yij，其中i=1,2,3,…n，j=1,2,3,…m，指标集合通过Y=(yij)n×m矩阵表示，如下：

将以上述矩阵作为方案集A对指标集G的属性矩阵，也就是多目标决策矩阵。

道路路线方案设计所涉及的指标分为效益型、成本型、固定型及区间型，其中效益型指标的属性值往往越大越好，如路网功能，此类指标为专家打分的主要指标；固定型指标通常存在一个最佳取值，如技术标准；区间型指标属性值必须位于一定的范围区间内，如土石方量、占地面积等。不同类型的评价指标量纲不同，为消除量纲不同所造成的非公度性和不可比性，必须将决策矩阵中量纲不同的目标属性值进行无量纲化处理[3]，过程如下：

效益型、成本型、固定型及区间型指标无量纲处理公式如下：

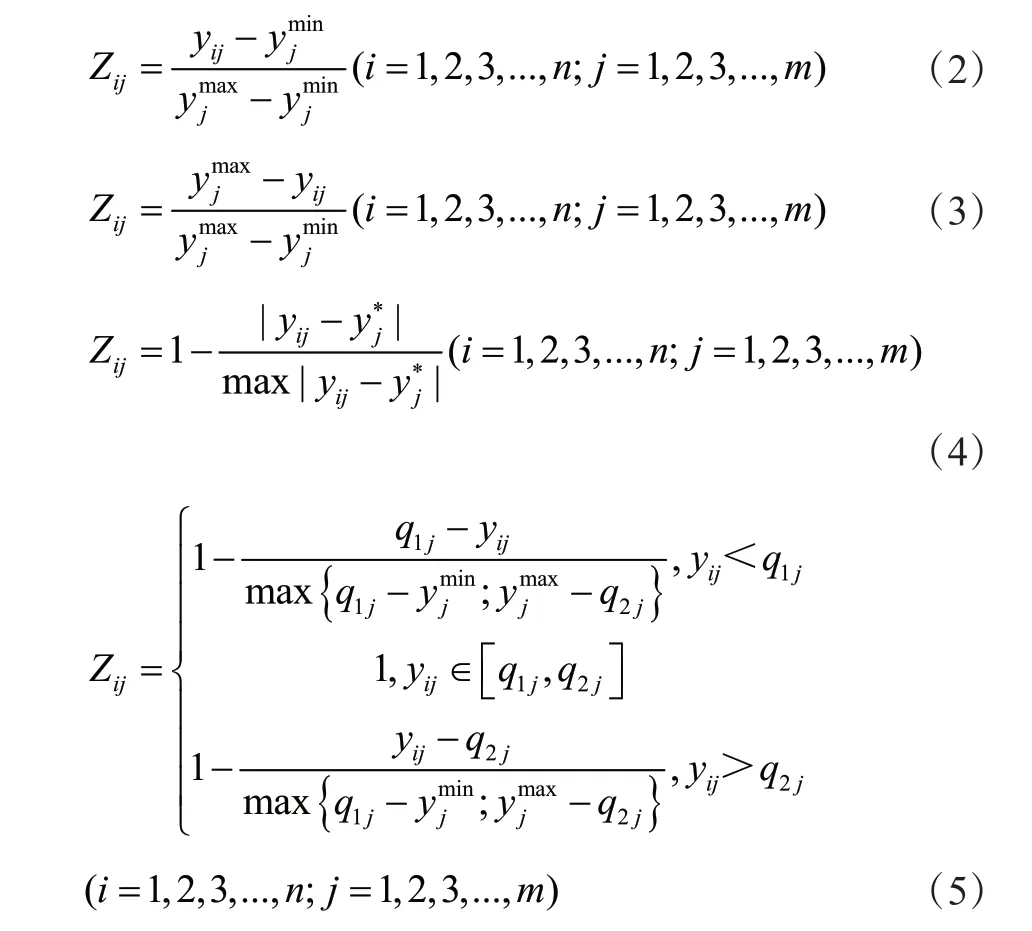
式中，Zij——各类指标的无量纲量；——Gj指标的最大值；——Gj指标的最小值；——固定型指标Gj的稳定值；[q1j,q2j]——区间型指标的稳定区间。

将无量纲处理后的决策矩阵记为Z=(Zij)n×m，见式（6），Zij∈[0,1]，且取值越大越好。

理想方案A*主要由理想属性值构成，经无量纲处理后理想方案评价指标中权向量W=(W1,W2,W3, …,Wn)，其中W的确定方法包括客观赋值法和主观赋值法两类，为确保评价结果的客观准确，该文采用客观赋值法。公式如下：

依托上式，为增强投影决策方法含义的明确性及决策结果的准确性，并充分考虑约束条件，将所得出的权向量单位化。公式如下：

2.3 最优方案的确定

基于以上分析，构建加权规范化最优决策矩阵：

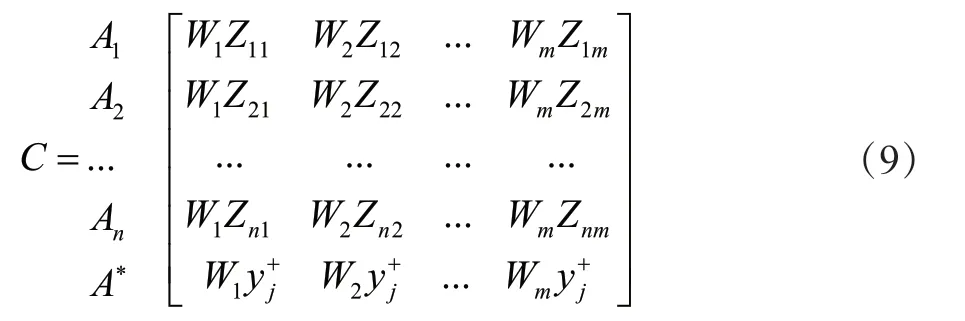
若将各方案指标属性值视为1个矢量，可以绘制出各决策方案Ai和理想方案A*的关系。决策方案Ai和理想方案A*间夹角的余弦值按照下式确定：

结合相关理论，决策方案Ai的模可表示如下：

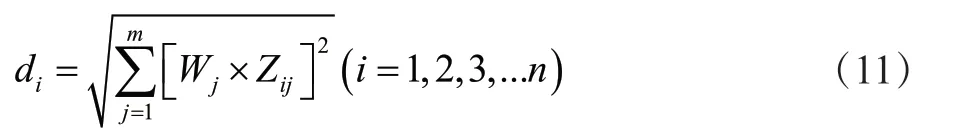
决策方案Ai和理想方案A*间夹角的余弦值体现的是两个值方向的一致性，但无法反映出各方案模的大小；而决策方案Ai的模能弥补夹角余弦值的不足，但无法反映决策方案和理想方案的变动方向。为保证决策结果的合理准确，必须在量化计算决策方案Ai和理想方案A*间夹角的余弦值外，还应充分考虑各方案模的大小，较好地得到决策方案Ai和理想方案A*间的逼近程度。令决策方案Ai在理想方案A*上的投影为Di，表示如下：

式中Di∈(0,1]，且其取值越大越好。考虑到加权向量符合单位化约束条件，所以理想方案A*的投影可进一步表示为：

此处所采取的投影法的实质是，将决策方案Ai在理想方案A*上的投影值视为评价道路路线方案优劣的主要依据，且投影值越大，意味着路线方案也越接近理想方案。

3 路线方案比较

结合该道路工程建设实际及设计思路，提出4个路线方案，相关数据可以写出该道路路线方案设计多目标决策矩阵，如下：

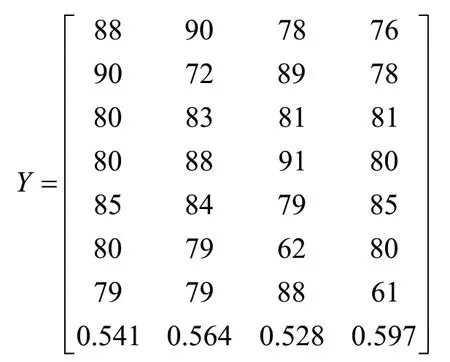
对该道路工程路线方案进行评价的指标体系中，投资额为固定型指标，其余均可视为效益型指标，属性值均通过专家打分方式获取。根据式（2）和（4）进行相应指标无量纲处理，最终得出的决策矩阵列示如下：

通过式（7）求各指数，具体如下：

单位化处理向量后得出权向量：

应用式（9）进一步得出加权规范化最优决策矩阵：

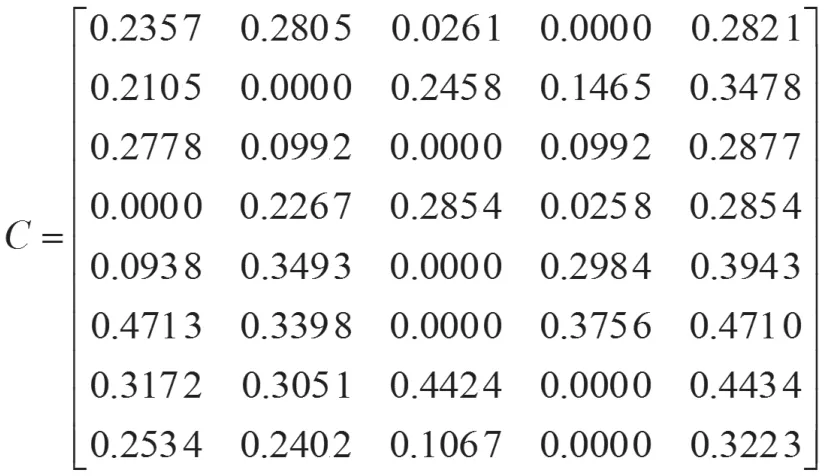
应用式（10）～（12），依次求出以上4个决策方案的模di、决策方案Ai和理想方案A*间夹角的余弦值ri、决策方案Ai在理想方案A*上的投影Di值，结果汇总至表3。根据表中结果，各决策方案在理想方案上的投影值从大至小排序为：D1＞D2＞D3＞D4，应以方案1为最优的路线设计方案。

表3 决策方案相关参数计算结果

4 结论

综上所述，依托投影法构建起的道路路线方案评价模型能较好解决路线方案比选所面临的多指标、多属性等问题，通过对各决策方案在理想方案上投影值大小的计算，更加可靠准确地体现各决策方案和理想方案间的逼近与吻合程度，最终得出较为可靠的路线方案。在采用该文所提出的路线方案后，该国道改建工程路线布设合理，在路线布置过程中最大限度地避开了不良地质，也大大降低了征地拆迁规模及对沿线居民、环境的不利影响，路线设计的科学性、合理性及技术性水平明显提升。