余弦编码复用高空间分辨率关联成像研究

李能菲,孙宇松,黄见

(1安徽职业技术学院机电工程学院,安徽 合肥 230011;2中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院大气光学重点实验室,安徽 合肥 230031;3中国科学技术大学研究生院科学岛分院,安徽 合肥 230026;4先进激光技术安徽省实验室,安徽 合肥 230031)

0 引言

关联成像是一种新型的计算成像技术,其与传统面阵成像的区别在于关联成像的成像器件为无空间分辨率能力的点探测器,由于点探测器相对于面阵CCD/CMOS探测器具有光谱选择范围大、量子效率高等优势,使得关联成像在现有面阵成像无法工作的非可见光波段具有潜在的成像优势,近年来成为光学、电子学和计算机科学等众多交叉学科的研究热点。关联成像起源于纠缠光子光源[1],因此部分研究人员也将关联成像称为量子成像。后续的研究表明经典光源[2−4]也可以实现关联成像。在传统的关联成像系统中,光源发出的光被分成两路,一路称为参考光路,另一路称为探测光路。参考光路的光不与成像物体接触,直接被面阵探测器接收;探测光路的光与成像物体相互作用后被一点探测器收集,联合参考光路记录的光强分布与探测光路记录的光强经关联运算可重建出物体图像。研究发现,使用空间光调制器产生光强空间分布预知的调制光源可以省略掉参考光路[5],大大简化了关联成像系统,推动了关联成像进一步向实用化方向发展。目前,关联成像在多光谱成像[6−8]、红外成像[9]、太赫兹成像[10,11]、气体检测[12]、偏振成像[13]、三维成像[14−16]以及目标跟踪[17−19]等领域都展现了其广阔的应用前景。

不同于传统面阵成像,关联成像通过一系列被掩膜图案调制的光源照射场景,无空间分辨能力的点探测器记录相应的光强,通过联合光强与掩膜图案做关联运算来重建场景图像,关联成像的这种成像机制决定了其是一种以牺牲时间分辨率换取空间分辨率的成像技术,成像空间分辨率越高,所需的调制散斑越多,使得采样时间长、成像效率低。因此,如何在保持较高成像质量的基础上、在低采样数下获取更高的空间分辨率与帧频成为关联成像走向实际应用必须突破的关键科学问题。文献[7,8]和文献[20]采用相互正交的随机编码复用分别实现了多光谱关联成像、多物体成像与加密,由于编码信息空间分布是随机的,使得在图像重构时需利用压缩感知优化算法来对随机编码对应的欠定方程组进行求解,导致图像复原时间消耗大大增加。

本文提出了一种余弦编码复用高空间分辨率关联成像技术,通过构造多个低空间分辨率的余弦编码散斑复用为高空间分辨率调制散斑,对成像物体进行调制照明,单像素探测器接收被调制物体信号,由迭代算法复原出成像目标低空间分辨率的混叠图像;鉴于编码信息所特有的确定性频谱结构,利用数字图像处理解码重构出多个低空间分辨率物体图像,进而拼接为高空间分辨率目标图像。理论介绍了余弦编码复用高空间分辨率关联成像技术的实现方法,数值仿真验证了此方法的有效性。

1 传统关联成像方法

图1为关联成像系统示意图,投影器件产生变化的调制光源Si(x,y),对成像物体O(x,y)进行调制照明,调制照明光源与成像物体相互作用产生的后向散射信号被光学透镜汇聚后,由无空间分辨能力的单像素探测器收集,从而实现光电转换,数据采集单元同步采集相应的电信号,并存储在计算机中供后续图像复原使用。设与调制信号Si(x,y)对应的探测光强为Ii,则Ii可表示为

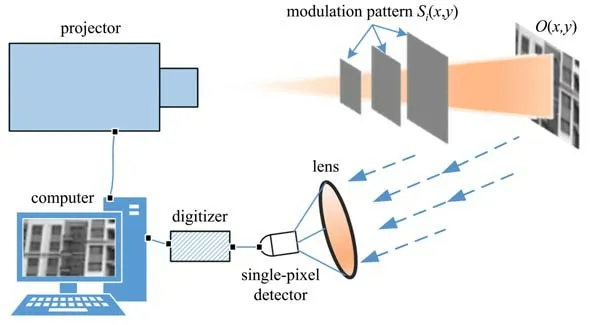
图1 关联成像系统示意图Fig.1 Schematic diagram of the ghost imaging system

式中:L为调制次数。对于空间分辨率为N×M的物体成像,一般情况下全采样时L=NM。对(1)式求解常用的方法是迭代算法,即

传统关联成像对空间分辨率为N×M的物体关联成像时,全采样需要N×M个调制散斑,散斑数据量随着空间分辨率提高呈平方关系增加。如,对128×128分辨率物体成像需要调制散斑数为16384,假设调制频率为20 kHz,则全采样一幅图像的时间至少为0.8 s;当对256×256分辨率物体成像,需要调制散斑数为65536,在同样的调制频率下,则全采样一幅图像的时间至少为3.2 s,成像帧频大幅降低。可以看出,成像物体的空间分辨率越高,需要的调制散斑越多,相对应采样次数就越多,进而不可避免地增加了成像时间。

2 余弦编码复用高空间分辨率关联成像方法

本研究提出采用多个余弦编码的低空间分辨率复用调制散斑来实现N×M高空间分辨率的关联成像。为便于表述,这里假设将N×M空间分辨率的物体等分为2部分,即P1:(1:N,1:N)和P2:(1:N,N+1:M),其中M=2N。通过获取2个(1:N,1:N)低空间分辨率的图像来实现对N×M高空间分辨率物体的成像。构造两个N×N二维余弦结构编码矩阵,分别对应被成像物体的两个部分,记为EP1和EP2,即

式中:a为编码矩阵的对比度,b为编码矩阵的偏置,fx1和fy1为编码矩阵EP1的频率,fx2和fy2为编码矩阵EP2的频率,φ0为编码矩阵的初始相位。将余弦编码矩阵和基于Hadamard基生成的图案Si(x,y)相融合,可生成两个空间分辨率大小为N×N的调制散斑EP1·Si(x,y)和EP2·Si(x,y),符号·表示点乘运算。将这两个调制散斑横向排列,可构成空间分辨率为N×M的调制散斑,该高空间分辨率的调制散斑同时对成像物体的P1和P2部分调制照明,单像素探测器收集空间分辨率为N×M物体的反射或者透射信号Ui,可表示为

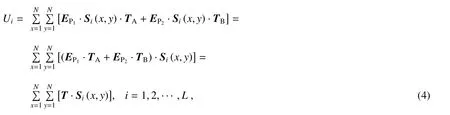
式中:TA和TB分别对应成像物体空间分辨率大小为N×N的P1部分和P2部分;T表示成像物体的混叠图像,辨率为N×N,数值上T=EP1·TA+EP2·TB。鉴于Si(x,y)为基于Hadamard基的正交散斑,可通过线性迭代运算对(4)式中T进行求解,即

在获取T后,如何从分辨率为N×N的混叠图像T中解调重构出TA和TB是本技术的核心。由于余弦编码矩阵EP1和EP2具有特定的频谱特性,可以利用傅里叶变换理论来处理。对混叠图像T做傅里叶变换,将其从空间域转换到傅里叶频域,即

式中符号F表示对图像做二维傅里叶变换。将欧拉公式cosx=(eix+e−ix)/2代入(6)式,由傅里叶移位定理可推导出

式中:FTA和FTB分别为低空间分辨率图像TA和TB对应的频谱,fx和fy表示频谱坐标。由(7)式可以看出,在频域中由于TA和TB的编码频率组合(fxi,fyi)不同,TA和TB的频谱信息被频移到混叠图像频谱的不同高频区域。因此,在混叠图像频谱图中会出现两对频点(对称性),对应图像TA和TB频谱信息中的最大值。首先将混叠图像频谱中一对频点平移到傅里叶域的中心,同时保持另外一对频点信息位置不变,然后用低通滤波器适当地提取平移后的频谱信息,最后对提取到的频谱信息做二维傅里叶逆变换处理,可以得到TA和TB,即

式中:符号F−1表示对图像做二维傅里叶逆变换,RA和RB分别为平移重组后TA和TB的频谱图,X表示低通滤波器,最终按照调制照明时散斑的横向排列,将TA和TB融合为一空间分辨率为N×M的目标图像。

余弦编码复用高空间分辨率关联成像的基本流程如图2所示,余弦编码矩阵与Hadamard基图案复用来产生调制信息,按照与成像物体(图2中object)空间结构相同的方向对调制信息进行排列,构成高空间分辨率的调制照明散斑(图2中的MP);照明散斑对成像物体进行调制,单像素探测器收集调制照明光与物体相互作用后的总能量,然后利用线性迭代算法复原出物体的混叠图像T;对T做二维傅里叶变换,得到混叠图像的频谱图F,对频谱进行重组,从而获得不同编码信息对应的低空间分辨率物体频谱信息(图2中RA和RB),利用低通滤波器(图2中X)提取合适的频谱信息,再进行傅里叶逆变换,从而实现对低空间分辨率物体图像的重构(图2中TA和TB),最后按照调制照明散斑排列的顺序获得高空间分辨率物体图像(图2中RI)。

图2 余弦编码复用高分辨率关联成像的基本流程Fig.2 Flow chart of the cosine encoded multiplexing high-resolution ghost imaging

3 仿真验证

上节理论分析了余弦编码复用高空间分辨率关联成像方法,本节将通过数值仿真来验证此方法的有效性。设成像物体的空间分辨率为256×512,按照所提方法可以将其分为两个空间分辨率为256×256的子图像来处理,其中P1对应物体的(1:256,1:256)部分,P2对应物体的(1:256,257:512)部分。因此,Hadamard基图案和余弦编码矩阵EP1与EP2的维数设置为256×256。其中,(3)式中编码矩阵的对比度a和偏置b均设置为0.5,fx1=0,fy1=128,fx2=128,fy2=0,生成的编码矩阵及其对应的傅里叶频谱如图3所示。可以看出编码矩阵EP1的频谱在空间坐标(129,1)位置上有一处明显的冲激点,编码矩阵EP2的频谱在空间坐标(1,129)位置上具有明显冲激点,这种特征有利于后续的高空间分辨率图像解码重构。

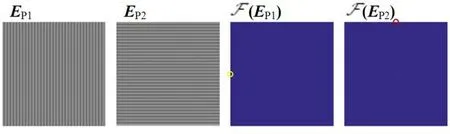
图3 余弦编码矩阵及其傅里叶频谱。EP1与EP2为余弦编码空间表现形式;F(EP1)和F(EP2)为编码矩阵的傅里叶频谱Fig.3 Cosine encoded matrices and their Fourier spectra.EP1 and EP2 demonstrate the spatial representations of the cosine encoded matrices.F(EP1)and F(EP2)demonstrate the Fourier spectra of the employed cosine encoded matrices

本方法在应用傅里叶逆变换复原低空间分辨率子图像过程中,选取的频谱范围对重构的图像质量影响较大。这里选用理想低通滤波器来提取子图像的频谱,理想低通滤波器X(fx,fy)定义为

式中:R(fx,fy)为傅里叶域中空间坐标(fx,fy)到中心原点的距离;R0为滤波半径,滤波半径的大小表征了物体频谱信息对应的截至频率。为定量评估重构图像的质量,分别采用均方差(MSE,EMS)和结构相似性指数[21](SSIM,MSSI)来对重构图像进行评估,分别表示为

式中:c(x,y)为空间位置(x,y)上的灰度值;o(x,y)表示仿真使用的原始图像空间位置(x,y)上的灰度值,MSE大小反应了复原图像与原始图像之间的误差,其值越小表示复原图像质量越高,越接近原始图像;µc和µo为重建图像和原始图像的像素点均值;σc和σo分别是重建图像和原始图像的标准差;σco是协方差;C1和C2是稳定弱分母常数,C1=(K1L)2,C2=(K2L)2,一般情况下K1=0.01,K2=0.03,L=255。SSIM衡量图片的失真程度,当两张图像一模一样时,SSIM的值等于1。

本文方法在实现对空间分辨率为256×512的物体成像时,全采样所需的余弦编码复用调制散斑数量为65536(等于256×256),65536个复用的调制散斑与空间分辨率为256×512的成像物体[如图4(a)]相互作用后产生对应的65536个强度值,联合调制散斑和强度值,利用线性迭代算法复原出成像物体的混叠图像,如图4(b)所示。混叠图像的空间分辨率为256×256,混叠图像在数学上是对高空间分辨率物体图像抽样所形成的低分辨率的图像,其融合了编码信息与空间强度信息。对混叠图像做傅里叶变换可得其对应的傅里叶频谱,如图4(c)。为更直观地展示,将低频信息平移到图像的中心位置,即低频信息在频谱图像的中间位置,高频信息在频谱图像的边缘位置。鉴于所构造编码矩阵具有的特定频谱结构,低空间分辨率图像的频谱被频移到混叠图像傅里叶域的高频区域,即图4(c)空间坐标(129,1)和(129,256)以及(1,129)和(256,129)附近区域,将低空间分辨率对应图像的频谱平移到频谱图像的中心位置,可得到两个低空间分辨率图像的频谱图,如图4(d)、(e)所示。

图4成像物体、复原的混叠图像及其傅里叶频谱。(a)空间分辨率为256×512成像物体图像;(b)复原的256×256成像物体的混叠图像;(c)混叠图像的傅里叶频谱;(d),(e)为对(c)频移后对应低空间分辨率子图像的频谱图Fig.4 Picture of the imaged object,restored mixed image and its Fourier spectrum.(a)Image of the object with 256×512 resolution;(b)Reconstructed mixed image of the object with 256×256 resolution;(b)Fourier spectrum of the reconstructed mixed image;(d),(e)Fourier spectrum of the low spatial resolution image obtained through frequency shift from(c)

图5 为余弦编码复用高空间分辨率关联成像仿真实验结果。通过使用理想低通滤波器来分别提取图4(d)、(e)低频信息,然后应用傅里叶逆变换来复原相应的低空间分辨率物体图像,最后将复原的两个低空间分辨率图像合成为一个高空间分辨率图像。图5(a)∼(h)展示了滤波半径分别为12、24、32、40、48、56、64、72 pixel时复原的结果。当滤波半径较小时提取的频谱信息较少,复原的图像比较模糊;随着滤波半径的逐渐增大,提取的频谱信息增大,复原图像的MSE逐渐减小,误差变小,SSIM逐渐增加,即复原的图像和原图的相似度提高;但是当滤波半径大于56时[图5(g)和(h)],可能是选取频谱出现了混叠,导致MSE和SSIM逐渐变差。总体上,通过选择合适的滤波半径,余弦编码复用能够高效地实现对高空间分辨率物体成像。在高空间分辨率图像复原时,本研究分别使用了迭代算法和数字图像处理的相关方法,使得时间消耗大大降低;在主频为2.3 GHz、i7-10875H处理器以及16 G内存计算机上,应用MATLAB R2015b实现256×512分辨率成像复原的时间消耗约为21.13 s,去除迭代算法复原混叠图像的时间消耗,仅从混叠图像中解码重构两个低空间分辨率图像时间消耗约为0.82 s。

图5 利用理想低通滤波器复原的结果,滤波半径分别为:(a)12 pixel;(b)24 pixel;(c)32 pixel;(d)40 pixel;(e)48 pixel;(f)56 pixel;(g)64 pixel;(h)72 pixelFig.5 Recovered results with ideal low-pass filters.The filter radius are(a)12 pixel;(b)24 pixel;(c)32 pixel;(d)40 pixel;(e)48 pixel;(f)56 pixel;(g)64 pixel;(h)72 pixel,respectively

利用多个低空间分辨率的余弦编码散斑复用为高空间分辨率调制散斑对物体调制成像时,调制散斑数量与低空间分辨率的调制散斑相同,能够大幅降低调制散斑数据,以提高高空间分辨率关联成像的成像效率。利用本方法对成像物体划分的块数增多,频谱尺寸减小,低通滤波器的半径受到进一步限制,复原的高空间分辨率图像质量会有一定程度的降低。下面将256×256空间分辨率的物体分别等分为2部分和4部分来处理,并定量计算重构图像的质量(SSIM和MSE)。结果如图6所示,其中图6(a)为仿真使用的空间分辨率为256×256的测试图像。当将256×256分辨率物体等分为4部分时,每部分的空间分辨率为128×128,此时全采样所需的散斑数量为16384,为了防止频谱重叠,最大的滤波半径为32 pixel。图6(b)∼(e)分别是滤波半径为8、16、24、32 pixel时的成像结果,可以看出随着滤波半径的增加,复用的图像质量逐渐增加,最大的SSIM为0.7112,最小的MSE为0.0032。相应地,当将256×256分辨率物体等分为2部分时,每部分的空间分辨率为128×256,此时全采样所需的散斑数量为32768,为了防止频谱重叠,此时最大的滤波半径为64 pixel。图6(f)∼(j)分别为滤波半径为32、40、48、56、64 pixel时的成像结果,同样可以看出,随着滤波半径的增加,复用的图像质量逐渐增加,即使在滤波半径为32 pixel时,复原图像的SSIM和MSE分别达到了0.7698和0.0025,比等分为4部分时的高。仿真表明,等分数量的增加虽然降低了采样次数,但也降低了高空间分辨率成像质量,因此在应用本研究所提出方法时需兼顾成像分辨率(划分的块数)和成像质量。

图6 应用所提出方法将成像物体等分为4份和2份时的成像对比。(a)仿真使用的测试图像;(b)∼(e)将成像物体等分为4份,滤波半径分别为8、16、24、32 pixel时利用理想低通滤波器复原的结果;(f)∼(j)将成像物体等分为2份,滤波半径分别为32、40、48、56、64 pixel时利用理想低通滤波器复原的结果Fig.6 Imaging comparison when the imaging object is equally divided into 4 and 2 parts by using the proposed method.(a)Testing imaging object;(b)∼(e)Recovered results using ideal low-pass filters with the filter radius at 8,16,24 and 32 pixel respectively when the imaging object is equally divided into 4 parts;(f)∼(j)Recovered results with the filter radius at 32,40,48,56 and 64 pixel respectively using ideal low-pass filters when the imaging object is equally divided into 2 parts

4 讨论与结论

关联成像的机理决定了其成像效率和空间分辨率相互矛盾。横向空间分辨率越高则所需的调制信息越多,在调制频率一定的情况下,使得采集时间过长,无法满足实际需求。本研究提出了一种余弦编码复用高空间分辨率关联成像技术。通过构造多个低空间分辨率的余弦编码散斑复用为高空间分辨率调制散斑对成像物体进行调制照明,联合调制信号以及调制信号与成像物体相互作用后的强度值,利用线性迭代算法复原出成像场景的混叠图像;应用傅里叶变换将混叠图像从空间域转换到频域,通过频域中的频移操作分别获取低空间分辨率物体频谱,然后利用理想低通滤波器来选取合适频谱以重构低空间分辨率物体图像,最后按照低空间分辨率调制散斑的排列次序合成高空间分辨率物体图像。数值仿真验证了所提出方法的有效性,所实现的余弦编码复用高空间分辨率关联成像大幅降低了调制散斑数量,减少了在线采样时间,同时在低空间分辨率图像重构时规避了传统优化算法,进一步降低了图像重构的时间消耗,在生物医学等要求高空间分辨率且对时间苛刻的领域具有一定的应用价值。