利用Mallows-φ模型的不完整序数偏好预测
2022-12-06付晓东刘利军
孙 凯,付晓东,2,刘 骊,刘利军
1(昆明理工大学 信息工程与自动化学院,昆明 650500)
2(昆明理工大学 云南省计算机技术应用重点实验室,昆明 650500)
1 引 言
用户在与商品、服务等对象产生交互后,可以基于其自身的评价准则以及对评价对象的主观感受对其做出相应的评价[1].此类评价也被称为用户对评价对象的偏好,它反映了用户对评价对象的喜好和满意程度.用户偏好在社会选择[2]、在线服务信誉度量[3]、推荐系统[4]等领域中发挥着重要的作用:社会选择通过对单个用户偏好进行聚合,选择出符合群体利益的最优评价对象;在线服务信誉度量基于用户偏好对在线服务的信誉进行评价,评价结果可以辅助用户更好地进行在线服务选择;推荐系统中基于用户的偏好对商品和服务等进行推荐,使得推荐结果更加符合用户的个性化需求,提高用户的满意度.用户偏好主要表现为基于数值评分的基数偏好以及序数偏好两种形式[5].由于不同用户的评价准则不一致,导致不同用户的基数偏好和文本型偏好不可公度[6].序数偏好是指用户根据自身对不同评价对象的偏好关系形成的排名结果,可有效的解决了评价准则不一致的问题[6].更加广泛和实用的用户序数偏好通常采用成对比较的形式,成对比较可被视为序数偏好的基本构成单位[7].如某个用户认为评价对象s1优于s2、评价对象s3优于s4等.这种形式的偏好在网络搜索、产品比较、广告点击等选择场景中十分普遍.此外,成对比较也可以用于对完整排名、部分排名、Top-k等多种形式的序数偏好建模[8].
不完整序数偏好是指用户提供的成对比较偏好无法构成对所有评价对象的完整排名,即用户没有对所有的任意两个评价对象进行比较.获取用户的完整序数偏好存在以下几个方面的困难:首先,由于评价对象的数量众多,用户不可能与每个评价对象都有交互的经验,因此也不可能对所有评价对象进行评价;其次,要求对评价对象进行完整排名会导致不必要的认知和沟通需求[9];最后,用户可能会出于对自身隐私的考虑,不愿意提供其全部的已知偏好.因此,通常只能获得用户的不完整序数偏好.基于不完整序数偏好进行社会选择、在线服务信誉度量、产品推荐等决策时,由于缺失偏好的影响,难以得到符合用户真实偏好的决策结果,进而使得决策结果缺乏有效性.
当用户序数偏好不完整时主要有以下解决方法:直接基于已知偏好进行评价,忽略未知偏好对评价结果的影响,难以保证评价结果的有效性[10];向用户获取足够多的缺失偏好[11],然后进行决策.由于通信和查询的复杂性,使得评价成本大大增加;另一种解决方法是使用排名概率模型对不完整偏好进行建模,然而相关工作[12]对偏好的类别进行了限制,只能用于Top-k等形式的偏好,不能对成对比较形式的序数偏好进行处理.为解决用户偏好不完整场景下对评价对象进行评价时存在的问题,本文采用Mallows-φ概率模型对成对比较形式的不完整序数偏好进行预测,模型反映了用户对评价对象进行成对比较和排名的过程,可以较好地对成对比较形式的偏好进行建模.首先,使用不完整成对比较序数偏好训练Mallows-φ模型;然后基于训练得到的模型对不完整偏好进行预测.该预测过程通过对用户可能的完整偏好的概率进行分析来做出决策,使得预测结果更加准确.通过在合成数据和真实数据上进行实验,验证了使用该模型进行成对比较序数偏好预测的有效性.
2 相关工作
近年来,国内外学者展开了一系列基于用户偏好对商品、服务等对象进行评价的研究.用户偏好主要分为基数偏好、文本型偏好和序数偏好[13].
基于基数偏好(评分)的评价方法主要有平均值法和累加法[14].不完整基数偏好的预测方法主要有协同过滤方法[15,16]、加权平均值和中心加权平均值统计方法[17].其中协同过滤方法利用相似用户之间具有相似偏好的性质,来发现用户对评价对象的潜在偏好;加权平均值法根据当前用户与相邻用户之间的相似性对当前用户的缺失偏好进行预测;中心加权平均值法根据不同用户的评分值、加权评分值与该用户平均评分之间的差值对该用户的缺失偏好进行预测.由于生活经验、自身习惯等的影响,用户的评价准则通常不一致.例如,有些用户倾向于给出较高的评分,有些用户倾向于给出较低的评分,导致表现相同的评价对象得到不同的评分.因此,不同用户对同一评价对象的评分事实上不可比较[6],基于所有用户评分进行评价的结果缺乏客观性.然而,上述对不完整评分偏好进行处理的方法都假设不同用户具有相同的评价准则,未考虑用户评分的不可比较性,使得评价结果难以真实反映不同对象之间的优劣关系.
基于文本偏好,文献[18]提出了一种基于评论语言特征和支持回归向量的在线评价排名方法,从而帮助用户更好地了解评论的质量;文献[19]针对文本评论的各种评价因素进行量化评价,提出一种利用灰色评估理论分析用户情感满意度的评价方法;文献[20]通过分析每个评价对象的已知文本评价,识别出其所拥有的特性并给出相对应的评分,进而对评价对象进行评价排名.在偏好不完整时,文献[21]提出了HFT(hidden factors as topics)模型,通过综合考虑文本评价数据与数值型评分数据,最终可更准确地对缺失的评分进行预测.然而,此类对不完整文本偏好进行处理的方法同样假设不同用户具有相同的评价准则.
基于序数偏好进行评价时,由于考虑了用户对不同评价对象之间的偏好关系,因此解决了不同用户的评价准则不一致的问题[6].当序数偏好完整时,即包含所有评价对象的成对比较,此时的用户偏好相当于对所有评价对象的一个完整排名,可以利用社会选择方法对所有用户偏好进行聚合,得出评价排名.考虑到序数偏好不完整,文献[22]基于不完整偏好提出了一种基于支配关系的计算模型,其通过多数准则确定评价对象最终的排名.然而,当只有极少数的人对某两个评价对象进行比较时,难以确定这两个评价对象间的优劣关系,因此直接基于不完整偏好构建的有向无环图缺乏代表性和准确性;通过偏好抽取[11]的策略,可以减少缺失偏好的影响,即通过向用户询问缺失的偏好可以提高偏好的完整性.然而为了得到较高质量的决策结果,需要向用户进行足够多的询问,通信和查询的复杂性增加了评价成本,因此偏好抽取方法往往只适用于选择单一胜者的场景;另一种减少缺失偏好的影响的方法是使用排名的概率模型对不完整偏好的各种完整补全的概率进行精细的分析,进而对不完整偏好做出预测.众多的研究工作使用统计、心理计量学和计量经济学的排名模型[12]来建模用户的偏好,其中被广泛接受的有Mallows模型[23]和Plackett-Luce模型[24].然而,现有工作都限制了用户偏好的类别,主要对Top-k偏好[25]和评价对象子集的排名偏好[26]进行处理,如Plackett-Luce模型处理的偏好类型仅限于Top-k偏好和评价对象子集的排名偏好,这带来更多的认知和沟通需求,同时缺少对更加广泛和现实的成对比较偏好的处理.
上述研究在处理不完整的成对比较形式的序数偏好时存在以下不足:1)由于缺失偏好的影响,直接基于不完整偏好进行评价的结果客观性不足;2)由于通信和查询的复杂性,通过偏好抽取以提高偏好完整性的方法增加了决策成本,同时这种方法往往只适用于选择最优评价对象的场景;3)由于偏好类别的限制,使用排名模型对缺失偏好进行预测的工作不能对使用场景广泛的成对比较偏好进行处理.针对上述问题,本文提出使用Mallows-φ排名模型来对用户缺失的成对比较序数偏好进行预测,进而得出用户的完整偏好.
3 问题定义
为了更好地描述和解决不完整成对比较序数偏好的预测问题,首先对本文相关概念及问题进行定义.
定义1.集合U={u1,u2,…,um]为所有用户的集合,集合S={s1,s2,…,sn}为所有评价对象的集合,其中m为用户的个数,n为所有评价对象的个数.
定义2.si≻sj是关于评价对象si和sj的成对比较偏好,表示评价对象si优于评价对象sj,其中,i,j∈{1,2,…,n},i≠j,si,sj∈S.
定义3.集合vu⊆{(si,sj)|i,j∈{1,2,…,n},i≠j}是用户u(u∈U) 关于S的成对比较偏好的集合.其中,1≤|vu|≤n(n-1)/2,若存在序偶对(si,sj)∈vu则表示表示si≻usj,即用户u认为评价对象si优于评价对象sj.V={vu|u∈U}表示所有用户偏好的集合.
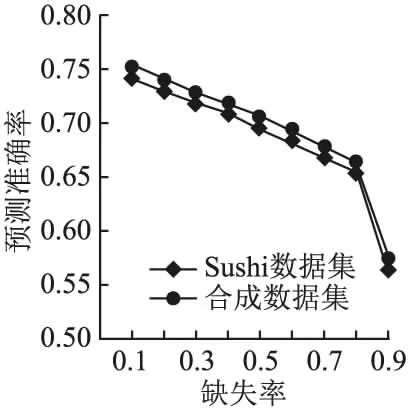
一个完整排名σ0=s1s2…sn表示对集合S中所有评价对象的一个排序.当|vu|=n(n-1)/2时,vu为用户u的完整成对比较偏好,此时vu对应一个完整排名σ0=s1s2…sn,其中,si∈S,i=1,…,n;当1≤|vu| 例如,已知评价对象的集合为S={s1,s2,s3,s4},完整的成对比较集合包含所有评价对象的两两比较.若用户u的不完整偏好集合vu={(s1,s2),(s1,s3),(s1,s4),(s2,s3)},则缺少对s2,s4和s3,s4的成对比较偏好.在已知所有用户的不完整偏好集合V时,本文基于V对每个用户u缺失的成对比较偏好进行预测:首先,使用V来对Mallows-φ模型进行训练;然后,针对单个不完整偏好vu,利用训练得到的模型进行后验采样;最后,基于后验采样的完整排名来对vu缺失的成对比较进行预测,进而得出用户u的完整偏好.若用户的不完整偏好集合vu={(s1,s2),(s1,s3),(s1,s4),(s2,s3)},可根据上述过程预测出该用户缺少的s2,s4和s3,s4成对比较偏好. Mallows-φ模型[27]是基于距离排名评价模型的典型代表,其通过反复进行成对比较来评估评价对象,最终得出排名r的概率分布模型: (1) 该模型通过参考排名σ和分散参数φ∈(0,1]来进行参数化.其中,参数σ表示所有评价对象的一个完整排名,参数φ∈(0,1]表示任意一个完整的序数偏好与σ的分散程度,当φ→0时,所有的偏好相同,当φ=1时,所有的偏好呈现均匀分布.Z=1·(1+φ)·(1+φ+φ2)…(1+…+φn-1),d(r,σ)表示排名r和σ的逆序对个数,即两个排名之间优先关系不同的评价对象的对个数. 任意一个符合Mallows-φ模型分布的完整排名,都是所有评价对象的成对比较结果所对应的一个完整排名,因此,Mallows-φ模型可以很好地对用户的成对比较序数偏好进行建模,进而实现对用户缺失偏好的预测. 在已知所有用户的不完整成对比较偏好时,我们首先使用local Kemenization[28]算法训练出Mallows-φ模型的参考排名.然后在已知参考排名的基础上,使用期望最大化(expectation maximization,EM)算法[29]对Mallows-φ模型的参数进行最大似然学习.以下对Mallows-φ模型训练过程进行详细说明. a)估计模型的参考排名σ Kemeny排名是指与一组排名的逆序对数和最小的一个排名,是Mallows-φ模型的参考排名σ的最大似然估计[30],求Kemeny排名是NP难的[31],而使用local Kemenization算法可以在实践中非常有效地确定一个近似解[28].对于任意一个评价对象的排名σ0=s1s2…sn,σi表示排名σ0的第i个位置的评价对象,local Kemenization算法将σi与σj进行对比,其中i=2,…,n,j=i-1,…,1,且cij表示认为评价对象σi优于σj的偏好vu的个数,若在所有用户的偏好集合V中,cij>cji,则交换σi和σj的位置;若cji>cij,则σi的交换结束,进行σi+1的比较和交换.因此,在已知用户不完整成对比较偏好的情况下,基于算法1估计出模型的参考排名σ. 算法1.local Kemenization算法 输入:所有用户的偏好集合V,任意评价对象的排名σ0=s1s2…sn 输出:模型的参考排名σ 1.FOR(si,sj):si,sj∈Sandi≠jDO 2.cij=|{u∈U:si≻usj}| 3.ENDFOR 4.FORi=2 tonDO 5.FORj=i-1 to 1DO 6.IFcij>cji 7. 交换σi和σj的位置 8.ELSE 9.BREAK 10.ENDIF 11.ENDFOR 12.ENDFOR 13.RETURNσ0 b)估计模型的分散参数φ 我们使用EM算法对分散参数φ进行估计.EM算法是一种流行的最大似然估计方法,适用于概率模型.EM实际上是一种局部搜索算法,它在E和M两个步骤之间交替.E步是计算模型的隐变量的期望值,在使用EM算法对分散参数φ进行估计时,E步则是得出符合用户不完整偏好v约束的一个完整排名:用Ω(v)表示v的补全,即与v一致的完整排名的集合.在已知用户的不完整偏好v的条件下,Mallows-φ后验分布如下: (2) 文献[32]中针对Mallows-φ的后验分布进行采样的算法AMP(Approximate Mallows Posterior),可以对式(2)进行有效采样,进而得到符合用户不完整偏好约束的一个完整排名,即得出EM算法E步中的隐变量的期望值.对于i=1,…,n,AMP算法以概率φi-j/(1+φ+…+φi-1)将σi插入排名r0中的位置j≤i,同时插入位置j要遵循用户偏好v施加的约束,若用户的不完整偏好v中认为σi优于σj,则在AMP基于v采样的排名中,σi放在σj之前,其中,σ=σ1σ2…σn为模型参考排名,σi为评价对象,当i 算法2.AMP算法 输入:用户u的偏好v,Mallows-φ模型的参考排名σ=σ1σ2…σn,Mallows-φ模型的分散参数φ,一个空的排名r0 输出:采样的排名r0 1.r1=σ1 2.FORi=2 tonDO 3.Li={i′ 4.Hi={i′ 6.ENDFOR 7.RETURNr0 EM算法的M步是对模型的未知参数进行最大似然估计.因此,从每个用户的不完整偏好v的后验分布采样一个完整排名,然后利用所有采样的完整排名集合R计算分散参数的最大似然估计,可得: (3) 算法3.不完整排名下分散参数的估计算法 输入:模型参考排名σ,模型分散参数的初始猜测值φ0,所有用户不完整偏好vu的集合V,收敛阈值θ为0.000001,EM迭代次数maxRounds设置为100. 1.FORi=1 to 100DO 2.R=∅ 3.FORv∈VDO 4.R←AMP(σ,φi-1,v) 5.ENDFOR 6.φi=value(R,σ) 8.IFφi-φi-1≤θ 9.BREAK 10.ENDIF 11.ENDFOR 算法1的local Kemenization算法用来估计模型的参考排名,时间复杂度为mn2.在算法2中,利用AMP算法为每个用户采样完整排名的时间复杂度为O(mn).算法3为了对模型的分散参数进行估计,首先运行m次AMP采样算法,其时间复杂度为O(m2n),然后利用采样的完整排名估计分散参数的时间复杂度为O(mn2),则算法3的时间复杂度为O(mn2+m2n).对Mallows-φ模型的训练就是估计模型的参考排名和分散参数,因此训练Mallows-φ模型的时间复杂度为O(mn2+m2n),其中,m是用户的个数,n是评价对象的个数. 在已知所有用户的不完整偏好集合时,首先基于V对Mallows-φ模型进行训练,然后才能利用训练出的模型对用户的缺失偏好进行预测.因此,在基于用户的不完整偏好对Mallows-φ模型进行训练之后,预测用户缺失偏好的过程如下: 1)在基于不完整成对比较偏好对Mallows-φ进行训练后,可以得出模型的参考排名σ和分散参数φ,进而得出所有用户偏好所符合的Mallows-φ分布: 2)将训练出的模型依次以用户u的不完整偏好vu为条件,以获得vu所有可能的完整偏好的后验分布,即符合vu约束的排名的概率分布: 3)使用AMP后验采样算法对基于vu的后验分布进行采样,得到符合vu约束的完整排名集合Vu. 4)最后,根据采样的排名集合Vu对vu中缺失的成对比较进行预测:在采样的排名集合中,若有超过一半数目的排名认为缺失的si和sj的成对比较结果为si优于sj,则预测结果为si≻sj. 5)对每个用户的不完整偏好执行上述预测过程,得出对所有用户的完整成对比较偏好的预测. 为了验证在成对比较形式的用户偏好下预测缺失偏好的有效性,进行了偏好预测的有效性分析估、模型训练的准确性评估和性能分析3个实验,实验环境为:Inter Core I7 CPU,64位Win10操作系统,开发环境为PyCharm 2019.3,开发语言为Python 3.5.实验采用Mallows人工合成数据集和Sushi真实数据集,通过评估在人工合成数据集和真实数据集上的实验结果来验证偏好预测的有效性和准确性.其中,Sushi数据集由5000条关于10种寿司的完整序数偏好组成.Mallows-φ模型是通过参考排名σ和分散参数φ来进行参数化,可以通过设置不同的参数σ和φ,随机生成不同分布下的序数偏好数据集:参数σ是由n个评价对象构成的完整序数偏好,参数φ∈(0,1]控制随机生成的序数偏好与σ的分散程度,当φ→0时,生成的所有偏好相同,当φ=1时,生成的偏好均匀分布.因此,通过设置不同的σ、φ、用户数目m和评价对象数目n,进而得到Mallows人工合成数据集,其中,设置评价对象数目n为10、20、30,用户数目m为300、500、700、1000,分散参数φ为0.3、0.5、0.7,参考排名设置为相应的评价对象的随机排名. 本节首先在Sushi数据集和合成数据集上进行实验,以分析偏好预测的准确率.此外,协同过滤方法通过分析指定用户的偏好,在所有用户中找到该用户的相似用户,然后通过这些相似用户的偏好对该用户缺失的偏好进行预测,因此协同过滤方法能够有效利用其他相似用户的偏好,进而对指定用户缺失的偏好进行预测,并且协同过滤方法在推荐系统等领域得到了广泛应用.文献[33]的协同过滤方法对用户的不完整序数偏好进行预测,因此,将本文方法与该协同过滤方法进行对比,以验证本文方法的有效性. 5.1.1 偏好预测的准确性分析 在预测实验中,评估学习到的模型在预测缺失的成对比较时的性能.在生成合成数据集时,评价对象数目为10,偏好个数为5000,参考排名随机生成,分散参数的值为1,使得生成的偏好呈现均匀分布.在Sushi数据集和合成数据集上,对每个完整序数偏好进行成对比较的随机缺失,即把完整序数偏好转换为任意两个评价对象的成对比较集合,然后对成对比较集合中的元素进行随机缺失.在对偏好进行随机缺失之后,利用得到的不完整偏好对模型进行训练,然后基于训练后的模型对用户缺失的偏好进行预测. 预测完成后,对预测的准确率进行度量.对于任意缺失的成对比较,若预测结果与相应的完整数据中的结果一致,则对这个缺失的成对比较预测准确.因此,通过统计所有缺失的成对比较的预测结果来度量预测的准确率.首先计算出预测的偏好与相应的合成数据中的完整排名的逆序数目,然后求得该逆序个数占缺失的成对比较个数的百分比,作为预测误差的度量,同时预测准确率为1-α.结果如图1所示. 图1 偏好预测的准确性评估 由图1可见,随着偏好缺失率的增加,预测准确率逐渐降低.对于Sushi数据集,当缺失率为0.1时,预测准确率为0.740933,随着缺失率的增加,预测准确率逐渐降低,当缺失率为0.8时,预测准确率为0.654067.当缺失率为0.9时,预测准确率为0.563061.此外,对于合成数据集,预测准确率也是随着缺失率的增加而降低,缺失率相同时,合成数据集下的预测准确率接近且略高于Sushi数据集下的预测准确率. 5.1.2 对比实验 文献[33]的协同过滤方法可以对序数偏好进行预测:首先在所有用户中找到该用户的相似用户,然后通过这些相似用户的偏好对该用户缺失的序数偏好进行预测,该协同过滤方法有效利用了相似用户的偏好,从而可以用户的缺失偏好进行较准确的预测.因此将本文方法与该协同过滤方法进行对比,通过比较两种方法对用户缺失偏好的预测准确率,来验证本文方法的有效性. 在Sushi数据集和Mallows合成数据集上进行对比实验,其中,合成数据集是通过设置随机参考排名σ,分散参数φ=0.5,用户数目m=1000和评价对象数目n=1得到的Mallows人工合成数据集.首先,在预设的缺失率下,对每个用户的序数偏好进行随机缺失,得到不完整偏好;然后,在不完整偏好的基础上,分别使用本文方法和协同过滤方法对用户完整偏好进行预测;最后,比较两种方法对用户缺失偏好的预测准确率.在Mallows合成数据集和Sushi数据集上的结果分别如图2所示. 图2 两种方法的偏好预测结果对比 由图2可知,随着用户偏好缺失率的增大,本文方法和协同过滤方法预测准确率都在下降,同时,由于合成数据集的偏好数目小于Sushi数据集,两种方法在合成数据集上的预测准确率都小于在Sushi数据集山的预测准确率.然而,在任意缺失率下,本文方法的预测准确率都比协同过滤方法的预测准确率高. 基于所有用户不完整偏好对Mallows-φ模型进行训练,然后利用训练出的模型对缺失偏好进行预测,因此EM算法训练出的模型的准确性决定了预测结果的准确程度.以下实验分别在合成、Sushi数据集上通过对数似然比检验方法来验证训练出的模型的准确性. 对数似然比检验是一种检验参数能否反映真实约束的方法,通过对数似然比检验可以评估训练出的模型的准确性.因此,分别计算测试数据在完整偏好的真实分布上的对数似然函数值L1、在基于不完整偏好训练出的模型上的对数似然函数值L2,然后L2/L1的值越小,则说明训练出的模型越接近数据真实分布. 在合成数据上进行了3个实验,其中,每个实验只对数据集的单个变量进行改变:(a)改变成对比较偏好的缺失率α;(b)改变评价对象的数量n;(c)改变提供偏好的用户的数量m.在每个实验对单个变量进行改变时,用α=0.6,n=20,m=100来固定另外两个参数.此外,在每个实验中,Mallows-φ模型的参数设置如下:参考排名σ均匀随机产生;φ值从[0.2,0.8]中均匀随机产生,且合成数据是使用具有这些参数的Mallows-φ生成的,每个参数设置取30次运行结果的平均值,然后通过对数似然比来分析模型训练的准确性,结果如图3所示. 由图3可见,用户偏好的缺失率越小,模型的训练结果越准确.缺失率为0.1时,对数似然比为1.000602,随着缺失率增加,对数似然比逐渐增加,缺失率为0.7时,对数似然比增加到1.071519,而当缺失率达到0.8时,对数似然比显著增加,值为1.325852,由此可知,当用户偏好的缺失率不大于70%的时候,一直能得到较好的模型训练效果.当固定偏好缺失率和评价对象个数时,随着用户偏好数量的增加,即用于训练的偏好数据增多,对数似然比逐渐减小,说明模型训练结果更加准确.当固定缺失率和用户偏好的数量时,随着评价对象数目的增加,对数似然比也逐渐减小,说明模型的训练效果更加准确. 图3 模型训练的准确性评估(合成数据) 寿司数据集包含10种寿司的5000个完整排名,表明对寿司的偏好.在Sushi数据下进行模型训练的准确性评估时,使用3500个偏好进行训练,使用1500个偏好进行验证.首先,基于3500个偏好,通过设置不同的缺失率α对完整偏好的成对比较进行随机缺失,获得不完整偏好,然后使用不完整偏好运行EM算法对模型进行训练,得出模型的参数,最后评估每个缺失率下学习出的模型与完整排名下的模型在验证数据上的对数似然比,每个缺失率下运行了30次EM并对其结果求平均值.结果如图4所示. 由图4可见,在Sushi数据下,缺失率为0.1时,对数似然比为0.000058,随着缺失率的增加,对数似然比缓慢增大,缺失率为0.8时,对数似然比为1.003275,而缺失率为0.9时,对数似然比为1.015964,发生显著变化,因此,在真实数据下,缺失率不大于80%时,利用不完整偏好运行EM算法,训练出的模型都非常接近完整排名下的真实模型.由合成数据上对EM算法的评估可知,偏好数量越多,模型的训练效果越好,因此,使用3500个偏好能得到很好的训练效果. 为验证方法的运行效率,通过改变用户偏好个数、评价对象个数和缺失率进而得到不同的合成数据集并进行实验,每个实验中,用缺失率α=0.6,评价对象个数n=10,用户偏好个数m=100来固定另外两个参数,并且记录了每次实验的运行时间,如图5所示. 由图5可见,缺失率、偏好个数、评价对象个数中的任意两个参数固定不变时,随着另一个参数的增加,算法运行时间增大,而且,缺失率和偏好个数的改变对运行时间的影响缓慢,当评价对象的个数增加时,算法运行时间显著增大. 为了解决序数偏好不完整的问题,本文基于概率排名模型,对用户不完整的成对比较形式的偏好进行预测,进而得出用户的完整偏好.成对比较形式的序数偏好更加广泛和现实,而且考虑了用户对不同评价对象之间的偏好关系,解决了不同用户的评价准则不一致的问题. 由于不同用户可能存在不同的偏好类型,因此下一步的研究工作将聚焦于如何对用户进行分割或聚类,在不同的用户类型下对不完整偏好进行预测.4 基于Mallows-φ模型的不完整偏好预测
4.1 基于不完整成对比较偏好的Mallows-φ模型训练
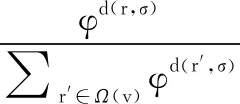


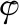
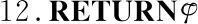
4.2 预测不完整成对比较偏好

5 实验结果与分析
5.1 有效性实验

5.2 模型训练的准确性评估


5.3 性能分析
6 结 论
