面向受损网络嵌入的深度降噪自编码器模型

李智杰，王启辉，李昌华，张 颉

(西安建筑科技大学 信息与控制工程学院，西安 710055)

1 引 言

现今，网络无处不在，抖音、今日头条、微信等社交平台，用户与用户之间形成了社交网络，不同地域不同语言形成了语言网络，公司内部员工之间邮件往来形成了邮件网络[1].通过对这些网络的学习以及挖掘网络中的信息，对分析网络的性质和结构具有积极的作用，如对抖音的推广应用方面为用户推荐好友或感兴趣的内容等[2].

如何分析和学习网络中的信息，其中一个基本且核心的关键问题是如何对网络进行有效快速的学习[3].一是图核算法，使用核函数来测量网络之间的半正定网络相似度[4].二是将网络降维到低维空间(网络嵌入)，通过顶点的向量表示，精确地捕获节点之间的结构关系[5]，目的是在学习的嵌入空间中重建网络.因此，可以直接在低维空间中挖掘网络中的信息，例如信息检索[6]、分类[7]和聚类[8].学习网络特征主要面临以下问题：如何捕获高度非线性[9]的网络结构[10]，如何保持局部和全局结构，以及由于网络稀疏性[11]导致的链路预测性能的不足.

目前图领域已经存在很多网络表示方法：基于因子分解的Laplace eigenmaps[12]和Graph Factorization；针对浅层网络的Line[13]和Node2vec；以及近年提出的结构深度网络嵌入模型(Structural Deep Network Embedding，SDNE).结构深度网络嵌入模型是一种基于深度学习[14]的网络嵌入模型，通过一个半监督深度自编码器模型来捕获高度非线性网络结构，利用一阶和二阶相似度来表征局部和全局网络结构，旨在解决结构保持和网络稀疏性问题，在网络重构和链路预测方面表现出比传统方法更好的效果[15].

结构深度网络嵌入模型能很好的保留网络的局部和全局结构信息，但对于受损网络，该模型所使用的自编码器在学习过程中对受损网络进行编码解码时，面对缺失或遭到污染的数据，在低维空间中学习得到的嵌入向量不能很好地重构原有的网络结构，存在一定缺陷.基于此，本文通过加入降噪自编码器(Denoising auto-encoder，DAE)[16]来对现有的SDNE模型进行改进，主要用来提升模型对受损网络的网络重构和链路预测能力，同时提升模型的泛化能力和抵抗噪声能力.

2 结构深度网络嵌入模型与降噪自编码器

在本节中，首先定义网络表示，然后对结构深度网络嵌入模型的基本结构进行介绍，最后对现有的降噪自编码器模型进行简要介绍.

2.1 网络表示定义

网络嵌入的目的是将网络中的节点映射到一个低维潜在空间，得到的低维节点向量能保留局部和全局结构特征，可以直接实现网络计算，并能运用到网络重构、节点分类和链路预测等多种网络应用领域，如图1所示.

图1 网络表示概念图

2.2 结构深度网络嵌入模型

结构深度网络嵌入模型是一个半监督深度神经网络模型，整个模型可以分为两个部分：一个是监督的拉普拉斯特征映射对一阶相似度进行建模的模块；另一个是无监督的深度自编码器对二阶相似度进行建模的模块.通过半监督深度神经网络进行联合优化，使模型在保留全局网络结构的同时保留局部的结构特征，增强算法在稀疏网络中的鲁棒性.

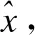
图2 SDNE模型

2.3 降噪自编码器

自编码器(Auto-encoder，AE)是经典的深度学习模型之一，是目前应用较为广泛的降维方法，通过对多层神经网络训练，将高维数据转换为低维数据.自编码器是典型的3层神经网络由输入层、隐藏层和输出层构成，编码过程在输入层和隐藏层之间完成，解码过程在隐藏层和输出层之间完成.DAE是AE的一种变形，该模型不仅可以去噪，还可以学习到一个更好的网络表示.通过DAE学习到的表示可以被用来预训练更深的无监督网络或者有监督网络.与稀疏自编码器、稀疏编码、收缩自编码器等正则化的自编码器类似，DAE的优势是避免了编码器和解码器学习的结果是无效的恒等函数，同时编码器允许学习的容量很高.

2.4 拉普拉斯特征映射

拉普拉斯特征映射(Laplacian Eigenmaps，LE)利用节点对的相似度来保持网络的性质，具有相似度的节点在网络嵌入过程，被映射到向量空间中的距离很近，就可以在降维后保持原有的网络结构，如果相似的节点对被映射到向量空间中的距离很远，就给予这对节点更大的罚值.拉普拉斯特征映射可以通过捕获网络的一阶相似度来保留网络的局部结构.基于这一思想，该方法使用如下目标函数来实现节点对的低维映射：

y=∑i≠j(yi-yj)2Sij=2yTLy

(1)

(2)

3 结构深度降噪网络嵌入模型

传统的自编码器在面对受损网络和稀疏网络时所使用的重建标准不能保证提取有用的特征，会导致得到的输出结果是简单的复制输入，为此本文通过对降噪自编码和结构深度网络嵌入模型的学习了解，提出了半监督的结构深度降噪网络嵌入模型(Structural Deep Denoising Network Embedding，SDDNE).该模型通过对DAE的堆叠来捕获二阶相似度(保留网络的全局结构)，由拉普拉斯特征映射捕获一阶相似度(保留网络局部结构).

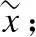
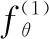
图3 结构深度降噪网络嵌入模型

(3)

gθ′(y)=s(W′y+b′)

(4)

参数集为θ′={W′，b′}.堆叠降噪自编码器的目标是最小化输入和输出的误差，损失函数如下：

(5)

利用重构准则可以平滑的捕获数据流形的优势，避免了最小重构误差在阐述样本相似度上的局限，在一定程度上保持了样本之间的相似度.如果使用邻接矩阵S作为堆叠降噪自编码器的输入，重建过程将使具有相似邻域结构的顶点具有相似的表示.由于网络的特定特性，这种重建过程不能用于本文要解决的问题.在网络中，可以观察到一些链接，但同时许多合法链接没有被观察到，这意味着顶点之间的链接确实指示它们的相似度，但没有链接不一定表明它们不具备相似度.通过对非零元素的重构误差施加更多的惩罚来进一步解决网络稀疏性的问题.修改后的目标函数如下所示：

(6)

对于高度非线性网络结构，不仅需要保留全局网络结构，还需要保留局部网络结构.本文使用一阶相似度来表示局部网络结构，借用拉普拉斯特征映射的思想.当相似顶点被映射到嵌入空间的距离较远时，就会产生惩罚，从而使得由一条边连接的顶点在嵌入空间中距离相近，从而保证了一阶的相似度.一阶相似度损失函数如下：

(7)

为了同时保持一阶和二阶相似度，将损失函数联合起来，加上正则项后得到了模型的整体目标函数：

Lmix=αL2nd+βL1st+νLreg

(8)

其中，Lreg为防止过拟合的L2范数正则项：

(9)

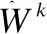
(10)

SDNE采用sigmoid作为激活函数，但通过该激活函数方向传播时，容易在两端产生饱和神经元，导致权值无法更新，引起梯度消失现象，使深度学习训练时出现节点间区分度较低的问题.为了避免上述问题，SDDNE采用线性整流函数(Rectified Linear Unit，ReLU)作为激活函数代替sigmoid.相较于sigmoid激活函数，ReLU具有计算速度快的优势，并且由于ReLU是分段线性函数，梯度下降和反向传播效率更高，避免了梯度爆炸和梯度消失问题.SDNE采用了SGD优化神经网络，虽然SGD训练速度快，但是本身的收敛速度较慢，准确度下降较快，容易陷入鞍点，得不到全局最优结果.SDDNE采用自适应矩估计(Adaptive Moment Estimation，Adam)优化器，Adam优化器善于处理稀疏梯度和非平稳目标，并且在大数据集和高维数据空间可以更好的加速神经网络收敛.SDDNE模型的训练复杂度为O(ncld)，n为顶点数，d是隐藏层最大维数，c是网络平均度，l是迭代次数.具体算法如下：

算法.SDDNE半监督深度模型训练算法

输入：G=(V，E)的邻接矩阵S，权重值W，偏重值b，超参数α和υ；

输出：网络表示Y，更新后的参数θ和重构误差LH；

Step 1.初始化参数θ；

Step 2.X=S；

Step 3.重复上述操作；

Step 10.重复过程Step 4-Step 9；

Step 11.直到迭代结束；

4 实验结果及分析

为验证模型在不同比例噪声污染下网络重构和链路预测的实际效果，对数据集进行了训练和测试，针对SDNE、LINE、DeepWalk等不同模型分别做了对比实验.

4.1 数据集

本文选用BLOGCATALOG社交网络数据集和ARXIV GR-QC语言网络数据集，社交网络数据集是在线用户的社交网络，每个用户至少有一个类别，这些类别可以作为每个顶点的基本属性，ARXIV GR-QC涵盖来自ARXIV的广义相对论和量子宇宙学领域的论文.在这个网络中，顶点代表作者，边表示作者在arXiv中共同撰写了一篇科学论文.

表1 数据集信息

4.2 实验设置

为了验证本文提出SDDEN模型的先进性，选择保持一阶、二阶相似度的SDNE，LINE网络嵌入模型以及保持二阶相似度的DeepWalk网络嵌入模型在不同数据集中分别进行对比实验.

SDNE：利用拉普拉斯特征映射与自编码器联合优化，同时保持网络一阶、二阶相似度并以此来学习网络的局部和全局特征.

LINE：通过定义损失函数，分别保持网络的一阶、二阶相似度，通过KL散度，最小化邻接矩阵生成的节点对概率分布和由嵌入内积产生的概率分布之间的距离，最终实现嵌入最优化.

膜蒸馏(Membrane Distillation，MD)是一种热驱动的水处理方法，其中较热的进料流在疏水的微孔膜的一侧流动，而较冷的馏出物流在另一侧流动。膜两端的温差产生蒸汽压差，使得液态水从进料流中蒸发，通过膜孔，并冷凝成馏出物流。其广泛应用在海水淡化、超纯溶液浓缩与提纯等方面 [1-3]。

DeepWalk：基于Word2vec的网络嵌入算法，利用Skip-Gram模型将节点映射为低维嵌入向量，可以保持网络的二阶相似度.

本文采用了多层堆叠降噪自编码器结构，BLOGCATALOG和ARXIV GR-QC数据集使用3层编码器，隐藏层的节点数为100，1000和10000.SDDNE激活函数为ReLu，优化器采用Adam，通过网格搜索来进行调整，学习速率为0.01，SDDNE模型损失函数由前期的一阶相似度损失和后期的二阶相似度损失联合组成，通过对模型的训练，发现当迭代次数超多60次时，两次迭代之间权值误差变化极小，达到了模型训练结束所设定阈值，模型收敛，为此实验中模型迭代次数为60.SDNE激活函数为sigmoid，优化器采用SGD.LINE随机梯度下降的批量大小设置为1，初始学习速率为0.25，DeepWalk窗口大小为15，步长为60，每个顶点游走距离为60.

4.3 评估指标

在网络重构和链路预测实验中，采取precision@k和平均精度两种评估指标来评估模型性能.precision@k通过给返回的实例提供相同的权重来进行度量，定义如式(11)所示：

(11)

式(11)中：V是顶点集，index(j)表示第j个顶点a的排序索引，Δi(j)=1表示顶点vi和vj之间有链接.

平均精度(Mean Average Precision，MAP)中Average Precision是对单个查询的精度求取其均值，加入Mean则是对所有查询的平均精度进行取均值计算，所以MAP具有良好的区分性和稳定性，并且对返回项中排名靠前的尤为关注.

(12)

(13)

式(13)中Q为查询集.

4.4 实验结果分析

4.4.1 网络重构

一个好的网络嵌入模型应该保证学习到的嵌入向量能够保持原有的网络结构.通过对本文所提出SDDNE与不同的网络嵌入模型在网络重构能力方面进行对比实验，从而验证SDDNE在实际应用中的通用性.使用语言网络ARXIV GR-QC和社交网络BLOGCATALOG作为代表.给定一个网络，在不同的噪声污染比例下使用不同的网络嵌入模型来学习网络表示.由于原始网络中的现有链路是已知的，用来作为基础样本与重构后的网络表示进行对比，可以评估不同方法的重构性能.用k-precisiion和MAP作评估指标，衡量前k条边被准确重构的比例.实验结果如图4所示.

由图4整理得到在不同噪声污染条件下，不同模型在网络重构测试中对网络边准确重构的Average precision如表2所示.

图4 网络重构准确率

以下为评估指标MAP在数据集BLOGCATALOG和ARXIV GR-QC中面对不同比例噪声干扰的网络重构任务的实验结果.

结合表2可以得到在ARXIV GR-QC数据集上随着噪声污染的增加，SDDNE网络重构任务的k-precisiion均值分别为98.07%，84.89%，77.83%，BLOGCATALOG数据集上，SDDNE在5%，10%，20%噪声污染下进行网络重构的k-precisiion均值分别为68.32%，65.79%，64.42%，与SDNE，LINE，DeepWalk等方法相比，在受损网络的重构上具有非常明显的优势.图5实验结果表明，在ARXIV GR-QC和BLOGCATALOG数据集中各模型进行网络重构任务时随着噪声添加比例的增加MAP均有所下降，但SDDNE能够一直保持较高的重构平均准确率.

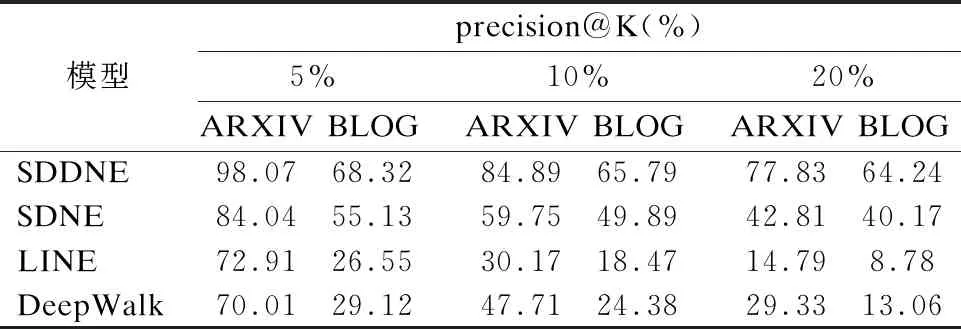
表2 网络重构准确率

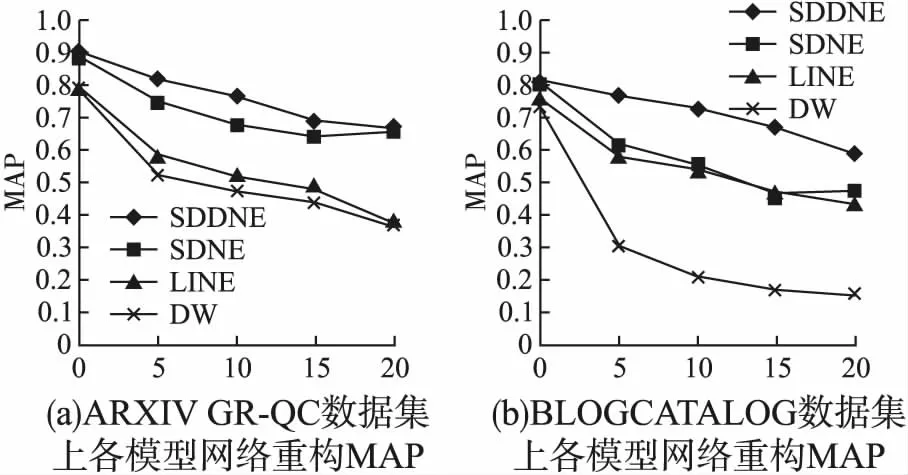
图5 不同噪声污染下网络重构MAP

综上所述，SDDNE在受损的社交网络和语言网络中进行网络重构任务具有很好的准确率和稳定性.虽然SDDNE，SDNE，LINE都是利用一阶和二阶相似度来保持网络结构，但是SDDNE具有更好的重构性能.主要原因是，LINE模型采用浅层结构，无法捕获网络中的高度非线性结构，SDNE模型也是深度模型，但是对于受损网络中被污染的结构难以很好的进行网络重构，鲁棒性不够好.综上所述，无论是在准确率还是稳定性上SDDNE比其他网络嵌入模型具有更好的优势.

4.4.2 链路预测

为了评估SDDNE在链路预测任务中的整体性能，在本节中使用数据集BLOGCATALOG进行训练，与SDNE、LINE、DeepWalk进行对比.在本部分实验中，随机隐藏所选取链接数的20%，通过模型训练得到每个顶点的表示，使用获得的表示来预测未被观察到的联系，与网络重构不同的是，链路预测实验是为了预测未知或可能存在的链接，而不是重建现有链接，因此可以得到不同模型的链路预测能力.precision@k作为评估指标，链接数从10逐渐增加到10000.实验结果如表3所示.

表3 链路预测准确率

分析表3可知，当链接数k小于100时，所有的网络嵌入模型都有很好的链路预测能力，但当k的值逐渐增大到1000时，除了SDDNE可以保持90%以上的预测能力，其他模型都不能得到很好的学习表征.随着k的增加，SDDNE的性能始终优于其他网络嵌入方法，表明该方法学习的表征对新的链路具有更好的预测能力.

5 结 语

本文针对现有结构深度网络嵌入模型在处理受损网络时，在低维空间中学习得到的嵌入向量无法很好的重构原有网络结构的缺陷，从降噪的角度入手，通过引入降噪自编码器并且进行堆叠，得到了改进的SDDNE模型.SDDNE模型通过堆叠降噪自编码器来捕获二阶相似度以此保留网络的全局结构，通过拉普拉斯特征映射捕获一阶相似度来保留网络局部结构.SDDNE解决了SDNE使用SGD优化模型而产生的误差变小和训练无效的问题，同时对受损网络进行网络重构和链路预测任务时均取得了更好的重构准确率和链路预测准确率.并且SDDNE模型很好的避免了传统降噪自编码器单层的模型结构在处理高度非线性复杂网络结构时无法很好的保持网络结构特征的问题，模型具有更好的鲁棒性.但在针对不同网络结构，如何得到最优的降噪自编码器噪声添加比例，尚需进行研究.