缩放残差前置GRU模型

吴晓丹，石 争，郑玉蒙，武优西，商博雅

1(河北工业大学 智慧医疗实验室，天津 300401)

2(河北工业大学 人工智能与数据科学学院，天津 300401)

1 引 言

目前，循环神经网络(Recurrent Neural Networks，RNN)广泛应用于语音识别、语言模型、机器翻译等领域，可通过记忆模块有效建模序列信息，其具体表现为长短期记忆网络(Long-Short Term Memory，LSTM)与门控循环单元网络(Gated Recurrent Unit，GRU)[1].虽然上述二者均通过引入门控机制控制序列信息的流失与积累，缓解了简单RNN中普遍存在的长期依赖问题[2]，但相较LSTM，GRU因使用更新门控制当前状态的保留与更新，具有参数量与计算量小、运行速度快等优势[3，4].

然而，由于GRU使用sigmoid或tanh等饱和激活函数，模型深度增加易引发梯度消失与退化问题，进而严重降低模型训练速度及性能[5].针对梯度消失问题，已有GRU研究提出采用层标准化方法(Layer Normalization，LN)缓解并取得了可观结果，但模型退化问题仍未得到有效解决[6].

此外，退化问题同样存在于卷积神经网络(Convolutional Neural Network，CNN)等前馈神经网络(Feedforward Neural Networks，FNN)模型，其相关研究采用高速公路连接(Highway Networks，HW)和恒等残差连接(Identify Residual Network)等直连结构(Shortcut Structure)缓解因模型深度增加而带来的退化问题[7,8].然而，本文深入分析应用饱和激活函数的GRU发现，恒等残差直连结构不仅易遮盖有效信息，同时大幅提高梯度消失可能性.即使现有相关研究应用高速公路网络筛选信息缓解上述遮盖问题，但门控机制因引入额外的非线性计算严重阻碍梯度反向传播.

受此启发，本研究提出缩放残差前置(Scale Residual before LN)GRU模型，使用缩放残差连接(Scale Residual Network)替代恒等残差连接以防止信息遮掩，并新增线性信息筛选模块替代高速公路连接中的非线性门控机制，最大限度保留有效信息并缓解退化现象[9-11]；同时，设计直连结构前置于层标准化形成直连前置结构(Shortcut before LN)，防止直连结构中引入额外的非线性计算以便于不同层间的梯度传播，最终有效改善模型退化问题并进一步防止梯度消失现象发生.

2 相关技术

2.1 门控循环单元网络

rt=σ(Wr[xt，ht-1]+br)

(1)

zt=σ(Wz[xt，ht-1]+bz)

(2)

(3)

(4)

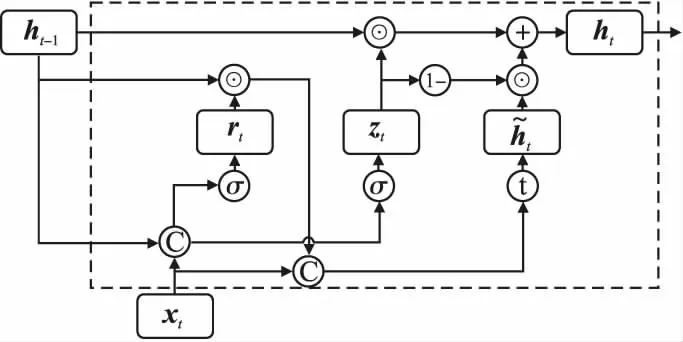
图1 GRU循环单元结构

2.2 层标准化

模型深度增加导致梯度爆炸、梯度消失现象发生，隐藏层输入的数据分布出现较大波动，进而导致模型训练困难[12].层标准化方法可以将深度学习模型中隐藏层输入的数据分布控制在确定范围，消除内部协方差变化，有效缓解梯度爆炸和梯度消失现象，降低模型训练难度.该方法不依赖于批次大小和输入序列长度，因此，将其应用于输入序列长度不确定的RNN等结构时可取得良好效果，计算过程如式(5)～式(7)所示：

(5)

(6)

(7)

2.3 高速公路连接

T=σ(Wx+b)

(8)

C=1-T

(9)

H(x)=T⊙F(x)+C⊙x=F(x)+C⊙(x-F(x))

(10)

其中，门控T使用σ作为激活函数，W和b为门控机制的权重和偏置向量，C与T互补，H(x)是高速公路连接的最终输出.

2.4 恒等残差结构

恒等残差结构是另一种用于解决退化现象的直连结构，与高速公路连接相比，该结构不需引入额外的参数和门控单元，而是以恒等残差连接替代门控连接，通过去除直连结构中的非线性计算，使其保持模型复杂度的同时实现梯度的有效传递，引入的额外计算量为o(dmodel)[13，14].

假设神经网络输入为x，输入与输出的映射关系为F(x)，最优映射关系为H(x).未引入残差模块时，用F(x)拟合H(x)；引入残差模块后，残差神经网络将网络结构拆分为残差映射F(x)与恒等映射x两个分支.基于所搭建的恒等映射，F(x)拟合对象变为H(x)-x，此时梯度通过残差连接围绕1浮动，缓解梯度消失和退化问题，计算过程如式(11)～式(12)所示：

RES=x

(11)

output=F(x)+RES

(12)

其中，x为当前隐藏层的输入，RES表示恒等残差映射，output表示最终输出.恒等映射RES通过实现上下层间梯度和信息的线性传递，进而缓解深层模型的退化问题，使得模型优化速度更快、表现更好.

3 基于GRU的缩放残差直连前置模型

3.1 模型设计

由于GRU使用sigmoid和tanh等饱和激活函数，因此在模型深度增加时依然会出现梯度消失和退化现象.为此，本文提出缩放残差前置GRU模型，计算过程如图2所示.该模型架构的改进主要包含两点：1)针对传统直连结构中恒等残差连接对GRU的信息遮掩效果以及高速公路连接引入额外参数和非线性计算阻碍梯度传播的缺陷，本文提出缩放残差连接(Scale Residual Network)，通过线性信息筛选模块替代非线性门控机制，不需要引入非线性计算即可实现对信息的筛选，以防止有效信息被覆盖；2)分析直连结构和层标准化相对位置不同对梯度的影响，提出直连前置结构以防止在直连结构中引入非线性计算，使得梯度以线性形式在不同层间流通.

图2 缩放残差前置GRU模型

(13)

(14)

rt=σ(Wirxt+Whrht-1+br)

(15)

zt=σ(Wizxt+Whzht-1+bz)

(16)

(17)

(18)

(19)

其中Sl为缩放模块Scale，为可学习参数，在每个时间步共享参数，形状与单个时间步的输入保持一致，通过按位相乘⊙不需引进非线性计算即可实现上下层之间梯度的有效传递，引入的额外计算量和参数量为o(dmodel).下文将针对缩放残差连接实现信息筛选和直连前置结构对梯度传播的影响进行进一步阐述.

3.2 缩放残差连接

尽管已有研究将恒等残差连接应用于LSTM，但是未充分考虑激活函数对恒等残差连接的影响.该节将针对前向传播过程中不同直连结构对信息前向传播的影响进行分析，以证明缩放残差连接对信息筛选的有效性，将直连结构应用于GRU时，其计算流程图如图3所示，其中Shortcut表示直连结构，将于后文分别描述其具体形式.

图3 添加直连结构的GRU模型

当应用恒等残差连接时，不需要引入额外的参数，计算量为o(dmodel)，计算过程如式(20)所示：

(20)

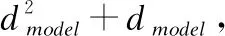
(21)

C=1-T

(22)

(23)

尽管高速公路连接在恒等残差连接的基础上对残差分支的信息进行了筛选，但是存在复杂度高参数量大的问题，为此本文提出一种缩放残差连接通过线性信息筛选模块Sl替代非线性门控机制，引入参数量为引入的参数量为dmodel，计算量为o(dmodel)，复杂度远低于高速公路连接，计算过程如式(24)所示：

(24)

后文将针对不同直连结构对信息的筛选功能进行阐述.

恒等残差连接常应用于使用非饱和函数Relu作为激活函数的CNN中，RES和F(x)的取值范围差异较小.当恒等残差连接应用于使用饱和激活函数的GRU时，对于第l层，计算过程如式(25)～式(30)所示：

(25)

rt=σ(Wirxt+Whrht-1+br)

(26)

zt=σ(Wizxt+Whzht-1+bz)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

rt=σ(Wirxt+Whrht-1+br)

(35)

zt=σ(Wizxt+Whzht-1+bz)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

数据量较大时，训练模型可通过学习Si值，在不引入非线性门控单元前提下，缩放残差连接可以实现有效信息的筛选并保证其良好流通.

3.3 直连结构与层标准化相对位置分析

以恒等残差连接为代表的直连结构与层标准化方法可从不同角度降低模型训练难度.当二者同时应用于GRU模型时，其相对位置会直接影响模型性能.依据直连结构和层标准化相对位置不同，模型分为直连前置结构(Shortcut before LN)和直连后置结构(Shortcut after LN)，具体如图4所示.该节将针对在反向梯度传播过程中不同连接方式对梯度的影响进行分析，进而验证直连前置结构的有效性.

图4 直连前置结构和直连后置结构

对于层标准化对梯度传播的影响，设xl共包含d个元素，E(xl)为xl的均值，S(xl)为xl标准差，二者均为实数.取yl=xl-E(xl)，使用矩阵表示yl如式(43)所示：

(43)

其中E为单位矩阵，I表示元素全部为1的长度为d的行向量，yl关于xl偏导的Jacobian矩阵如式(44)所示：

(44)

(45)

(46)

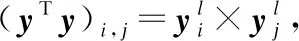
(47)

LN(xl)关于xl偏导如式(48)所示：

(48)

直连前置结构中直连结构位于层标准化前方，如图4(a)所示，l层的输出xl直接产生两分支，一支作为直连结构的输入，另一支被层标准化处理后作为GRU的输入.两个分支输出之和将作为该l层的最终输出，计算过程如式(49)～式(51)所示：

SHl+1=shortcut(xl)

(49)

outputGRU=GRU(LN(xl))

(50)

outputll+1=SHl+1+outputGRU

(51)

假设最终损失函数为Loss，则l层的输出xl关于Loss的偏导计算过程如式(52)所示：

(52)

直连后置结构中直连结构位于层标准化后方，如图4(b)所示.首先，层标准化处理l层的输入xl，接着分为两支路径，一支作为直连结构的输入，另一支作为GRU的输入.上述两支输出之和即为该层的最终输出，计算过程如式(53)～式(56)所示：

(53)

(54)

(55)

outputl+1=SHl+1+outputGRU

(56)

假设最终损失函数为Loss，则l层的输出xl关于Loss的偏导计算过程如式(57)所示：

(57)

综上所述，当直连结构和标准化共同应用于GRU模型时，和直连后置结构相比，直连前置结构可以防止直连结构中增加额外的非线性计算，使得梯度的反向传播过程中存在与输入无关的常数项，防止中间层梯度消失导致模型整体无法得到优化，降低了梯度传播的难度，因此模型更容易得到优化.

4 实验设计

为验证本文提出的基于GRU的缩放残差前置模型的有效性，下文将分别针对语音识别任务和语言模型为例分别进行验证.为保证实验的公平性，下文中的实验将分别使用标准GRU模块构建基线模型，仅使用前文所述的改进GRU模块进行替换，保持其他因素不变.其中，标准GRU模型由层标准化和GRU组成，改进GRU为恒等残差连接、高速公路连接、缩放残差连接3种直连结构和未使用层标准化、直连前置结构、直连后置结构3种连接方式进行组合，共包含9种改良GRU模块，简化命名规则如表1所示.

表1 改良GRU模块命名

4.1 语音识别实验设计

语音识别任务是在给定音频的情况下判断该音频对应的本文信息，常使用字符错误率(Character Error Rate，CER)作为模型的评价指标.本文选择DeepSpeech2(DS2)作为基线模型构建声学模型在THCHS-30数据集上进行语音识别实验[18，19].DS2主要由CNN-GRU-FC-CTC构成，以80维fbank特征作为模型输入.

为防止过拟合，本文使用提前终止策略选择模型.若6次迭代内模型在验证集上的CER停止下降，则终止训练，并确定当前模型为最优模型，进而使用该最优模型在测试集上进行测试.

4.2 语音识别实验结果

对于使用标准GRU模块的DS2模型，设置层数分别为2、3、4层，其他结构均保持不变，实验结果如表2所示.由此看出，随着模型深度增加，参数量上升，性能呈现先上升后下降趋势，退化现象明显.当层数为3时，性能达到最优，词错误率为8.96%.层标准化尽管在一定程度上解决了梯度爆炸和梯度消失现象，但是随着模型深度增加，无法抑制退化现象的发生.

表2 标准GRU模块实验结果

为进一步验证不同直连结构以及不同连接方式对模型收敛的影响，本文以标准4层DS2模型(GRU L4)为基线模型，分别对恒等残差连接、高速公路连接以及本文提出的缩放残差连接进行实验.试验结果表3所示.

表3 改进GRU模块实验结果

对于使用改进GRU模块的DS2模型，Scale before GRU的表现最佳，和基线模型相比测试集错误率降低1.60%，相对下降16.10%，提升明显.缩放残差连接GRU模块的CER变化曲线如图5所示，与未添加直连结构的基线模型相比，添加缩放残差连接后的GRU模型收敛速度明显提升.与使用恒等残差连接的DS2模型相比，参数量增加768(总参数量的0.02%)，尽管该结构增加了额外的参数，远低于高速公路连接增加的参数量197376(总参数量的5.81%).

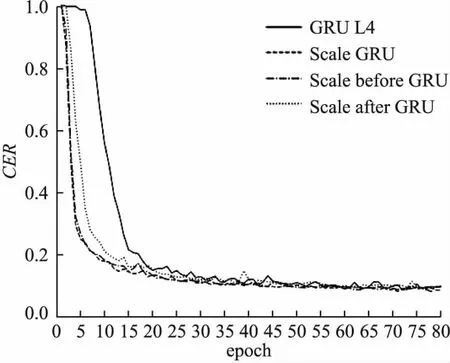
图5 缩放残差连接GRU模块CER变化曲线

使用恒等残差连接时，残差分支逐渐累积，模型各层输出范围随层数的增加逐渐扩大，使得GRU内部的更新门与重置门更容易接近饱和，进一步增加模型内部梯度消失的可能性，因此在九种改进GRU模块中性能最差.

由于高速公路连接使用额外的门控单元控制直连结构的信息流动，一定程度限制了模型输出的取值范围，因此将其应用于使用饱和激活函数的GRU模型时，可以取得比恒等残差连接更好的效果.但是其门控机制由于使用非线性激活函数，因此参数量上升明显，且其梯度传播过程受到阻碍，其性能劣于添加缩放残差连接的模型.

无论何种直连结构，当与LN联合使用时，直连前置结构模型由于消除了直连结构中的非线性计算，降低梯度传播的难度，因此效果均明显优于直连后置结构.该差异在恒等残差连接和缩放残差连接更为明显，但是在高速公路连接中，无论何种连接方式，由于高速连接本身已经在直连结构中添加了非线性的门控机制，因此连接方式不会对高速公路连接产生明显影响.

4.3 语言模型实验设计

语言模型任务是在给定文本的情况下判断该文本信息的合理性，在自然语言处理中得到广泛应用，常使用困惑度(Perplexity，PPL)作为评估指标，在测试集上PPL越低，模型性能越好[20].本文选择DGRU作为基线模型构建语言模型在数据集Penn Tree bank(PTB)进行实验[21].DGRU主要由Embedding-GRU-FC组成，输入的字符将通过Embedding 转换为词向量，并使用单向GRU提取序列信息并预测后续字符的概率分布[21].

4.4 语言模型实验结果

对于使用标准GRU模块的DGRU模型，设置层数分别为4、6、8层，其他结构均保持不变，实验结果如表4所示.和4层的模型相比，随着模型深度增加，模型参数量迅速上升，性能呈现下降趋势，模型无法得到有效收敛，退化现象明显.当层数为4时，性能达到最优，困惑度为231.82.

表4 标准GRU模块实验结果

为进一步验证不同直连结构以及不同连接方式对模型收敛的影响，本文以标准8层DGRU模型(GRU L8)为基线模型，分别对恒等残差连接、高速公路连接以及本文提出的缩放残差连接进行实验，试验结果表5所示.

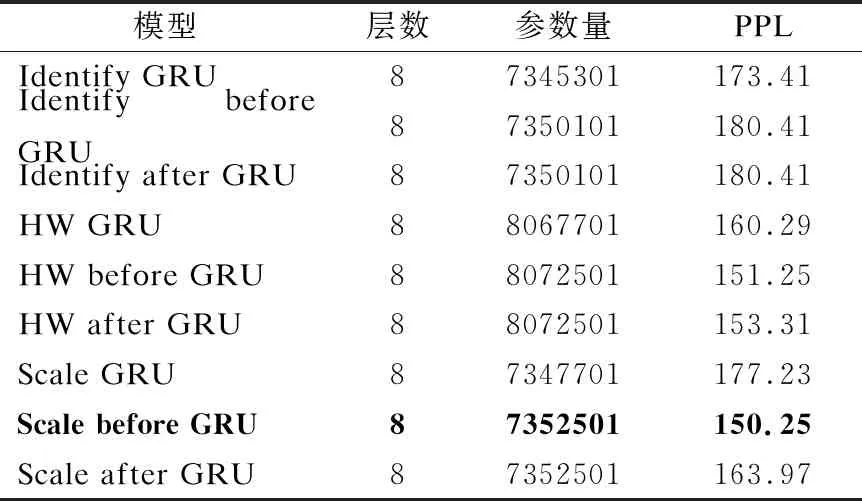
表5 改进GRU模块实验结果

对于使用改进GRU模块的DGRU模型，该实验不同改良模型的性能变化和前文中的语音识别模型实验结果相似.在多种改良模型中Scale before GRU的表现最佳，和基线模型相比测试集困惑度降低402.02，相对下降72.79%，效果显著提升.缩放残差连接GRU模块的CER变化曲线如图6所示，与未添加直连结构的基线模型GRU L8相比，添加缩放残差连接后的GRU模型收敛速度明显提升，在第1次迭代结束后即可得到很好的表现，之后模型以平稳趋势得到优化.与使用恒等残差连接的DGRU模型相比，参数量增加2400(总参数量的0.03%)，尽管该结构增加了额外的参数，远低于高速公路连接增加的参数量722400(总参数量的9.83%).

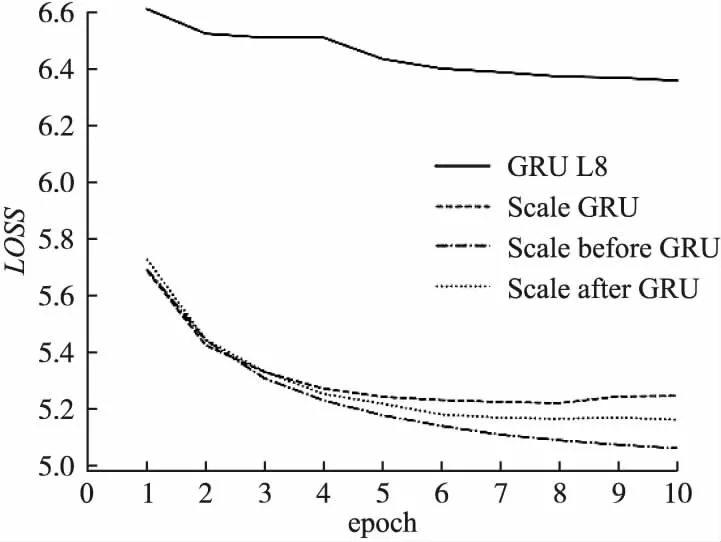
图6 缩放残差连接GRU模块LOSS变化曲线

对于使用相同直连结构的模型，直连前置结构的性能均明显高于直连后置结构.且恒等残差连接在不同直连结构中效果最差.高速公路连接取得了和缩放残差连接相似的效果，但是其参数量将会明显提升.

5 结束语

针对GRU模型深度增加伴随的梯度消失和退化现象，本文提出一种基于缩放残差前置结构的GRU模型.该模型利用线性缩放结构筛选层间信息，通过增加少量参数换取线性转换，进而实现信息与梯度的有效传递.通过和层标准化联合使用构建直连前置结构防止直连结构中增加非线性计算.最后，针对语音识别任务和语言模型任务验证算法有效性，结果表明，基于缩放残差前置结构的GRU模型可有效缓解梯度消失与退化现象，进而提高模型收敛速度及性能.