基于聚合多阶邻域信息的细化方法的多粒度网络表示学习

赵 姝，刘梦婷，杜紫维，宋文超，韩光洁

1(计算智能与信号处理教育部重点实验室，合肥 230601)

2(安徽大学 计算机科学与技术学院，合肥 230601)

3(安徽省信息材料与智能传感重点实验室，合肥 230601)

4(北京智创信安信息科技有限公司，北京 100080)

5(河海大学 物联网工程学院，江苏 常州 213022)

1 引 言

从宏观的社交网络到微观的蛋白质网络，网络已成为抽象和建模复杂系统的重要工具，在我们的生活中无处不在.如何挖掘隐藏在网络中的信息有着重要价值.近年来，网络表示学习作为网络分析的一种方法，受到极大的关注.网络表示学习，又称网络嵌入，旨在将网络中的节点映射成低维稠密的向量，同时保留网络的固有特征.学到的节点表示可以作为机器学习算法的输入，用于处理社区发现、节点分类、链路预测等下游任务，对挖掘网络的潜在信息有着重要作用.

为获得有效的节点表示，研究者们已提出各种网络表示学习方法.DeepWalk[1]、Node2vec[2]将随机游走和浅层神经网络相结合得到节点向量.HuGE[3]利用混合属性启发式随机游走捕获节点特征.NetMF[4]、ProNE[5]、eNetMF[6]基于矩阵分解的技术得到表示向量.随着图神经网络的发展，GCN[7]、MAGCN[8]等基于深度学习的方法被提出，这类方法通过半监督的方式学习节点表示，在训练过程中需要利用标签信息.虽然上述方法已经取得了不错的效果，但是它们只考虑了单一粒度下网络的结构信息，忽略了网络的多粒度特征.然而，现有的复杂网络大多呈现多粒度的结构[9]，如社交网络、引文网络、蛋白质网络等.

最近，多粒度网络表示学习方法因其可以保留网络的多粒度特征，从不同粒度上分析网络的特性，而受到越来越多的关注.它们利用一种统一的框架得到节点表示.具体地，主要经过网络粗化和网络细化两个阶段.网络粗化阶段，通过设计节点合并策略，将网络中具有相似特征(一阶相似性、二阶相似性、社团结构)的节点合并生成超点，构成粗粒度网络.通过粗化阶段可以缩小原始网络的规模，同时，由于粗粒度节点与细粒度节点之间的对应关系，可以将粗粒度网络的表示作为原始网络的近似表示.迭代粗化过程还可以获得网络的多粒度结构.

网络细化阶段旨在保留粗化过程中获得的多粒度结构，将粗粒度空间的节点表示细化回原始网络，得到原始网络的节点向量.现有的细化方法主要分为3大类：第1类方法，如图1(a)所示，通过在不同粒度网络上运用已有的网络表示学习方法，并利用拼接操作融合不同粒度的节点表示以得到最终的嵌入向量.但这类方法需要学习每一粒度网络的节点向量，所需的时间复杂度高，同时采用直接拼接的方法，会造成信息的冗余；第2类方法，如图1(b)所示，通过继承粗粒度网络的节点表示，将其作为细粒度网络的初始嵌入值，再利用现有的网络嵌入方法进一步对细粒度网络的节点表示进行更新.重复这一过程，直到获得原始网络的节点表示.本质上，与基于拼接的方法类似，该类方法仍需要学习每一粒度网络的节点表示，所需的时间开销大；第3类方法，如图1(c)所示，与第2类方法类似，采用继承的思想进行细化操作.但对细粒度网络的嵌入向量进行更新时，不再需要学习过程，仅使用在最粗粒度上训练过的图卷积网络[7]模型，此时节点更新过程可简单的看成几个矩阵相乘.虽然这种方法减少了学习不同粒度网络表示的时间，但受到GCN模型的影响，在更新细粒度网络节点表示时，通常只能聚合2-3阶的邻域信息，无法聚合高阶邻域信息.

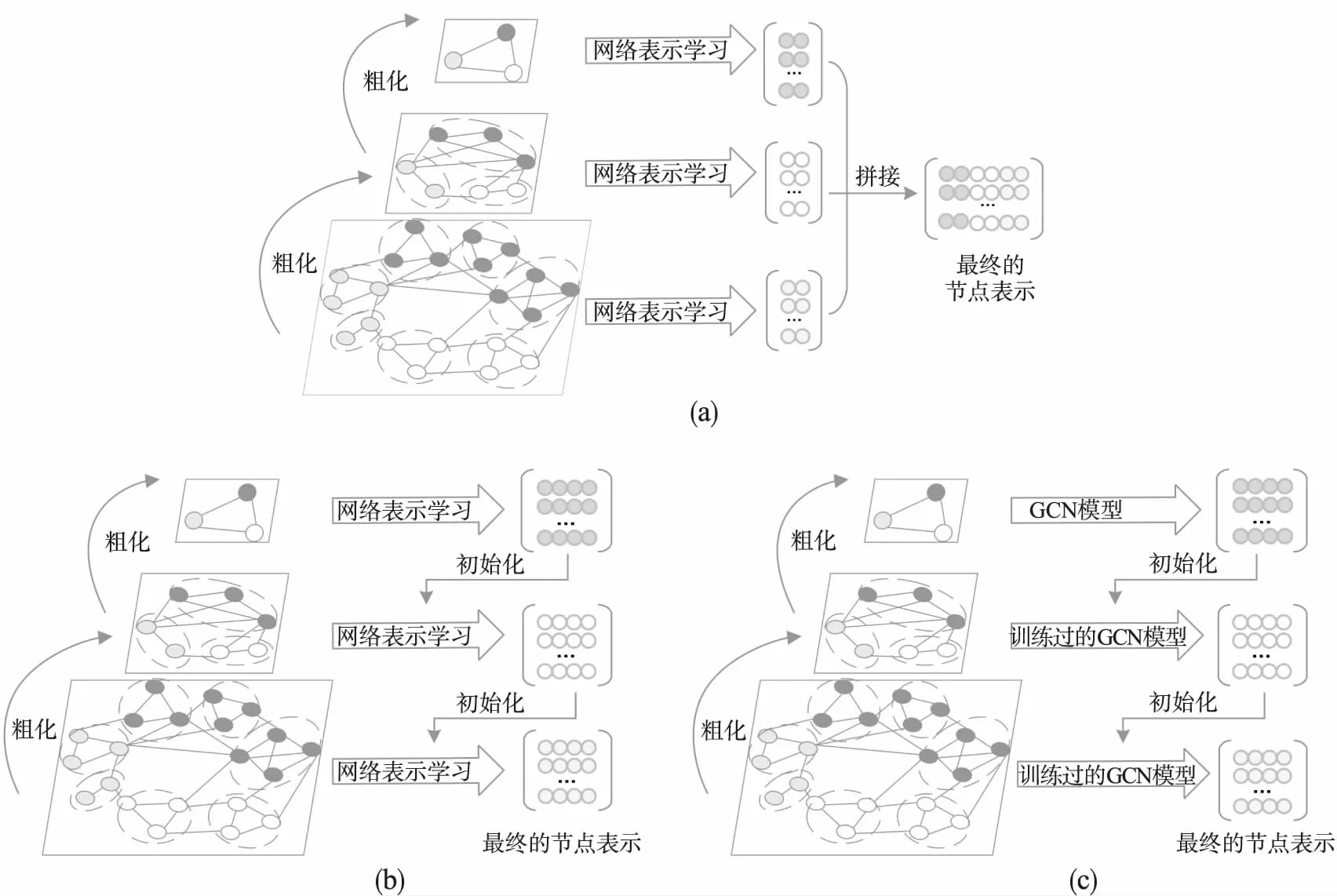
图1 多粒度网络表示学习

因此，本文提出一种基于聚合多阶邻域信息的细化方法的多粒度网络表示学习方法.具体地，对于粗化后得到的多粒度网络，首先利用已有的网络表示学习方法学习最粗粒度网络的节点表示，将其作为伪标签训练细化模型，避免再次学习每一粒度网络的节点向量；然后利用继承的思想，将粗粒度得到的节点表示投影到细粒度网络，使构成同一超点的节点表示相同，并融合细粒度网络的结构信息得到细粒度网络的初始嵌入；最后，通过聚合节点的高阶邻域信息以更新每一粒度网络的表示，重复这一过程，直到得到原始网络的节点表示.

本文贡献总结如下：

1)基于多粒度网络表示学习的框架，提出一种新的细化方法，利用谱卷积技术，在逐层更新细粒度网络的节点表示时，可以聚合多阶邻域信息.

2)利用拉普拉斯矩阵的特征值定义广义的位置嵌入矩阵，作为辅助信息，在网络细化时可以进一步保留细粒度网络的结构信息.

3)本文在3个公共数据集上进行节点分类的实验，证明NRAM(Network Refinement based on Aggregating Multi-neighboring information)方法与其他一系列最先进的方法相比在节点分类任务上的优越性.

2 相关工作

本文从单粒度网络表示学习方法和多粒度网络表示学习方法两个角度介绍现有的网络表示学习方法.

2.1 单粒度网络表示学习方法

早期的网络表示学习方法，通过构建随机游走序列得到节点表示，如DeepWalk、Node2vec受Word2vec的影响，构建随机游走序列并结合浅层神经网络以得到节点表示；CNBE[10]、CARE[11]在设计随机游走策略时，进一步考虑社团结构的影响；HuGE[3]基于启发式的策略设计随机游走序列.还有一些方法利用矩阵分解的技术得到节点表示，如ProNE[5]、GraRep[12]、Lemane[13]等.但这些方法都是浅层的，无法捕获高度非线性的网络结构.因此，SDNE[14]、 DVNE[15]、NetRA[16]等方法采用深度学习的方式获得网络中节点的潜在表示.同时，随着图神经网络技术的发展，GCN[7]、GraphSAGE[17]等基于GNN的方法被提出，然而这些方法都需要利用节点的标签信息.上述方法都属于单粒度网络表示学习方法，在学习节点表示的过程中只利用了单一粒度即原始网络的拓扑结构，无法保留网络的多粒度特征.

2.2 多粒度网络表示学习方法

该类方法大多利用统一的框架，通过递归的调用粗化方法来得到原始网络的多粒度结构，获得单粒度网络无法得到的多粒度网络特征.并利用细化方法以保留该多粒度特征，得到原始网络的节点表示.根据其细化方法的不同主要可以分为3类：1)HSRL[18]、ACE[19]这类方法通过学习每一粒度网络的节点表示，并利用拼接的方式得到最终的节点表示，所需的时间复杂度高.LouvainNE[20]也利用了拼接的思想，但是对于每一粒度的表示仅利用随机嵌入的方法，虽然可以快速得到节点表示，但牺牲了节点表示的质量；2)HARP[21]、HCNE[22]利用继承的思想，对于粗化阶段得到的多粒度网络，从最粗粒度的网络开始，通过将粗粒度网络的表示继承下来作为细粒度网络的初始嵌入，并利用现有的网络表示学习的方法重新学习细粒度网络的节点表示.与第一类方法类似，该类方法也需要利用现有的网络表示学习方法重新学习每一粒度网络的表示，时间开销大；3)HGNS[23]、MILE[24]通过不同的粗化策略压缩网络的规模，构建多粒度网络；细化阶段仍利用继承的思想，但不需要再重新学习每一粒度网络的节点表示，仅利用最粗粒度网络上训练的图卷积网络逐层细化更新得到节点的表示.受GCN模型的限制，该类方法在逐层更新细粒度网络的节点表示时，无法利用节点的高阶邻域信息.

3 问题定义

下面给出本文所提问题的定义及使用的符号定义.

定义1.网络.G=(V，E，A)表示网络，其中V={v1，v2，…，vn}表示构成网络的n个节点的集合，E表示网络中存在的所有边的集合，A∈Rn×n表示网络的邻接矩阵，用于定义节点间的连接关系.

定义2.网络表示学习.给定网络G=(V，E，A)，通过学习映射函数：f：G→Rn×d，其中d≪n，可以得到保留网络重要特征的节点向量Z，zi表示节点vi的低维向量表示.

定义3.网络粗化.给定网络G=(V，E，A)，令G0=G，通过定义网络粗化方法Coarsen：Gi→Gi+1，|Vi+1|<|Vi|，i=0，1，…,k-1，k表示多粒度网络的粒度数，即粗化层数，Gi+1是比Gi粒度更粗的网络，迭代的将不同粒度中结构相似的节点合并成超点，构造出规模逐渐减小的多粒度网络G0，G1，…，Gk.

定义4.网络细化.利用网络粗化阶段得到的多粒度网络G0，Gi，…，Gk，网络细化旨在通过学习每一粒度网络的表示Zi←f(Gi)，i=0，…，k，将粗粒度空间的节点表示细化回原始网络，最终得到原始网络的节点向量Z0.

定义5.多粒度网络表示学习.多粒度网络表示学习包括网络粗化和网络细化两个阶段.给定网络G=(V，E，A)，先利用网络粗化方法构造多粒度网络G0，G1，…，Gk，其中Gk表示最粗粒度的网络.再利用细化方法，得到保留网络多粒度特征的原始网络的节点表示Z0.

4 算法描述

为保留网络的多粒度结构，将粗粒度空间的节点表示细化回原始网络，本文提出基于聚合多阶邻域信息的细化方法的多粒度网络表示学习.主要包含两个模块，基于社团压缩的网络粗化模块和基于聚合多阶邻域信息的网络细化模块.通过粗化模块可以捕获网络的多粒度结构，并利用网络细化模块保留该多粒度结构，得到原始网络的节点表示.

4.1 基于社团压缩的网络粗化

给定原始网络G=(V，E，A)，粗化阶段的目的是通过粗化方法迭代地构造出规模逐渐减小的网络G1，…，Gk，获得网络的多粒度结构.具体地，以Gi到Gi+1的粗化过程为例.首先，利用社团划分算法将Gi划分成多个不重叠的社团，本文选择基于模块度的社团划分算法Louvain[25]算法；然后，将每个社团的节点合并构成粗粒度网络Gi+1中的超节点.为了保留粗化过程中，粗粒度网络和细粒度网络中节点的对应关系，即Gi中的节点和Gi+1中超节点的对应关系，定义匹配矩阵M|Vi|×|Vi+1|，其中每个元素Mjk可定义为：

(1)

对于超点间的连边情况，需要考虑Gi的结构.如果构成不同超点的社团中的节点有连边，则粗粒度网络Gi+1中对应的超点间也存在一条连边.如图2所示，通过社团压缩的方式，可以将Gi压缩成3个不重叠的社团，构成粗粒度网络Gi+1的节点集{vABC，vDE，vF}.由于构成超节点vDE，vF的节点vD和vF间存在连边，则超点vDE，vF间存在连边.通过构建Gi+1的邻接矩阵Ai+1可以保留该关系：

图2 多粒度网络细化过程

(2)

重复这一过程，得到规模逐渐变小的网络G1，…，Gk，其中Gi揭示了原始网络不同粒度的拓扑信息.

4.2 基于聚合多阶邻域信息的网络细化

网络细化旨在通过将粗粒度空间的节点表示细化回原始网络，以保留粗化阶段获得的多粒度结构G1，…，Gk，得到原始网络的节点表示Z0.

为了解决这一问题，本文首先讨论如何从Gi+1细化到Gi.一旦解决这个问题，就可以迭代的将该方法运用到相邻的不同粒度的网络上，最终得到原始网络的节点向量Z0.具体的，给定网络Gi，对应的粗粒度网络Gi+1和粗粒度网络的节点表示Zi+1，如何推断出Gi的节点表示Zi.以图2为例，显示粗粒度网络Gi+1到细粒度网络Gi的细化过程.

首先，通过投影的方式，继承粗粒度网络Gi+1的特征，Gi中每个节点的初始嵌入值等于对应的Gi+1中超节点的嵌入，如图2所示，Gi中的节点vA，vB和vC与其构成的Gi+1中的超点vABC的表示相同，同理可推导出vD，vE和vF的表示.再融合细粒度网络Gi的结构信息，得到细粒度网络的初始表示：

Zi=Project(Zi+1，Gi)⊕Xi

(3)

Project(Zi+1，Gi)=Mi，i+1×Zi+1

(4)

其中Project(·)表示投影操作，⊕表示拼接操作，通过该操作可以保留粗粒度网络Gi+1的特征.同时为了更好地利用细粒度网络的结构信息，对于每一粒度的网络，基于结构信息利用网络的拉普拉斯矩阵定义广义位置嵌入矩阵[26]Xi.具体地，先对归一化的图拉普拉斯矩阵L进行特征分解：

L=D-A=I-D-1/2AD-1/2=UΛUT

(5)

其中D表示网络的度矩阵，Λ是n个特征值构成的对角矩阵，U表示对应的特征向量，取U中前top-k的特征向量的值定义为广义的位置嵌入矩阵Xi.

(6)

然后，为了进一步优化Zi，引入谱卷积模型[27]来更新节点的表示.该模型利用改进的马尔可夫扩散核，通过捕获每个节点的局部和全局上下文信息，可以聚合节点高阶邻域的特征.具体原理如下：

(7)

(8)

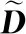
基于上述的计算步骤，可以推导出不同粒度的网络表示，最终得到保留网络多粒度特征的原始网络的节点表示Z0.

为了避免在每一粒度网络上重新训练模型，同时更好地得到模型的初始化参数.本文仅利用最粗粒度网络Gk的信息来训练谱卷积模型，通过定义均方误差损失训练模型：

Zk=Emd(Gk)

(9)

(10)

其中Emd(·)的选择是灵活的，可以选择现有的基于结构的网络表示学习方法.由于最粗粒度节点和最细粒度节点之间的 关系，Zk可以作为原始网络中节点的近似表示，并作为细化过程的初始值.因此，在细化过程中将最粗粒度得到的节点表示作为标签训练谱卷积模型.在不同粒度网络的细化过程中，使用参数共享的思想，仅利用在最粗粒度网络上训练好的模型来更新节点表示，不再单独训练模型，此时每两个粒度间信息的转换只需要利用简单的矩阵相乘就可以实现，减少了模型训练的时间.同时相较于随机初始化参数的方法，该方法可以得到更好地初始化参数.NRAM的具体实现过程如算法1所示.

算法1.NRAM

输入：原始网络G；粒化层数k；节点嵌入的维度d；网络粗化方法Coarsen(·)；任意的网络表示学习方法Emd(·)；谱卷积模型H(A，X)

输出：G的节点表示Z0∈Rn×d

1.for i=0，…，k-1 do

2.Gi+1←Coarsen(Gi)

3.End

4.Zk=Emd(Gk)

7.for j=k-1，…，0 do

8.Project(Zj+1，Gj)=Mj，j+1×Zj+1

10.Zj=Project(Zj+1，Gj)⊕Xj

11.Zj=H(Aj，Zj)

12.End

13.ReturnZ0

算法1中，第1-3行利用网络粗化方法得到多粒度网络，第4-6行通过利用最粗粒度网络的表示训练谱卷积模型.第8-10行在继承粗粒度节点信息的同时，进一步融合细粒度网络的结构信息得到细粒度网络的初始嵌入.第11行通过聚合节点的高阶邻域信息更新细粒度网络的节点表示.逐层细化，最终得到原始网络的节点表示.

5 实验分析

5.1 数据集

为了验证NRAM的有效性，本文在3个公共数据集上进行实验，数据集的具体信息如表1所示.

表1 数据集

Cora[28]是由2708篇与机器学习相关的论文和其之间的引用关系构成的引文网络，每篇论文根据其所属的研究领域被分为7个类别.

DBLP[29]是由13404篇论文和其引用关系构成的引文网络，包含39861条边，每篇论文根据其不同的研究领域可以被划分成4个类别.

Pubmed[28]是医学数据库中一组与糖尿病相关的文章构成的引文网络，每篇论文根据其所属的糖尿病类型可以被划分成3个类别.

5.2 对比算法

为验证NRAM算法的有效性，本文选取了具有代表性的网络表示学习方法作为基线方法.主要分为以下3类：

1)单粒度网络表示学习方法

DeepWalk[1]利用随机游走策略生成节点序列，并利用Word2vec学习节点的表示向量.

GraRep[12]通过矩阵分解的方法学习节点的k阶关系表示以生成节点的潜在表示.

ProNE[5]通过稀疏矩阵分解有效地初始化网络表示，并在谱空间中传播表示，以获得增强的节点表示.

HuGE[3]是一种熵驱动的网络嵌入方法，利用混合属性启发式随机游走来捕获节点特征.

2)基于拼接的细化方法的多粒度网络表示学习方法

HSRL[18]采用社团压缩的方法构建网络的多粒度结构，学习不同粒度网络的节点表示，通过拼接的操作以得到网络的潜在节点表示.

ACE[19]采用基于蚁群算法的粗化方法，构建多粒度网络，并将不同粒度的网络表示拼接起来并降维得到最终的表示向量.

LouvainNE[20]通过构建层次树的方法保留网络的多粒度结构，将不同粒度上获得的单个节点表示拼接以学习最终的嵌入向量.

3)基于继承的细化方法的多粒度网络表示学习方法

HARP[21]递归地使用两种坍塌方案，边坍塌和星坍塌，将输入网络粗化成一系列小网络.从最粗粒度网络开始，将粗粒度网络学到的表示作为细粒度网络的初始化，迭代的得到原始网络的表示.

MILE[24]使用混合匹配技术反复地将图合并成更小的图，并利用GCN[7]方法将最粗粒度学到的节点表示细化回原始网络.

5.3 参数设置与评价标准

本文所涉及实验方法的嵌入维度统一设置为128维.同时为了保证实验的公平性，对于对比算法中的多粒度表示学习方法，统一采用DeepWalk[1]方法作为最粗粒度网络的基本嵌入方法.对比算法中其它的相关参数设置依据相应论文中设置的值.为评估学到的节点表示的质量，本文使用节点分类作为下游任务，使用Micro-F1(Mi-F1)，Macro-F1(Ma-F1)作为评价指标.其定义如下：

(11)

(12)

其中TP、FP、FN分别表示真正例、假正例、假反例.N表示标签的类别数.Micro_F1可看做N个不同类别F1值的加权平均值，Macro_F1是所有类别F1值的算术平均值.

5.4 实验结果

为验证NRAM方法的有效性，本文使用节点分类作为下游任务评估网络表示学习质量.与之前的研究相似，本文使用Micro_F1和Macro_F1作为衡量节点分类性能指标.随机抽取不同训练率的标记样本用来训练SVM分类器，其余节点用于测试.每个实验独立执行10次，实验结果如表2-表4所示，其中k表示网络粗化的层数，由于空间限制，对于多粒度网络表示学习方法仅显示粗化层数为1、2、3时的结果. 同时由于HARP[21]、ACE[19]、LouvainNE[20]等方法直接采用阈值来设置粗化终点，其粗化层数不可控制，因此对于该方法，仅显示最终的表示向量；HSRL[18]是基于拼接的方法，因此为保证嵌入维度相同，仅显示粗化层数为1、3时结果.每列中的最好的结果用粗体突出显示.从表2-表4中，可以得到以下结论：

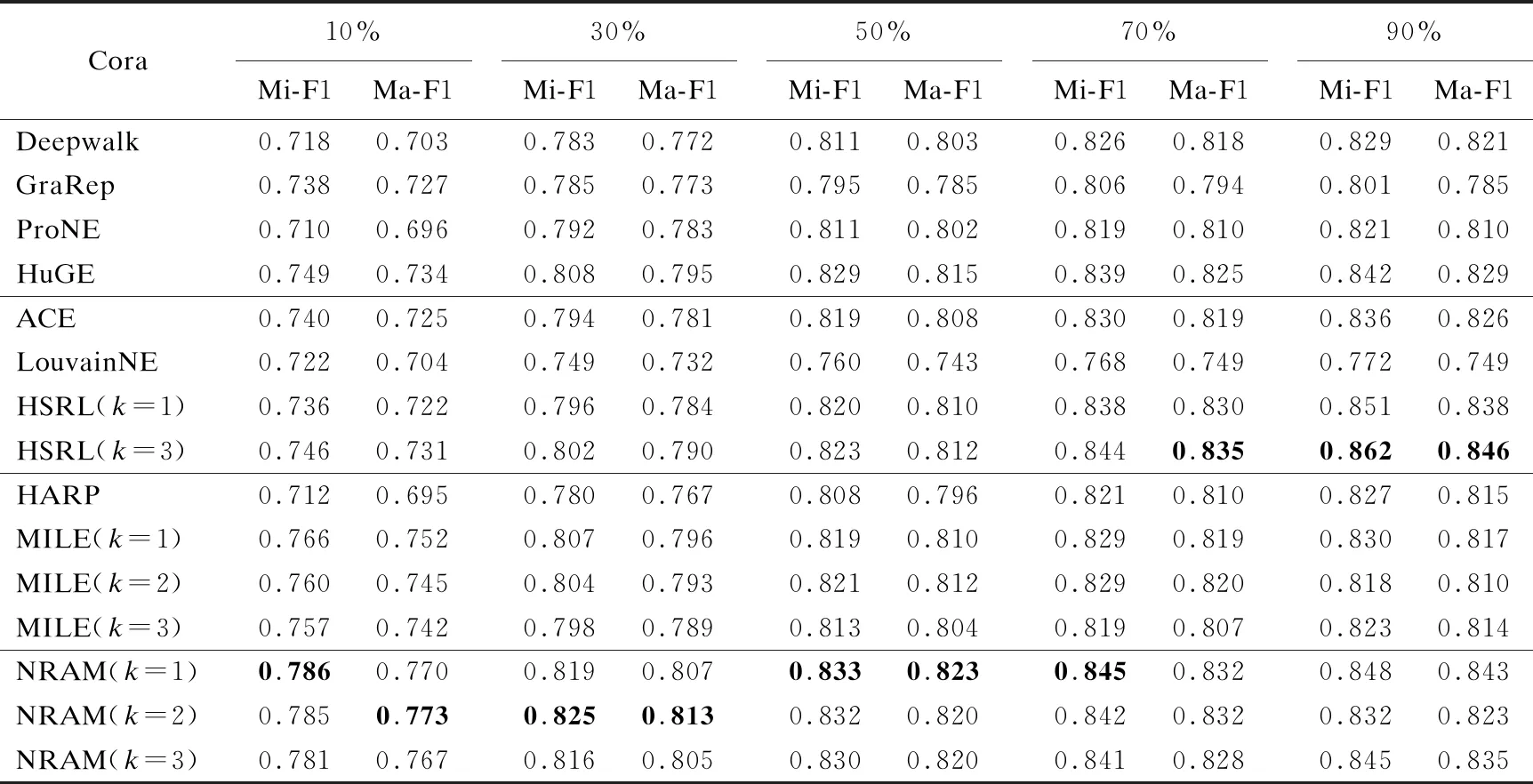
表2 Cora数据集上节点分类的结果

表3 DBLP数据集上节点分类的结果

表4 Pubmed数据集上节点分类的结果

首先，从表2-表4中可以观察到相对于HuGE[3]等单粒度的网络表示学习方法相比，NRAM方法其节点分类的结果有明显的提高，进一步证明了保留网络的多粒度信息对于节点表示的重要性，同时也可以反映出本文的方法可以更好地捕获网络的多粒度结构.其次，相较于多粒度网络表示的方法，NRAM的效果也有提升.HARP使用边坍塌和星坍塌的粗化方法，属于不同社区的节点可能会被合并，不利于细化过程中得到的初始嵌入.LouvainNE的方法使用随机嵌入的方法学习节点表示，在减少学习时间的同时损失了节点表示的质量.与MILE[24]相比，NRAM在逐层细化时可以聚合高阶邻域的信息，同时利用了细粒度网络的结构信息.虽然与HSRL[21]相比，在测试集比率为70%和90%上Cora数据集的结果差于HSRL的结果，但相较与HSRL需要学习每一粒度的节点表示相比，NRAM仅在最粗层学习节点的表示向量，所需的时间开销小.

5.5 消融分析

本节将进行消融实验来验证NRAM的细化方法的有效性.本文设计了NRAM方法的3种变体方法，仅改变NRAM的细化方法，即NRAM-gcn，NRAM-contate和NRAM-nox.NRAM-gcn方法在细化过程中使用GCN替代谱卷积模型，同时在逐层细化时，不拼接广义的位置嵌入矩阵.NRAM-contate方法直接使用拼接的方法进行网络细化，学习每一粒度网络的节点表示并拼接得到最终的表示向量.NRAM-nox在细化过程中去掉每层拼接的广义位置嵌入矩阵.为了比较的公平性，使用Deepwalk分别学习NRAM-nox、NRAM-gcn最粗粒度和NRAM-contate中每一粒度网络的节点表示.表5和表6展现了粗化层数为3，训练率分别为10%，30%和50%时节点分类任务上的性能.从表5和表6中可以看到，相较于NRAM-gcn直接使用GCN模型更新节点的表示，NRAM细化方法的效果更好，NRAM在细化更新节点表示时，保留了细粒度网络的高阶信息，并且相较于传统的GNN方法，仅在聚合节点信息时利用网络的局部邻域信息来确定聚合的邻居节点.本文利用拉普拉斯矩阵的特征值定义广义的位置嵌入矩阵进一步考虑了细粒度网络的结构信息.同时，相较于NRAM-contate采用直接拼接的方法得到网络表示，NRAM的细化方法的效果更好，采用拼接的方法随着网络粗化层数的增多会造成信息的冗余而降低节点表示的质量.

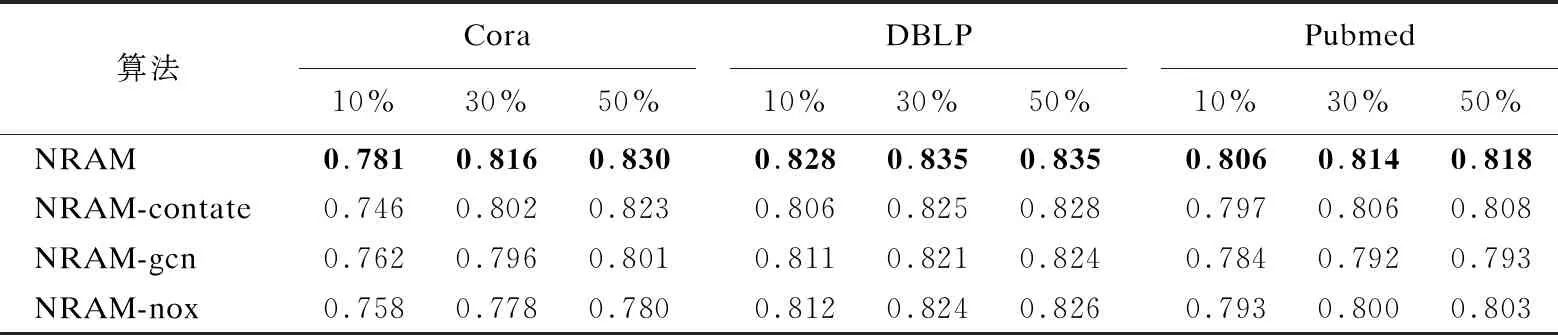
表5 NRAM和其变体方法的Micro-F1值

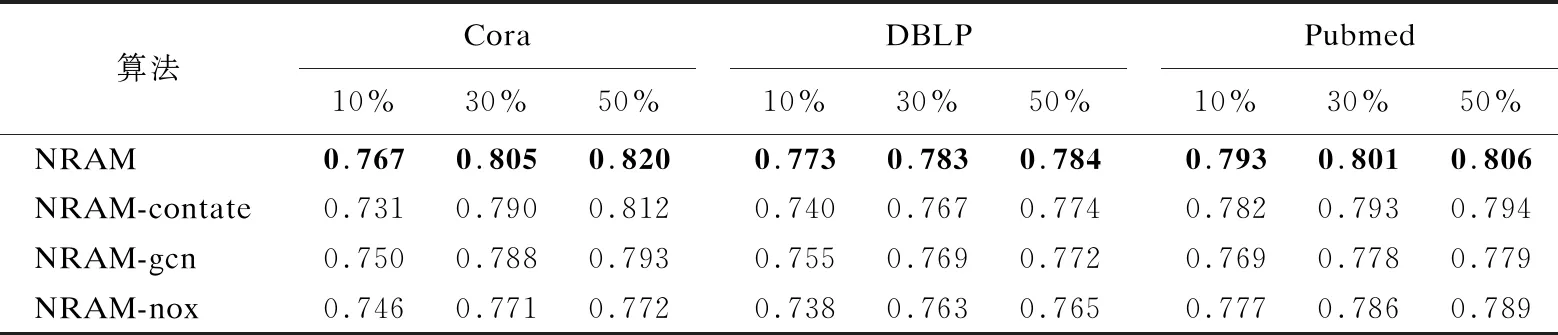
表6 NRAM和其变体方法的Macro-F1值

5.6 灵活性

本节将通过实验展示NRAM方法的灵活性，即在最粗的粒度网络上可以使用任何现有的基于结构的网络表示学习方法学习潜在的节点表示.这里选择两种网络表示学习方法GraRep[12]和ProNE[5]，如图3总结了训练率为20%时，在最粗粒度网络上采用不同网络表示学习方法的NRAM和原始网络表示学习方法的性能，本文选择GraRep和ProNE两种方法.在其他训练比率下，结果是相似的.从图3中可以看出，相较于原始的单粒度网络表示学习方法，NARM在3个数据集的节点分类任务上获得更高的Micro_F1和Macro_F1分数，这表明NARM可以更有效地保留网络的结构信息.

图3 NRAM在最粗粒度网络上使用不同网络嵌入方法的节点分类性能

6 结 论

网络表示学习对网络分析有着重要作用，如何更好地挖掘和保留网络的多粒度特征在现实生活中有着重要价值.本文基于聚合多阶邻居信息的细化方法提出一种多粒度网络学习方法.对于粗化后的多粒度网络，从最粗粒度网络开始，通过将粗粒度网络的表示投影到细粒度网络，并融合细粒度网络的结构信息得到细粒度网络的初始嵌入值；再利用节点的高阶邻域信息去更新细粒度网络的表示，逐层的将粗粒度空间的节点表示细化回原始网络，得到原始网络的节点向量.在3个公共数据集上节点分类的结果验证了NARM的有效性.