基于机动法的等边三角形计算截面弯矩影响线

梁丽浩

(泰山科技学院建筑工程学院，山东 泰安271000)

一般的工程结构往往同时承受固定荷载和移动荷载的共同作用，例如桥梁承受汽车、行人等移动荷载的作用，在车间内的吊车梁承受吊车移动荷载的作用。在移动荷载作用下，随着荷载位置的移动结构的反力和内力将发生变化[1]，因此在结构设计中,必须求出移动荷载作用下反力和内力的最大量值。解决这个问题的重要工具就是影响线，影响线是计算结构在移动荷载下内力、反力等量值的工具和手段[1]。在结构力学教材中，求解影响线的方法主要采用静力法和机动法[2]。

静力法[3]是根据静力平衡条件建立影响量方程，它是通过函数关系作出函数图求解影响线的方法，静力法求解简单的静定单跨梁或多跨梁所列的平衡方程比较简洁，计算也较简单，能够迅速建立方程，利用数学关系绘制函数图，即为所求影响线，但对于复杂静定多跨梁，根据静力平衡方程建立影响量方程求解函数关系式的过程中计算比较繁琐、步骤相对复杂，很难快速作出函数图求得影响线。

机动法[4]又称为虚功法，其作影响线的依据是理论力学中的虚位移原理[5]，即刚体体系在力系作用下处于平衡的必要和充分条件是：在任何微小的虚位移中，力系所作的虚功总和为零。因此，机动法求解影响线时需要根据虚位移原理，得到机构的几何位移图，但根据数学关系——三角函数往往无法求出精确的竖向位移值。应用等边三角形计算截面弯矩量值是近似求解，计算影响线的过程也是一种数学关系的应用[6]。该过程先根据机动法去掉相应约束代之反力，即杆件断开由铰结点连接，铰结点处添加一对力偶，去掉约束的结构变成机构，机构在反力偶的作用下发生微小位移，其中反力偶作用处铰结点连接的两个杆件发生单位角位移（忽略杆件变形）后利用等边三角形借助几何关系计算出反力偶作用处铰结点的竖向位移值，再利用几何关系计算出每个铰结点和自由端的竖向位移，从而求出对应的截面弯矩影响线[7]。

1 典型算例

1.1 单跨梁

求图1（a）所示静定单跨梁C 截面弯矩影响线[1-4]，其中梁长l，C 截面距支座A、支座B 距离分别为a、b，移动荷载F=1 作用在梁上。

（1） 结构变成机构，即去掉C 截面处约束，杆件断开变成铰结点连接，增加一对内力偶MC。

（2） 机构在内力偶MC的作用下杆件CA 和CB在C 铰结点处发生相对角位移，形成几何位移图，如图1（b）所示，图1（b）中杆件CA 沿A 端转动∠α，杆件CB 沿B 端转动∠β，根据三角形的外角=内角之和的数学关系，得∠AC1A1=∠α+∠β，再根据虚功原理应用——单位位移法，得到杆件CA 和CB 在铰结点C处产生的相对转动∠ACA1=∠α+∠β=1，然后把△AC1A1等效为等边三角形，即AA1=CA1=AC=a（AC忽略线弹性变化），由△BCC1∽△BAA1得CC1=ab/l。

（3） 绘制标有竖向位移值的几何位移图，即为单跨梁C 截面弯矩影响线（竖向位移在轴线以上为正，反之为负），如图1（c）所示。

图1 单跨梁跨中

1.2 多跨梁

（1） 求图2（a）中静定多跨梁跨中K 截面截面弯矩影响线[1-2]，其中各杆件长度如图所示，多跨梁受单位移动荷载P=1。

① 结构变成机构，即杆件AB 在K 截面处断开，去掉一个约束，杆件由铰结点连接，铰结点处添加一对内力偶Mk。

② 杆件KH 和杆件KE 在内力偶Mk的作用下首先在K 铰结点处产生相对角位移，根据虚功原理可知杆件KH 和KE 的相对角位移为单位位移，再利用杆件间的连动作用和杆件在滚轴支座支撑情况，最后得到各杆件在内力偶Mk的作用下运动后形成几何位移图，如图2（b），图中K 铰结点处的△K1BB1等效为等边三角形，BB1=K1B=KB=1（忽略杆件弹性变形），根据相似三角形关系，△AKK1∽△ABB1求得KK1=3/4，依次利用三角形相似比的关系△AHH1∽△AKK1∽△BEE1∽△EE1C∽△CFF1∽△FF1D∽△DGG1，求得HH1=1/4，EE1=9/4，FF1=9/2，GG1=9/4。

③ 绘制标有竖向位移值的几何位移图，即为静定多跨梁K 截面的弯矩影响线（竖向位移在轴线以上为正，反之为负），如图2（c）所示。

图2 多跨梁跨中K 截面

（2） 求图3（a）中多跨梁C 支座处截面弯矩影响线[12]，其中各杆件长度如图所示，多跨梁受单位移动荷载P=1。

① 结构变机构成为几何可变体系，即支座C 去掉一个约束代之内力，由复合支座变成链杆支座，增加一对内力偶MC。

② 机构在内力偶MC的作用下杆件CF 发生微小位移，再根据虚位移原理得到杆件CF 在C 处发生单位角位移，各杆件根据联动作用形成几何位移图，如图3（b），图中初始转动位置C 支座处的△CFF1等效为等边三角形，FF1=F1C=CF=2（忽略杆件弹性变形）；根据相似三角形，即△FF1D∽△DGG1，得GG1=1。

③ 绘制标有竖向位移值的几何位移图，即为多跨梁C 截面的弯矩影响线（竖向位移在轴线以上为正，反之为负），如图3（c）所示。

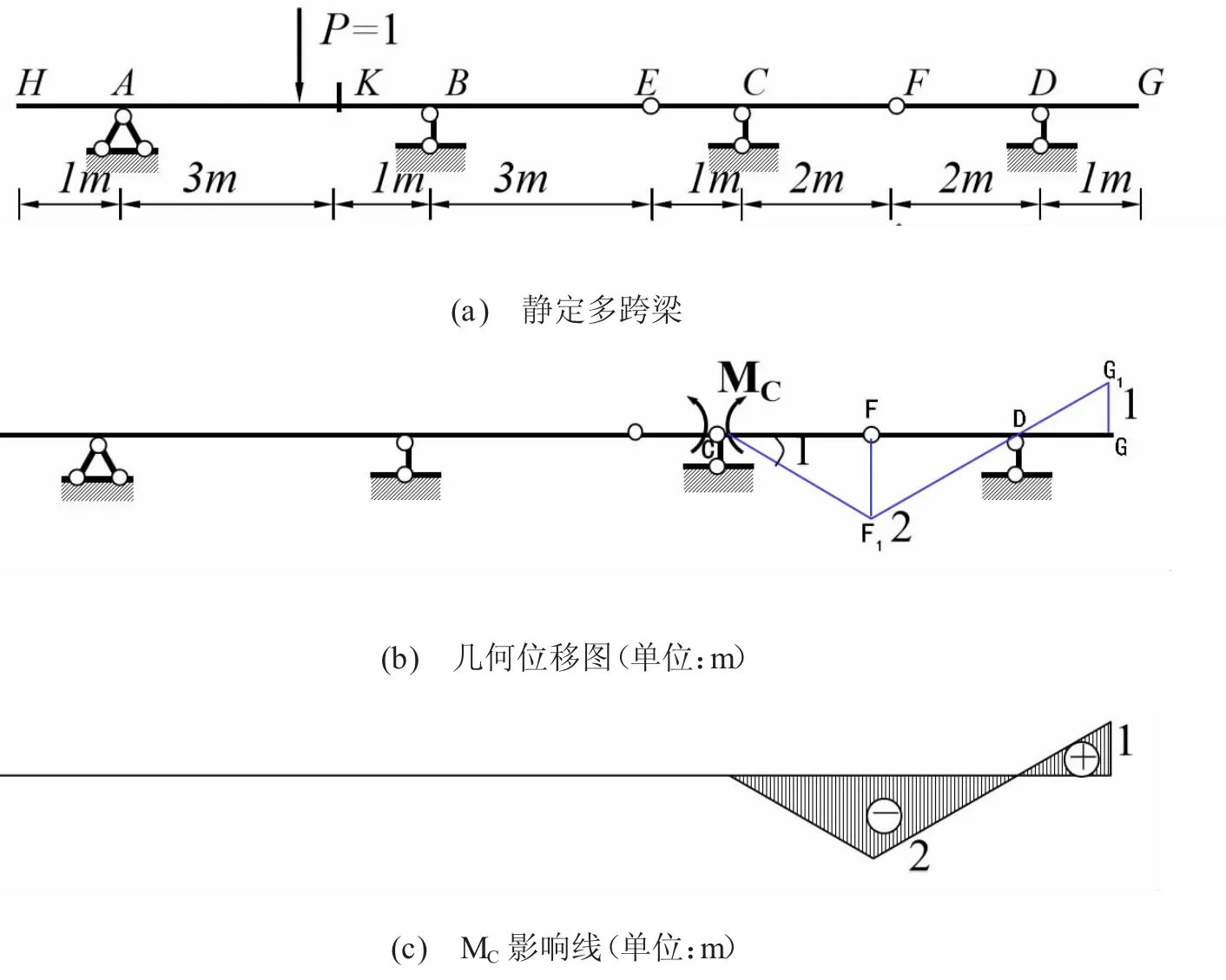
图3 多跨梁支座处C 截面

2 结论

本文应用“等边三角形”新思路计算静定单跨梁和多跨连续梁某截面弯矩影响线的过程主要分为三个步骤，首先去掉相应位置的约束代之内力偶，结构缺少约束变成机构（几何可变体系）；其次机构在内力偶的作用下发生微小位移形成几何位移图，在几何位移图中，初始位移处三角形等效为等边三角形，忽略杆件弹性变形确定三角形各边长，应用数学关系-相似三角形比例关系求出各三角形最高处的竖向位移值，最后标有竖向位移值的几何位移图，即得到截面弯矩影响线，其中影响量值正负号规定是轴线以上竖向位移为正，反之为负）[8-12]。三个典型算例表明，本方法适用于解决静定单跨梁和多跨连续梁某截面弯矩影响线的求解问题，与三角函数思想相比具有计算量小，高效快捷的优势。