某型卫星的随机振动仿真预测与试验验证

2022-12-05胡利鸿李杰伟

科学技术创新 2022年35期

胡利鸿，郭涛，谢鑫，李杰伟

（成都星时代宇航科技有限公司，四川成都 610041）

引言

卫星一般通过运载火箭发射到预定轨道上，而运载火箭在飞行过程中会承受复杂的振动载荷[1]，在研制过程中要进行复杂的力学环境试验[2-3]。随机振动是小型卫星发射过程中需要经历的重要力学环境，邓卫华等[4]从理论和试验两方面对比分析了随机振动环境和噪声环境的特点及环境试验的效果，得出随机振动试验比噪声试验更适合于小卫星的结论。

关于卫星振动的相关研究得到了国内外航天领域研究者的大量关注[5-8]。但对卫星的仿真和试验对比分析研究则相对较少，因此本研究采用随机响应分析法对自主研发的第四代AI 卫星的结构进行仿真分析，在得到结构的均方根加速度基础之上，对卫星样机进行随机振动试验验证，分析测得的卫星振动数据。进一步地，对仿真与试验结果进行对比分析探讨。

1 卫星有限元模型

卫星三维模型见图1，主要由卫星主体、太阳翼、分离底座、星上设备组成。

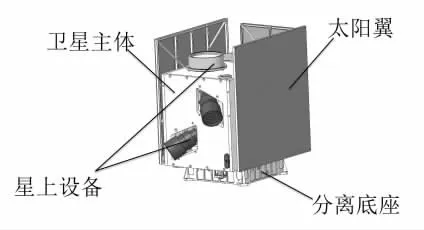
图1 卫星模型

基于三维模型，建立卫星的有限元模型，结构之间的螺接简化为固定约束，卫星上的设备采用质量点耦合到对应安装面的形式进行加载，并约束分离底座的四个安装角的六个自由度。

2 随机响应分析结果

将表1 所示的随机振动试验条件分别加载到卫星模型的三个方向上，并在有限元模型上建立如图2所示的11 个观测点（F1～F11），所建立的观测点与后续试验中加速度计安装位置保持一致。

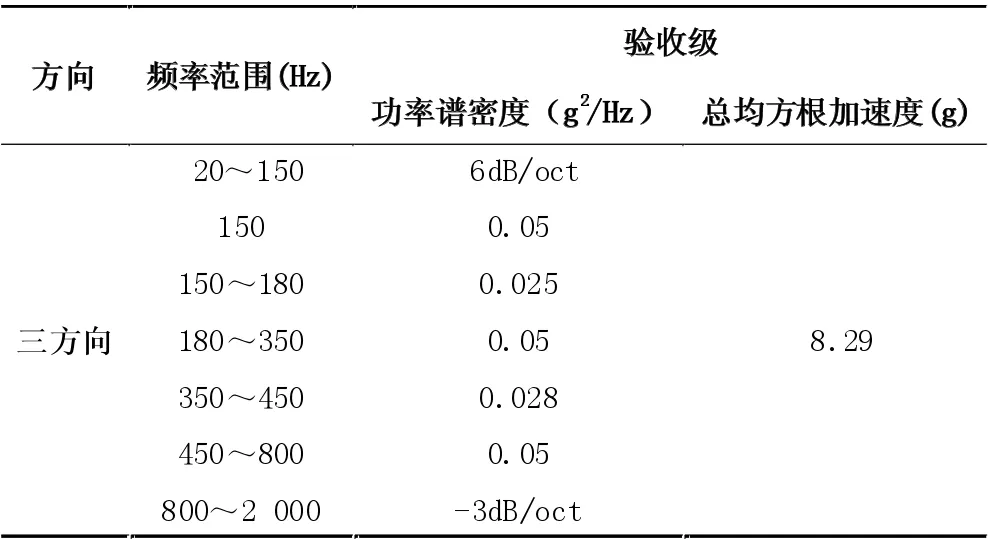
表1 卫星随机振动试验条件

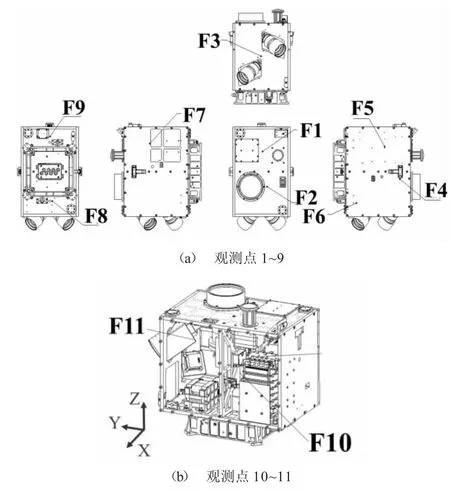
图2 仿真观测点位置

得到观测点位置加速度均方值见图3，并计算得到各观测点的均方根加速度见表2。

由图3 可以看出，卫星在随机振动试验条件激励下，观测点三个方向的加速度均方值均是呈上升、波动而后趋于平缓的走势。且不同观测点在同一方向上的曲线走势基本一致，只是不同观测点的振动幅值大小不同。振动幅值最大值位于150 Hz～800 Hz，这是由于卫星随机振动激励在150 Hz 达到了最大值，且150 Hz 与卫星主体结构的一阶振动频率138.21 Hz非常接近，因此卫星的振动在这个频率范围附近存在明显放大，且响应随激励的下凹而出现振荡。由表2可以得出，X 方向随机响应最大值为测点F2 的16.59 g，Y 方向随机响应最大值为测点F1 的14.65 g，Z 方向随机响应最大值为测点F3 的8.97 g，各测点的整体响应相对较小，证明卫星具有良好的抗振性能，能够确保卫星上安装设备的可靠运行。

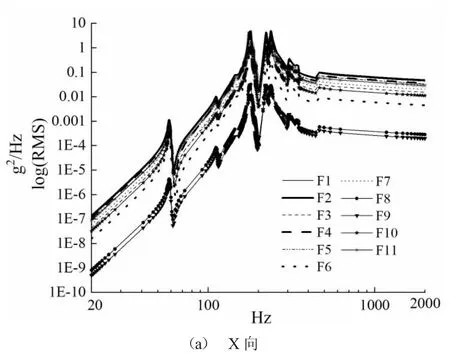
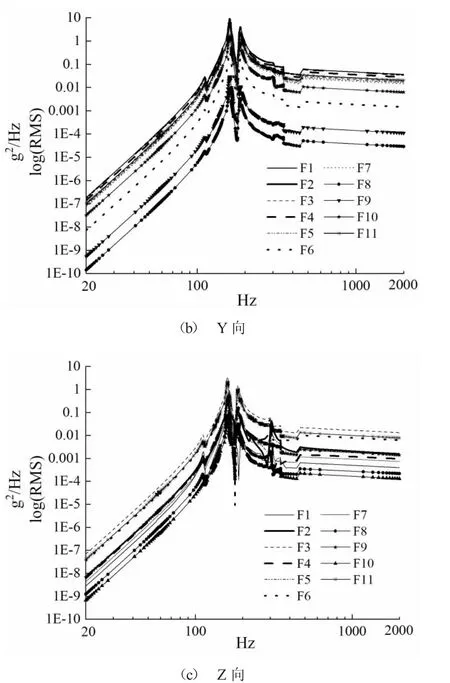
图3 观测点各向加速度均方值

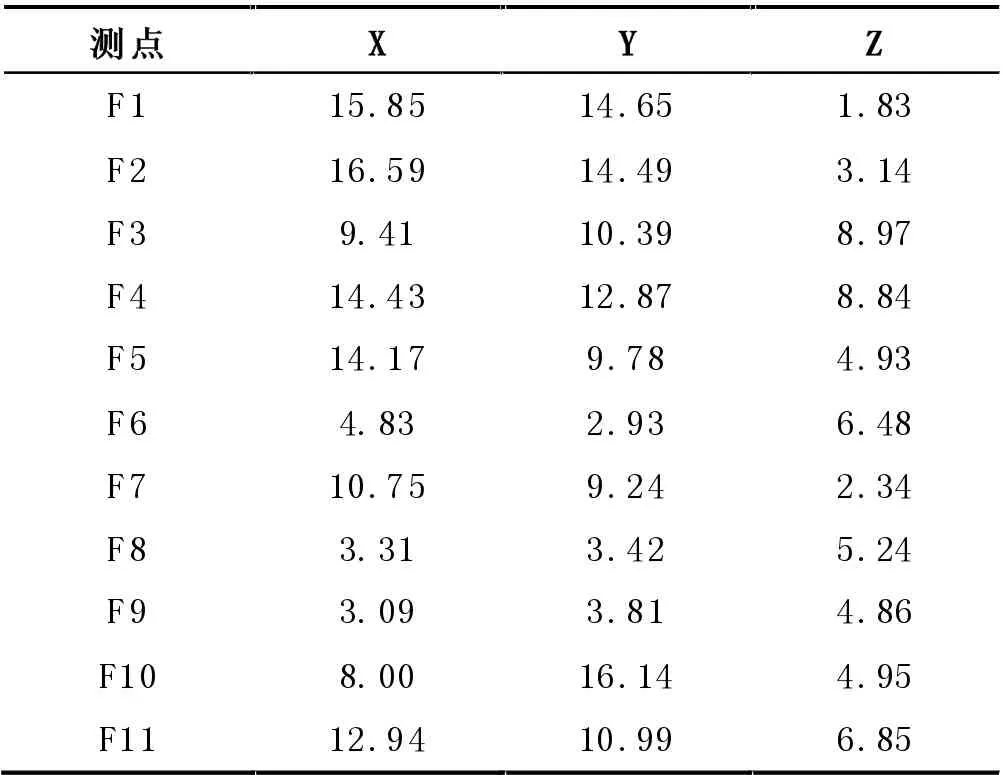
表2 仿真计算的各测点均方根加速度单位:g

3 随机振动试验

3.1 试验准备

在数值模拟的基础上，进一步开展卫星的随机振动试验研究。将卫星与振动试验台通过螺栓刚性连接，在与图2 对应的位置分别安装一组三向加速度传感器。

3.2 试验结果分析

随机振动试验在卫星的三个正交轴向分别进行激振，对试验各测点响应的均方根加速度进行统计并与仿真得到的测点均方根加速度对比，见表3。试验得到X 向随机响应最大在测点F7 为16.78 g，Y 向随机响应最大在测点F3 为16.6 g，Z 向随机响应最大在测点F4 为13.4 g，各方向振动试验后卫星综合电测正常，满足结构设计要求。

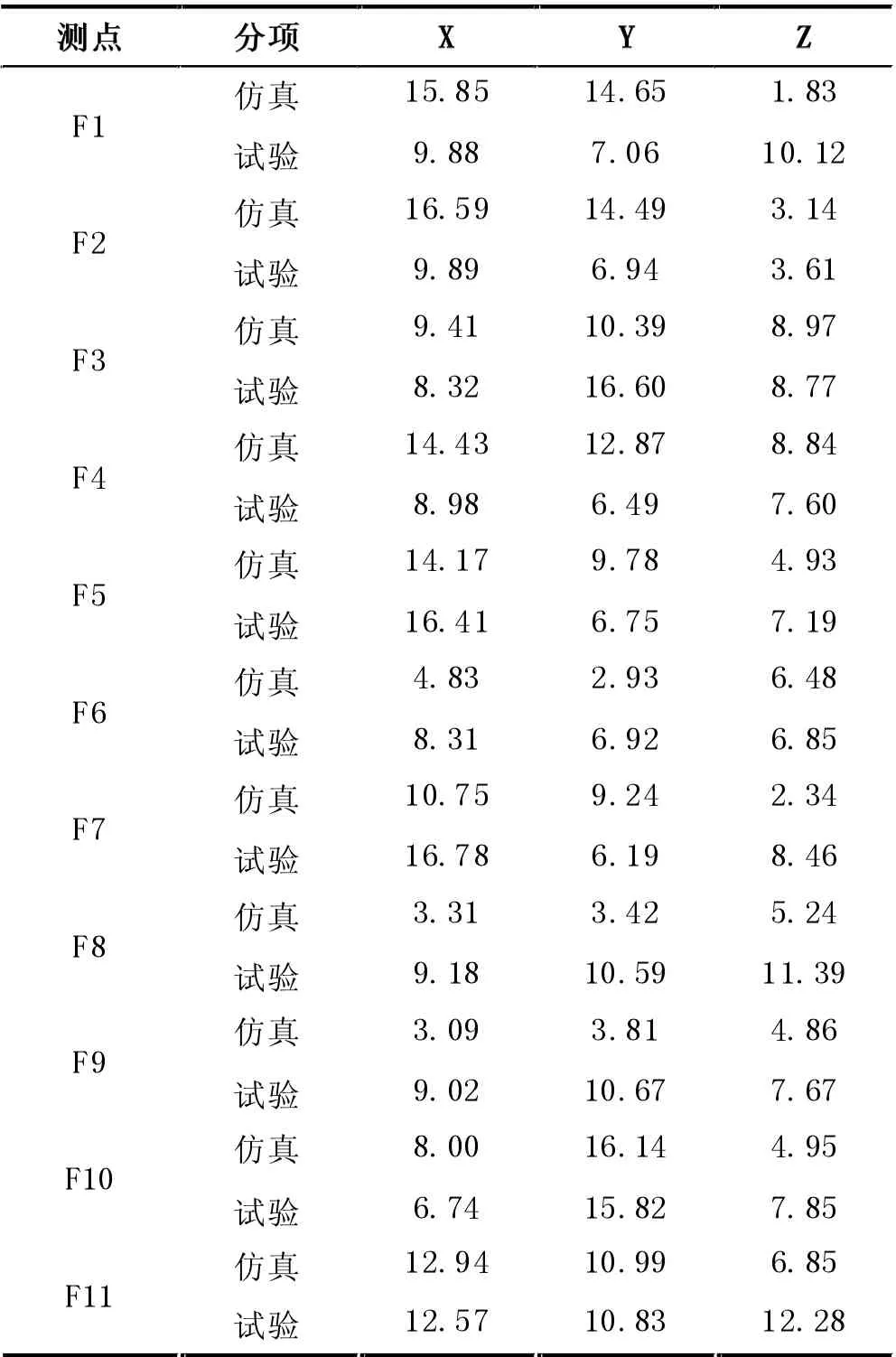
表3 随机振动试验和仿真中各测点的均方根加速度值

对比试验和仿真数据可以看到，仿真与试验得到的均方根加速度最大值不在同一测点，可能是仿真建模时模型简化导致的，建模过程中将卫星内部安装的各类电子设备简化为质量点耦合到相应的安装位置，虽能反应结构得质量特性，但质量点与电子设备的质心位置仍会存在一定差异，简化后对结构的振动信号传递存在一定的影响，使得仿真得出的最大均方根加速度测点位置与试验结果存在差异。仿真分析得到的部分测点数值与试验数值非常接近，如测点F10 的Y向、F11 的X 向和Y 向等，从整体来看，仿真得到具有最大值的测点与试验虽有一定差异，但仿真与试验得到的最大值能够很好的对应，因此仿真仍能反应部分结构的振动特性。

随机振动试验后，卫星整体结构无变形和破裂，各连接件无松动和脱落，被试卫星随机振动试验通过。