超参自适应支持向量回归及在滚齿工艺参数预测上的应用

曹卫东，欧阳骋，余 阳，李力泓，梁新利，姜博严

(1.河海大学 物联网工程学院，江苏 常州 213022;2.中国船舶工业综合技术经济研究院，北京 100081)

0 引言

支持向量回归(Support Vector Regression,SVR)在预测领域中取得了可喜成果[1-5]。在车削领域，王兴盛等[6]利用最小二乘支持向量机预测镜片精密车削表面粗糙度，并对工艺参数进行了分析。结果表明，刀具圆弧半径和每圈进给量对表面粗糙度影响较显著。ALAJMI等[7]使用SVR根据车削工艺参数确定刀具磨损，结果表明使用SVR估计工艺参数是可行的。在铣削领域，李尧等[8]使用模糊支持向量回归进行颤振诊断，预测准确率为97.3%。CHARALAMPOUS[9]使用SVR进行铣削切削力估算。在钻削领域，GU等[10]提出了基于SVR的磨损预测模型，预测结果与实验数据基本一致。然而，惩罚因子、内核类型等超参数都会影响到预测能力，上述研究大多采用人工经验设置超参数，需要耗费较长时间寻找合适的参数。因此，一些学者将亨利气体溶解度算法(Henry Gas Solubility Optimization,HGSO)[11-12]、樽海鞘算法(Salp Swarm Algorithm,SSA)[13-14]、蜻蜓算法[15-16]、蚁狮算法[17-18]、粒子群算法(Particle Swarm Optimization,PSO)[19,20]等智能算法应用于SVR的参数微调，提高预测精度。但是，由于搜索个体和迭代次数的增加，运行时间也成倍增加。尤其是在大数据预测方面，巨大的时间消耗困扰着许多学者。虽然使用K-means聚类分析进行数据预处理[21-23]可以大大缩短运行时间，但也会因为缺乏样本部分信息，降低预测精度。

可以发现，与智能算法结合后的SVR具有很好的预测能力，预测精度较高，但需要更多的运行时间，时间复杂度高；K-means聚类分析可以大大降低运行时间，但它需要割舍掉部分样本数据，损害了整体的预测性能。受到该问题的启发，本文主要对以下两个方面进行研究：①K-means聚类对数据集进行分析后，寻找一种智能算法优化SVR的超参数，能让预测精度、稳定性和时间复杂度综合最优，建立一种超参数自适应SVR方法;②使用不同维度的数据集以及滚齿工艺参数预测数据集对方法进行测试，显示其优异的综合性能。

针对上述问题，本文旨在寻找一种智能算法,以平衡预测能力与运行时间。哈里斯鹰算法(Harris Hawks Optimization, HHO)[24]是一种新颖的元启发式智能算法，具有非常优异的性能，但有落入局部最优解的缺陷。本文引入逻辑混沌映射，降低落入局部最优解的可能，以形成混沌哈里斯鹰算法(Chaos HHO, CHHO)，将该方法用于K-means聚类与SVR混合方法中，形成超参数自适应SVR方法，即Kmeans-CHHO-SVR。最后,在测试集上进行仿真实验，验证了算法的优越性。随后，将Kmeans-CHHO-SVR应用到滚齿工艺参数预测领域，验证其工程应用效果。

1 超参数自适应支持向量回归方法

Kmeans-CHHO-SVR的主要框架如下：①使用训练集和K-means聚类分析获取聚类中心CCs;②根据SVR超参数集群和CCs获得验证集的预测结果;③使用CHHO超参数集群，并记录最佳SVR超参数。重复步骤②和步骤③，直至达到终止条件。基于最佳SVR超参数，得到测试集的预测结果，预测过程如图1所示。SVR超参数集群X由SVR参数个体Xi组成。X={X1、X2、…、Xn}，其中n是个体数。

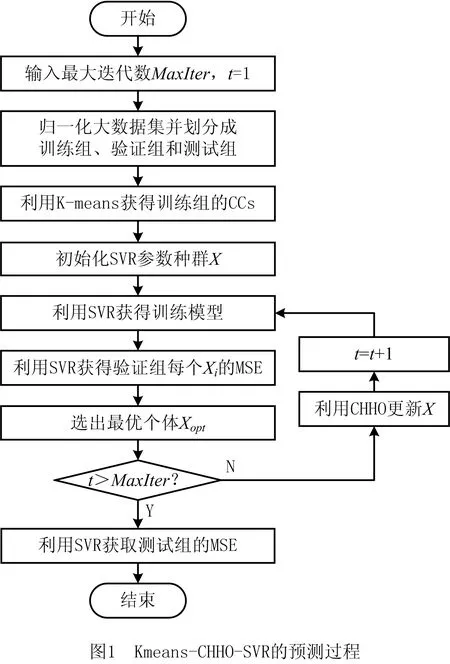
Kmeans-CHHO-SVR具体步骤如下：

步骤1设置最大迭代次数MaxIter，迭代次数t，t=1。

步骤2将数据归一化到-1～1之间，将其分为训练集集、验证集和测试集。

步骤3基于训练集，使用K-means聚类分析来获取聚类中心CCs。

步骤4输入SVR参数的下界LB和上界UB，根据LB和UB随机初始化X。

步骤5基于X和CCs，使用SVR获取训练模型。

步骤6根据训练模型和验证集获取验证集的均方误差MSEV。

步骤7找出第t代MSEV的最小值和最佳SVR参数Xopt。

步骤8若t>MaxIter，转步骤11；否则，转步骤9。

步骤9使用Xopt和CHHO的核心步骤来更新X。

步骤10t=t+1，转步骤5。

步骤11根据Xopt使用SVR获取测试集的均方误差MSET。

1.1 混沌哈里斯鹰优化器(CHHO)

哈里斯鹰算法(HHO)是HEIDARI等提出的新型启发式算法[24]，灵感来自哈里斯鹰的合作行为和追逐风格。哈里斯鹰的捕猎过程描述如下：

(1)探索阶段 使用式(1)模拟哈里斯鹰探索猎物的行为。

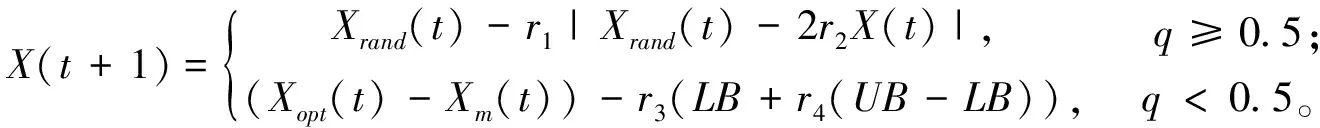
(1)

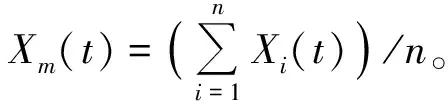
(2)开发阶段 该阶段哈里斯鹰根据兔子逃跑方式和环境影响在软围攻、硬围攻、渐进式快速俯冲的软围攻和渐进式快速俯冲的硬围攻4种追逐方式中选择一种去突袭兔子。

1)软围攻：

X(t+1)=△X(t)-E|J·Xopt(t)-X(t)|，

(2)

△X(t)=Xopt(t)-X(t)。

(3)

2)硬围攻：

X(t+1)=Xopt(t)-E|△X(t)|。

(4)

3)渐进式快速俯冲的软围攻：

Y=Xopt(t)-E|J·Xopt(t)-X(t)|。

(5)

哈里斯鹰根据莱维飞行进行俯冲：

Z=Y+S×LF(D)。

(6)

式中：D表示问题的维数，S表示1×D大小的随机向量，LF是莱维飞行函数，可以使用式(7)得到

(7)

其中μ和θ表示0～1之间的随机值。

鹰在软围攻阶段的位置更新可以总结为：

(8)

式中Y和Z可以使用式(5)和式(6)求得。

4)渐进式快速俯冲的硬围攻：

(9)

Y=Xopt(t)-E|J·Xopt(t)-Xm(t)|，

(10)

Z=Y+S×LF(D)。

(11)

CHHO核心操作的伪代码如图2所示，混沌值rC决定了算法进入了哪个阶段。rC是混沌随机值[25]，使用式(12)初始化rC：

科文学院新办公楼主要是行政人员,网络用户主要使用DB数据库访问、E-mail邮件和WWW访问,上网人数在60人左右;办公楼(老校区)主要是教学人员,网络用户主要使用FTP文件传输、E-mail邮件和WWW访问,上网人数在30人左右;新教学楼北区2～4层、教学楼部分楼层是学生机房,网络用户主要使用FTP文件传输、DB查询和WWW访问,上网学生数峰值在640人左右．网络拓扑结构模型如图2所示,其中,NIC为科文学院网络中心,Student为学生子网,Teach为教工子网,Office为办公子网.Student子网拓扑结构如图3所示.

rC(t+1)=4rC(t)(1-rC(t))。

(12)

1.2 K-means聚类分析

K-means聚类应用十分广泛，且十分有效[26]。K-means聚类算法的步骤如下。

步骤1设置初始聚类中心个数cNum并初始化聚类中心。

步骤2计算样本到每个聚类中心的距离,并将其分配给与其距离最小的聚类中心所对应的类中。

步骤3根据类中成员重新计算每类的聚类中心。

步骤4重复步骤2和步骤3，直到满足没有对象被重新分配给不同的聚类。

本文选择欧式距离作为距离度量，通过随机操作对聚类中心进行初始化。参数cNum的设置较为关键，实验1具体描述了它的选择过程和结果。

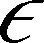
(1)RBF核函数：

KT(·)=exp(-γ|u-v|2)。

(2)Sigmod核函数：

KT(·)=tanh(γ(uTv)+coef)。

2 实例验证

验证基础条件包括:①计算机，CPU为Intel Xeon W-2123，内存为16 GB，WIN 10系统;②MATLAB R2018a;③LIBSVM;④大数据集，从UCI机器学习共享库[30]中获取。5个大数据集如表1所示。

表1 数据集的基本信息

为了探究Kmeans-CHHO-SVR的最佳设置和算法性能，实验由以下3个部分组成：首先进行了cNum设置实验，探究cNum的最佳取值;实验2比较了Kmeans-CHHO-SVR(CA0), Kmeans-SVR(CA1), Kmeans-HGSO-SVR(CA2), Kmeans-SSA-SVR(CA3), Kmeans-DA-SVR(CA4), Kmeans-ALO-SVR(CA5), Kmeans-PSO-SVR(CA6)和 Kmeans-HHO-SVR(CA7)在各个数据集下的预测精度和稳定性，分析了Kmeans-CHHO-SVR的性能；第3个实验研究了每个方法的时间复杂度。表2给出了各方法的初始参数设置。

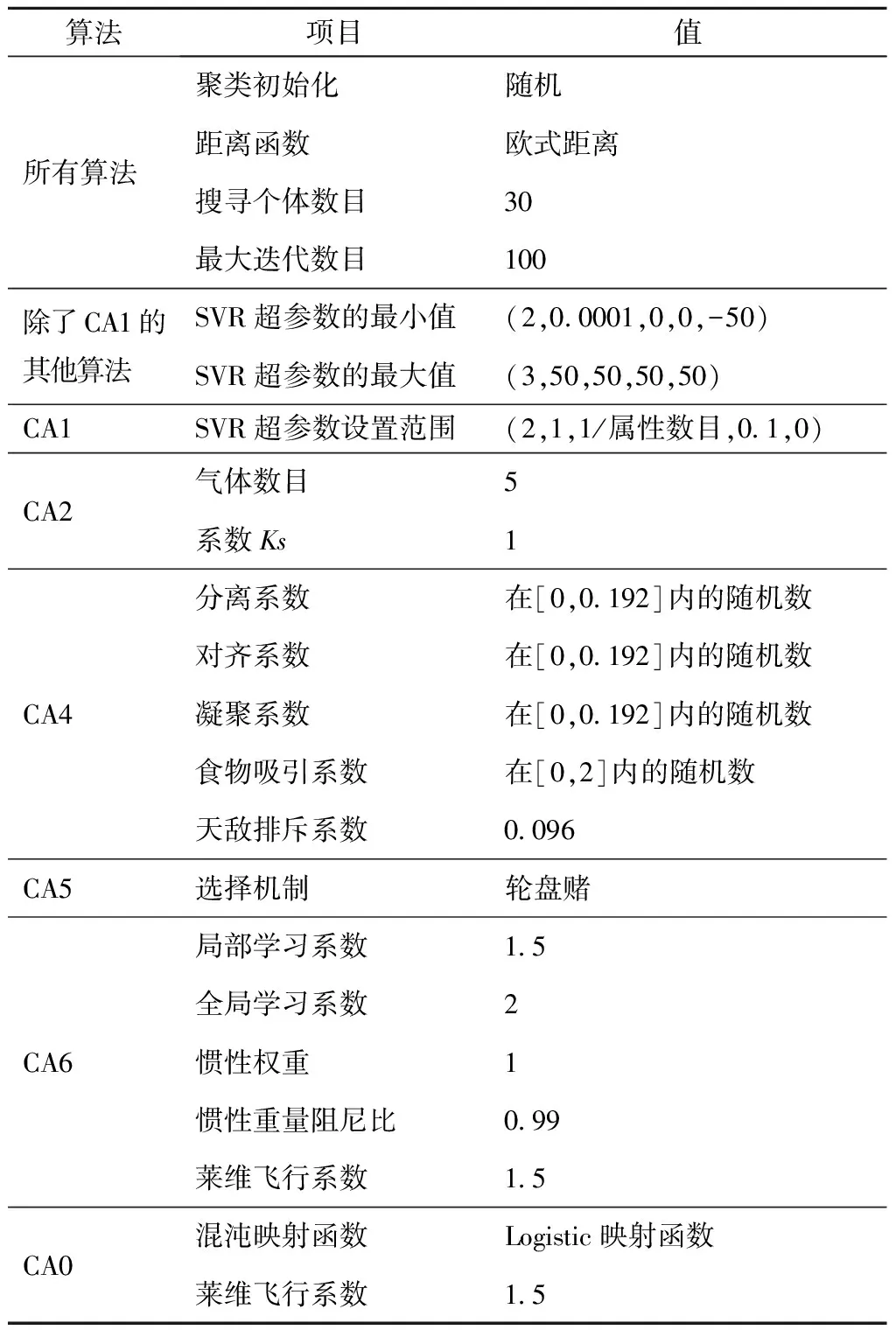
表2 参数设置

2.1 实验1：cNum设置

本实验研究了不同数据集下，Kmeans-CHHO-SVR的cNum设置对预测精度和运行时间的影响。图3给出了cNum取[20,200]下的MSET和运行时间结果，共计20次实验。可以看出，随着cNum的增加，MSET值在数据集D1～D4上相对稳定，在数据集D5上剧烈波动；运行时间在D1和D3上呈总体上升趋势，在另外3个数据集上出现了波动和上升，并最终有所下降。

为了选择合适的cNum，定义CMT=β·NMSET+δ·NTC，用来衡量cNum选取的优劣，CMT越小越好，其中β=0.8，δ=0.2，NMSET和NTC是归一化后的MSET值和运行时间。

表3给出了Kmeans-CHHO-SVR在5个数据集下的CMT值，OptC表示cNum的合适值。举例说明：在数据集D1下，cNum选择60最合适，对应的CMT为0.023。

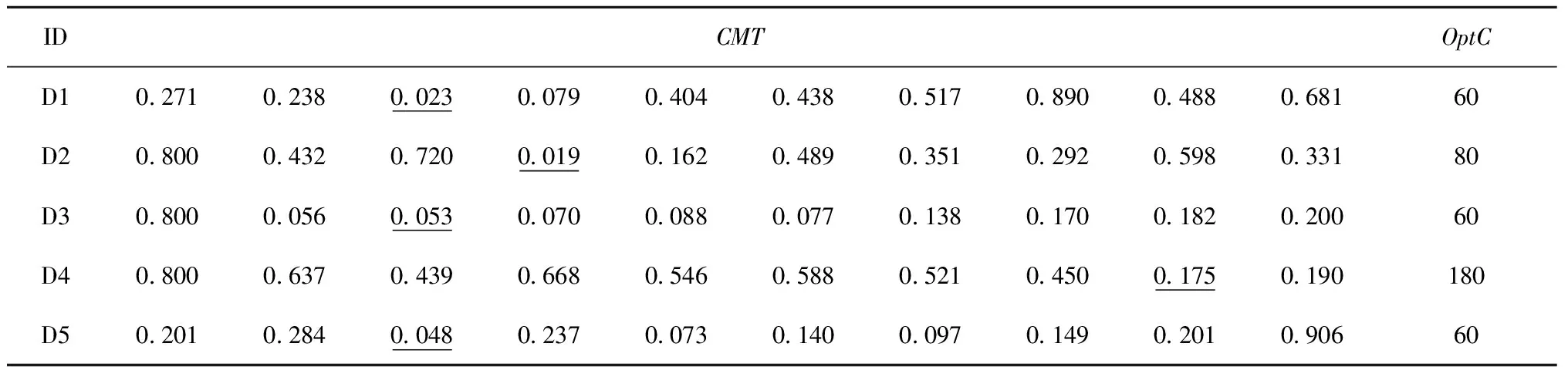
表3 CMT和OptC结果(CMT最小值用下划线标示)

2.2 实验2：预测精度和稳定性

为了检验Kmeans-CHHO-SVR的预测精度和稳定性，将其分别与CA1, CA2, CA3, CA4, CA5, CA6相比，验证其在数据集D1-D5上的性能。初始参数如表2和表3所示。实验选用十倍交叉验证，训练集、验证集、测试集的比例为98∶1∶1。根据第1章的方法步骤和数据集获取MSEV和MSET，重复该过程10次。

表4给出了预测精度(MSEV和MSET)的平均值(Avg)和标准差(Std)，图4和图5给出了MSEV和MSET的箱型图。结果显示，Kmeans-CHHO-SVR在数据集D1-D5上的MSEV和D2-D5上的MSET上表现最佳(联合最佳)。如图6所示，考虑验证集的标准差StdV，Kmeans-CHHO-SVR在D1、D3和D4上的输出最稳定；考虑测试集的标准差StdT，Kmeans-CHHO-SVR在D3和D4上的输出最稳定。

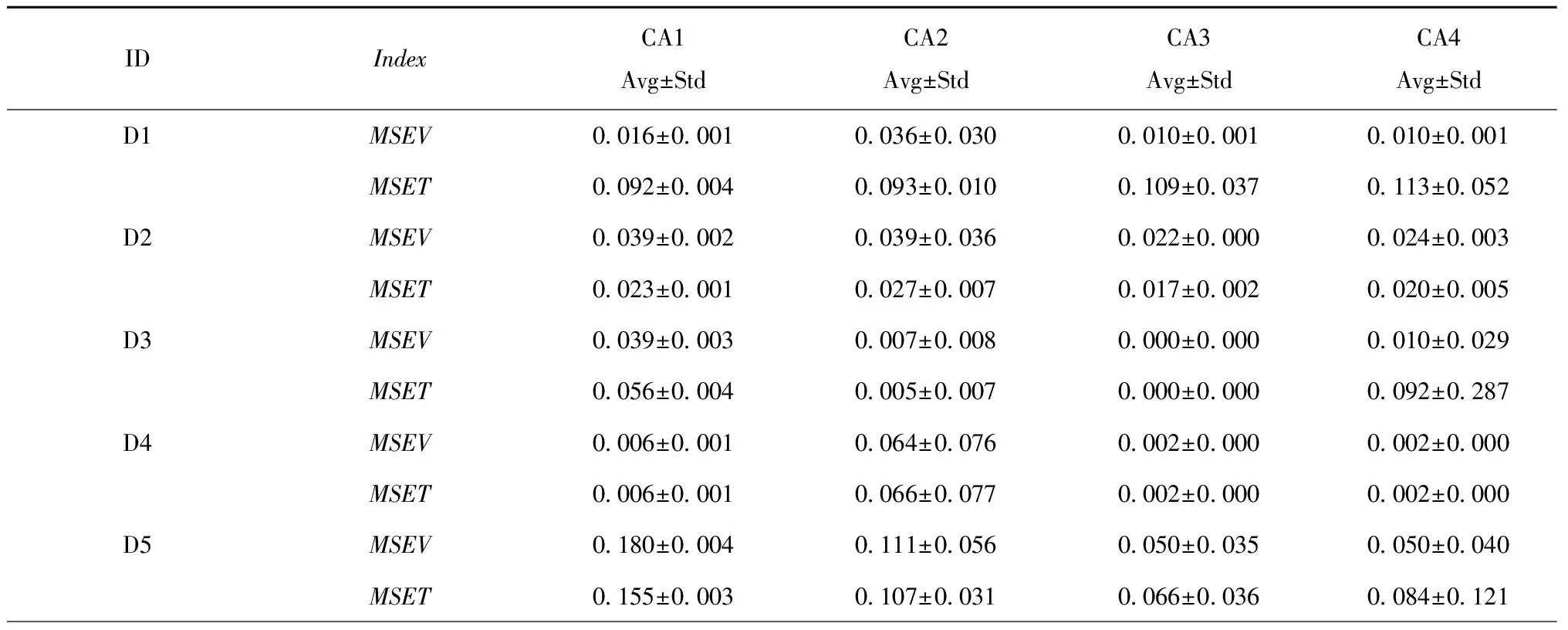
表4 MSEV和MSET结果

2.3 实验3：时间复杂度

时间复杂度描述了某个方法的运行时间。通常使用O进行表述。测算依据：本文方法属于组合方法，它的时间复杂度随着样本数目、样本属性数目、采用哪种核函数等参数而变化，采用O表述不能直观地与其他方法进行比较。故本文方法运行10次耗费的平均时间作为时间复杂度的测算依据。本实验通过比较相同的条件下，在数据集D1～D5上预测消耗的平均时间衡量复杂度，消耗时间越少，时间复杂度越低，测试过程与实验1几乎相同。定义CCRk评价时间复杂度如下：

(13)

(14)

式中:Crate表示归一化后的时间消耗，Cold表示时间消耗，CMin(CMax)表示最小(最大)时间消耗。nd=10。

表5给出了实验结果，可以看出，Kmeans-CHHO-SVR的表现不理想，但与其他算法的差距不大。

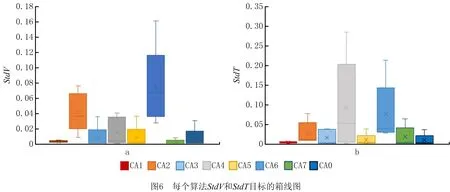
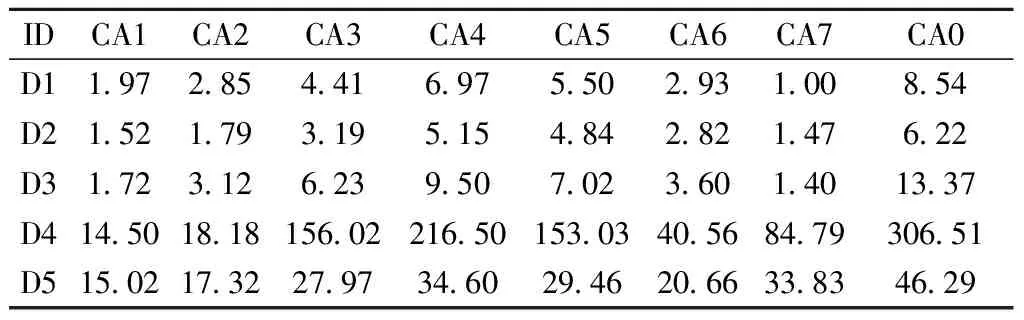
表5 各个算法的平均消耗时间

3 实验讨论

表6汇总了所有结果，其中“W”表示获胜，“T”并列，“L”表示失败。定义Rank评估算法综合表现，Rank越低越好。

(15)

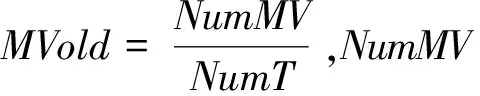
表6显示，Kmeans-CHHO-SVR模型的Rank值为0.226，综合表现最佳。可以看到，由于CHHO的存在，Kmeans-CHHO-SVR模型在许多数据集上预测精度最佳，且在D3和D4上拥有最好的稳定性，虽然混沌搜索增加了时间消耗，但模型取得了更佳的性能。因此，相比其他方法，Kmeans-CHHO-SVR效率更高，在处理大数据方面具有较大优势。

表6 各个方法的综合结果

4 工程验证

使用本文方法对滚齿工艺参数进行预测[31]，并在实际机床上进行加工。工程条件：①数控高速滚齿机YS3120CNC6-S，该机床为重庆某机床制造公司研发的六轴四联动智能高速滚齿机。配有西门子840Dsl数控系统，加工模数最大为6 mm; ②齿坯; ③计算机及MATLAB软件；④三丰高精度数显千分尺。实验基本步骤：将本文方法在MATLAB软件上实现，基于历史工艺参数决策数据生成滚齿参数，经工艺人员确认后进行编程并加工，使用三丰高精度数显千分尺测量跨棒距，以验证工件是否合格,加工设备如图7所示。

历史工艺参数决策数据如表7所示，种类为渐开线圆柱齿轮(包含非标齿轮)，材料为20CrMoTi，刀具为TiAlN涂层滚刀，加工精度为7级，采用逆滚轴向进给方式加工，一次走刀，走刀路径如图8所示。待决策问题Q={f1,f2,f3,f4,f5,f6,f7,f8,f9}={2, 0.349, 41, 0.456, 94.011, 13,71, 3, 4.005}，跨棒距要求为95.09±0.025 mm。使用本文方法决策出Q的工艺参数(382.6 r/min,1.84 mm/r)，决策耗时4.2 s。工艺人员依据该工艺参数编制数控程序，操作人员依据数控程序操作数控系统对工件进行加工，用三丰千分尺测量跨棒距为95.106 mm，工件滚齿合格，可以进入热处理及磨齿等后续工序。

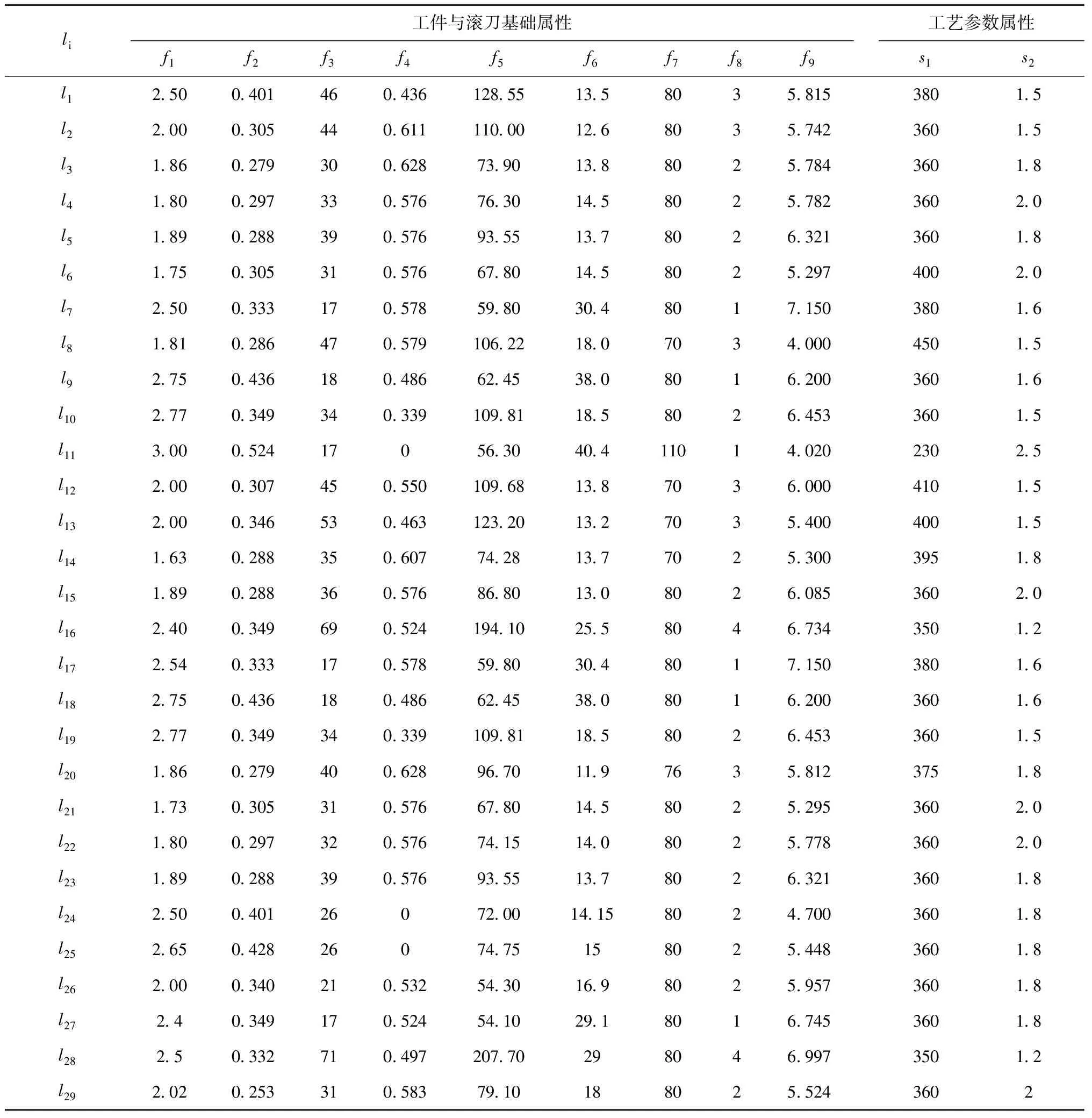
表7 历史工艺参数决策数据集

将本文方法(CA0)与CA1、CA2、CA3、CA4、CA5、CA6相比，由于没有Q的历史决策结果，无法比较预测精度，故本文在工件是否合格、决策耗时、切削耗时上进行比较。结果如表8所示，可以发现，本文方法在决策耗时上排名第3。在保证质量的情况下，切削耗时是最少的，排名第1。本文方法可以很好且快速地预测滚齿工艺参数，保证加工质量，且切削耗时少，与其他方法相比，具备一定优势,验证了本文方法的工程效果。

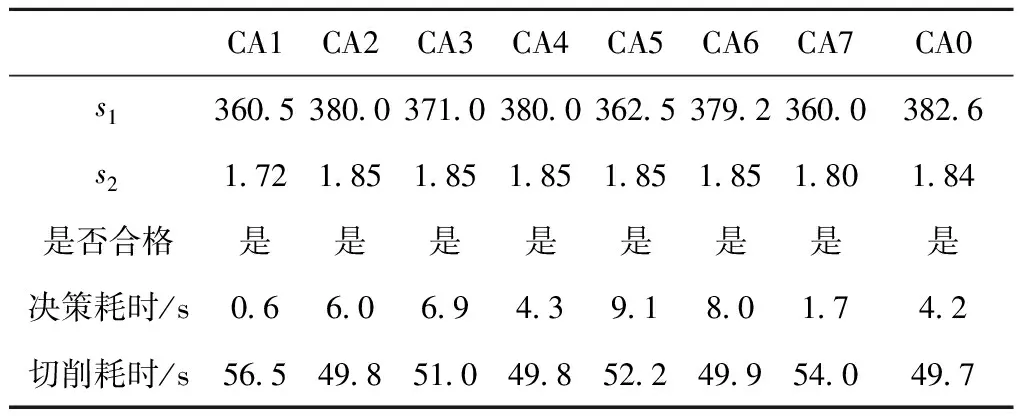
表8 各个算法应用效果比较

5 结束语

本文提出一种利用K-means聚类分析和CHHO优化SVR超参数的新方法，并进行了实验验证与工程验证。K-means聚类用于提高该算法的速度，CHHO用于提高预测精度。该方法能够实现预测问题中，特别是在大数据预测问题中的SVR超参数自适应调整，且能实现预测精度的提高，稳定性维持在较高水平。实验将Kmeans-CHHO-SVR与Kmeans-SVR、Kmeans-HGSO-SVR、Kmeans-SSA-SVR、Kmeans-DA-SVR、Kmeans-ALO-SVR、Kmeans-PSO-SVR、Kmeans-HHO-SVR比较，结果显示与其他成熟方法相比，Kmeans-CHHO-SVR的预测性能最佳，获得了最佳综合得分0.226。针对MSEV指标，本文方法在5组数据集上全面战胜其他方法，为最优；针对MSET指标，本文方法在4组数据集上战胜其他方法，为最优。针对StdVRK指标，本文方法排名第2；针对StdTRK指标，本文方法排名第3。综合评价显示本文方法综合性能最佳。此外，在滚齿工艺参数预测领域进行了工程验证，证实了本文方法的实际应用效果。综上，可以认为Kmeans-CHHO-SVR在预测领域拥有巨大潜力。未来将进一步提升本文方法的稳定性和降低方法运行时间，争取应用于更多更广的工业领域。