考虑性态变化的重力坝变形安全多级预警指标拟定

祖 安 君，黄 晓 丽

(1.南京水利科学研究院，江苏 南京 210029； 2.水利部大坝安全管理中心，江苏 南京 210029； 3.水利部建设管理与质量安全中心，北京 100038)

0 引 言

混凝土重力坝(以下简称“重力坝”)失事概率低，但与土石坝相比其溃决过程突然，后果更为严重。在重力坝事故的发展过程中，如果能及早准确地预测并预警，大坝的失事或可避免，即使不能完全避免，也能减轻失事后果。许多溃坝事故调查结果表明，重力坝失事大多都不是突发性的，而是一个由异常到险情，进而溃决的渐变演化过程，在损伤逐渐累积的不同阶段都会有相应的特征反映，这些征兆的出现使重力坝安全预警成为可能。重力坝失事的各个阶段，坝体混凝土结构会出现不同程度的异常变形或位移迹象，变形是最能够直观且综合反映重力坝坝体和坝基结构状态变化的效应量[1-3]。因此，提前准确捕捉到细微的重力坝变形异常变化特征，对于有效预警重力坝溃决突发事件发生、尽可能早地给下游公众提供可靠的预警信息、及时开展工程抢险和应急调度工作，从而降低大坝风险和减少灾害损失至关重要。而拟定客观、合理且符合工程实际的重力坝变形安全预警指标是大坝预警的关键环节，理论性强且复杂，一直是坝工领域的研究重难点。

重力坝变形安全预警指标是监测重力坝工作性态和评价重力坝安全状况的关键指标，对表征重力坝结构正常与否具有重要意义[4-5]。重力坝在投入使用后持续受到荷载作用，施工期技术人员在坝体、坝基等部位埋设了变形监测仪器，通过自动化监测或人工观测等方式，可获取重力坝运行过程中所积累的大量实测变形数据，由变形监测数据预测可能抵御荷载的能力，从而确定该荷载组合下变形的警戒值、危险值或极值[6-7]。通常采用置信区间法、典型小概率法和极限状态法等常规的方法，对重力坝变形安全预警指标进行拟定。对此众多学者开展了深入研究。如何军等[8]用卡尔曼滤波对某重力坝变形信息进行去噪，并采用置信区间法拟定了变形预警指标。李晓晨[9]、李磊等[10]选取混凝土坝坝体和坝顶某方向的径向位移极值作为变形空间，基于实测资料使用典型小概率法拟定了径向位移的预警指标。钱镜林等[11]基于小波变换和自回归模型特征多项式理论，拟定了混凝土坝变形安全预警指标。谷艳昌等[12]将结构计算与风险理论有机结合，拟定了考虑大坝风险的变形预警指标。张海龙等[13]在拟定大坝预警指标时，运用广义Pareto分布模型，用自动选取代替以往的超限期望图法确定阈值，提高了阈值选取的精度，拟定了位移预警指标。周稳忠等[14]一方面改良了计算方法，将正态分布修正为标准正态分布；另一方面分别拟定大坝变形水压、温度、时效3个分量的预警指标，然后进行叠加，作为最终的大坝变形安全预警指标，对典型小概率法作了改进。唐贤琪等[15]以极值理论为基础，针对安全预警指标拟定过程中现有阈值确定技术的主观性和不易操作等的不足，通过构建新的阈值序列，并结合统计学理论和人工智能手段，以预警指标的危险值与警戒值的差进行控制，将其逼近监测序列的标准差，拟定了更加合理、实用的预警指标。蔡忍等[16]综合考虑了大坝多测点变形监测序列，使用投影寻踪法对其降维，得到了反映多测点变形信息的加权序列，并采用云模型方法研究变形与环境量间的关系，拟定了某重力坝变形综合预警指标。

上述方法对重力坝性态评估均起到了一定作用，但这些方法在拟定预警指标前需进行统计检验，判断大坝变形样本的概率分布，而在指标实际拟定过程中，样本时常难以严格服从某一特定分布，因此通常假定大坝变形样本服从正态、对数正态等某一分布，该做法是存在主观影响的；同时，对于运行过程中存在安全隐患、具有失事风险的重力坝，仅依据工程经验将失效概率取为5%或1%，未对其运行性态所可能处于的不同阶段之间的临界点从客观角度进行确定或量化，缺乏理论依据，难以准确反映大坝运行性态，影响了拟定指标的精度。针对上述问题，本文运用最大熵原理构建重力坝变形样本随机分布情况下的分布函数，并基于典型小概率思想，结合层次分析法与粒子群算法，提出利用变形安全预警概率确定重力坝变形安全多级预警指标的方法，以期为重力坝变形安全预警指标有效拟定提供理论基础。

1 考虑变形样本随机性的分布函数确定

本文基于最大熵理论[17-19]，对分布形式不提前设定，而是直接依据重力坝变形统计信息所得的数字特征值做出估计，确定重力坝变形样本的概率密度函数和分布函数。

使用最大熵法确定重力坝变形样本的分布函数，首先需求解变形样本最大熵密度函数f(x)。由最大熵理论可知，若要变形样本的概率分布偏差最小，在依据已有样本约束下，变形样本概率密度函数的熵H(x)必取最大值，即：

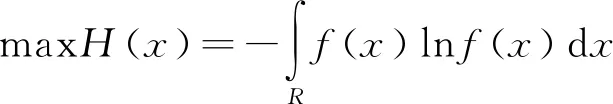
(1)

式中：R为积分空间；f(x)为随机分布下变形样本的概率密度函数。

约束条件：

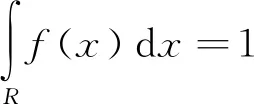
(2)

(3)

式中：μi为重力坝变形监测值随机变量X的第i阶原点矩，n为矩的阶数。为方便计算，式(2)～(3)合并为

(4)

通过调整式(1)中的f(x)使它的熵H(x)达到最大值，建立式(5)拉格朗日函数：

(5)

式中：λi为拉格朗日系数。

令∂L/∂f(x)=0，则有：

(6)

解得：

(7)

式(7)为变形样本最大熵概率密度函数的解析形式。通过将重力坝变形监测样本数据代入式(8)的n+1个非线性方程，可求解式(7)中的λi。

(8)

从λ0开始计算，将式(8)在λ0处用泰勒公式展开：

Gi(λ)≅Gi(λ0)+(λ-λ0)[gradGi(λ)](λ=λ0)=μi

(9)

则式(9)可简记为

Gτ=υ

(10)

求出τ后，新的迭代点为λ=λ0+τ，再求得新的τ值，逐步迭代直到收敛为止(τ小于某给定值，如0.000 1)。

通常采用数值积分的方法求解式(9)，其求解过程为：确定重力坝变形样本随机分布情况下样本概率密度函数f(x)的积分域，对该函数进行“截尾”处理，即认为f(x)在两端尾部(-∞，a]与[b，+∞)上的积分值为0，采用有限域[a，b]内的积分值近似(-∞，+∞)上的积分值。因此，只要积分域[a，b]取得足够大，就能将该种近似处理造成的误差降至精度要求之内，通常可取a=μ1-5σ，b=μ1+5σ，σ为式(3)大坝变形监测随机变量X的标准差。

2 考虑性态变化的重力坝变形安全多级预警指标拟定

在使用上述方法确定重力坝变形样本的分布函数后，需要确定重力坝在不同变形安全预警等级下的变形安全预警概率(失效概率)α值，进而求解相应的重力坝变形安全预警指标。本文将层次分析法和粒子群算法有机融合，对α进行求解。

2.1 重力坝变形安全预警概率确定方法

依据统计理论，大坝性态非正常即异常状态可视为小概率事件，概率区间划分为[0，α]，大坝性态正常为大概率事件，对应大概率区间(α，100%]，其中预警概率α范围为1%～5%，而α取值越小，对应拟定的预警指标值越大，为偏于安全保守考虑，预警概率取上限即α=5%较为合理，则重力坝正常运行和性态异常的概率区间分别为(5%，100%]和[0，5%]，若大坝存在坝体裂缝等安全隐患，则属于性态异常。为表征重力坝性态异常时安全隐患的不同严重程度，对[0，5%]小概率区间进行划分，将其划分为4个区间，并分别定义为失常、重度异常、轻度异常、基本正常，则这4种异常性态按照安全隐患程度由重到轻的3个临界点分别对应重力坝变形安全三级、二级、一级预警等级，它们落在[0，5%]的数值分别为重力坝变形安全三级、二级、一级预警概率。融合层次分析法和粒子群算法，提出了重力坝变形安全预警概率的确定方法，具体实施步骤如下：

(1) 构造重力坝变形安全预警等级评语成对比较判断矩阵。选取“三级、二级、一级”3级评语来反映重力坝变形安全预警等级，考虑到评语之间的差别性未知，使用以线性方式组成的定性术语来构造评语间的成对比较判断矩阵。以a为截断点，对1～9标度进行截断，a的左侧为L，右侧为M，记a为其中的截断点，则定性术语的映射为：L：[1，a)，M：[a，9]。评语等级差别性划分见表1。

表1 重力坝变形安全预警等级评语差别性划分

在对重力坝变形安全预警等级评语进行两两比较时，本文认为：三级安全预警等级比二级安全预警等级严格；三级安全预警等级比一级安全预警等级更严格；二级安全预警等级比一级安全预警等级严格。依据该规则，构造重力坝变形安全预警等级评语成对比较判断矩阵：

(11)

(2) 判断矩阵R的一致性检验与截断点确定。在变形安全预警概率确定过程中，需检验式(11)的一致性，以此确定表1中两个比例标度的截断点，即a的值。式(11)的一致性指标CI为

(12)

式中：n为R的阶数，λmax为R的最大特征根。

考虑到变形安全预警概率确定过程较为复杂，且人们的认知可能存在的片面性和问题的因素与规模有关，不能仅通过CI值检验一致性，故引入平均随机一致性指标RI(见表2)。

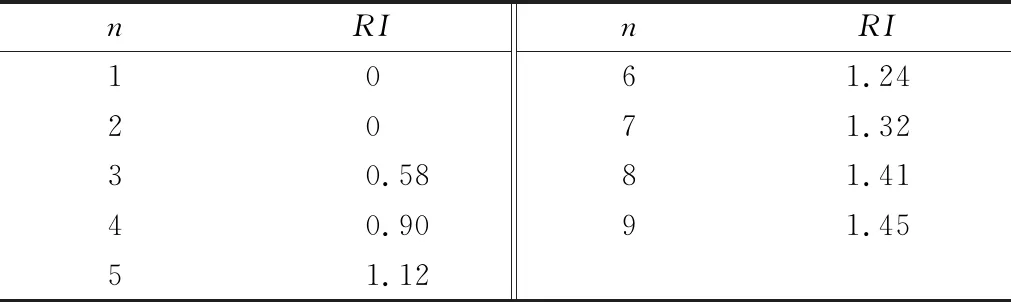
表2 RI取值

为综合反映CI与RI的作用，引入随机一致性比率CR判断一致性，即：

(13)

为使式(11)判断矩阵的一致性最理想，采用粒子群算法调整1～9标度中截断点的位置，并检验式(11)的一致性，从而求得最优截断点a的值。

令Xi=(xi)为第i组截断点粒子的位置，Vi=(vi)为粒子i的速度，Pi=(pi)为粒子i自身经历过的最好位置，Pg=(pg)为在当前粒子中搜索到最好的位置。寻优过程中，截断点粒子速度和位置的更新公式为

Vi(t+1)=ξvi(t)+c1r1[pi(t)-xi(t)]+c2r2[pg(t)-xi(t)]

(14)

xi(t+1)=xi(t)+vi(t+1)

(15)

式中：i=1，2，…，m；t为迭代次数；c1，c2为学习因子；r1、r2均为0～1随机数；ξ为惯性权重。

在每组截断点粒子位置下随机生成500个判断矩阵R，适应度函数选为500个判断矩阵的一致性比例CR的平均值，使用式(14)～(15)，利用适应度函数对所有截断点粒子评价其搜索性能，当适应度函数收敛并取得最小值时，对a寻优结束，用其最终结果作为变形安全预警等级评语集的1～9标度中最优截断点a。

(3) 变形安全预警概率求解。当求得重力坝变形安全预警等级划分的最优截断点后，即可获得在该截断点下CR最小时与之相应的矩阵R。设ω=(ω1，ω2，…，ωn)T表示与R最大特征根λmax对应的特征向量，即：

Rω=λmaxω

(16)

在求出特征向量ω后，将5%视为单位1，归一化特征向量。将重力坝变形安全预警等级的评语集在[0，5%]区间内划分，把归一化后特征向量各分量的数值作为重力坝各变形安全预警等级的概率分界值，于是求得重力坝变形安全预警等级的表达式为

(17)

式(17)中3个预警概率的具体求解过程可参见后文实例。

2.2 重力坝变形安全多级预警指标拟定

采用2.1节所述方法对重力坝各个变形安全预警概率进行求解，据此拟定表征重力坝不同运行性态的变形安全多级预警指标。

将充分反映重力坝运行性态变化的变形监测数据代入式(8)，并由式(7)求得变形样本最大熵概率密度函数f(x)，令δm为变形安全预警指标，当δ>δm时，重力坝将从隐患程度较轻的运行性态过渡到隐患程度较重的性态，与其相应的概率为

(18)

在变形样本随机分布的情况下，由式(17)确定不同的概率水平Pα。将式(17)中的变形安全预警概率值作为变形样本最大熵概率密度函数的概率分位点，即式(18)中的Pα，从而拟定重力坝变形安全一级、二级、三级预警指标。于是有：

当Pα=3.24%时，重力坝变形安全一级预警指标为

δ1m=F-1(δ，0.0324)

(19)

当Pα=1.27%时，重力坝变形安全二级预警指标为

δ2m=F-1(δ，0.0127)

(20)

当Pα=0.49%时，重力坝变形安全三级预警指标为

δ3m=F-1(δ，0.0049)

(21)

基于此，可实现对重力坝不同变形安全级别的多级预警，记δm为重力坝实测变形最大值。

(1) 当δ1m≤δm<δ2m时，为一级预警，应及时对现有重力坝变形监测资料进行分析，采取绘制过程线等方式准确把握和评估未来大坝变形发展趋势。

(2) 当δ2m≤δm<δ3m时，为二级预警，应加强巡视检查和重力坝变形安全监测频次，及时做好记录，在此基础上进一步分析该情况的产生原因，此外，及时采取恰当措施，密切关注大坝变形动态。

(3) 当δm=δ3m时，为三级预警，应即刻研判，并根据实际情况启动应急预案，对下游等公众发布有关报警通知，同时做好险情信息报送，有效防止险情发生，必要时应及时采取紧急情况人员转移、工程应急抢险等应急处置措施。

3 工程实例

3.1 工程概况

棉花滩水电站位于汀江干流，属Ⅰ等枢纽工程，总库容20.35亿m3，调节库容11.22亿m3，正常蓄水位173.00 m。设计洪水位174.76 m(0.2%)，校核洪水位177.80 m(0.02%)，重力坝级别为1级，最大坝高113 m，坝顶高程179.00 m。

大坝坝体从左往右共分为6个坝段，其中1号、2号、5号、6号坝段挡水，其余坝段为溢流坝段。选取5号坝段作为典型坝段，对该坝段坝顶沿上下游方向的水平变形进行分析，规定向下游方向为正，向上游方向为负，分析时段为2013年1月1日至2018年12月31日，采用本文提出的方法拟定该坝段坝顶向下游方向水平变形安全一级、二级和三级预警指标。

3.2 多级预警指标拟定

5号坝段在桩号0+218断面布置了2个正垂线测点PP10、PP9和1个倒垂线测点PP8，分别监测179.00(坝顶)，140.00，120.00 m高程处的水平变形，采用垂线坐标仪进行自动化监测，监测精度0.1 mm，测点上下游方向水平变形实测过程线见图1。变形样本为每年变形最大值δmi(见表3)。

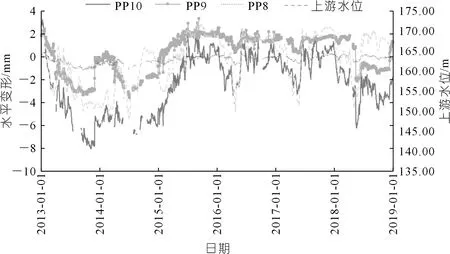
图1 5号坝段测点上下游方向水平变形过程线

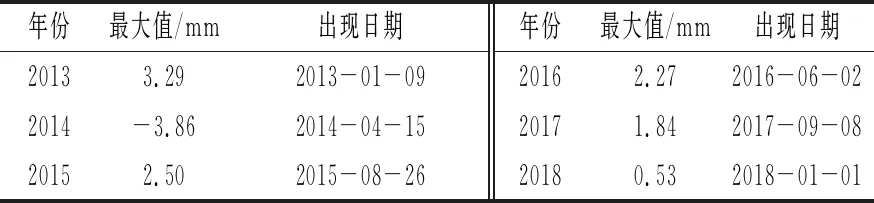
表3 5号坝段坝顶下游方向水平变形极大值统计

由图1可知：2014年测点PP10测值普遍较低，无异常值，主要因该年库水位相对其他年份较低，最高和最低库水位分别为165.89 m和148.10 m，明显低于其余年份，而水位变化对坝顶变形影响相对显著。综上，表3所列水平变形极大值均可靠，可用于拟定预警指标。典型小概率法拟定的失效概率5%和1%下该坝5号坝段坝顶向下游水平变形安全预警指标分别为5.359 mm和7.125 mm。

3.2.1重力坝变形安全预警概率求解

采用前文方法，计算表3变形样本的前一阶、二阶、三阶、四阶原点矩与相应标准差，并以此确定数值积分区间，具体结果见表4。

表4 各阶原点矩及标准差

接下来求解重力坝变形安全预警概率。采用2.1节方法，通过判别式(11)的一致性，基于粒子群算法，在每组粒子位置下，随机生成500个判断矩阵R，根据式(13)，分别求解每个判断矩阵的CR值，用生成的所有判断矩阵CR值的平均值作为适应度函数指标，适应度函数迭代过程见图2。

图2 适应度函数迭代过程

经计算，当截断点为4.34时，式(11)的一致性比例为最小，相应的一致性指标分布见图3。于是，以最优截断点4.34为限制条件，并以一致性比例最小为控制条件(即目标函数)，求解判断矩阵特征向量，具体结果见图4，其中V1、D1分别为式(11)判断矩阵的特征向量和特征值，即式(16)中对应于判断矩阵最大特征值3.063 5(D1的第一行第一列)的特征向量ω为V1的第一个列向量(0.938 0，0.367 6，0.141 9)，将ω归一化得向量ω1(0.648 0，0.254 0，0.098 0)，再将ω1以5%为单位1进行归一化得ω2(0.032 4，0.012 7，0.004 9)，则归一化后，特征向量ω三个分量的数值分别对应变形安全一级、二级、三级预警等级的概率值，即式(17)表示的重力坝变形安全预警等级的概率为[0.49%，1.27%，3.24%]。

图3 一致性指标分布

图4 判断矩阵特征值和特征向量计算结果

3.2.2重力坝变形安全多级预警指标拟定

根据上述分析，将求得的3个变形安全预警概率值分别作为式(18)中重力坝变形样本最大熵概率密度函数相应的α分位点，即：重力坝变形安全一级、变形安全二级、变形安全三级预警概率α1、α2、α3依次取值3.24%，1.27%，0.49%，据此拟定三级重力坝变形安全预警指标：

δ1m=F-1(δ，0.0324)=5.88 mm

δ2m=F-1(δ，0.0127)=6.89 mm

δ3m=F-1(δ，0.0049)=7.79 mm

将本文方法拟定结果与文献[20]拟定结果进行对比发现：设计洪水位下变形安全预警指标为6.01 mm，校核洪水位下变形安全预警指标为7.90 mm，两者吻合。本文拟定的变形安全一级安全预警指标略小于结构分析法拟定结果；变形安全二级预警指标略大于结构分析法拟定结果，两者量级一致；变形安全三级预警指标与结构分析法拟定结果较为接近。通常结构分析法拟定坝顶测点向下游变形安全预警指标时，以强度和稳定为控制指标，并选择最高库水位与极值温降作为荷载工况，但实际坝顶向下游变形达到极大值时水位非最高、温降也非最大，故结构分析法拟定指标偏大，应大于变形安全一级预警指标，但考虑到变形安全二级预警指标对应重力坝性态轻度异常与重度异常的分界，大坝较多区域已屈服，故变形二级预警指标应与结构分析法设计工况下拟定指标量级一致且数值接近；变形安全三级预警指标对应重力坝性态重度异常与失常的分界，为变形极值，而结构分析法中用校核洪水位下的偶然荷载工况并以强度、稳定为控制拟定的预警指标也为变形极值，故两者数值应接近。

4 结 语

针对变形安全预警概率取值易受人为主观因素影响的问题，依据统计学小概率理论将预警概率和重力坝存在隐患时的性态相联系，引入层次分析思想，以线性定性术语建立重力坝变形安全预警等级评语成对比较判断矩阵，适应度函数为随机生成的所有判断矩阵的一致性比例均值，并有机结合粒子群算法对术语比例标度的截断点进行寻优，进而确定变形安全多级预警概率。工程实例应用结果验证了该方法的有效性和实用性，拟定的预警指标更为客观。