河床冲淤对越江盾构隧道管片内力及变形的影响
2022-12-05李方利,李雪
李 方 利,李 雪
(1.中铁建昆仑地铁投资建设管理有限公司,四川 成都 610041; 2.西南石油大学 地球科学与技术学院,四川 成都 610500)
0 引 言
隧道设计需要考虑到水压力和土压力,对于常规隧道来说,水位及覆土厚度基本上不发生变化,一般作用在隧道上的荷载基本是常量[1-4]。然而,对位于江底的隧道而言,一方面作用在隧道上的泥沙荷载随着河床的冲刷淤积而不断变化,进而影响隧道管片受力和变形;另一方面随着枯水期和洪水期的交替出现,水位变化也会影响作用在衬砌上的荷载,改变盾构隧道受力状态。尤其对于河床存在深切槽的部位,河床冲刷淤积量范围较大,厚度也较大,在此部位的江底河床冲淤及水位变化一方面影响管片内力,另一方面也会引起管片接头张开,如果张开量超出一定限值会引起接缝漏水,影响列车的正常运行,严重时将造成很大的事故[5-7]。因此,河床深切槽部位隧道的设计是越江隧道设计的关键之一,有必要对越江隧道工程中河床冲淤及水位变化对管片内力及变形的影响进行研究[8-11]。
由于深切槽淤积冲刷对越江盾构隧道中的管片内力及变形影响的复杂性,已有众多国内外学者对其进行了分析研究。如Schotte等[12]根据越江盾构隧道的现场试验数据,分析了潮汐水位变化对盾构隧道管片内力及变形的影响;戴志仁[13]、沈林冲[14]等通过对河床冲刷淤积荷载变化的理论计算研究,提出并确定了越江盾构隧道最小安全覆土厚度;周顺华等[15]根据越江盾构隧道管片的现场测试结果,提出了适用于计算大直径越江高水压盾构隧道内力的改进算法。
本文通过分析长江南京段深切槽河段水位、水文地质及河床冲淤演变规律,得到越江盾构隧道处最大最小淤积量及洪水位、枯水位。采用梁-弹簧计算模型,考虑不同淤积冲刷及不同水位工况组合,计算冲刷淤积对大直径盾构隧道管片内力的影响及管片张开量大小。研究成果可为后续越江隧道设计施工提供参考。
1 工程概况
南京地铁3号线下穿的长江段位于浦珠路站至滨江路站区间,区间全长约3.3 km,过江段约2.1 km。其中,河床深切槽位置靠近北岸(摆幅前后100 m),隧顶埋深约18 m。在300 a一遇冲刷条件下,隧道顶部埋深仅有5 m。深槽段穿越地层主要为粉细砂和含砾中粗砂层,土层渗透系数较大,透水性好,地层的物理力学指标如表1所列。此外过江段最大纵坡为28‰,最大变坡点为30‰,最大变坡点位置刚好位于河床深泓摆幅范围内。图1为南京地铁3号线过江段浦珠路站至滨江路站区间纵剖面。
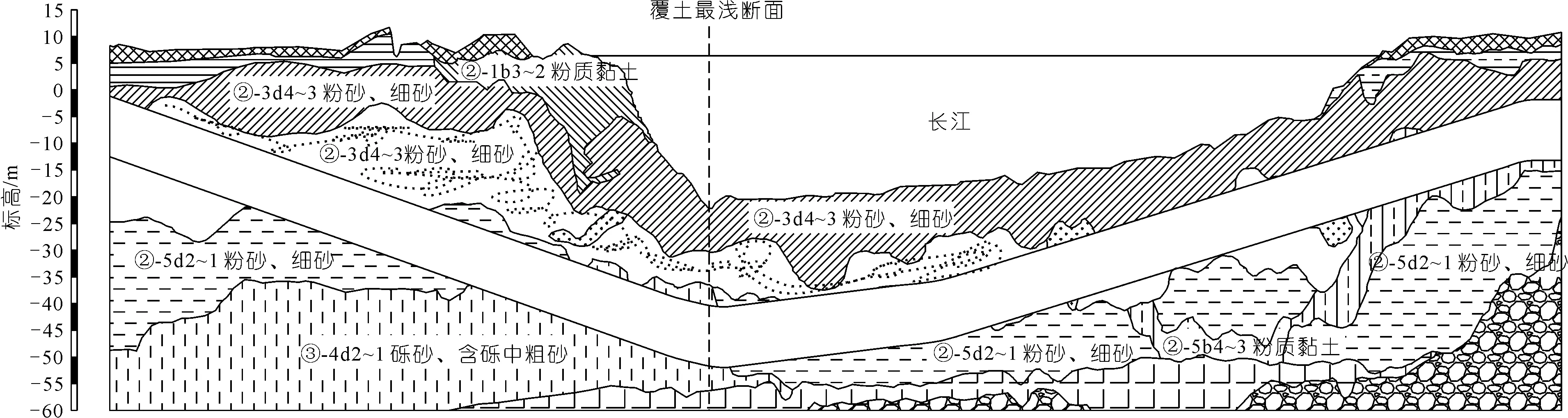
图1 南京地铁三号线浦-滨区间纵剖面

表1 隧道上覆土层特性及土压力参数
2 深切槽部位水文地质
该段地貌上横跨长江漫滩平原区、长江河谷区、长江一级阶地地区,地形低平,地势向长江河谷缓倾。地铁穿越长江处江面宽约2 km,水下地形呈不对称缓“U”形,靠近北岸边坡变化较陡,南岸边坡变化平缓。该段主要位于长江漫滩平原区,为受长江汛期影响的易涝区。区段土层结构复杂,含水砂层发育,地下水丰富,江水与地下水水力联系密切。在长江两侧存在较厚的淤泥质粉质黏土,粉砂、细砂及粉土存在液化可能。
2.1 水文泥沙特征
长江南京河段多年平均年径流量约为8 940亿m3。年内水量分配过程为:1月份最小(枯),到4月份水量开始增长,4~5月增长率最大,7~8月份出现最大值,然后逐渐减小,10月份以后水量明显减小,至次年1月,水量又出现最枯。对于年内输沙量分配过程,多年月平均输沙量(率)、含沙量等以7月份为最高,1月份为最低,且从4月份开始递增,至7月份达最大值,然后逐月递减。年内输沙量主要集中在汛期,汛期输沙量占全年输沙量的87.7%。长江南京段水位的涨落主要决定于长江径流的变化,也兼受潮汐、下游支流入汇和风力等影响。南京河段属感潮河段半日潮型,潮差枯季大,汛期小,随径流的增大而减小,其河段水文泥沙特征值汇总如表2所列。

表2 水文特征值汇总
2.2 工程地质条件
南京地铁三号线区间盾构穿越地层基本以粉细砂为主,最深处水深28~30 m,具有较大的水压。粉细砂层在上部水压作用下,尤其是浅部②-3d4~3层为可液化土,呈松散-稍密,盾构隧道施工时容易出现渗水。渗水后会导致土层松动,最终导致塌方,应及时进行支护,防止渗水。当采用中密-密实粉砂、细砂层作为隧道穿越土层时,地基稳定性较好;盾构隧道穿越长江两侧软弱土层时,应进行地基处理。
2.3 河床冲淤演变分析
长江南京河段上承新济洲河段,下接镇扬河段,上起下三山、下至三江口,主泓长约65 km。沿河段自上而下有七坝、下关、西坝和三江口等4个束窄段,河宽均在1 km左右。相邻两窄段间水域开阔,出现分汊河段。第一、二束窄段之间为梅子洲汊道,为双分汊河型;第二、三束窄段之间为八卦洲汊道,为弓型分汊;第三、四束窄段原为兴隆洲汊道,1985年堵左汊以后西坝以下为单一的龙潭弯道。大胜关-西坝河段全长40 km,包括梅子洲和八卦洲两个分汊河段。图2是南京河段河势图。
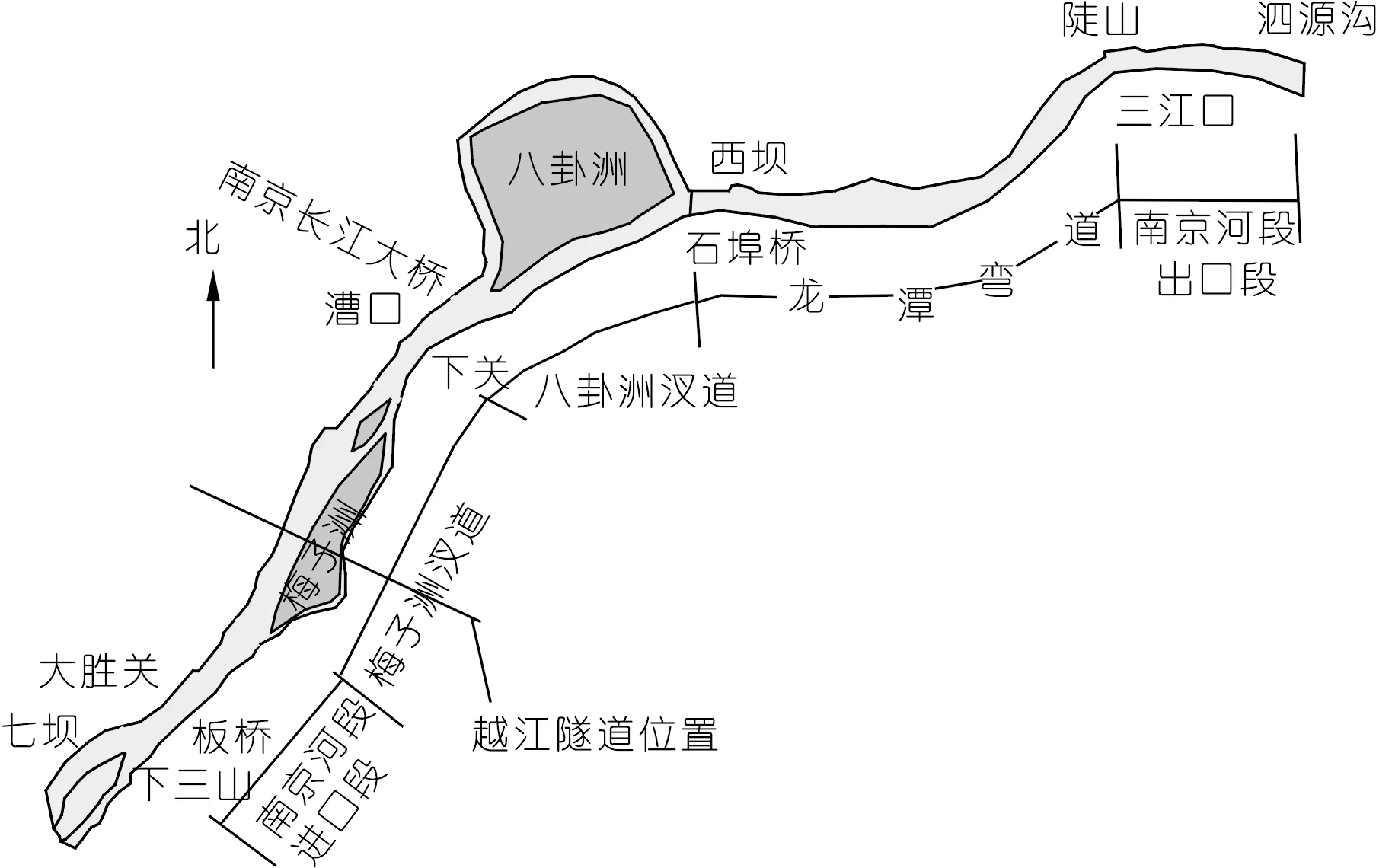
图2 南京河段河势
根据动床模型试验结果:在300 a一遇试验条件下隧址断面最低冲刷高程为-26.741 m;在考虑上游建库情况下,300 a一遇洪水条件下隧道过江断面最低冲刷高程为-29.461 m。
3 考虑冲淤及水位变化的盾构隧道结构计算
选择南京地铁3号线越江隧道江中覆土最浅断面作为典型断面,其计算断面具体位置见图1。为了进一步研究深切槽淤积冲刷对越江盾构隧道管片内力及变形的影响,采用梁-弹簧法计算隧道衬砌内力[16]。
3.1 梁-弹簧模型法
梁-弹簧模型法可以真实地反映盾构隧道管片的分块数、分块位置、管片接头转动弹簧刚度的大小,环间接头的配置及其剪切刚度的大小,由错缝拼装方式不同引起的拼接效果的差异[17]等,其隧顶垂直荷载的确定同均质圆环法,计算模型见图3,但梁-弹簧模型通过地层弹簧来评价地层抗力,计算模型见图4。

图3 传统方法计算模型

图4 梁-弹簧结构计算模型
采用空间结构进行计算,并用圆环径向抗剪刚度Kr和切向抗剪刚度Kt来体现管片环间的传力效果。结构与地层间的相互作用按管片全周布置仅受压线弹簧来模拟,受拉弹簧自动取消。用梁-弹簧模型可以对任意一种管片的组装方式以及接头的位置进行模拟,同时计算管片环接头上产生的剪力。
3.2 计算工况及荷载
在深切槽段,根据隧道结构抗浮计算,为满足300 a一遇洪水期的抗浮要求,隧道结构顶部与300 a一遇冲刷线之间的覆土需不小于5 m且要考虑300 a一遇冲刷线左右100 m的摆幅,且该段覆土最小厚度约12.07 m,本文同时考虑300 a一遇江底河床冲刷线和100 a一遇洪水位及枯水期对隧道结构稳定性影响,共选取6种工况,如表3所列。土压力计算时,竖向土压力按计算截面以上全部土柱重量计算,水平压力按朗肯静止土压力理论计算,根据上覆土体类型采用水土分算。
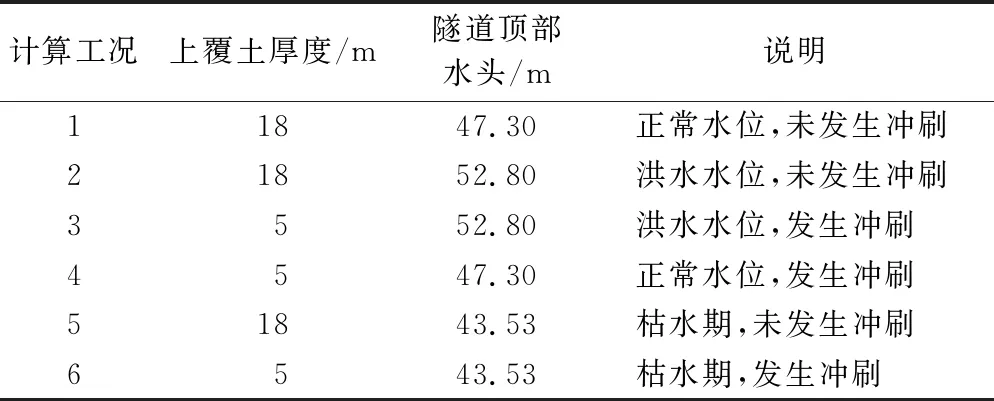
表3 过江隧道计算工况
3.3 管片拼装方式及相关参数的确定
梁-弹簧模型中选取3环管片进行计算。管片采用错缝拼装,环与环之间的错开角度为24°,每环管片布置形式如图5所示。管片内径10.2 m、外径11.2 m、宽2 m,采用通用衬砌环,衬砌圆环分为8块,5标准块(SB)+2邻接块(SL)+1封顶块(SF)。

图5 管片拼装方式
由国内外部分盾构隧道在管片接头旋转刚度系数方面的取值经验可知,随着隧道直径的增大,管片接头旋转刚度值也相应增大,其中直径大于10 m的盾构隧道,其管片接头旋转刚度系数的取值范围一般为0.8×105~8×105(kN·m)/rad。
梁-弹簧模型计算中,相邻环之间的影响通过与环间相对位移对应的剪力来考虑,将相对位移分为管片环半径方向和切线方向2个分量。以Qsr代表半径方向的剪切力,δsr为环间接头半径方向的相对位移,则半径方向的剪切弹簧系数可以定义为
ksr=Qsr/δsr
(1)
以Qst为管片切线方向的剪切力,δst为管片切线方向的相对位移,则管片切线方向的剪切弹簧系数可以定义为
kst=Qst/δst
(2)
剪切弹簧系数ksr与kst大多通过试验或者类似工程经验取得。一般剪切弹簧系数取值在100 000~500 000 kN/m,也可以把剪切弹簧系数设为无限大或者非常大以偏大地考虑错缝拼装效果,但是环间弹簧剪切弹簧系数取很大值时,剪力的计算结果会变大。
管片与地基土之间采用曲面弹簧进行模拟,土体弹簧为仅受压单元,土弹簧轴向刚度计算公式为
K=mbs
(3)
式中:m为围岩弹性抗力系数,MPa/m;b为衬砌纵向计算宽度,m;s为相邻土弹簧长度间的距离,m。
3.4 计算结果分析
梁-弹簧计算模型如图6所示。图7表示3号线在高水位下,冲刷前后管片弯矩的变化情况,其中左半圆为未冲刷的弯矩图,右半圆为冲刷后的弯矩图。根据本次研究目的,此处主要对第二环(封顶块位于隧道顶部)管片最大弯矩截面以及管片纵缝位置的内力进行分析。

图6 梁-弹簧计算模型弯矩示意

图7 高水位条件下冲刷前后管片弯矩(单位:kN·m)
表4为管片衬砌本身的弯矩及轴力情况,从中可得到如下结论:

表4 各工况下管片弯矩、轴力
(1) 最大弯矩工况是工况2,即洪水水位、未发生冲刷工况,其中正弯矩为417.87 kN·m,负弯矩为-390.28 kN·m,两者弯矩量值均不大。
(2) 通过工况1、工况2、工况5的弯矩值比较可知(工况1为正常水位、工况2为洪水水位、工况5为枯水水位),水位的变化对盾构管片弯矩的影响较小。
(3) 图8列出了各水位情况下,盾构隧道管片所受的最大正负弯矩在冲刷前后的变化情况。表5列出了冲刷对盾构管片弯矩的影响程度。冲刷使得最大正负弯矩的降幅平均达到56%,因此冲刷对隧道管片内力有很大程度的降低作用。

图8 各水位情况下冲刷前后管片最大正负弯矩变化

表5 冲刷对管片弯矩的影响
表6为管片接头弯矩及张开量结果,各个接头的位置如图9所示。由于该环管片的封顶块位于隧道顶部,模型左右对称,因此只需选择半边管片的接头进行分析即可,其中正号表示接头发生外张,负号表示接头发生内张。接头1,3和接头4发生外张,而接头2发生内张。
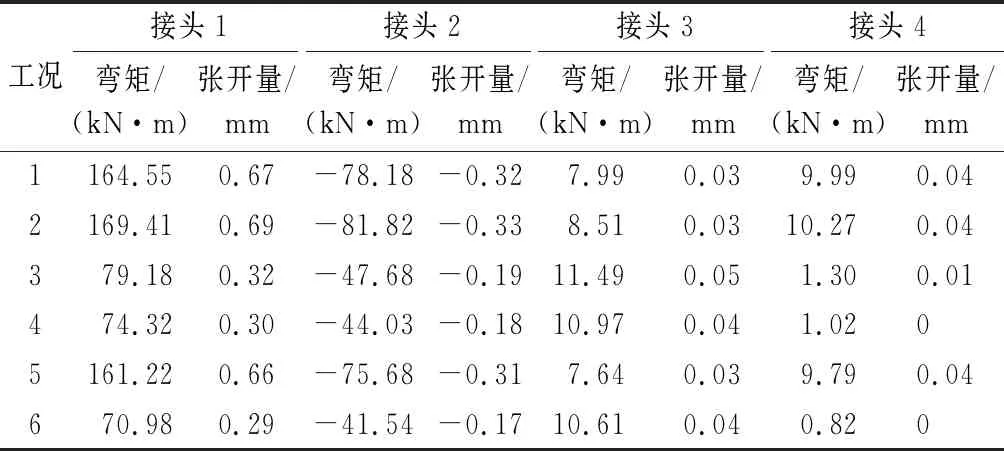
表6 各工况下管片间接头弯矩及张开量
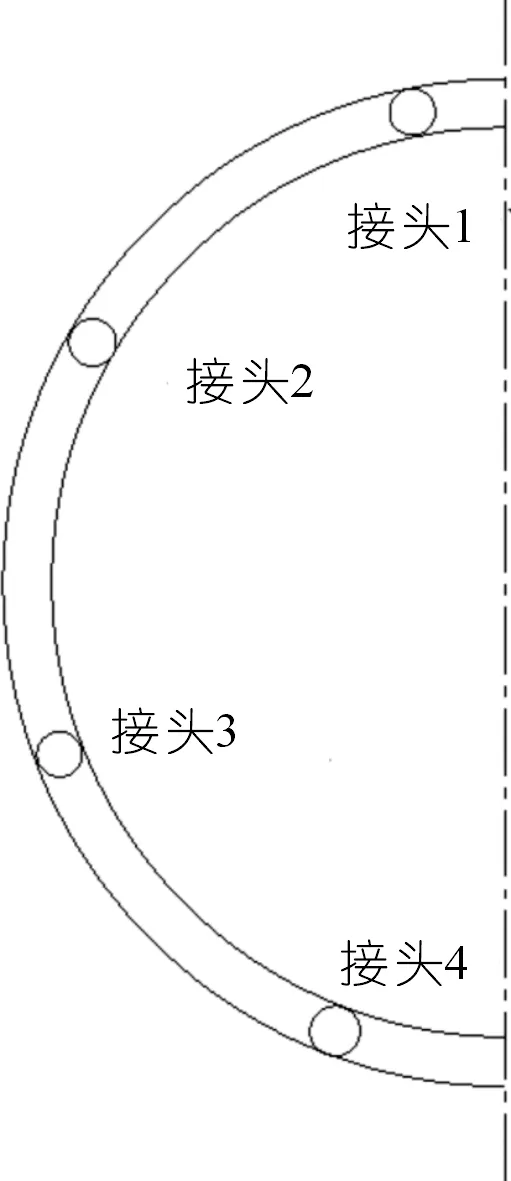
图9 各接头位置
(1) 接头最大弯矩及最大张开量均出现在工况2,即洪水水位、未冲刷工况,其中最大外张量为0.69 mm(接头1),最大内张量为-0.33 mm(接头2)。
(2) 从工况1,2,5各接头弯矩及张开量变化情况可知,水位的变化对接头内力及变形影响较小。
(3) 图10分别列出了各水位情况下,管片接头(考虑到接头3和接头4数值太小,在图中未列出)张开量在冲刷前后的变化情况。由表7可知,冲刷使接头1的张开量减少了56.4%,接头2的张开量减少了45.5%。综上可知,河床冲刷对接头所受弯矩及张开量有很大程度的降低作用,但并不改变接头的张开方式(即接头1,3,4冲刷前后都为外张,接头2冲刷前后都为内张)。
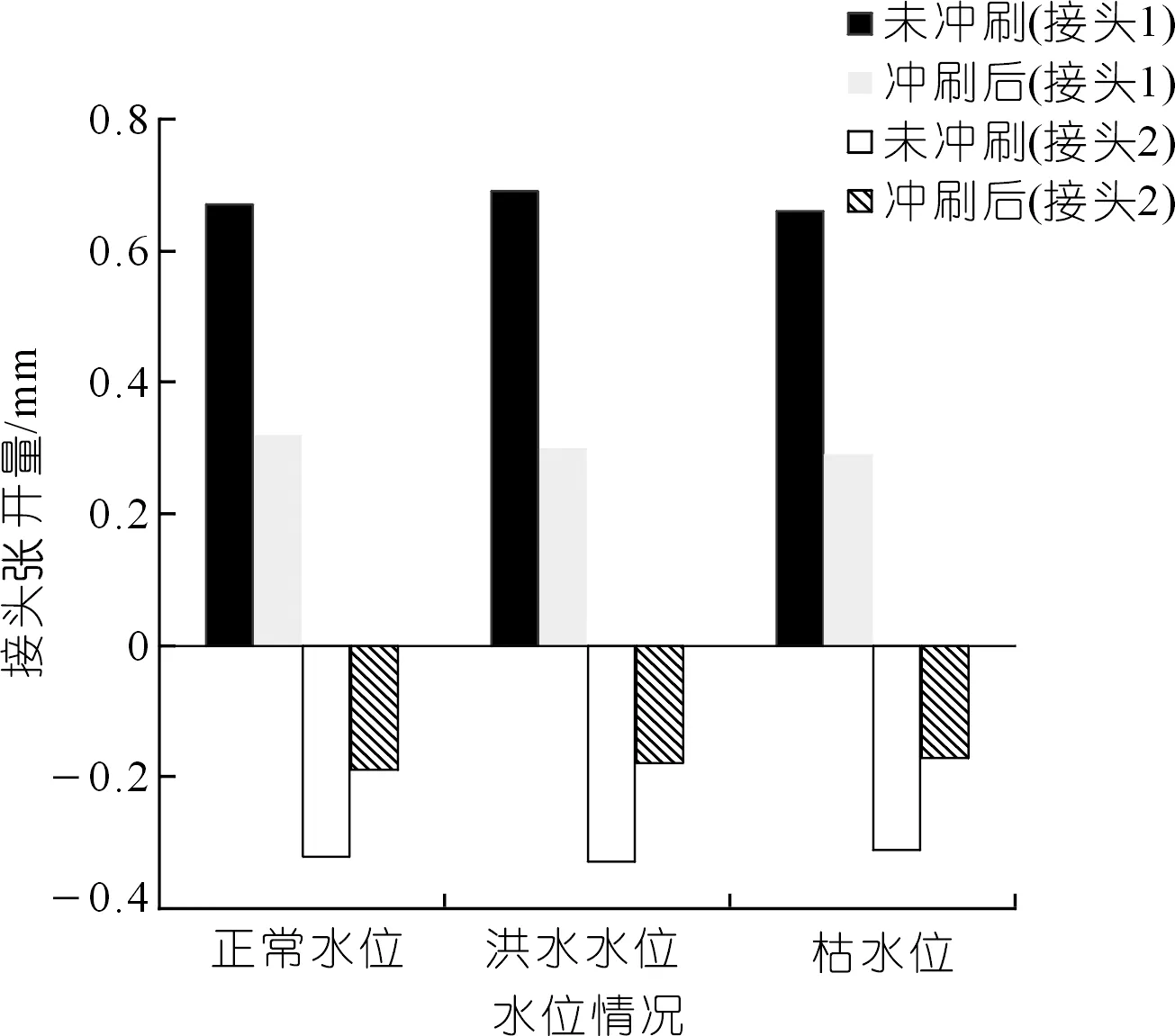
图10 各水位情况下冲刷前后接头张开量变化

表7 冲刷对管片接头弯矩及张开量的影响
深切槽段冲刷和淤积对管片结构的受力、弯矩及结合部位张开度的影响主要受盾构隧道顶部覆土厚度变化的影响。本文主要考虑的是深切槽段盾构隧道在300 a一遇冲刷线和100 a一遇洪水位及枯水期等典型水位对隧道结构的稳定性,未发生冲刷的地层视为淤积工况进行分析研究,但本文暂未分析淤积量对于盾构管片的影响,下一步将开展淤积工况的研究。
4 结 论
(1) 采用梁-弹簧计算模型,考虑300 a一遇冲刷线和100 a一遇洪水及枯水期水位,计算冲刷前后及典型水位组合工况下管片内力及接头变形量。管片接头最大弯矩及最大张开量均发生在洪水水位、未冲刷工况。
(2) 水位的变化对管片弯矩的影响不大,而河床冲刷使得最大正负弯矩的降幅平均达到56%,冲刷使隧道管片内力有很大程度的降低。
(3) 水位的变化对接头内力及变形影响很小,冲刷使接头1的张开量减少了56.4%,接头2的张开量减少了45.5%,河床冲刷使接头所受弯矩及张开量有很大程度的降低,但并不改变接头的张开方式。
