空间岩层属性的预估计算方法

赵小平，王 伟，代佳和，李 捷

（1．西安石油大学 经济管理学院，陕西 西安 710065；2．西安石油大学 理学院，陕西 西安 710065）

引 言

空间岩层属性的准确预估对于研究地质岩层结构，开展空间地质探索，以及合理安全地开采石油等资源具有十分重大的意义。近年来，人们在利用单一地震参数进行空间岩层属性的研究和预测岩性的分布情况方面取得了一定成果，但用这种方法不能客观预测复杂、细微的岩石属性变化，因而很难准确描述岩性特征。目前，三维建模是解决空间岩层属性预估的有效途径之一，三维空间的属性建模可以用于求解空间内部物理、化学等属性参数［1-3］，然而，现阶段的三维建模研究主要针对空间中实体进行几何形态建模，而对实体内部属性的建模研究仍存在一些不足。

三维空间的属性建模中求解属性值的较普遍的方法是对三维空间中的特定属性进行插值处理。在三维空间中选取部分数据点进行测量得到一定数量且离散的数据，这些数据可以部分或者全部反映出空间特征，利用这些已知数据进行插值，可以预测未知数据的属性特征。常见空间插值的方法有：反距离加权插值算法、样条函数插值法和克里金插值法等［4-17］。这些方法普遍受观察点和数据体规模影响较大，而导致计算插值速度较慢，插值效率降低，效果不理想。不仅如此，当采样点分布不均匀时得到的插值结果误差较大，且存在误差迭代积累等诸多因素影响属性值的准确性。

本文主要是通过对已有的空间岩层属性的预估方法进行研究对比，对现有的研究预测的数学计算方法加以改进，提出一种基于多步迭代属性插值算法，适用于处理三维空间岩层属性插值预估问题和利用计算机构建三维空间岩层属性模型。

1 常见预估计算方法

1．1 反距离加权插值算法

地理事物或属性在空间分布上互为相关，存在聚集、随机、规则分布的特征，即两个物体间距离越近越相似。基于此，陈鹏等［1］提出一种反距离加权插值算法。

反距离加权法是利用距离对空间离散数据点进行确定属性的一种插值方法。距离预测位置较近的测量值与较远的测量值相比，对预测值的影响更大。该方法为距离预测位置较近的点赋的权重较大，权重随距离的增加而下降。

反距离加权法基于彼此距离较近的事物要比彼此距离较远的事物更相似，待估测点的属性值为各个已知点属性值的加权平均值的思想，构造公式为

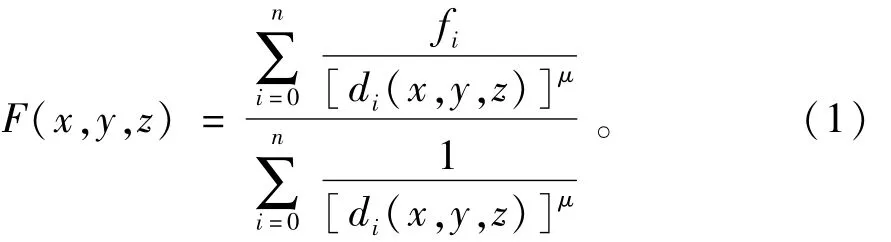
式中：fi为已知数据点的函数值；（x，y，z）为插值点 坐 标； （） 为 离 散 点 坐 标；di（x，y，z） ＝离散点的距离。μ为任意正实数，通常取值为2，定义的幂值越高，相邻数据受影响越大，插值数据就越接近最近采样点的值。

利用待估点的属性值为各个已知点属性值的加权平均值的基本思想，反距离加权插值算法是一种常用的空间插值方法。

1．2 基于B样条的插值算法

基于B样条的插值算法是一种大规模插值方法，在数据量较大时，B样条插值算法插值效率较高且插值效果不易受外界因素的影响，插值效果比较理想，其插值效率快且插值效果能很好地逼近散乱数据点。该方法无法保证插值曲面能够完全通过所有插值点，生成的是在一定误差范围内的拟合曲面，具有一定的适用性。

设在三维空间中，有一离散点集合P ＝｛（x，y，z，p）｝，坐标系 XOYOZ中有一数据体 Ω，（）是其中的离散点。可以构造m×n×k个双三次B样条曲面片集合来逼近表示离散点集P，m表示沿X方向将Ω分成m等分，同理沿Y方向将Ω分成n等分、沿Z方向将Ω分成k等分。由控制点网格体Φ来定义这个m×n×k个双三次B样条曲面片，Φ均匀地覆盖在数据体Ω中，为（m＋3）×（n＋3）×（k＋3）的控制点网格体。

由这些控制点定义的B样条函数为

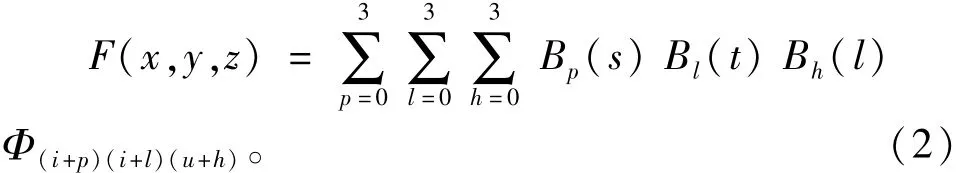
B样条函数插值算法则通过求解覆盖一定数据体的控制点网格体，可对大规模且分布不均匀的三维数据点进行插值［3］。

1．3 滑动邻域克里金插值算法

克里金算法是一种流行的空间插值方法，是国际上公认的空间插值方法，也是地质统计学的主要方法。该方法根据已知样本的空间位置和相关程度，求出未知区域线性无偏、估计误差最小的数值估计。克里金算法源于简单易行的普通克里金，传统的克里金法选择所有的已知点进行插值，计算时间较长，尤其大规模采集数据的情况下，甚至无能为力；并且在实际中，真实的协方差是估计出来的，而数据测量时又不可避免产生误差，这就有可能导致在大的邻域上插值产生的均方差比在相对较小的邻域上插值时的均方差要大。故在计算前对每个待插点分别选择其邻域内的一部分已知点作为原始估值计算数据。因此，如何选取邻域点成了克里金法亟需解决的问题。基于此，在普通克里金的基础上产生了一种高效的滑动邻域克里金方法［7］。以变程步长进行矩形网格邻域划分，再通过以下步骤实现：

（1）原始点集合中加入采样点数据。

（2）根据所有已知点进行全局范围求变程α。

（3）依托上述求得的变程α，采用邻域划分方法进行正方形网格单元划分。

（4）将已知原始点分配到其各自所属的网格单元。确定各点所在的邻域位置。

（5）对所有待插点进行遍历确定其所在邻域，运用全局变程α建立局部范围内的克里金方程组，通过求解方程组得到待插点结果。

基于变程的滑动邻域克里金插值方法是一种全局求变程，并根据已知变程进行局部克里金方程组计算的插值方法，可以在三维空间的曲面高程数据插值中得到应用。

1．4 基于距离场的属性插值算法

地理学第一定律指出“任何事物与其他事物之间都是相关的，距离越近相关性越强”。距离是地学研究中一个非常重要的空间属性，常用于构建三维地学变量，并在此基础上进行各类三维空间分析与地学模拟。根据表达侧重点的不同，三维地质模型分为实体模型和场模型两类。实体模型旨在显式构建三维空间的地质体结构（如断层、不整合面、矿体等），又称为几何模型。场模型是利用规则的或者不规则的体元对三维地学空间进行划分，用连续变化的体元属性值来表示三维空间中的物理和化学属性（如孔隙度、品位、电阻率等），又称为属性模型。

根据一系列属性等值线剖面／断面数据进行三维空间插值问题，黄岸烁等［15］提出一种基于距离场的三维空间属性插值方法。首先，根据对应属性等值线轮廓生成三维等值面；然后，构建属性等值面的三维距离场；最后，对于空间内任意点属性，根据其两侧等值面的距离场数据进行线性插值求取，从而生成整个三维空间内的属性场模型。该方法可用于揭示地下空间物性分布和预测隐伏矿体等。

2 一种空间岩层属性预估插值的新算法

2．1 方法

（1）选择插值区域

选择待预估节点的平面区域作为插值区域。区域中应包含（n＋1）2个同类型离散插值采样点及其相关属性。

（2）生成插值结点

对于区域中的离散插值采样点 Bi，j＝（xij，yij），i，j＝0，1，2，…，n。其中 xij，yij分别为已知点横、纵坐标，tij为点某一已知岩层属性值。构造相应的插值采样结点 Pi，j＝（xij，yij，tij），i，j＝0，1，2，…，n。

（3）多步迭代属性插值

对于区域中任一点（x0，y0）的岩层属性值，按如下步骤计算：

对于r＝1，2，…，n及i，j＝0，1，…，n-r，令P0，0i，j其中u，v为变量，u，v∈ ［0，1］。

（4）计算预估点属性值

由Pn，n0，0＝（f（u，v），g（u，v），t（u，v）），令f（u，v）＝x0，g（u，v）＝y0，解方程求出u0，v0。代入t（u0，v0）＝t0，t0即为任一点（x0，y0）的岩层属性值。

2．2 研究实例

选择某一待预估节点的2 000m×2 000 m平面矩形区域作为插值区域。区域中应包含100个同类型离散插值采样点及其相关属性。对于区域中100个离散插值采样点 Bi，j＝（xij，yij），i，j＝1，2，3，…，9，结合相应的已知岩层属性值tij，构造相应的插值采样结点 Pi，j＝（xij，yij，tij），i，j＝0，1，2，…，9。利用多步迭代属性插值公式，可解方程求出任一点（x0，y0）的岩层属性值t0，并作出预估曲面模拟结果，如图1所示。

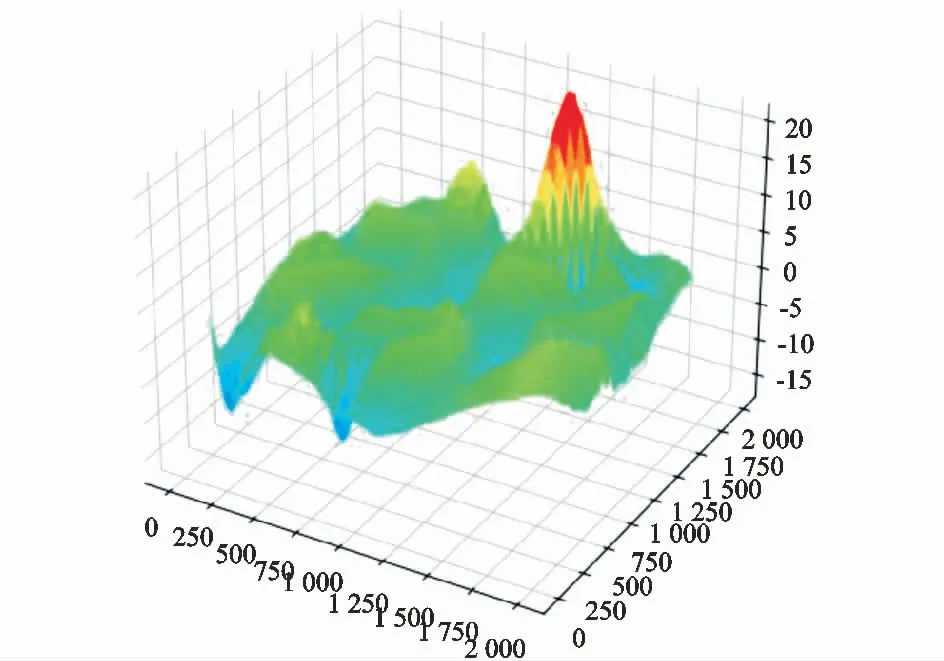
图1 多步迭代插值曲面Fig．1 M ulti-step iterative interpolation surface

2．3 本文方法与常见算法的对比分析

文献［1］在三维空间中利用反距离加权插值算法和基于B样条插值算法进行属性插值建模实现；文献［8］说明滑动克里金算法无法在完成四维属性数据体插值。文献［15］将基于距离场的三维空间属性插值方法应用于某铜矿区的可控源音频大地电磁法剖面数据，插值得到三维空间的视电阻率场。结合已有算法的解决方案，将各方案进行对比，结果见表1。

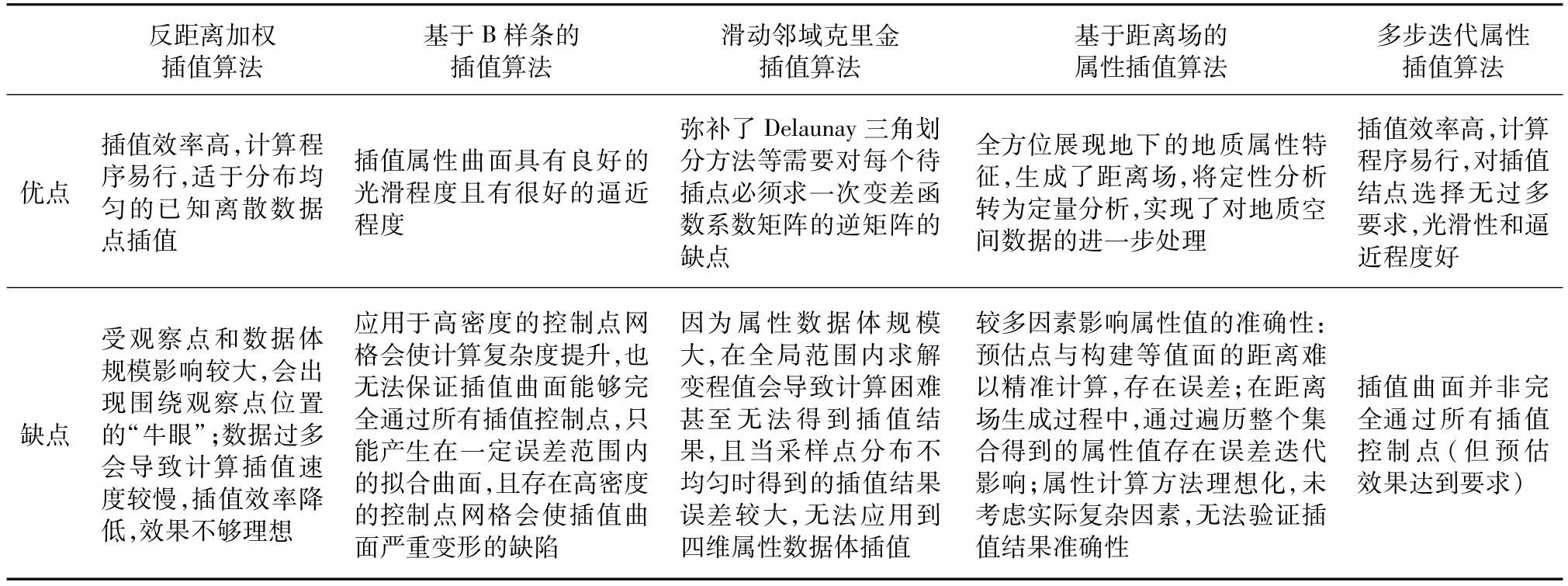
表1 5种预估方案效果对比Tab．1 Com parison of five estimation schemes

3 结 论

通过分析对比已有空间岩层属性的预估计算方法，本文提出了一种基于多步迭代属性插值算法，该方法适用于三维空间岩层属性插值预估问题。首先，通过选择插值区域，生成插值结点；其次应用多步迭代属性插值，最终达到计算预估点属性值的目的。基于此可以计算机构建三维空间岩层属性模型。本文算法方案对预估计算方法适于计算机实现，可提高预测的准确度，降低计算复杂度，是地层勘探与岩层属性研究的可行的有效途径。论文研究为进一步三维空间属性建模提供了新的思路和方法。