立德树人视角下的解题教学探讨*
2022-12-04广东省高州市教师发展中心陈应全
广东省高州市教师发展中心 陈应全
广东高州中学 胡 燕 邓火金
1 问题提出
教育部于2014年发布了《教育部关于全面深化课程改革落实立德树人根本任务的意见》,提出“立德树人”是教育的“根本任务”.高考始终坚持以价值为引领,确保立德树人在高考中的落实力度和落实效果,确保高考评价的正确方向.可见,“立德树人”已经从国家人才培养、人才选拔层面进入了高中教育.高中学科教学是实现立德树人的重要载体,也是立德树人的重要途径.因此,数学作为中学阶段的重要学科,自然也承载着立德树人的重任.
解题教学作为高中数学教学的一种常规教学模式,它对巩固基础知识、渗透思想方法、发展核心素养等有着不可或缺的作用,更是落实立德树人根本任务的一个重要契机.事实上,不少教师在解题教学中过分关注学生思维能力的培养以及解题技巧的传授,淡化了对学生德育方面的思考,这样的教学观念无疑有悖于国家立德树人的教育战略目标.那么在高中数学解题教学中如何落实立德树人根本任务呢?张奠宙教授在《数学学科德育》中指出:数学德育内容概括为三大类即理性精神、人文精神、道德品质.鉴于数学在形成人的理性思维、科学精神和促进个人智力发展方面有着不可替代的作用,因此,笔者认为在高中数学解题教学中立德树人的着力点应该放在理性精神与人文精神上.下面结合教学实践探讨在立德树人视角下的解题教学,以期抛砖引玉.
2 教学探讨
2.1 渗透文化,坚定学习信念
在教学活动中,教师应有意识地结合相应的教学内容,将数学文化渗透到日常教学中[1].事实上,很多数学问题都蕴涵着丰富的数学文化,只要教师平时注意积累相关素材,在合适的时候就会有用武之地.在解题教学中,不应只由枯燥的逻辑证明、成堆的模仿练习充斥着课堂.比如,教师可以结合例题渗透与题目有关联的数学史料,让学生了解数学家们的光辉事迹并体验问题的探究历程,从而提高学习兴趣,端正学习态度,坚定学习信念.
例1已知0 (2)说明上述不等式的几何意义. 例1来源于人教版(2019年版)选择性必修1第80页第17题.笔者将例1作为向学生渗透数形结合思想的重要案例.经过点拨后,很多学生都找到了解题思路,此时笔者顺势介绍了华罗庚先生写的一首关于数形结合的词:数与形,本是相倚依,焉能分作两边飞……,特别提到华老卓越的成就和自学成才、身残志坚以及爱国情深等感人故事,让学生对数学大师产生敬仰之心,更让学生领悟到人生道路上没有一帆风顺,必须经过千锤百炼,才能成为真正的国家栋梁之才;以后不管走到哪里,都要有胸怀祖国、立志报国的爱国情怀.华老的感人事迹激励着学生奋进,进一步坚定了他们努力学习的信念.事实证明:数学家们的奋斗经历对学生的成长发挥着巨大的“正能量”作用. 新高考甄选人才突出了立德树人的核心标准,即通过高考的考查,使具备较高政治觉悟、高尚道德情操和优秀意志品质的学生脱颖而出.爱因斯坦说:“优秀的性格和钢铁般的意志比智慧和博学更为重要.”具备坚韧的意志更是高中生早日成才的重要条件之一.事实上,受高中数学学科特点以及新高考人才选拔要求的影响,学生在学习数学的过程中更易遭遇困难与挫折.不少学生遇到难度稍大的题目往往感到恐惧,甚至抱着直接放弃的心态.但是困难永远都是磨炼意志的磨刀石,在解题教学中,教师应参照学生的认知水平以及教学内容的要求,有意识地筛选一些具有挑战性的题目,为他们创造“跳一跳,摘到果子”的机会并指导学生克服、战胜它,使他们逐步具备独立面对困难、征服困难的勇气,磨炼坚韧意志. 例2(2018·全国卷Ⅲ理21)已知函数f(x)=(2+x+ax2)ln(1+x)-2x. (1)若a=0,证明:当-1 (2)若x=0是f(x)的极大值点,求a. 鉴于每年高考导数压轴题难度较大,运算过程繁杂,为此笔者在高三复习导数时根据教学需要,常常选用难度较大的高考导数真题作为例题,引导学生深入分析并化解难点、攻克难题. 高考压轴题虽难,但也不是高不可攀.在解题教学中,教师应做到因材施教并为学生搭建合理、不断向上攀爬的“脚手架”,适时地唤醒学生头脑中储备的知识和经验,让这些知识和经验与题目取得联系并恰当化归,以便寻找到解题突破口.此外,当学生在学习上遇到困难时我们要多鼓励多引导,促使他们形成不畏辛苦、坚持不懈的良好品质,让他们做一个永不言败的坚守者.学生具备了这些特质,方可从容应对生活中可能出现的困难与挫折. 高考评价体系“四层”考查内容中,道德品质和综合素质是核心价值的重要内涵之一.它涵盖着责任担当等五大指标,要求学生立志肩负起实现中华民族伟大复兴中国梦的时代重任.因此,增强责任意识是落实立德树人任务的重要抓手之一.数学来源于生活,又高于生活,在解题教学中,教师应紧密联系生活实际,有意识地选取具有浓厚时代气息和鲜明中国特色的问题情境作为题材,将德育内容和题目内容有机融合,为树立责任意识营造氛围. 例3(2021·北京卷18)在核酸检测中, “k合1” 混采核酸检测是指:先将k个人的样本混合在一起进行1次检测,如果这k个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束;如果这k个人中有人感染新冠病毒,则检测结果为阳性,此时需对这k个人中的每个人再进行1次检测,得到每人的检测结果,检测结束. 现对100人进行核酸检测,假设其中只有2人感染新冠病毒,并假设每次检测结果准确. (Ⅰ)将这100人随机分成10组,每组10人,且对每组都采用“10合1”混采核酸检测. (ⅰ)如果感染新冠病毒的2人在同一组,求检测的总次数; (Ⅱ)将这100人随机分成20组,每组5人,且对每组都采用“5合1”混采核酸检测.设Y是检测的总次数,试判断数学期望E(Y)与(I)中E(X)的大小.(结论不要求证明.) 面对当前愈加严峻的疫情防控形势,我们要积极配合国家打赢这场防疫“攻坚战”.为此,笔者在随机变量综合应用中选取了与抗击新冠疫情密切相关的题材作为例题,让学生通过这些题目的解答,强化他们学以致用的意识,全面综合发展学生核心素养水平,借此让他们了解医务工作者进行核酸检测的流程,引导学生关注国家当今形势并积极执行国家防疫政策,以此增强学生的责任意识. 爱因斯坦说:“对真理与知识的追求并为之奋斗,是人类最高品质之一.”求真精神是一种不懈地追求真理的精神,它是数学精神乃至科学精神的核心与精髓,并教育人们客观公正地看待问题,不迷信权威,不迷信书本,具备批判性思维、创新思维.英国著名哲学家维特根斯坦说:“要让人相信真理,仅仅说出真理是不够的,人们还须找到错误到真理的道路.”因此,在解题教学中,教师要重视学生的错解,尝试引导学生深入剖析并弄清错因,让他们在“做中学”“错中学”“挫中学”,借此给予启迪与熏陶,使他们自身的内涵和素养得到提升的同时,达到弘扬求真精神之目的. 这是人教版普通高中教科书(2019年版)数学必修第一册第229页第4题.在教学中,笔者发现不少学生有如下的做法: 这种做法看似比较简洁易懂,结果也正确,但是笔者发现不少学生看到结果正确之后,不再研究解答过程是否有不严谨之处,这是欠缺反思意识与求真精神的表现.事实上,上述解答过程存在明显漏洞.笔者借机引导学生反思错解中的不妥之处,下面是一段教学实录: 师:这位同学做法简洁易懂,但解答过程严密吗?请同学们发表一下看法. 师:你可以帮他分析不妥的原因吗? 生2:可以!因为A的范围未能确定,所以cosA的正负还不能确定, 师:那如何分析呢? 生3:要对A的范围进行讨论. 师:生3做得很好,思维也很严密.我们在利用同角三角函数的关系式求解时,三角函数值的正负由角的范围确定. 在解题教学中,我们要有容许学生犯错的胸怀,重视对错解的剖析,让学生吸取深刻教训,实现“吃一堑,长一智”.这样的教学对培养学生严谨的科学态度与求真精神的作用无疑是巨大的. 罗素曾说过:“数学,如果正确看待它,不但拥有真理,而且也具有至高无上的美.”数学美包含对称美、简洁美、奇异美、统一美等.数学教学的审美教育目的在于培养、发展学生的数学美感,提高学生的审美情操[2].解题教学是教师渗透美育的绝佳时机,在审美视角下追求条件的转化、式子的恒等变形与解题路径的探寻等,这种寓美于教的方式有助于启迪学生的思维,从而快速找到解题突破口,彰显了美的魅力.此外教师应引导学生感受、领悟数学美,培养学生对数学美的鉴赏能力. 所以2S=2×2 018,即S=2 018. 在本例中,数式的“对称美”在探求解题思路的过程中起到了关键作用. 这是人教版普通高中教科书(2019年版)数学必修第一册第255页第18题. ① 从以上分析可见,三角函数化简中的关于函数名称、角度与结构的统一,即“统一美”,它在解题思路的探求过程中的作用不容低估.在解题教学中,我们在合适的时机可从审美视角引导学生分析题意,启发思考.学生则通过认识数学美,领悟美的真谛并形成美的数学思维方法,往往就能打破思维定式,另辟蹊径,找到最佳解题方案. 任何学科教学都是一种教育,都是有价值的教育,失去了教育、失去了教育的教学都不是真正的教学[2].总之,数学解题教学,从数学教学而言以提升学生核心素养为导向,以培养学生进一步学习所必需的数学知识、技能、思想和方法为基本目标已是无可厚非,但是从数学教育而言,还应将立德树人理念的渗透作为重要的教学内容,进一步明确落实立德树人根本任务的可行路径,培养学生的理性精神和人文精神,助推学生形成良好的道德品质,从而加快落实立德树人的根本任务.2.2 因材施教,磨炼坚韧意志

2.3 联系实际,增强责任意识
2.4 剖析错解,弘扬求真精神
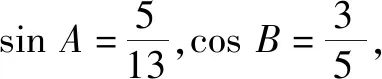


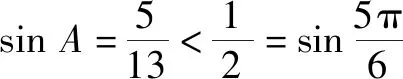

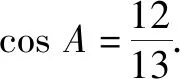
2.5 寓美于教,提高审美情操

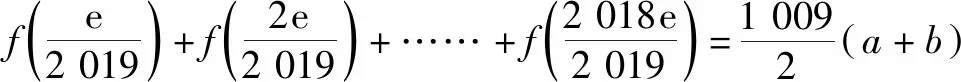
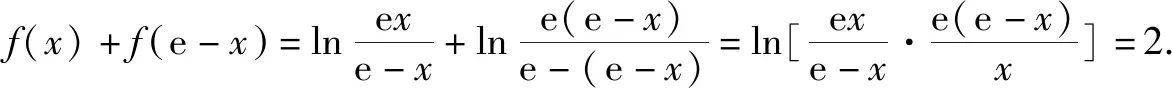
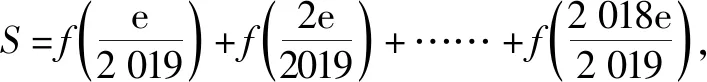
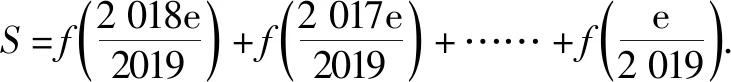






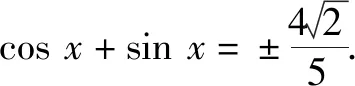


3 结束语
