理解教材编写意图，重构思维深层参与的教学设计*——以“余弦定理”为例

太原师范学院 王燕荣 王佳丽 陈 莉 闫喜红

1 问题的提出

余弦定理是高中数学的重要内容，其定量刻画了三角形边角之间的关系.《普通高中数学课程标准(2020修订版)》明确要求：借助向量的运算，探索三角形边长与角度的关系，掌握余弦定理，能用余弦定理解决简单的实际问题[1].其意在为向量的应用提供一个重要的载体，使学生进一步领悟向量法所蕴含的数学思想，掌握用向量运算解决几何问题的基本要领和方法的同时，完善对三角形的认知结构[2].

在余弦定理具体的教学设计中，多数教师存在认识上的误区和偏差.有些教师还是倾向于使用常规的证明方法，认为向量法只是附加品，“蜻蜓点水”说明即可；有些教师在原有证明方法的基础上增加了向量法，关注定理证法的多样化；还有些教师开门见山直接告知使用向量法证明，没有采取积极合理的方式促使学生有意识地运用向量法去解决问题，未能感受到向量法的巨大力量，没有凸显出向量法的特点和优势.

众所周知，数学教材是实现数学课程目标、保证数学教学实施的重要资源，是教材编写者集体智慧的结晶，体现了他们对数学及数学教学的认识、理解及价值取向.教师只有领悟和理解教材编写者的意图，学会创造性地加工和使用教材，才能避免陷入“完全脱离教材”和“照本宣科”的误区.

基于此，笔者以2019年人教版A版高中数学必修二第六章第4.3节“余弦定理”为例进行了教学设计，旨在加深学生对高中教材平面向量内容的理解，体会向量法的自然性和合理性，提升运用向量解决问题的意识和能力，进而获得良好的情感和认知体验，促进思维的深层参与，发展数学核心素养.

2 促进思维深层参与的余弦定理教学设计

2019年人教A版高中数学教材以余弦定理和正弦定理的证明为载体，创造更多的机会培养学生用向量法解决几何问题的意识，使学生切实感受到向量法解决问题的优势，更好地掌握向量法，也为后面学习正弦定理提供了方法上的引导.

在学习余弦定理时，无论以哪种方式证明，尽量以产生式的方法进行，尽可能使学生了解定理的由来、剖析定理的结构、探寻定理的证明思路和方法、熟悉定理的应用，构建系统化知识结构网络.

2.1 创设问题情境，引发学生学习需求

问题1大同市人杰地灵、风景优美，拥有许多驰名中外的名胜古迹，大同火山群是中国著名第四纪火山群.小明在寒假期间来到大同旅游，第一天他从大同火山群出发，向东偏南30°方向前进直线距离约4 km到达了阁老山.第二天计划从大同火山群出发，向东偏南85°方向前进直线距离约8 km就可以到达大同火山国家地质公园(如图1所示).小明改变了行程计划，想直接从阁老山出发到大同火山国家地质公园，如何行进最为合理？

图1 实际问题图

设计意图：从现实生活中的情境和学生已有的知识经验出发，激发学生学习和探究的热情，使学生经历分析、归纳、反思、修正的认识过程，引发思维积极参与，积累数学活动的基本经验.在此过程中教师不失时机地引导学生将生活问题数学化，发展数学抽象素养及分析和解决问题的能力，同时感受到家乡的美丽，增强对家乡的热爱之情.

2.2 重视启发质疑，探寻问题解决思路

问题2从阁老山B出发，只要求出BC的长度，一定能到达大同火山地质公园吗？

学生有些困惑，认为只要求出线段BC就解决问题了.教师借助《几何画板》作图，如图2所示.

图2 从阁老山行进BC长度的路线

学生观察图片可以发现，从阁老山B出发前进BC的长度能到达的地方有很多.

教师追问：仅仅通过求出两点间的距离，为什么不能确定目的地？

学生根据图2回答：因为方向不确定，还需要考虑前进的方向.

教师解释道：方向非常重要，大家都听过南辕北辙的故事吧！一旦方向错误，努力都是徒劳的.在这个问题中，既要考虑大小，又要关注方向，大家能想到什么？

学生马上想到前面刚学过的向量——既有大小又有方向.

设计意图：学生在思考过程中更多关注的是距离的远近，不易直接想到从向量的视角来解决问题.教师的启发引导和《几何画板》的动态展示，使学生感受到仅考虑距离(或路程)是不够的，自然联想到前面学习过的向量，激活解决问题思考的方向，提升思维的批判性和深刻性，潜移默化地让学生懂得努力重要但方向更重要的道理.

2.3 加强合作交流，促发学生深度思考

问题3使用向量法，如何解决问题2？从图3中能得到哪些信息？

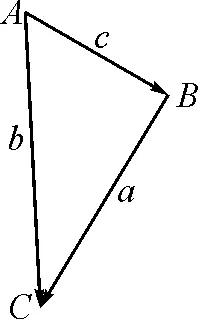
图3

=b2+c2-2bccosA.

同理可得

b2=a2+c2-2accosB，c2=a2+b2-2abcosC.

教师继续追问：长度问题已经解决了，方向呢?

设计意图：利用平面向量的有关知识，以问题为载体，通过教师提问、追问等方式，引导学生独立思考，探索并直观感知锐角三角形中边角之间的关系.抓住数学对象的本质特征，并体会向量法解决数学问题的优越性，增强运用向量法解决数学问题的意识，同时发展直观想象、数学运算和逻辑推理素养.

2.4 证明余弦定理，提升数学认知水平

问题4在锐角三角形中运用向量法证明了a2=b2+c2-2bccosA，那么在一般三角形中，是否也能得到类似结论？

学生自然联想到只需证明该结论在直角三角形和钝角三角形中成立即可.

图4

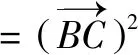
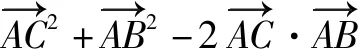
=b2+c2-2bccosA.

故a2=b2+c2-2bccosA.

图5

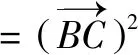
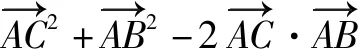
=b2+c2-2bccosA.

故a2=b2+c2-2bccosA.

师生共同概括余弦定理，剖析定理的条件和结论，强调数学语言之间的转化，并对定理变形，获得其推论:

设计意图：将问题从特殊情况推广到一般情况，实现了知识和方法的正迁移.通过文字语言，符号语言和图形语言的转化，使学生从多个角度理解余弦定理，提升思维的深度.学生在整个学习过程中感悟到从特殊到一般、分类讨论以及向量法的数学思想方法，体会到向量法的简洁以及余弦定理结构的统一美，进而发展逻辑推理和数学运算素养.

2.5 应用余弦定理，解决数学相关问题

问题5你能帮助小明解决遇到的问题吗？

由余弦定理，可以得到BC2=AB2+AC2-2AB·ACcosA.

由AB=4，AC=8，∠A=55°，得BC≈7.

故小明应从阁老山出发向西偏南59°前进7 km最快到达大同火山国家地质公园.

设计意图：应用余弦定理解决问题情境中提出的问题1，使学生体会到余弦定理是源于现实问题的需要，不是从天而降的，体现余弦定理的应用价值.通过解决实际问题培养学生的数学运算核心素养.

2.6 构建知识纵横联系，形成知识结构网络

问题6梳理本节课的学习过程，谈谈你有哪些收获？

图6

师生共同构建本节课知识结构网络(如图6)，促进学生知识的系统化.

设计意图：数学学习是不断形成新的数学认知结构的过程，良好的数学认知结构的形成是数学学习的关键.教师的主要任务是帮助学生建立知识间的纵横联系，构建数学知识的整体结构，促进学生数学认知结构的不断完善，从而提升数学思维品质.

3 结论

数学教材为“教”与“学”活动提供了重要的资源.教师要深入挖掘教材立意，体会教材编写者的意图，精准把握课程标准的要求，只有这样才能充分展示数学教材的引领和示范功效，从而创造性地使用教材，促进学生思维的深层发展及数学核心素养的落地.