指向高阶思维的初中数学解题教学
——以2021年苏州中考第18题为例
2022-12-04杨新芸
杨新芸 王 超
(盐城师范学院数学与统计学院 224002) (南京师范大学教师教育学院 210024)
近年来,高阶思维成为基础教育研究的热点.《义务教育数学课程标准(2022年版)》再一次强调了核心素养的培养,而高阶思维正是落实核心素养的重要途径.同时,数学解题教学是中学数学教学的重要组成部分,本文试图以一道中考数学题为例探究如何更好地开展指向高阶思维的初中数学解题教学.
1 高阶思维的内涵
所谓高阶思维,Resnick指出高阶思维是非算法的、复杂的,可能会产生多种解决方案,需要应用多种标准,自我调节,而且往往具有不确定性[1].钟志贤认为高阶思维就是发生在较高认知水平层次上的心智活动或较高层次的认知能力[2].布鲁姆的教育目标分类理论将认知领域分为知识、领会、运用、分析、综合和评价,而高阶思维在教学目标分类中表现为分析、综合、评价.段茂君、郑鸿颖等人认为高阶思维是指能够批判性、创造性地解决复杂问题并体现不规则性、复杂性、多样性、不确定性、自我调节性等特征的高水平心智活动[3].Hwang等人认为高阶思维包括批判性思维、创造性思维及问题解决能力三部分[3].Lewis等人认为高阶思维包括批判性思维、问题解决、决策、创造性思维等[4].另外,还有周莹等人认为数学高阶思维包括数学批判性思维、数学创造性思维、数学问题解决能力和数学元认知能力等[5].
下面,本文将从解题能力、创新性思维以及批判性思维等方面来探讨如何在初中数学解题教学中培养学生的高阶思维,希望能对初中数学教学有所裨益.
2 指向高阶思维的解题教学活动
例题(2021年苏州中考第18题)如图1,射线OM,ON互相垂直,OA=8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连结AB,AB=5,将线段AB绕点O按逆时针方向旋转得到对应线段A′B′,若点B′恰好落在射线ON上,则点A′到射线ON的距离d=.
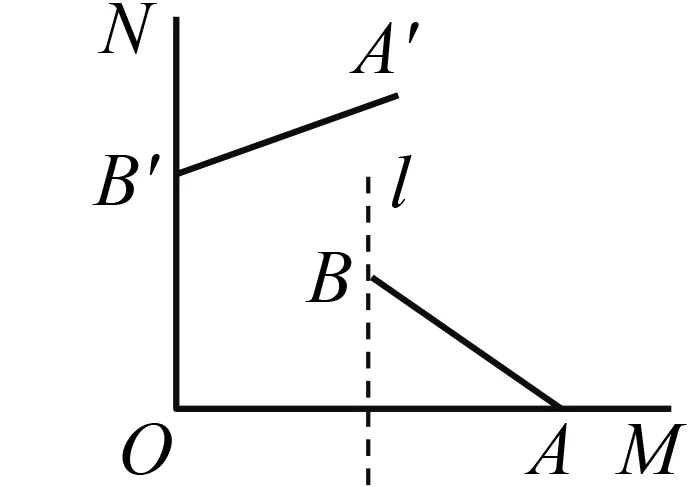
图1
2.1 搭桥建路 提高学生问题解决能力
学生在解决问题时常常会遇到思维障碍,教师自然不能直接呈现答案,而是应该建立起从问题到结论的桥梁,引导学生自己突破思维障碍,从题设条件走到解决问题的终点,从而提高学生分析问题、解决问题的能力.
问题1 旋转具有哪些性质?结合题图,我们可以得到哪些条件呢?(可以适当添加辅助线)
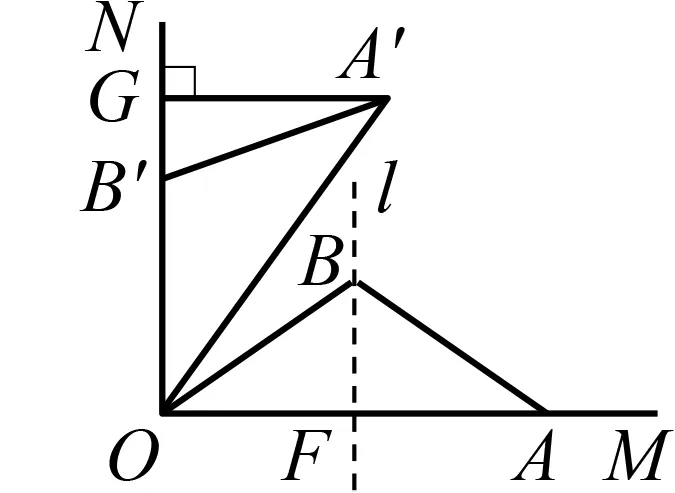
图2
分析 旋转不改变形状,故有AB=A′B′=5,由对应点到旋转中心的距离相等可知OA=OA′=8,OB=OB′,由任意一对对应点与旋转中心的连线所构成的旋转角相等可知∠AOA′=∠BOB′,等等.于是学生就自然而然地连结线段OB,OA′,这就构成两个新的三角形△OAB和△OA′B′(图2).
问题2 我们最终要求的是什么,在图中又可以怎样表示?
分析 题目要求的是点A′到射线ON的距离d.过点A′作A′G⊥ON,垂足为G,要求的距离d即为线段A′G的长度.
问题3 这时候图上有哪些特殊的图形,哪些又是与我们最终要求的结果相关的?
分析 其实图中的特殊图形很多:△OA′B′也可以通过△OAB旋转得到,所以二者全等;图中还有一系列直角三角形,进一步分析就可以发现这些直角三角形的对应角分别相等.结合我们要求的A′G的长度,可以发现A′G既可以看做Rt△OA′G的一条直角边也可以看做△OA′B′里边OB′上的高.
这三个问题的目的在于引导学生从题目所给的条件出发进行分析,然后从所要求的结果出发进行分析,最后综合对条件和结论的分析,建构从条件到结论的桥梁.这些问题也是一些比较通用的问题,对于其他问题的求解也具有一定的适应性,长期如此提问,学生可以逐渐内化问题串为自己的解题策略,在解决其他问题过程中能够对自己提出这类问题,从而自己搭建解题的桥梁,逐步提高自己解决问题的能力.
2.2 一题多解 培养学生创新性思维
教师要引导学生从不同角度多方位思考问题,培养学生的创新性思维.根据上面对题目的分析,可以从两个方向去思考:一是将A′G看做Rt△OA′G的一条直角边,二是将其看做△OA′B′中边OB′上的高.由此可以得到以下三种不同解法.
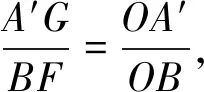
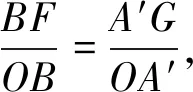
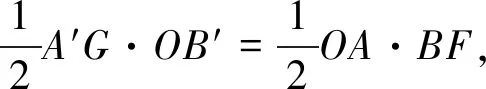
图3
一方面教师通过展示不同解法,鼓励学生不局限于一种方法解题,从多方面、多角度去看待问题,让学生发散思维.但另一方面要让学生明白这些不同解法之间并不是完全没有联系的,它们在本质上具有一致性.这道题的三种解法都归结于通过旋转的性质寻找相等条件,构造全等三角形.同时我们也要用批判性的思维去看待各种解法.例如,有学生构造了线段BF旋转后的对应线段B′H,通过射影定理或等积法求出点H到射线ON的距离HE,再通过中位线定理求得点A′到射线ON的距离(图3).不得不表扬学生是细致且全面地分析了题目中的条件的,但是对于条件与结论之间的本质联系还是理解得不够透彻,所以迂回地先去求了点H到射线ON的距离.
2.3 变式训练 促进学生的深层理解
通过一道题目的讲解让学生透彻领悟一个类型的题目往往很难.为了让学生更加深刻地感受线段绕线段外一点旋转的问题,就补充了变式1.
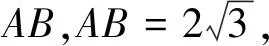

图4 图5
根据旋转添加辅助线OA′,OB,这样我们就又构成了两个全等三角形△OAB和△OA′B′.要求线段AB旋转时扫过的面积,也就是求图5中阴影部分的面积.通过割补可得到S阴影=S扇形OAA′-S△OAB+S△OA′B′-S扇形OBB′=S扇形OAA′-S扇形OBB′,从而由扇形面积公式就可计算出结果.但是这样的割补稍有一些复杂,学生可能会出现一些小问题.实际上我们可以把思路稍加转换:由于△OA′B′可以由△OAB得到,我们就可以将左上角的一小块阴影部分旋转到右下角(图6),这时候就很容易得到阴影部分的面积S阴影=S扇形OAA′-S扇形OCD.
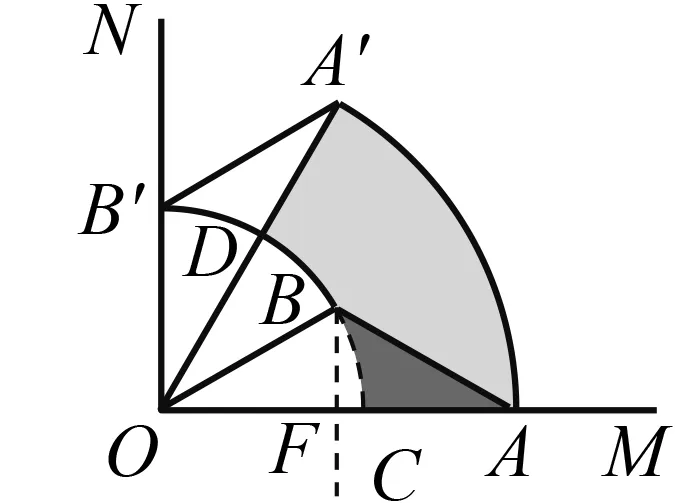
图6
变式2 在直角坐标系xOy中,A(3,4),B(6,-2),线段AB绕点O按逆时针方向旋转得到对应线段A′B′,使一端点正好落在y轴上,试求另一点的横坐标.
变式3 在直角坐标系xOy中,A(a1,b1),B(a2,b2),线段AB绕点O按逆时针方向旋转得到对应线段A′B′,使一端点正好落在y轴上,试用a1,b1,a2,b2的代数式表示另一点的横坐标.
变式2和变式3是在直角坐标系的情境下考虑原题的一般化,题目中没有明确指出旋转之后哪个端点落在y轴上,需要分类讨论.变式2探究的是线段AB与x轴相交的情况,变式3则是将线段AB更加一般化为任意的线段,解题所需的思维层次也更高.在这样的情况下,我们依然可以类比之前的方法,将A′G看做△OA′B′中边OB′上的高,通过等积法进行求解.
2.4 解题反思 培养学生批判性思维
解题后进行反思,这是学生应该养成的好习惯,所以在解题教学的最后也要及时引导学生进行批判性的反思.一方面是要让学生对自己、对他人进行批判[6],也就是用批判性的眼光对自己以及同学的解题过程进行思考;另一方面也是引导学生从多个角度、多个方面对整节课的内容进行反思总结,促进学生更好地完善自己的认知结构.下面是针对例题的教学提出的一系列的反思型问题:
问题1 解决上面一系列问题的过程中我们运用到了哪些知识和解题方法?
问题2 我们是怎样对题目进行思考分析的?
问题3 在解决问题的过程中大家都出现了哪些错误?如何避免出现这些错误?
问题4 在自己解题的过程中你遇到了怎样的障碍?又该如何突破这样的障碍?
其中问题1和问题2是对这节课内容的总结与反思,加深对所涉及的旋转、全等和相似、三角函数等知识以及这些知识之间联系的印象,对等积法、割补法等解题方法以及解题策略进一步回忆、整合,使学生能够较好地将知识串联起来,完善自己的认知结构.问题3和问题4则是对自己以及对他人的批判,批判性地反思在解题过程中出现的问题和困难,进一步梳理如何在下次解题的过程中避免出现这样的问题,突破这样的障碍.
3 指向高阶思维的解题教学的几个注意点
数学教学不仅要让学生掌握知识与技能,更重要的是要让学生在学习过程中增长智慧[7].所以在指向高阶思维的数学解题教学中还有以下一些要注意的问题.
3.1 教学内容重构
数学解题教学不应该只是简单地将学生需要讲解的题目按序号一一进行讲解,教师应当在解题教学前做好充足的准备工作.一方面,要将所要讲解的题目进行深入的剖析.同一章节的题目会侧重不同的知识点,同一知识点下的题目会涉及不同的解法,不同章节的题目也可能具有相同的解题思路.教师要做的就是将这些题目分类以及串联,将同一类型的题目放在一起讲解.另一方面,要适当拓展题目.有时仅凭一两道例题难以使学生真正领悟某一类题型或者某一种思想方法的本质,需要适当增加一些不同情境、不同思维层次的变式练习,这样才能使学生得到能力上的锻炼.
3.2 课堂需要通过开放性问题串联
传统的课堂提问更倾向于采用封闭的、单一的、指向性明确的问题.在数学解题教学的课堂中,很多教师也都习惯性地把解题过程拆成细碎的小问题,例如“题目中已知AB=OB,那么△OAB是什么特殊三角形呢?”这种问题学生不需要多加思索就能脱口回答,于是整道题的教学过程无比顺畅,学生对每一个问题都能轻松回答,但再次遇到这一类的问题时学生还是束手无策.所以指向高阶思维的数学解题课堂需要用开放性问题代替封闭式问题[8].开放性问题不是学生用一个字、一个词就能简单回答的,它需要学生经历一定的思考、推理.并且部分问题应该具有一般性,能够使学生将其逐渐内化为自己的解题策略或者一种解题思路.
3.3 教学需要培养学生自我分析评价的能力
在进行解题教学前,教师可以先制作一张错题分析表,大致如表1所示.
表1 错题分析表
让学生在课前进行自我分析评价、尝试完成此表.经过教师的讲解后,进一步补充、完善此表.通过此表,学生可以更加清晰地了解自己欠缺的知识以及未能完全掌握的方法.
