沥青混合料动态黏弹性分数阶导数Zener模型Wicket方法

杨胜丰，颜可珍，查旭东，黎国凯

(1. 广州市中心区交通项目管理中心， 广东 广州 513003；2. 湖南大学 土木工程学院，湖南 长沙 410082；3. 长沙理工大学 交通运输工程学院，湖南 长沙 410004)

0 引言

沥青混合料的动态力学性质跟温度和荷载作用时间密切相关，是一种典型的黏弹性复合材料[1-2]。因此，无论是路面力学研究，还是国内外的沥青路面设计规范，其材料力学参数均由静态向拟静态参数过渡[2-3]。为了克服数学模型描述黏弹力学信息的不足，研究者通常采用力学模型描述沥青混合料的黏弹力学性质[1，4]。然而，经典的黏弹力学模型描述动力学性质时，存在参数过多、过度拟合的现象[5]。

为了更好地描述沥青混合料的动态力学性质，研究者采用含参数较少经验模型描述沥青混合料的黏弹函数主曲线[6]。ZHAO[6]等建立了基于MHN模型的黏弹函数主曲线，该模型能够较好地描述动态模量、相位角和损失模量等黏弹参数。以上研究仅限于黏弹参数的表征，仍为经验模型，其复数模量推导并没有从数理方程出发。近年来，研究者采用黏弹性分数阶导数模型表征橡胶、高分子材料的力学性质，并取得了许多有价值的成果[7]。分数阶导数黏弹性模型是采用分数阶导数弹壶替代经典力学模型中的黏壶所得到的力学模型。许亚男[8]采用分数阶导数模型表征沥青的宽温宽频范围内的黏弹力学性质；颜可珍[9]等基于四参数分数阶导数模型微分方程建立了沥青混合料动态黏弹力学性质的五参数分数阶导数模型。以上研究构造分数阶导数模型主曲线时采用直接法，该方法因数值拟合过程中需要考虑移位因子的参数，所以模型参数较多。Wicket图方法是测试值和预测值在双对数坐标系内的图像呈现倒“U”型特征的作图方法，LEVENBERG[10]采用Wicket图方法得到了沥青混合料的动态模量和相位角主曲线。

为更好地推广和应用分数阶导数模型，本文基于四参数分数阶导数Zener模型(Fractional Derivative Zener Model， FDZ)模型微分方程，推导得到损耗因子与存储模量之间的函数关系式，并采用Wicket方法建立沥青混合料FDZ模型的黏弹函数主曲线，并与Sigmoidal模型进行了对比研究。

1 分数阶导数Zener模型

根据文献[9]，FDZ模型本构微分方程为:

(1)

式中：α为微分的阶数，0<α<1，E0为频率趋近于0的存储模量，称为静态模量，MPa；E∞为频率趋近于无穷时的模量，称为玻璃态模量，MPa；τ为特征时间。

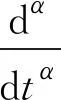
σ(iω)+(iωτ)ασ(iω)=E0ε(iω)+

E∞(iωτ)αε(iω)

(2)

整理得复数模量解析式为式(3):

(3)

分离实部和虚部分别得到存储模量式(4)、损失模量式(5)和损失因子(6)：

(4)

(5)

(6)

其中,ωn=ωτ为归一化频率；tan (δ)为损耗因子，δ为相位角，rad。

根据式(4)～式(6)可知，损耗因子与存储模量之间的关系式为式(7)

(7)

式中：E0≤E′(ω)≤E∞，从式(7)中可知，损耗因子是存储模量的函数，不含有参数τ，参数仅有3个(Ε0、Ε∞、α)，因此，损耗因子是与τ无关的函数。

2 主曲线构造

沥青混合料的黏弹力学特性跟温度和频率密切相关，具有典型的时-温等效性质，因此，基于该原理可以建立沥青混合料宽温宽频范围内黏弹函数主曲线，构造主曲线需要考虑移位因子、目标函数。

2.1 移位因子计算

本文采用WLF方程式(8)计算FDZ模型的移位因子。

(8)

式中:αT为温度移位因子，无量纲；T为试验温度，℃；T0为主曲线拟合时所选择的参考温度，℃；C1为常数，无量纲；C2为常数，℃。

缩减频率与角频率之间的关系为：

ωr=ω×αT

(9)

其中,ωr为角频率，rad/s。

2.2 目标函数

本文采用损耗因子作为拟合准则构造目标函数。

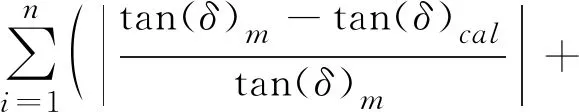
(10)

其中，fmin为目标函数最小值，tan(δ)m、 tan(δ)cal分别为损耗因子的测试值和预测值。

3 主曲线构造

3.1 wicket域主曲线构造

本文主曲线构造所采用的沥青混合料为AC-10和SMA-16，混合料动态模量试验数据出自文献[7]。 式(7)为损耗因子与存储模量之间的显示函数关系，在Wicket域内，损耗因子与存储模量之间仅与3个模型参数Ε0、Ε∞、α密切相关，与特征时间τ无关。假设τ=0.001 s时，通过优化公式(10)得到Wicket图， 如图1(a)所示。

从图1(a)可知，FDZ模型损耗因子的预测值与实测值吻合较好，拟合优度达到0.95，且得到FDZ模型参数分别为：E0=53.15 MPa，E∞=38 558 MPa，α=0.40，此时，动态模量主曲线如图1(b)中虚线所示。选择21 ℃为参考温度，通过平移得到参考温度下的动态模量主曲线，此时τ=0.000 79 s。

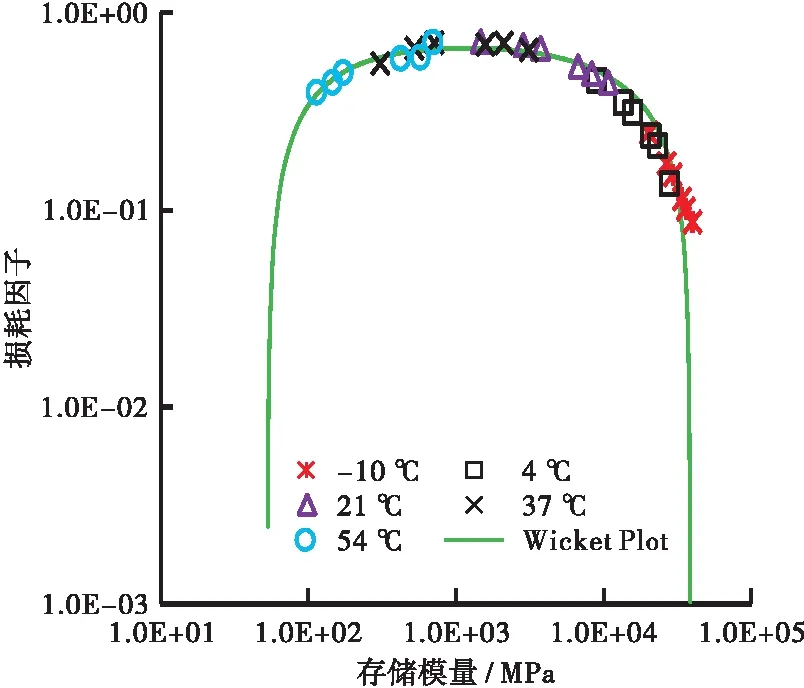
(a) Wicket图

为了建立参考温度为21 ℃时宽温宽频下的动态模量和相位角的主曲线，基于WLF方程式(8)，采用非线性拟合方法分别计算各个温度下的移位因子，并得到了动态模量和相位角的主曲线如图2所示。

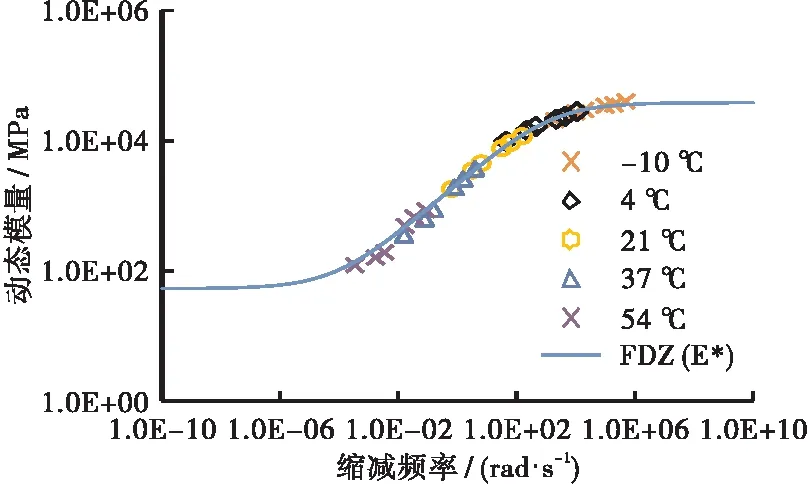
(a) 动态模量

上述采用Wicket方法建立FDZ模型动态模量和相位角主曲线的过程可以发现，相位角和动态模量主曲线均采用同一套模型参数，满足线性黏弹性Kramers-Kronig关系，通过优化得到的模型参数可以建立参考温度下FDZ模型频域或者时域内的本构微分方程。

模型拟合参数和各温度下WLF方程的参数分别如表1和表2所示。

表1 FDZ模型参数Table 1 FDZ model parameters沥青混合料E∞E0ατ0AC-1038 558530.407.90E-04SMA-1633 035680.39 4.60E-04

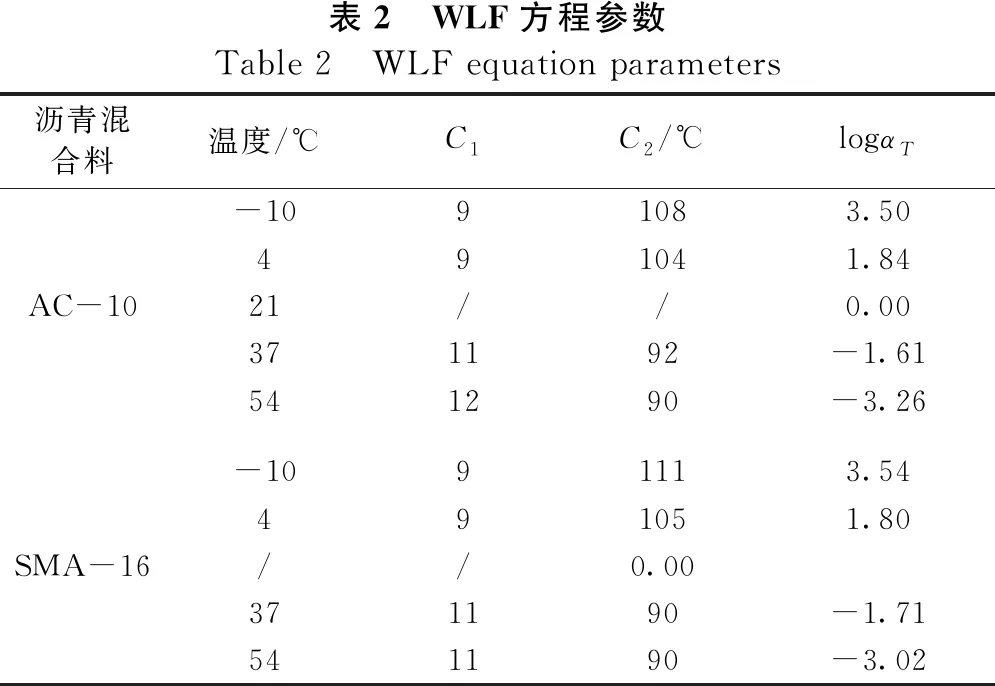
表2 WLF方程参数Table 2 WLF equation parameters 沥青混合料温度/℃C1C2/℃logαT-1091083.50491041.84AC-1021//0.00371192-1.61541290-3.26-1091113.54491051.80SMA-16//0.00371190-1.71541190-3.02

从表2中可知，Wicket方法各个温度下的C1和C2值均不同，与直接法采用同一套C1和C2值确定移位因子，存在明显的不同。

3.2 SWBZ与Sigmodal模型比较

美国公路合作计划项目提出采用Sigmoidal模型描述动态模量主曲线，该模型的解析式适用于动态模量和存储模量的表征[11-12]，其动态模量解析式为式(11)：

(11)

式中：a、b、c、d分别为模型参数。

采用非线性最小二乘法拟合得到的Sigmodal模型相位角测试值如图3(b)所示，Sigmodal模型和WLF方程的参数如表3所示。

从图3中可知，Sigmoidal模型能够描述单一的黏弹参数(动态模量)，但没有相位角的解析式，因而不能描述相位角的变化趋势；同样，该模型数值拟合过程中，仅考虑动态模量的影响，未考虑相位角的最优拟合，所以该模型不满足线性黏弹性的Kramers-Kronig关系。

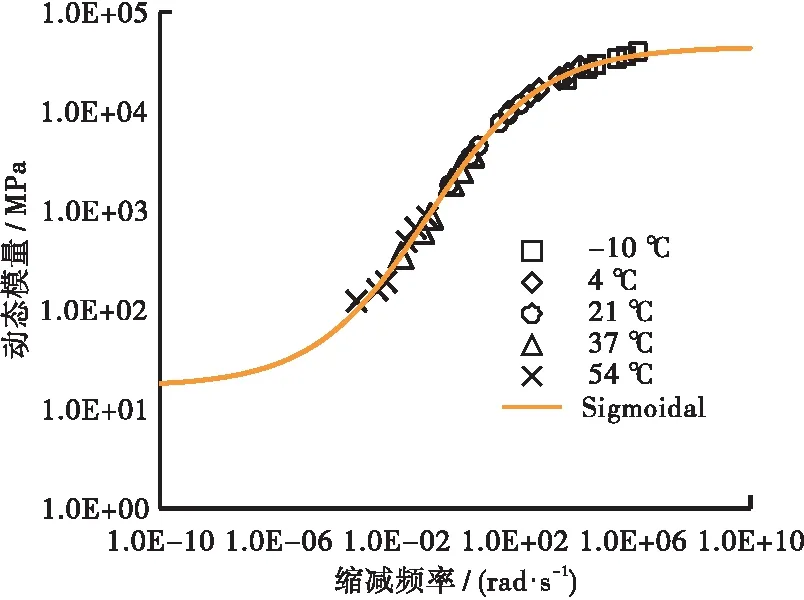
(a) 动态模量

表3 Sigmoidal 模型参数Table 3 Sigmoidal model parameters沥青混合料abcdC1C2/℃AC-103.42-0.48-0.511.2323212SMA-162.78-0.05-0.561.7618166

从图4可知，两种方法所得到的动态模量主曲线主要区别为高低频范围，中高频域内相差较小，低频范围内两种模型区别较大。从图5可以看出：两个模型移位因子[log(αT)]随着温度变化呈现直线特征，区别主要是在两端。低温处区别较大，高温处区别较小。Sigmoidal模型log(αT)更高，说明Sigmoidal模型高频移动的距离越大。综合图4和图5可知，低频时的预测曲线存在明显的区别，主要是两个模型低频范围内的预测曲线均由各自的模型参数值确定。

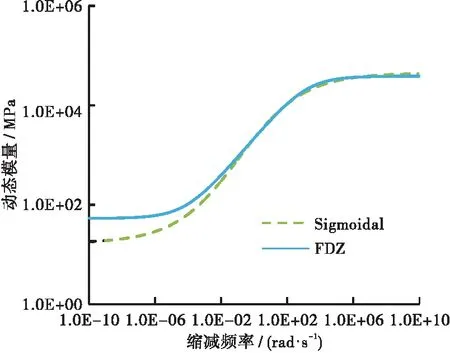
图4 AC-10沥青混合料不同模型动态模量主曲线

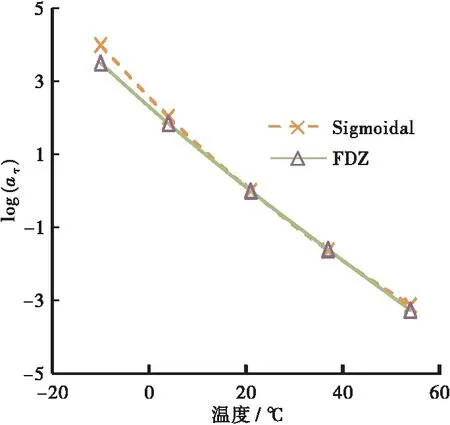
图5 AC-10沥青混合料FDZ模和Sigmoidal模型移位因子对比

综合图3～图5可知，虽然FDZ模型和Sigmoidal模型的移位因子区别很小，但是相比Sigmoidal模型，FDZ模型采用一套模型参数描述所有黏弹函数主曲线，满足线性黏弹性Kramers-Kronig关系。FDZ模型具有wicket域的显示函数关系式，采用非线性最优方法确定模型主要参数仅3个，准确性更高。

4 结论

本文基于FDZ微分方程式，通过傅里叶变换，得到了FDZ模型复数模量解析式，并进一步得到了该模型Wicket域内的解析式，采用两种常见的沥青混合料构造了FDZ模型黏弹参数的主曲线，并与Sigmoidal模型主曲线进行了对比研究，结论如下：

a.基于FDZ模型各黏弹参数之间的关系，得到了损耗因子与存储模量之间的显式函数关系式，并建立了两种沥青混合料黏弹参数FDZ模型的Wicket图，预测值与测试值吻合较好。

b.采用非线性优化方法确定了Wicket域内3个与加载频率无关的模型参数E0、E∞、α；采用同样的方法确定了参考温度下的特征时间τ和WLF方程参数C1、C2。

c.与Sigmoidal模型不同，FDZ模型采用一套模型参数确定了沥青混合料的复数模量和相位角主曲线，满足Kramers-Kronig关系，其微分方程可为沥青路面层状黏弹性力学计算提供参考。