基于流固耦合的强度折减法的地下水渗流对隧道稳定性的影响研究

郑晓珣

(陕西铁路工程职业技术学院 高铁工程学院，陕西 渭南 714099)

随着有限元理论的快速发展，强度折减法在在岩土工程设计和施工应用中取得了广泛应用。众多学者对有限元强度折减法的破坏判断准则和工程应用做了大量的研究[1-4]。隧道工程在设计中通常采用半经验—半理论的经验方法，这种方法可以计算衬砌的内力和变形，但无法确定隧道围岩在何种情况下破坏，也无法确定隧道的潜在滑裂面和安全系数。

为获得隧道的极限破坏形态，一些学者尝试将临界滑动面的位置和形态[5-6]。文献[6]详细分析了有限元强度折减法用于计算隧道安全系数，确定将有限元强度折减法用于隧道工程中，指出有限元强度折减法不仅可以确定隧道的临界破坏面和安全系数，还可以根据破坏面和安全系数的大小判断设计的合理性。文献[7]采用隧道洞周围岩位移或塑性应变发生突变作为失稳判据，运用强度折减法计算了无衬砌和有衬砌2种情况下隧道的安全系数。隧道施工过程中经常伴有地下水渗流现象，地下水渗流引起的围岩大变形乃至失稳情况时有发生，这极大加剧了隧道施工中的风险。已有研究表明，隧道开挖和开挖引起的地下水渗流将引起围岩应力重分布，对隧道围岩的稳定性有重要的影响；地下水渗流使隧道围岩的位移、应力以及支护结构的内力有较大增长[8]。文献[9]利用数值模拟研究隧道开挖引起的渗流场，并对隧道涌水量进行预测。文献[10]利用轴对称解析法研究了不同渗透系数、注浆半径和衬砌厚度情况下隧道衬砌渗透量、内力、偏心距以及安全系数。文献[11]以实际工程为背景，采用流固耦合理论研究了海底隧道施工引起的围岩应力场、渗流场分布规律，研究结果表明地下水渗流对海底隧道围岩的变形和应力有较大影响。综上所述，目前关于强度折减法、地下水渗流的研究有很多，而关于地下水渗流对隧道稳定性影响的研究还很少。随着我国隧道工程的快速发展，有必要开展地下水渗流对隧道稳定性影响的研究。

综上所述，本文基于流固耦合的强度折减法来分析地下水渗流对隧道稳定性的影响。并对地下水渗流、流固耦合计算模式影响隧道安全系数进行详细分析，揭示地下水水位和隧道安全系数的内在规律。所得研究结果可为水下隧道的设计和施工提供一定的理论依据和指导。

1 基于流固耦合的强度折减法

1.1 强度折减法原理

在强度折减法计算分析中，利用式(1)对岩土体强度参数进行折减：

(1)

(2)

1.2 基于流固耦合的强度折减法的实现过程

隧道破坏大多属于剪切破坏，抗拉强度折减与否对隧道安全系数的影响很小[13]，本文只对隧道围岩抗剪强度参数c和φ进行折减，计算得到的安全系数为剪切安全系数。具体实现过程如下，在流固耦合分析之前利用折减后的围岩力学参数进行初始地应力平衡，并将计算得到的节点位移、速度以及塑性区进行初始化。随后调用渗流模式，围岩设为各向同性渗流模型，利用FISH语言编写程序对围岩渗透系数、孔隙率、流体模量、流体抗拉强度、流体密度，孔隙水压力进行赋值。通过钝化隧道单元模拟隧道的开挖，将隧道洞周边界孔隙水压力设置为0。随后开启渗流模式进行流固耦合计算。通过逐渐增大折减系数获得隧道特征点位移随折减系数的变化曲线；位移—折减系数曲线发生突变的位置所对应的折减系数即隧道的安全系数。

2 地下水渗流对隧道稳定性的影响

2.1 数值计算方案

利用国际通用岩土工程软件FLAC3D进行数值计算，FLAC3D不仅可以进行无渗流模式计算，还提供流固间接耦合和流固完全耦合2种模式进行流固耦合计算。为研究地下水渗流及流固耦合计算模式对隧道安全系数的影响，以圆形隧道为例，计算3种工况下隧道的安全系数(表1)。

表1 工况环境Tab.1 Working environment

2.2 数值计算模型

隧道围岩在纵向方向上所表现出的特征基本一致，为提高计算效率和精度，将隧道安全系数的求解按平面应变问题来处理。所建立的数值计算模型如图1所示，隧道断面为圆形，半径5 m，埋深45 m；模型共有1 984个节点，950个单元。为降低边界条件对计算精度的影响，X方向模型边界与隧道洞壁之间距离均取为50 m(5倍洞直径)，模型上边界和下边界到洞壁的距离均取为45 m(4.5倍洞直径)。

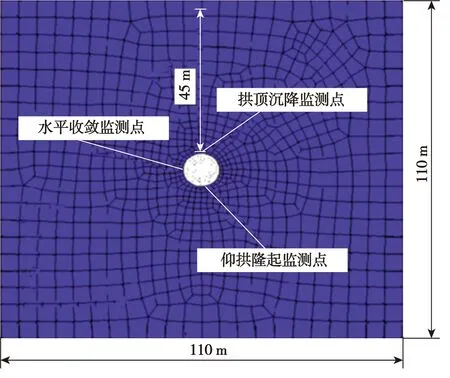
图1 数值计算模型 Fig.1 Numerical model

根据已有工程经验及地勘资料，数值模拟中所采用的围岩物理力学参数，见表2。模型应力及渗流边界条件为：模型顶端自由，固定相应水位孔隙水压力并施加相应应力边界条件；模型两侧面固定X方向水平位移，模型底部限制Z方向位移；模型两侧及底部均为透水边界。隧道开挖前围岩孔隙水压力为静水压力，饱和条件下围岩初始竖向应力和侧压力可由式(3)和式(4)求得：

σzz=ρsatgz

(3)

σxx=σyy=k0(ρsat-ρw)gz

(4)

式中，σzz为岩体竖向应力；σxx和σyy为水平应力；σzz为竖向有效地应力；ρsat为岩体饱和密度；ρw为水密度；g为重力加速度；k0为侧压力系数；z为计算位置处埋深。

然而，正当他想要细看的时候，师父推门而入，面色阴沉着收走了古卷。那时的他，真的很害怕师父那张骷髅脸，只战战兢兢地站起身，一句话也不敢说。师父或许是觉得他还是个孩子，于是在走到门口的时候，安慰了一句：“等你成为了真正的天葬师，才有资格看它。”

表2 岩体力学参数Tab.2 Rock mechanical parameters

2.3 数值模型有效性验证

围岩剪应变增量不仅可以用来确定隧道的安全系数，还可以确定隧道的潜在破坏面。折减系数为1.00和6.55时隧道围岩的剪应变增量云图如图2和图3所示。从图中可以看出，强度折减系数为1时，隧道剪应变增量沿隧道周围分布比较均匀，剪应变增量较小，最大值仅为2.26×10-4。当强度折减系数为6.55时，剪应变增量有较大增大，最大值位于隧道拱脚部位，其值为0.152；隧道围岩将沿着图3中所示临界状态滑动面发生失稳。从而验证了利用基于流固耦合理论的强度折减法求解隧道安全系数和临界破坏面的有效性和正确性。

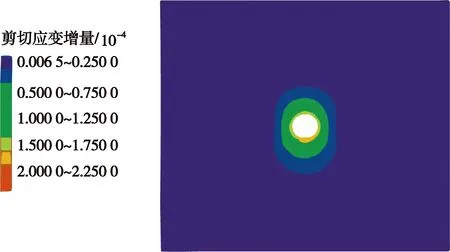
图2 折减系数为1时隧道围岩剪应变增量Fig.2 Shear strain increment of surrounding rock when reduction factor is 1

图3 折减系数为6.55时隧道围岩剪应变增量Fig.3 Shear strain increment of surrounding rock when reduction factor is 6.55

3 计算结果分析

通过逐渐增大折减系数对岩体力学参数进行折减，直到隧道洞周位移出现突变为止。数值模拟中记录隧道洞周围3个监测点。根据计算结果绘制隧道拱顶沉降、水平收敛、拱底隆起随折减系数的变化曲线，位移—折减系数变化曲线出现突变时所对应的折减系数即为隧道的安全系数。

3.1 工况1隧道安全系数

工况1为不考虑地下水的情形，利用岩体干密度计算初始地应力场。工况1隧道特征点位移随强度折减系数变化曲线如图4所示。

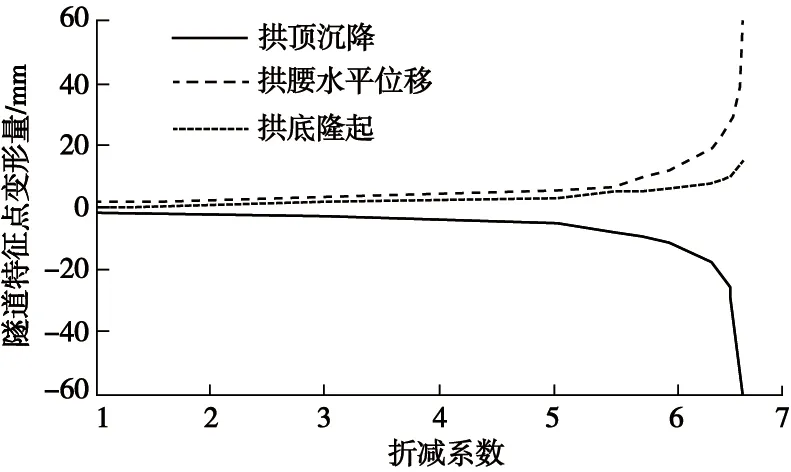
图4 工况1隧道特征点位移随强度折减系数变化曲线Fig.4 Curves of displacement with reduction factor in case 1

从图4可以看出，拱顶沉降与拱腰水平位移变化趋势基本一致，当折减系数大于6.55时围岩变形量急剧增大。因此，不考虑地下水情况下隧道安全系数为6.55。需要注意的是当强度折减系数大于6.55 时，隧道拱底隆起量并没有显著增大，这是由于临界状态时隧道将沿着图中所示的临界滑动面发生破坏。隧道拱底监测点在滑动面以下，受隧道失稳的影响较小，拱底隆起量增长量较小。

3.2 工况2隧道安全系数

工况2中采用流固间接耦合模式计算地下水渗流对隧道安全系数的影响。具体计算过程如下：首先开启渗流模式，并关闭力学进程，分析隧道开挖引起的渗流场变化。待渗流场计算完成后，关闭渗流模式，同时将流体模量设置为0(为避免力学计算引起孔隙水压的再次改变)，开启力学进程进行力学计算直至收敛。利用这种计算模式，孔压场不与应力场相耦合，是计算地下水渗流的一种近似计算方法。该工况下隧道特征点位移随折减系数的变化曲线如图5所示。对比图4和图5可发现，工况2中隧道变形趋势与工况1较一致。拱顶沉降和水平收敛均远大于拱底隆起变形量，且拱底隆起量随强度折减系数增长不明显。当强度折减系数大于5.23时，拱顶沉降和拱腰水平位移急剧增大，工况2中计算得到的隧道安全系数为5.23。

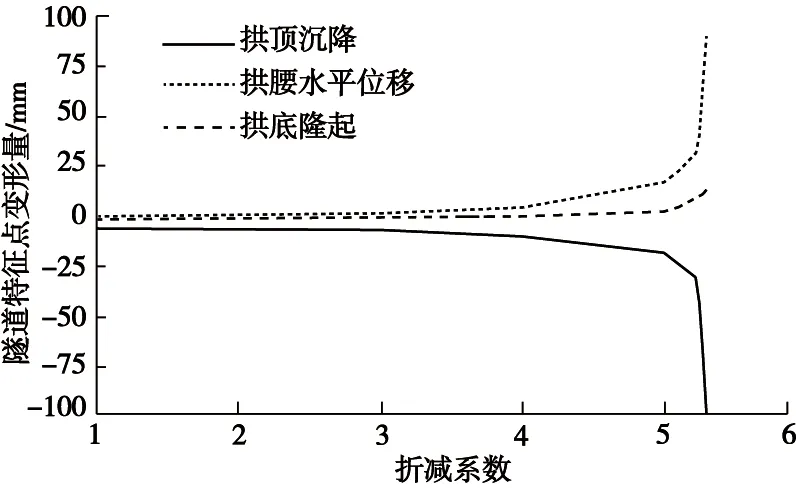
图5 工况2隧道特征点位移随折减系数变化曲线Fig.5 Curves of displacement with reduction factor in case 2

3.3 工况3隧道安全系数

工况3利用流固完全耦合模式计算地下水渗流时隧道的安全系数。利用流固完全耦合模式求解时，流体模式和力学模式均处于打开状态，直接进行流固耦合求解。这种求解方法中每个渗流时间步中都包含有若干个力学时步，每个渗流时间步中均要达到力学平衡，为了确保计算精度渗流时间步足够小，故需要耗费大量的计算时间。该工况下隧道特征点位移随折减系数变化曲线如图6所示。

图6 工况3隧道特征点位移随折减系数变化曲线Fig.6 Curves of displacement with reduction factor in case 3

从图6中可以看出，拱顶沉降和拱腰水平位移在强度折减系数大于5.1时急剧增大，该工况下隧道安全系数为5.1。

3.4 计算结果对比

为研究地下水渗流及流固耦合计算模式对隧道安全系数的影响。将3种计算工况下所求的隧道安全系数汇总于表3，以工况1的计算结果为基准计算工况2和3的相对变化量。从表3可以看出，工况2和3中隧道安全系数较工况1分别降低20.2%和22.1%。由此可见，地下水渗流将引起隧道安全系数显著下降。对比工况2和3计算结果可以发现，工况3计算结果要略小于工况2，这是由于工况2采用流固间接耦合模式，弱化了渗流场与应力场之间的相互影响。工况2和3计算模式的计算结果仅相差1.9%。由此可见，流固耦合计算模式对隧道的安全系数并无显著影响。然而，计算过程表明工况3所消耗的计算时间要远大于工况2。因而，在不显著影响计算结果精度的条件下，建议采用流固间接耦合计算模式计算地下水渗流情况下隧道的安全系数。

4 地下水水位对隧道安全系数的影响

上述计算结果表明地下水渗流对隧道安全系数影响较大。工程中地下水水位往往会发生变动，地下水水位变化引起水头差的改变，进而影响隧道的稳定性。为研究地下水水位对隧道安全系数的影响，采用流固间接耦合计算模式计算对地下水水位为-10、-20、-30、-40、-50 m时隧道的安全系数。地下水水位与隧道位置关系如图7所示，图7中以模型上表面为±0.000 m。

图7 地下水水位与隧道相对位置关系Fig.7 Relative position between groundwater level and tunnel

不同地下水水位时隧道拱顶沉降随强度折减系数变化曲线如图8所示。从图8可以看出，随着地下水水位下降，隧道安全系数有所增大。地下水水位处于模型上表面位置时，隧道安全系数最小，其值为5.23；地下水水位为-50 m时，隧道安全系数最大，其值为6.53。由3.1节计算结果可知，不考虑地下水时隧道安全系数为6.55。地下水水位-50 m时隧道安全系数与不考虑地下水时基本一致。由此可见，当地下水水位低于隧道拱顶位置时，地下水渗流对隧道安全系数影响很小。

图8 不同地下水水位时隧道安全系数Fig.8 Safety factor under different groundwater level

为揭示地下水水位与隧道安全系数之间的关系，绘制隧道安全系数与地下水水位的关系曲线，如图9所示，并对计算结果进行拟合。计算结果表明，隧道安全系数与地下水水位呈线性相关，地下水水位每降10 m，隧道的安全系数则增大0.26。因而，在富水地区进行隧道施工时，在不显著影响周围环境的条件下应尽可能地降低地下水水位，以提高隧道的安全系数。

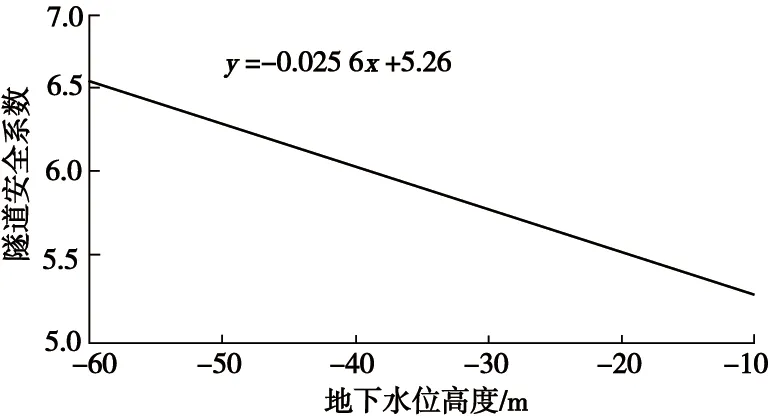
图9 隧道安全系数与地下水水位变化曲线Fig.9 Curves of safety factor with groundwater level

为研究隧道拱顶沉降随地下水水位的变化规律，利用流固间接耦合模式计算相同安全系数、不同地下水水位时隧道拱顶沉降，计算结果如图10所示。 从图10可以看出，折减系数相同时，拱顶沉降随地下水水位升高而显著增大；且折减系数越大，增大趋势越显著；隧道施工中应注意控制地下水渗流引起的围岩变形量增大。

5 结论

为充分研探讨地下水渗流对隧道稳定的影响，本文基于流固耦合的强度折减法优化计算隧道稳定性的安全系数，通过仿真计算获得以下结论。

(1)考虑地下水渗流情况下隧道安全系数降低，可作为影响隧道的安全系数的重要因素。隧道设计和施工中应予以考虑地下水渗流对隧道稳定性的影响。

(2)流固间接耦合模式和流固耦合模式的计算结果大致一致，但流固间接耦合模式计算消耗的时间短，可选取该方式对地下水渗流下隧道的安全系数进行计算。

(3)隧道围岩变形量随地下水水位升高而增大，安全系数却降低，且二者呈线性相关。在不影响地下水环境的情况下，应尽可能地降低地下水水位，提高隧道的安全系数。