基于复合材料理论的再生混凝土峰值应变模型

赵木子 ， 王玉银 ， 耿 悦

（1.中冶建筑研究总院（深圳）有限公司，广东深圳 518055；2.哈尔滨工业大学（深圳）土木与环境工程学院，广东深圳 518055；3.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江哈尔滨 150090；4.哈尔滨工业大学土木工程学院，黑龙江哈尔滨 150090）

通过调整混凝土配制时的用水量［1-3］、优化骨料颗粒级配［4-5］和添加钢纤维［6］等方式，可以有效降低再生骨料的影响，使再生混凝土（RAC）的性能满足建筑结构的要求.可靠的再生混凝土轴压应力-应变模型是进行再生混凝土结构设计的前提，而准确预测再生混凝土的峰值应变（峰值应力对应的应变）是建立该模型的关键.同时，再生混凝土的峰值应变也是评价其变形能力的重要参数，应予以研究.当再生骨料掺入时，由于表面存在残余砂浆，降低了再生骨料的刚度，使其对新砂浆变形的约束作用下降，峰值应变增大［7-9］.前期研究已发现，再生骨料表面残余砂浆的含量及制作再生骨料的原混凝土水灰比（基体混凝土水灰比）会影响骨料的刚度［2，10］，是峰值应变的关键影响因素.因此，在再生混凝土峰值应变模型中应考虑上述关键因素的影响.

为此，本文首先基于收集到的100 组再生混凝土峰值应变数据，充分论证传统再生混凝土峰值应变模型的局限性；随后，在复合材料模型的基础上，考虑再生骨料的影响，通过理论推导建立考虑残余砂浆含量及基体混凝土水灰比影响的峰值应变预测模型；最后，通过参数分析与试验数据对比，确定了形式较为简单且预测精度较高的预测模型.

1 传统再生混凝土峰值应变模型的局限性

目前，各国学者已考虑再生骨料掺入的影响，对再生混凝土峰值应变预测模型开展了研究，针对加载方式［11］、取代率［12-14］、骨料类型［15］、混凝土强度［16-17］、骨料碳化程度［18］和受火温度［19］等关键因素的影响建立了模型.研究中所采用的建模方法主要分为2种.一种是沿用现行规范中普通混凝土弹性模量模型的建模方式，以再生混凝土强度为主要参数，通过试验回归方法建立模型（如文献［11］）.这类模型公式简单，易于被设计人员采纳.另一种是以再生粗骨料取代率为主要参数（如文献［13，16-17］）建立模型.尽管现有文献显示前一种方法对各自的试验均具有良好的预测精度，但由于这类模型均基于有限的试验数据建立，试验数据参数范围较窄且各文献的试验参数也不相同，因此在预测较广参数范围内再生混凝土的峰值应变时可能具有局限性.

因此，本节将主要讨论现有建模方法在预测收集到的100 组较广参数范围峰值应变数据时的可靠性，为后文再生混凝土峰值应变模型的建立奠定基础.

1.1 与混凝土强度相关的模型

为评估传统混凝土峰值应变建模方法在预测再生混凝土峰值应变时的可靠性，对所收集到的12 篇文 献［5，7，9，15-17，19-24］中 100 组 再 生 混 凝 土 峰 值 应 变 εc0，r数据与混凝土28 d 圆柱体轴心抗压强度fcm28之间的关系进行分析，结果如图1 所示.图中所涉及的试件涵盖了工程中常见的再生混凝土参数范围：再生粗骨料取代率（质量分数，文中涉及的取代率、水灰比等除特别说明外均为质量分数或质量比）为0%～100%，再生细骨料取代率为0%～100%，残余砂浆含量为5.5%～40.0%，28 d 圆柱体轴心抗压强度为19.1～89.2 MPa.由图1 可以看出，具有相同圆柱体轴心抗压强度试件的峰值应变离散性较大.例如，当混凝土强度等级为C30 时，再生粗骨料混凝土峰值应变在（1 523～4 449）×10-6范围内波动，差异高达192%；再生细骨料混凝土峰值应变范围为（1 484～2 974）×10-6，差异为100%.造成该差异的主要原因在于再生骨料对混凝土强度与其对峰值应变的影响机理不同.具体而言，混凝土强度主要受有效水灰比及界面过渡区黏结性能的影响，目前大部分试验采用预吸水法或饱和面干法处理再生骨料，致使再生骨料内部的相对湿度高于新水泥浆，在混凝土拌和过程中，骨料内预吸附的自由水会向外扩散，从而增大混凝土的有效水灰比［2］；同时，再生骨料的掺入会降低骨料-新水泥浆间界面过渡区的黏结强度［8］.而再生骨料对峰值应变的影响主要体现在混凝土裂纹剧烈开展导致的砂浆变形提高以及骨料自身刚度的降低.此外，再生骨料影响机理的差异可导致再生骨料对混凝土 fcm28及 εc0，r的影响趋势不同 .例如，在文献［9］中，100% 掺入再生粗骨料将使 fcm28降低 6.5%，εc0，r提高20.2%.由于传统模型通常认为混凝土强度与峰值应变的变化趋势相同，因此采用传统建模方法无法准确预测再生混凝土的峰值应变，具有局限性.

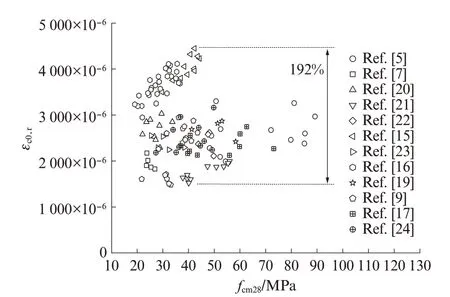
图1 再生混凝土峰值应变与强度的关系Fig.1 Relationship between εc0，r and fcm28 of RAC

1.2 与再生粗骨料取代率相关的模型

近年来，各国学者［13-19］以再生粗骨料取代率rC为主要参数，通过建立再生混凝土与同配比普通混凝土峰值应变之间的关系来量化再生骨料的影响.为分析该方法的准确性，对再生混凝土与同配比普通混凝土峰值应变的比值（εRAC0/εNAC0）同rC之间的关系进行对比分析，如图2 所示.图中所采用数据点的参数范围与图1 相同.由图2 可见，尽管以再生混凝土与同配比普通混凝土峰值应变之比来量化再生骨料影响的建模方式，可以在一定程度上降低试验结果的离散性（再生混凝土峰值应变试验结果离散性由192%下降至81%），但再生骨料的影响因素较多，仅以rC为主要参数建立模型仍无法准确描述再生混凝土的峰值应变，可能需要引入基体混凝土水灰比mWor/mCor、残余砂浆含量wRM等影响参数.例如，将文献［5，15，24］中基体混凝土水灰比与残余砂浆含量不同的典型试件试验结果进行对比，如图3 所示.

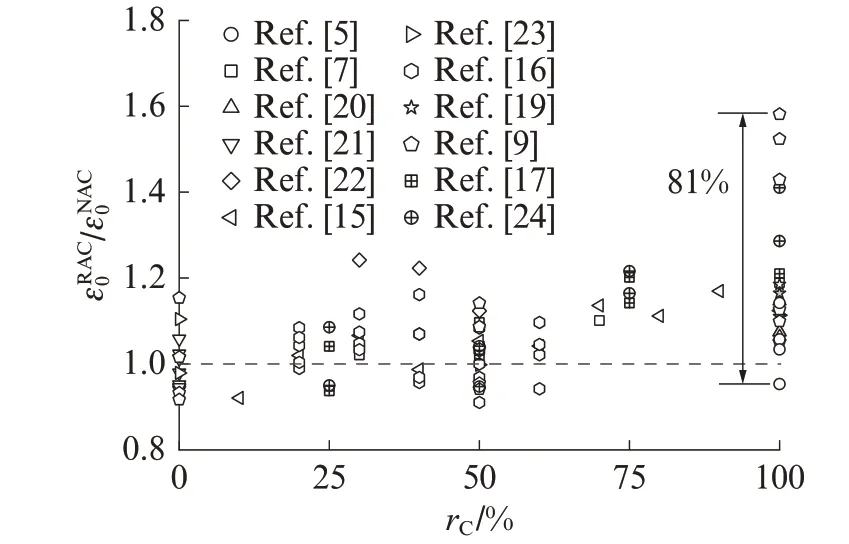
图 2 εRAC0 /εNAC0 与 rC的关系Fig.2 Relationship between εRAC0 /εNAC0 and rC

从图3 中可以看出：基体混凝土水灰比和残余砂浆含量也是影响混凝土峰值应变的关键因素，当基体混凝土水灰比从 0.56 下降至 0.28 时，εRAC0/εNAC0值可降低49%（图3（a））；当残余砂浆含量从5.5%提升至34.7%时，εRAC0/εNAC0随着再生粗骨料取代率的变化而显著变化，在再生粗骨料全取代条件下二者差异可达23%（图3（b））.造成该显著差异的原因在于基体混凝土水灰比的提高以及残余砂浆含量的降低均会使得骨料刚度减小，导致骨料对新砂浆变形的约束作用减弱，峰值变形增加.

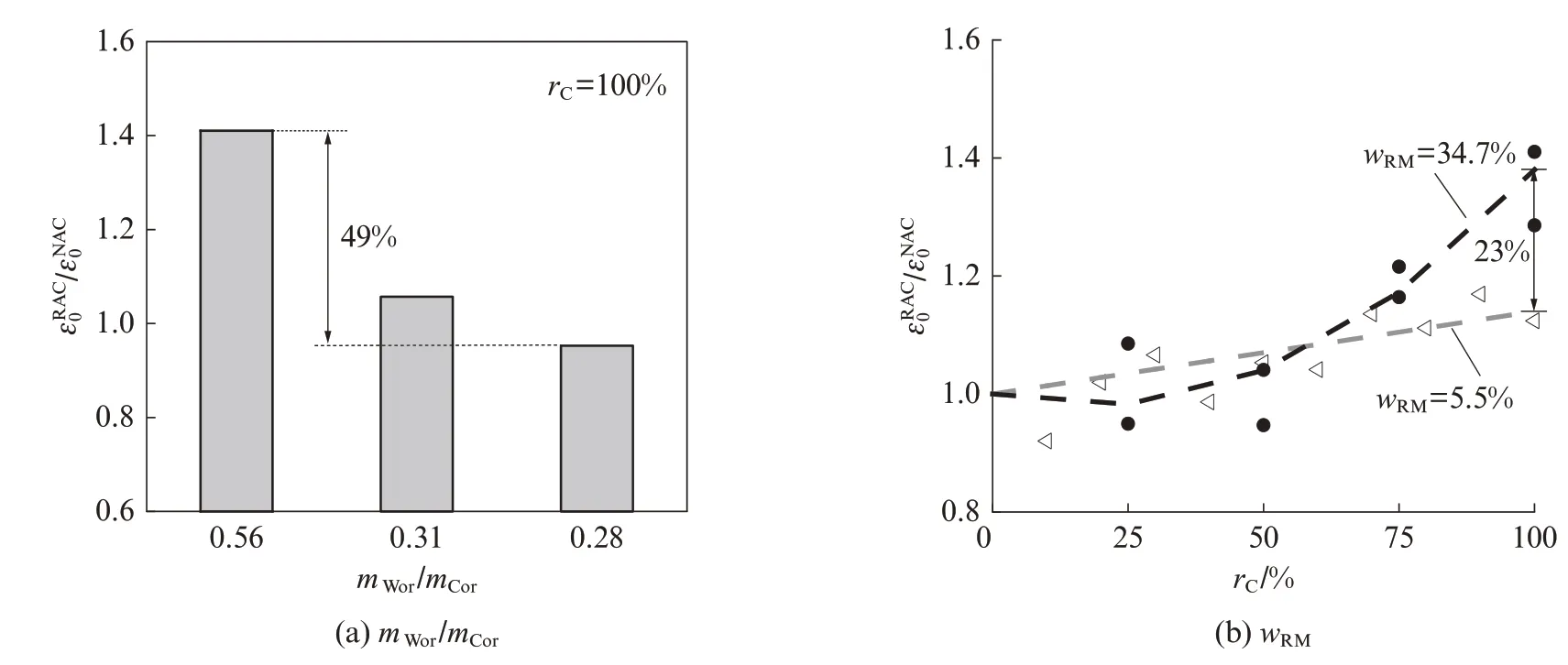
图3 不同基体混凝土水灰比及残余砂浆含量的典型峰值应变数据对比Fig.3 Comparison of strain at peak stress for salient RAC with different m/m and w［5，15，24］WorCorRM

综上，以rC为主要参数的传统建模方法无法准确描述由基体混凝土水灰比及残余砂浆含量变化引起的再生骨料影响差异，具有局限性.

2 基于复合材料理论的再生混凝土峰值应变模型

文献［9］基于 Zhou 等［26］提出的复合材料理论（Reuss 模型），将再生混凝土视为由天然粗骨料、再生细骨料、残余砂浆和新砂浆组成的体系，并且认为再生骨料中残余砂浆与原天然骨料变形之间的关系也满足复合材料理论，采用再生混凝土与同配比普通混凝土峰值应变之比（kε-X=εRAC0/εNAC0，表示在“X”模型中εRAC0/εNAC0的数学描述）量化再生骨料的影响，建立了再生混凝土峰值应变的数学描述，如式（1）所示.

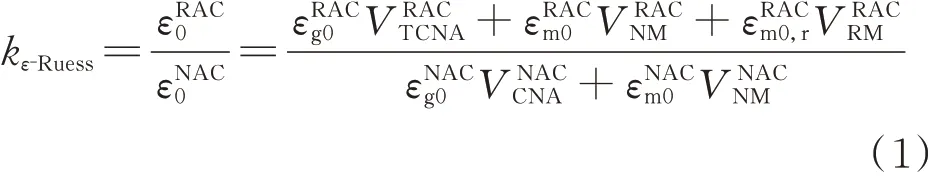
式中：εNAC0、εNACg0与εNACm0分别为当普通混凝土（NAC）轴向应力达到峰值应力fNACc时混凝土、天然骨料及砂浆的纵向应变；VNACCNA与VNACNM分别为普通混凝土中天然粗骨料与新砂浆的体积分数；εRAC0、εRACg0、εRACm0与εRACm0，r分别为当再生混凝土轴向应力达到峰值应力fRACc时混凝土、天然骨料、新砂浆与残余砂浆的纵向应变；VRACTCNA、VRACNM与VRACRM分别为再生混凝土中总天然粗骨料（包括新天然粗骨料及再生粗骨料中的原天然粗骨料）、新砂浆和残余砂浆的体积分数.

为对比所有常见复合材料模型［26］在预测再生混凝土峰值应变时的预测精度，本文沿用文献［9］模型的推导方法，建立了不同复合材料模型中εRAC0/εNAC0的数学描述，如式（2）～（4）所示.

根据文献［25］的建议，VRACTCNA、VRACNM与VRACRM可由式（5）～（7）计算.

在百雀羚产品线结构中，除了“天然不刺激”护肤绿之外，还有零售价4元的百雀羚凤凰甘油，以及个人护理系列花露水等非核心产品。同时男士系列也是刚性不足，削弱了百雀羚的品牌属性定位。引领百雀羚飞速发展的新生力量是草本系列，净化品牌旗下的产品也许是百雀羚下一步要做的工作。不可否认，基于现实销售规模等因素的影响，百雀羚目前仍没有淘汰与品牌属性定位不兼容的老品，未来产品线结构如何进一步优化提升，对于品牌操盘者是考验。

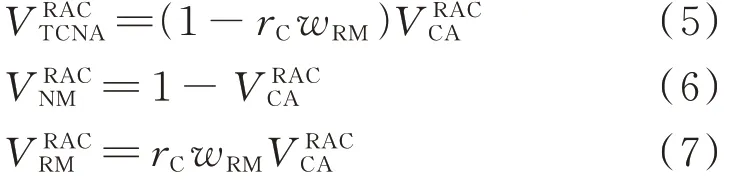
式中：Eg为骨料的弹性模量，MPa；ENACm，sec为当普通混凝土轴向应力达到峰值应力时新砂浆的割线模量，MPa；ERACm，sec、ERACrm，sec分别为当再生混凝土轴向应力达到峰值应力时新砂浆、残余砂浆的割线模量，MPa；VRACCA为再生混凝土中所有粗骨料的体积分数.

在混凝土加载过程中，骨料处于弹性阶段，因此骨料的变形（εRACg0与εNACg0）分别表示为：

式中：σRACg0、σNACg0分别为再生混凝土、普通混凝土达到峰值应力时骨料所承受的应力，MPa；对于 Ruess 模型（串联模型［26］）而言，二者为再生混凝土、普通混凝土的峰值应力；对于Counto模型而言，由于骨料、残余砂浆、新砂浆呈现并联 关 系［26］，因 此 σRACg0、σNACg0可 由 式（10）、（11）表示.

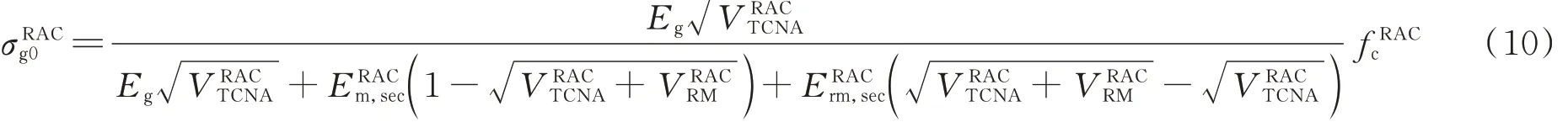
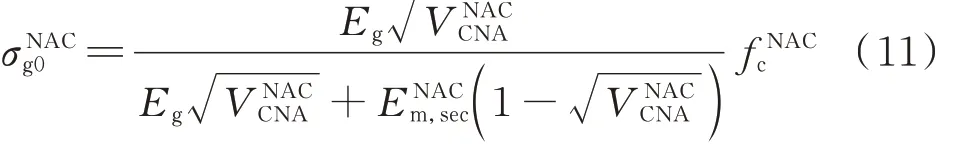
式（1）～（4）中砂浆的变形（εRACm0、εRACm0，r与 εNACm0）可以通过式（12）～（14）表示.

式中：σRACm0、σRACm0，r分别为再生混凝土达到峰值应力时新砂浆、残余砂浆所承受的应力，MPa；对于Ruess 模型而言，二者均为fRACc；对于Counto 模型而言，通过骨料、残余砂浆、新砂浆呈现的并联关系［26］可以得到σRACm0、σRACm0，r的计算公式，如式（15）、（16）所示；σNACm0为当普通混凝土达到峰值应力时新砂浆所承受的应力，可由式（17）表示.

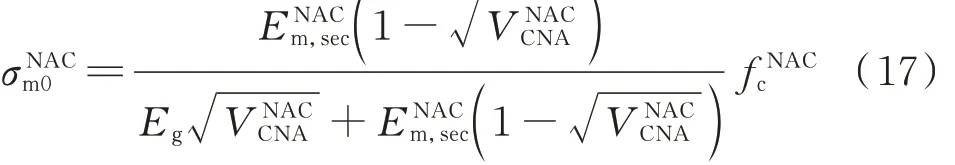
由上述模型的推导过程可知，再生混凝土、普通混凝土中砂浆的割线模量（即：ENACm，sec、ERACm，sec、ERACrm，sec）为关键计算参数，其取值应处于砂浆的弹性模量（Em、Erm）与 砂 浆 峰 值 应 力 所 对 应 的 割 线 模 量（Epeakm，sec、Epeakrm，sec）之间 . 根据 Kohee 等［27］的研究，砂浆峰值应力fm所对应的割线模量与其弹性模量之间存在如下关系：

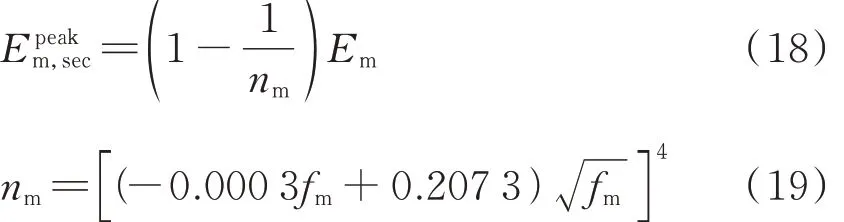
本文采用新旧砂浆弹性模量（Em、Erm）与其峰值应变对应割线模量（Epeakm，sec、Epeakrm，sec）的平均值为再生混凝土和普通混凝土中砂浆的割线模量（即，ENACm，sec、ERACm，sec、ERACrm，sec）代表值进行计算，如式（20）～（23）所示 .据试算，砂浆割线模量在砂浆的弹性模量及其峰值应变对应割线模量间变化时，在常用混凝土水灰比（0.30～0.60）以及常用残余砂浆含量（30.0%～50.0%）［2，17，28］范围内，对再生混凝土与普通混凝土峰值应变之比计算结果的影响不超过5%.

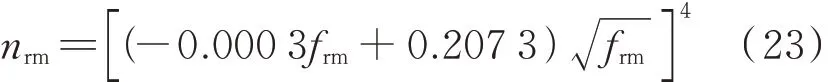
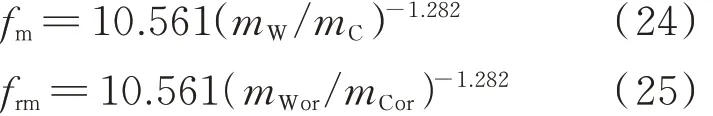
式中：mW/mC为再生混凝土的水灰比.

此外，基于文献［30］，天然骨料弹性模量的取值范围为69.0～88.7 GPa，砂浆弹性模量的取值范围为15～31 GPa，因此：

将式（8）～（27）代入式（1）～（4）中，可以推导得出不同复合材料模型中εRAC0/εNAC0值的计算表达式：

式中：

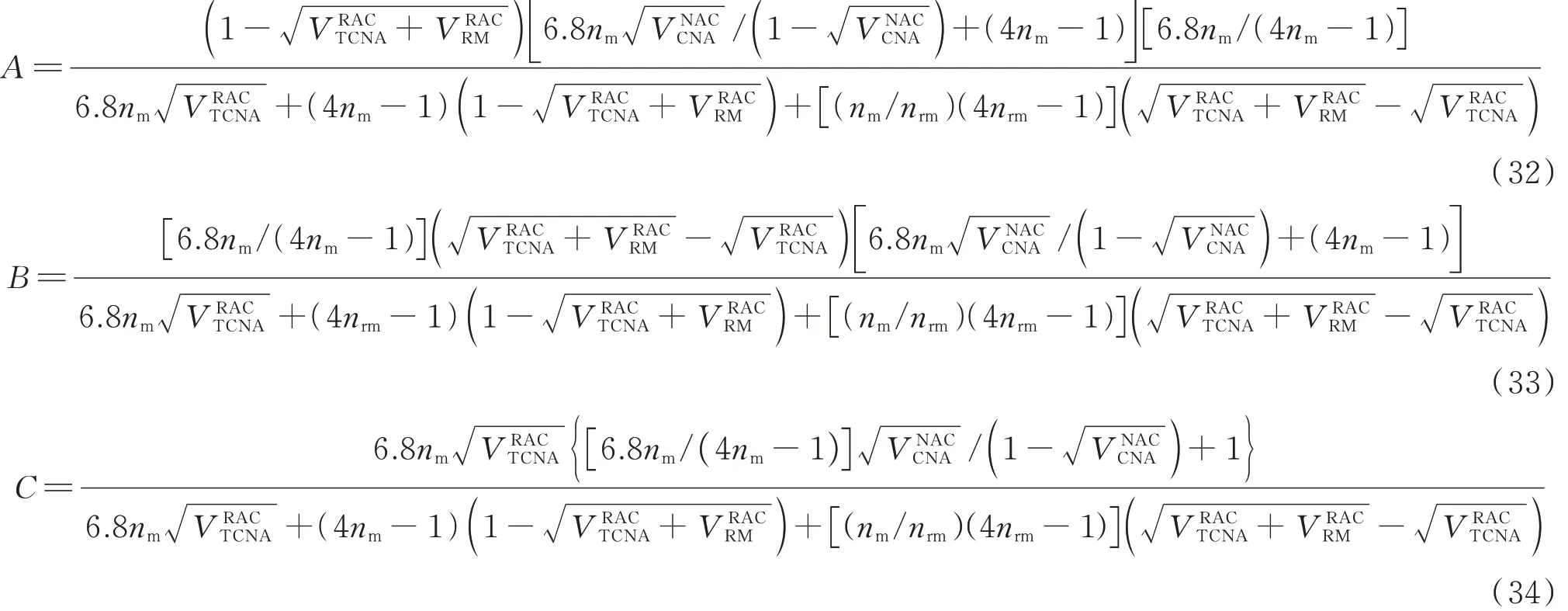
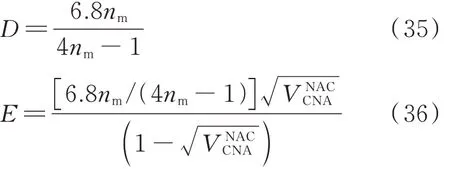
从式（28）～（36）可以看出，由不同复合材料模型推导的再生混凝土峰值应变计算模型差异较大，其中Voigt 模型和Ruess 模型较为简单，而Hirsch模型和Counto 模型较为复杂. 为评估各模型预测结果的可靠性，下文将对上述模型进行系统参数分析，并将现有试验结果与各模型的预测结果进行对比.

3 预测结果对比分析

3.1 参数分析

采用各再生混凝土峰值应变模型进行参数分析，结果如图4 所示. 其中，残余砂浆含量为20.0%～50.0%，基体混凝土水灰比为0.30～0.60，再生混凝土水灰比为0.45，再生粗骨料取代率为0%～100%，天然粗骨料与再生粗骨料的表观密度再生骨料对峰值应变的影响.

从图4 可以看出，随着再生粗骨料取代率、残余砂浆含量及基体混凝土水灰比的提高，再生骨料对峰值应变的影响逐渐增大，但增大幅度存在较大差异.例如，对于基体混凝土水灰比为0.30 且残余砂浆含量为20.0%的混凝土，100%取代天然粗骨料将使峰值应变预测结果增大4.4%～8.6%；当基体混凝土水灰比增至0.45 且残余砂浆含量为40.0%时，此预测结果将增大至15.2%～21.2%.

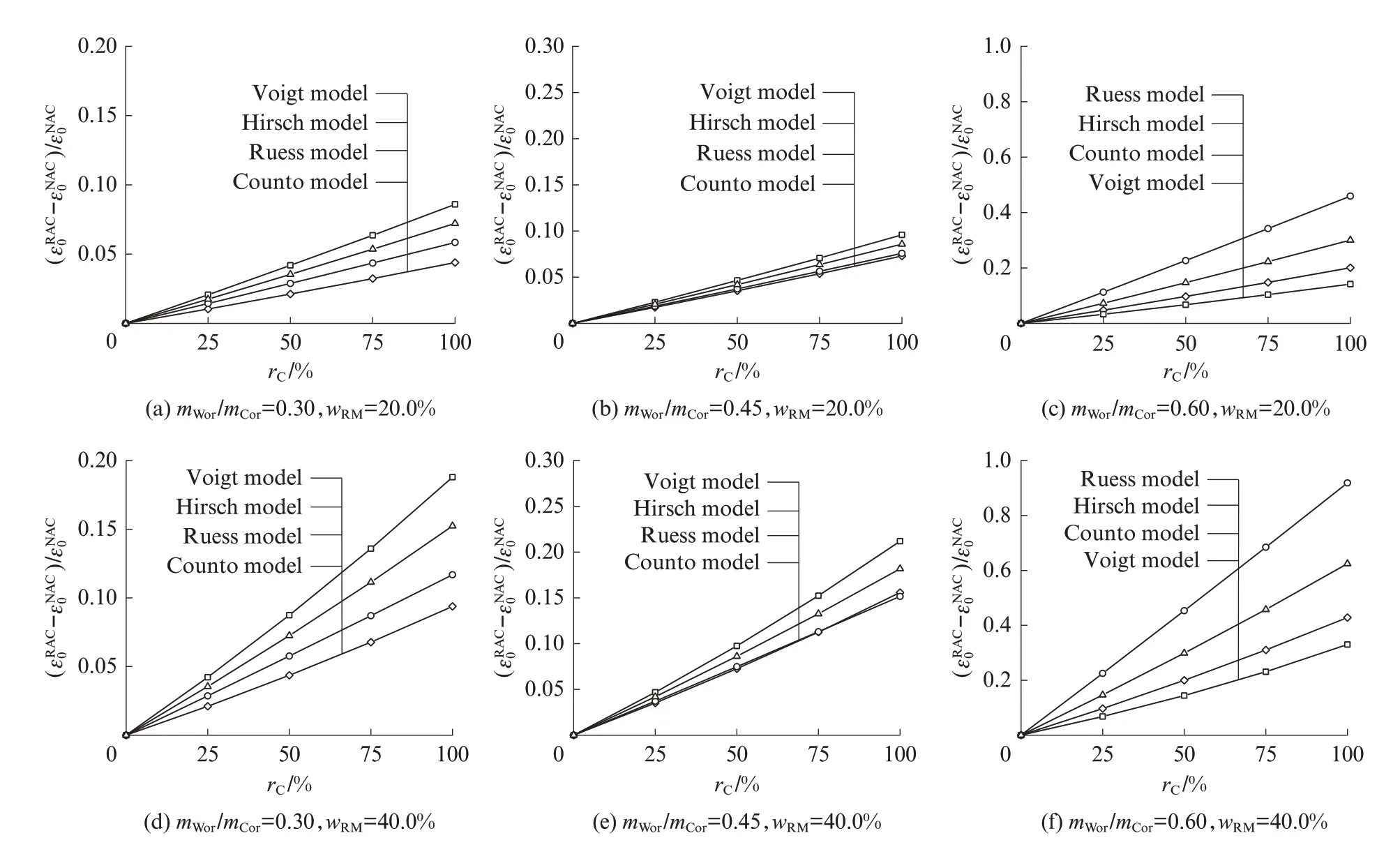
图4 各模型峰值应变的计算结果对比Fig.4 Comparison of predictions for each peak strain model

各模型预测结果的差异也随着再生粗骨料取代率、残余砂浆含量和基体混凝土水灰比的增大而显著增大. 例如，对于mWor/mCor=0.30 与wRM=20.0%的混凝土，当再生粗骨料取代率从25%增至100%时，各模型差异将由1.04%提高至4.2%（图5（a））.当采用100%再生粗骨料且基体混凝土水灰比为0.30 时，残余砂浆含量从20.0%增大至40.0%将使模型预测结果差异由4.2%提高至9.4%.当残余砂浆含量为20.0%且再生粗骨料取代率为100%时，基体混凝土水灰比由0.30 增至0.60，各模型最大差异将由4.2%增大至31.7%.

3.2 基于试验结果的模型对比

3.2.1 模型验证

将所提出的再生混凝土峰值应变预测模型与收集到的 100 组现有试验结果［5，7，9，15-17，19-24］进行对比，如图5 所示.所采用的试验数据基本涵盖了工程中常用的再生混凝土参数范围：再生粗、细骨料取代率为0%～100%、再生混凝土水灰比为0.25～0.65，基体混凝土水灰比为0.28～0.65，残余砂浆含量为5.5%～40.0%. 需要说明的是，根据前期研究的建议［31］，除文献［9，15，17，24］外，其余试验中的基体混凝土水灰比结果均基于JGJ 55—2011《普通混凝土配合比设计规程》中抗压强度与水灰比的关系表达式得到.由图5 可以看出，当基体混凝土水灰比比再生混凝土水灰比高时，Voigt 模型的预测结果偏低，而Ruess 模型会高估再生骨料对峰值应变的影响，二者差异可达63.2%. 此时预测结果与试验结果之比的 平 均 值 为 0.961～1.040，变 异 系 数（COV）为0.095～0.106.与前期对弹性变形的研究相似［25-26］，采用串、并联模型结合的Hirsch 模型与Counto 模型，其预测精度较高，离散性较低.预测结果与试验结果之比的平均值为0.978～1.000，变异系数为0.072～0.080.

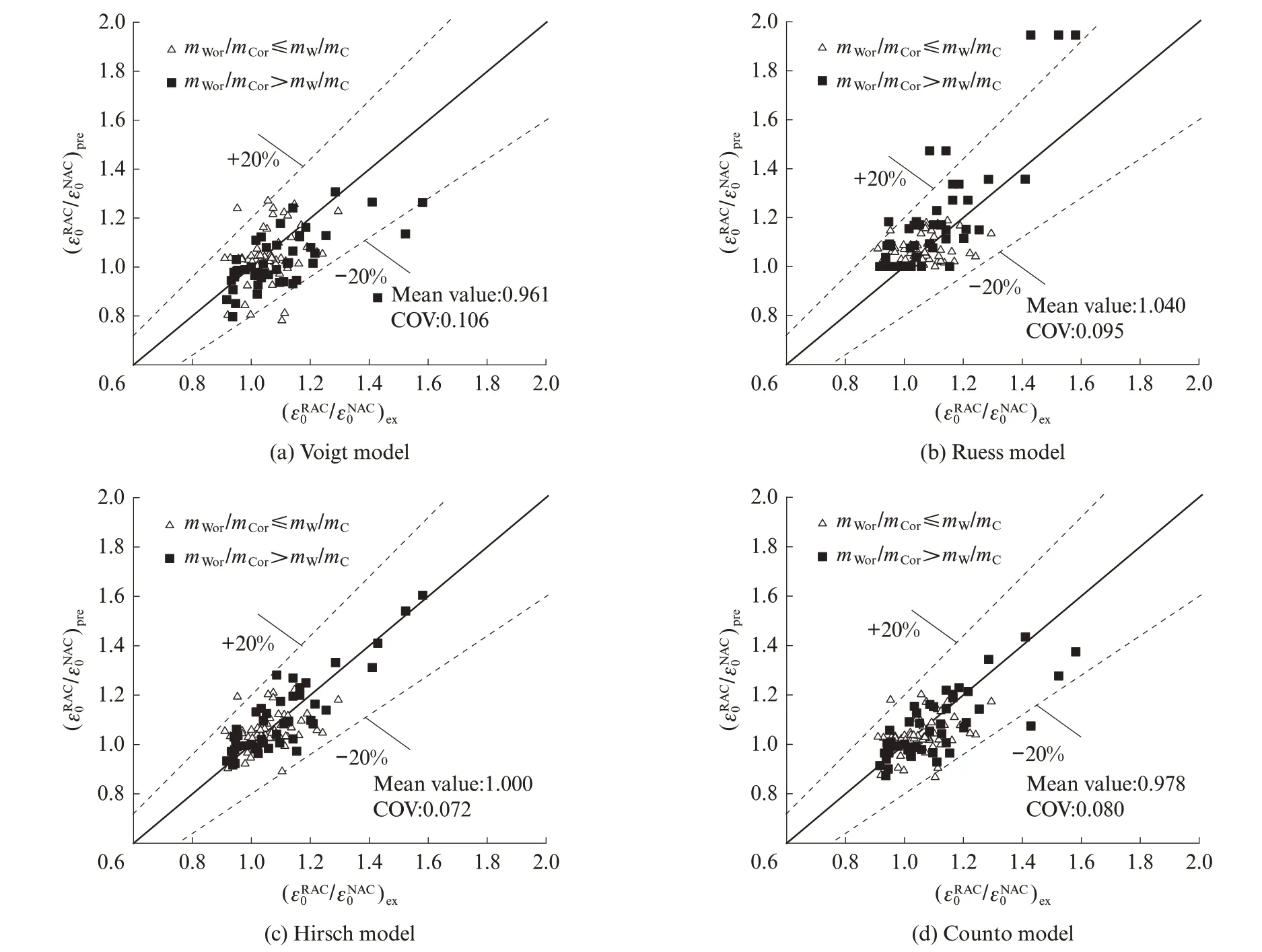
图5 各模型预测结果与试验对比Fig.5 Comparison of predictions and test results for each peak strain model

3.2.2 基体混凝土水灰比及残余砂浆含量对预测精度的影响

为说明考虑基体混凝土水灰比及残余砂浆含量影响的必要性，将本文模型（Hirsch 模型、Counto 模型）与不考虑上述影响因素的模型预测结果进行对比，如图6 所示.图中采用了基体混凝土水灰比较高与残余砂浆含量较低（mWor/mCor＞mW/mC及 wRM＜20.0%）的典型试验结果进行对比验证.由图6 可以看出，本文所提模型可较好地预测典型试件的测量结果，最大差异不超过10%.然而当不考虑基体混凝土水灰比及残余砂浆含量影响时，模型则无法准确混凝土峰值应变，最大差异达45%.考虑到Counto 模型的表达式形式较为复杂，本文推荐采用Hirsch 模型来预测再生混凝土的峰值应变.

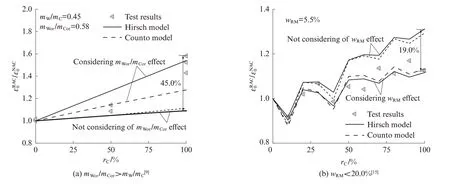
图6 不同基体混凝土水灰比及残余砂浆含量的典型试件预测峰值应变与试验结果对比Fig.6 Comparison of predicted peak strain and measured results for salient RAC with different mWor/mCor and wRM

4 结论

（1）基体混凝土水灰比mWor/mCor和残余砂浆含量wRM对再生混凝土峰值应变的影响显著.对于100%取代再生粗骨料的混凝土，当mWor/mCor由0.56下降至0.28 时，再生骨料的影响幅度下降49%；当wRM由5.5%提高至34.7%时，该影响幅度增大23%.

（2）基于复合材料理论，采用理论推导方式建立了4 种可考虑mWor/mCor以及wRM影响的再生混凝土峰值应变模型.各模型预测结果的差异随着再生粗骨料取代率、wRM与mWor/mCor的增大而显著增大，差异可达31.7%.

（3）Hirsch 模型和Counto 模型的预测精度较高，离散性较低.特别是在预测基体混凝土水灰比较高与残余砂浆含量较低（mWor/mCor＞mW/mC及 wRM＜20.0%）的混凝土时呈现明显优势，预测结果与试验结果之比的平均值为0.978～1.000，变异系数为0.072～0.080.考虑到Counto 模型较为复杂，本文推荐使用Hirsch 模型进行预测.