基于模态参数与改进萤火虫算法的结构模型修正
2022-12-04封周权王文赞华旭刚陈政清
封周权,王文赞,华旭刚,陈政清
[1.湖南大学土木工程学院,湖南长沙 410082;2.风工程与桥梁工程湖南省重点实验室(湖南大学),湖南长沙 410082]
在土木工程领域中,基于有限元技术的数值模拟方法广泛应用于结构静力分析、结构动力分析、结构或构件设计等各个方面[1],通过建立有限元模型可为结构行为预测提供重要参考.有限元模型修正实质上是一种系统识别问题,通过修正模型参数来尽可能缩小模型响应数据与实测响应数据之间的差别,从而使得有限元模型更加接近实际工程结构.模态参数(频率、振型等)是表征结构动力特性的主要参数,因此基于模态参数的模型修正得到了广泛的应用.求解使得模态参数模型预测值与实测值之间误差取得最小值时的模型参数,即得到了模型参数的最优值,因此模型修正在数学上实际是一个优化问题.针对优化问题的求解,现已有多种算法得到了应用,如模式搜索法[2]、拟牛顿法[3]、元启发式优化算法等.其中元启发式优化算法由于其优越的全局寻优能力和较好的准确性而受到了学者们的青睐.王家等[4]提出新的启发式算法来求解施工现场设施布局的优化问题;Feng 等[5]针对类电磁机制算法提出改进措施,并成功应用于三层剪切框架的结构损伤识别.
萤火虫算法(FA)作为元启发式优化算法的一种,具有控制参数少、物理意义简单明了的特点,具有良好的寻优性能[6],但同其他元启发式优化算法,如遗传算法(GA)、粒子群算法(PSO)等一样,存在容易陷入局部最优、早熟、不收敛的问题,因此学者针对原始萤火虫算法的不足提出了诸多改进措施[7-12].
本文基于模态参数识别技术,使用作者提出的改进萤火虫算法对二维桁架数值模型和六层剪切框架实验模型进行模型修正,并将其识别结果与原FA、GA、PSO 等算法识别结果进行对比,验证了改进优化算法的优越性.
1 目标函数
对于线弹性结构模型,频率和振型的预测值与其质量和刚度矩阵直接相关.假设结构的质量矩阵M已知,结构模型修正仅考虑刚度修正,且引入刚度修正系数θ来描述刚度变化程度.修正系数θ∈[-1,1]为一个1×N维向量,其中N为未知量个数,应为结构的单元个数.若θi>0,则表示第i个单元刚度提高,若θi<0,则表示该单元刚度降低.另假设结构在未受损伤状态下第i个单元的刚度矩阵为ki,那么修正状态(损伤状态)的刚度矩阵K(θ)可表示为:

结构的频率和振型预测值可以由其特征方程求解得到:

式中:ω为结构圆频率,与结构物理频率f有ω=2πf的关系;ϕ为与之对应的特征向量,即结构的振型.
在结构动力实测中,受制于人力、成本、器材等诸多因素,高阶模态参数往往难以精确获取,全自由度测量也经常难以实现,因此假设实测仅可获得前m阶模态和nd个自由度,并重复测量ns次,即可获得ns组m阶频率和不完整振型实测值.将模态参数实测值与预测值之间的误差分别按频率和振型以及模型阶数进行累积,设计目标函数[5]:
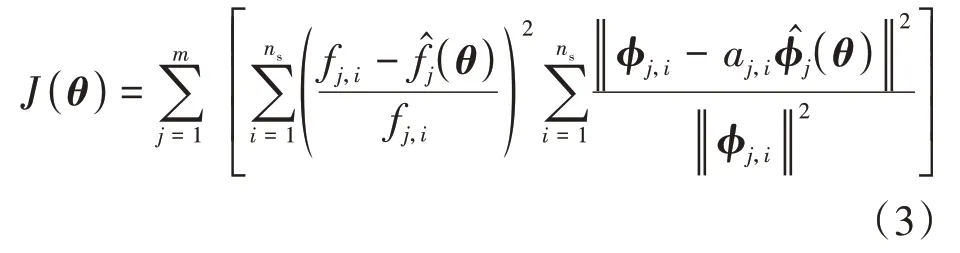
式中:aj,i=为比例系数,确保预测模态振型在测量自由度处与实测模态振型最接近;分别为结构第j阶模态频率和振型向量预测值,它们是将式(1)代入式(2)并通过模态分析计算得到的;fj,i和ϕj,i分别为第j阶模态频率和振型向量的第i次实测值,它们是通过实验模态参数识别得到的.为避免振型和频率误差水平的不同,公式(3)以实测值(振型向量取实测值的模)为分母进行了归一化处理.
2 原始算法与优化算法
2.1 萤火虫算法
萤火虫算法最早由Yang[13]提出,是一种以自然界中萤火虫发光行为[14]为启发的全局优化算法.萤火虫算法通过建立不同萤火虫个体之间相互吸引机制,从而达到在空间内寻找最优解的目的,即若某萤火虫荧光亮度(I)越亮,则对其他个体的吸引力(β)也就越强.
萤火虫算法做了以下3点假设:
1)萤火虫没有性别上的区分,即所有萤火虫之间的相互吸引不受性别的影响.
2)萤火虫的吸引力(β)与荧光亮度(I)成正比,且两者都随距离的增加而降低.
3)萤火虫的亮度(I)取决于该萤火虫个体所处目标函数中的位置.
在一定的导光介质中,光线强度以高斯分布的形式随距离的增加而衰减:

式中:r为两相邻萤火虫之间的空间距离;I0为距离r=0时的荧光亮度;γ为导光介质的吸收系数,其值的大小代表了介质对光亮衰减的影响程度.
萤火虫的吸引系数同样以指数的形式随距离的增加而衰减:

式中:β0为吸引系数初值,代表两萤火虫之间距离r=0时的吸引系数.
两萤火虫之间的距离满足笛卡儿坐标系下的空间距离计算方法:
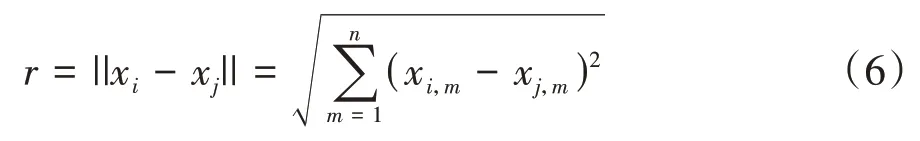
式中:n为优化问题的自变量总数,即解的总维数;xi,m是第i只萤火虫第m维变量.
如前所述,荧光亮度(I)较亮的萤火虫可吸引较暗的萤火虫向其移动,假设第i只萤火虫荧光亮度较第j只萤火虫弱,则萤火虫i的移动方式和移动量受式(7)约束:
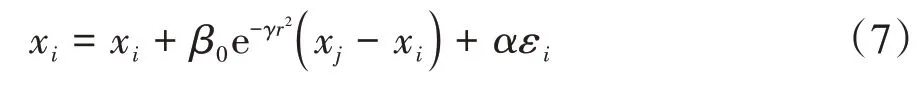
2.2 改进萤火虫算法
改进萤火虫算法(modified Nelder-Mead Firefly Algorithm,m-NMFA)在原标准FA 算法的基础上提出4 点改进措施,包括引入下山单纯形局部优化算法(Nelder-Mead Algorithm),并针对算法的结构、参数以及局部搜索提出了改进措施,如引入多样性阈值、引入边界控制因子、对参数进行修改等.
2.2.1 参数修改
大量的研究证明,改变步长α和吸引系数β对萤火虫算法的求解精度、收敛速度等都有较大的影响[6-7,11,20-23].
经过测试发现,在迭代过程的前期,步长偏小的往往会收敛更快,这个规律适合不同的步长公式和测试函数,但如果步长减小过快,在后期容易陷入局部最优解而难以寻找到全局最优解,使算法早熟.因此,步长在迭代后期逐渐趋于0 的过程中仍应保持足够大的值,以最大限度地保持探索与开发之间的平衡[24-25].据此设计出较为理想的步长公式:
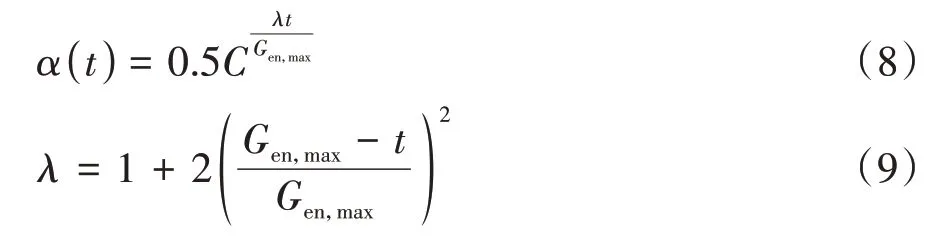
式中:α(t)表示第t迭代步的随机移动的步长;C=1.0×10-10;Gen,max表示最大迭代次数;λ∈[1,3]为参考系数,其值随着迭代次数t的增加呈非线性递减趋势.引入参考系数λ可实现对步长大小变化趋势的控制.
为使步长大小与可行域大小相适配[25],在式(7)αϵi项中引入缩放参数(scaling parameters)Sk.

式中:lk和uk分别为某萤火虫个体的第k个未知量所对应的下界和上界.如此,式(7)可写为:
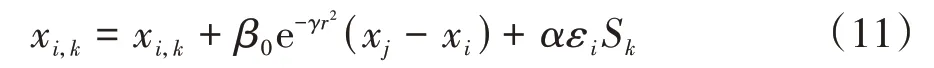
对于吸引系数,引用Selvarasu[23]在其改进方法中给出的吸引系数计算公式,以保证算法的精确度和收敛速度:

式中:βmin=0.2 为吸引系数β的下界,βmax=1 为吸引系数β的上界,因此有β∈[βmin,βmax].
2.2.2 边界约束处理机制
萤火虫算法与其他元启发式优化算法类似,个体有可能出现在所定义的边界之外[26],这些个体将对算法的精度和收敛速度均产生不利影响,甚至得到完全错误的结果.使用有效的边界约束处理机制可以很好地避免此类问题的发生,并提高搜索算法的优化性能[27-28].
在已有的边界约束方式中,较多的学者[15,22,27-28]针对萤火虫个体中溢出的某个未知量而非单个个体进行处理,但多维度问题的最优解是由各个未知量共同决定的,因此提出新的边界约束处理机制,即当某萤火虫个体的某未知量超出边界值时,首先在可行域范围内随机生成新的萤火虫个体,然后将该萤火虫个体向当前最优解移动一定距离,在移动时能够保证移动幅度不超过该萤火虫与当前最优解之间距离的1/2,以最大限度地保证个体多样性.其伪代码如下:
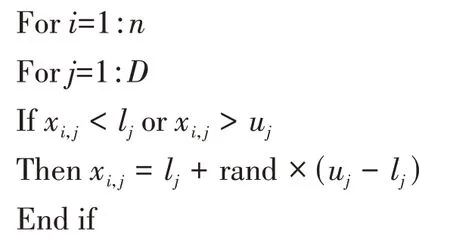
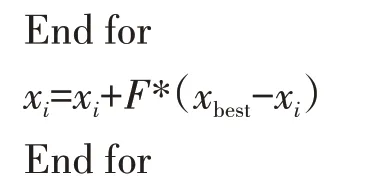
其中,rand 为0~1 的随机数,F∈[0,0.5]为随机因子,xbest为当前全局最优解.
2.2.3 下山单纯形算法及多样性阈值
下山单纯形算法是一种局部优化算法,与群体智能优化算法通过一定规模个体随机寻求最优解的方法不同,它在给定的初始解附近生成N+1 个顶点的凸多面体,在此基础上通过反射、扩张、收缩和压缩等运算逐渐逼近精确解[29].因此在萤火虫算法迭代过程中及运行结束后,使用下山单纯形算法在最优解附近挖掘更优解,以提高算法求解能力.
在迭代过程中,启用单纯形算法的时机将直接影响求解的精度和收敛速度,若启用过早,则接近真实解的最优解还未找到,单纯形算法频繁调用,将降低求解效率;若启用过晚,通过单纯形算法挖掘到的更优解对算法整体的贡献将会被削弱,因此引入多样性阈值概念以解决上述矛盾.记xk,best和xk,worst分别为第k次迭代最优解和最差解,xg,best和xg,worst分别为当前全局最优解和最差解.多样性阈值计算公式如下:

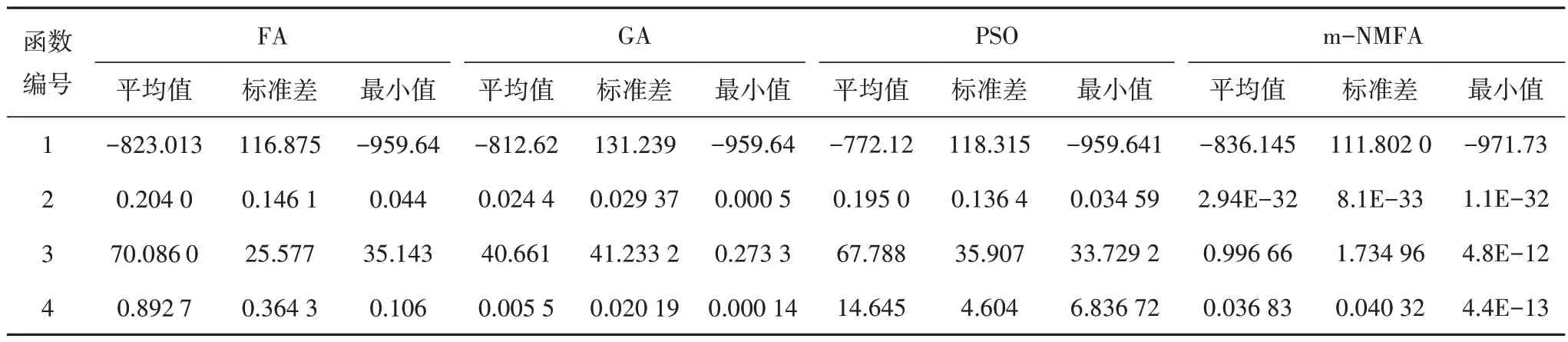
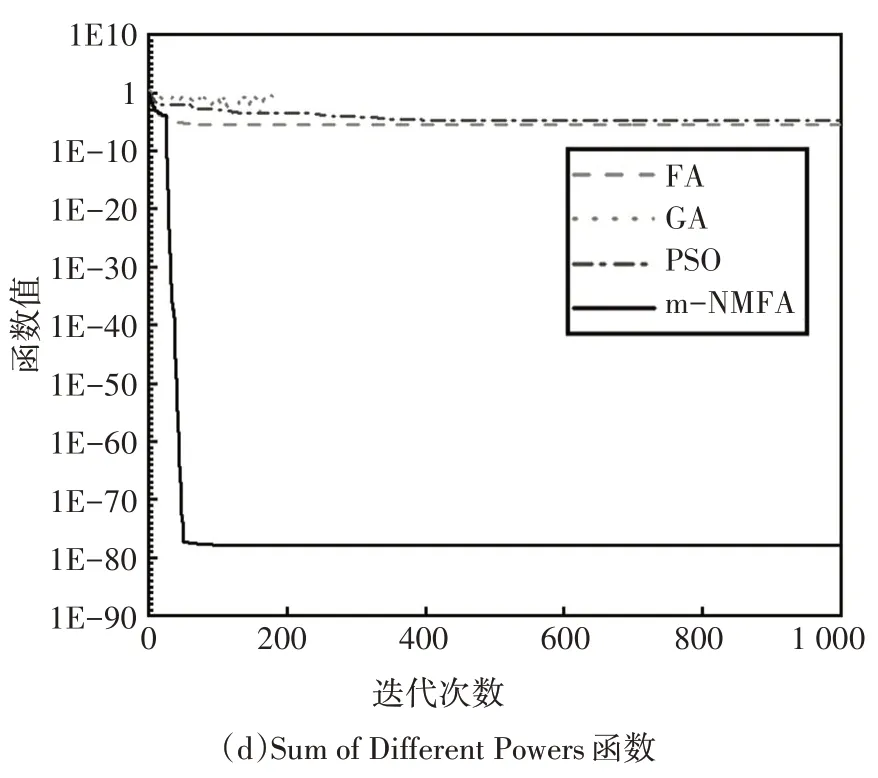
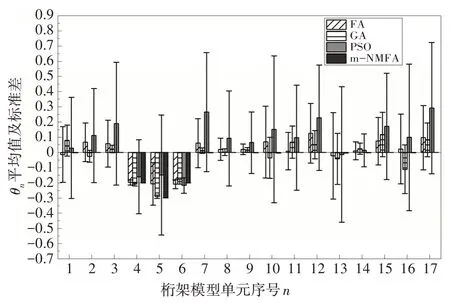
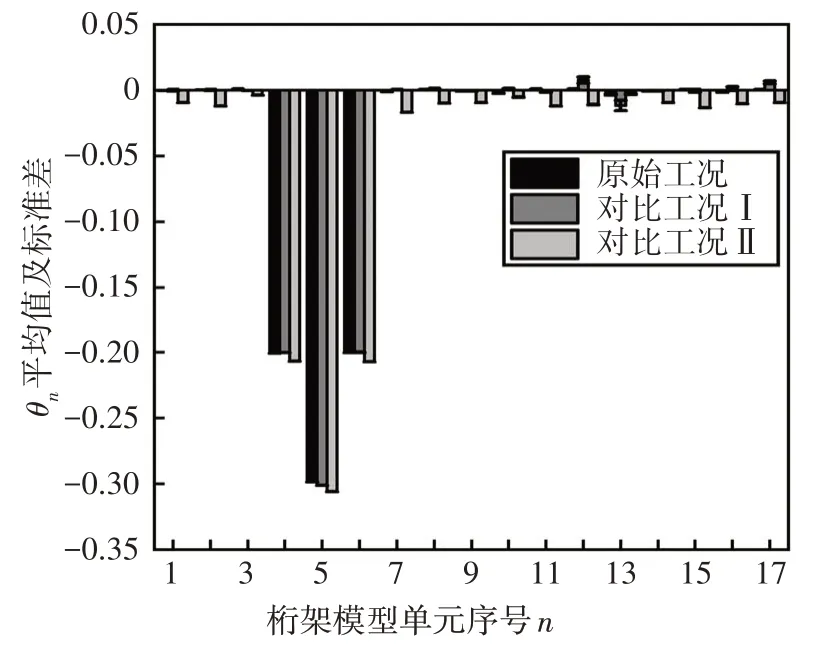
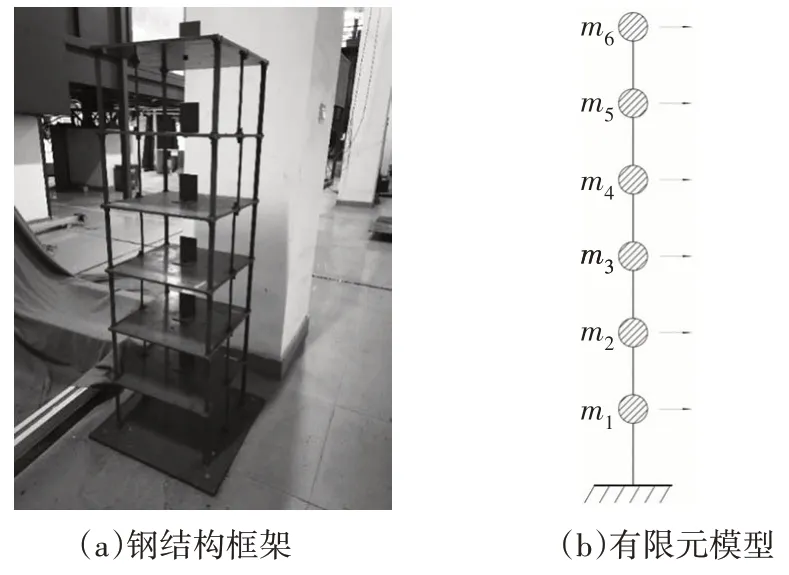
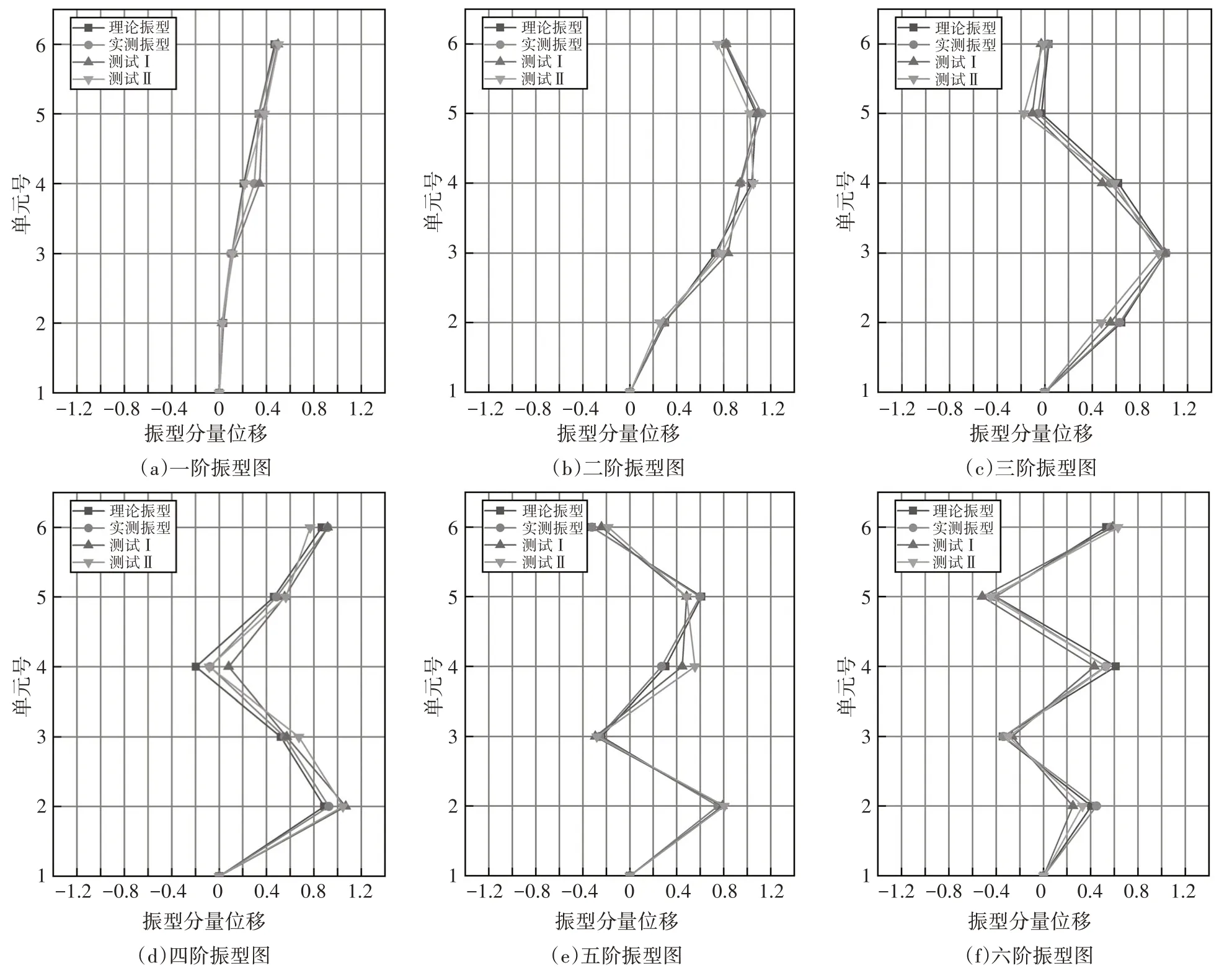
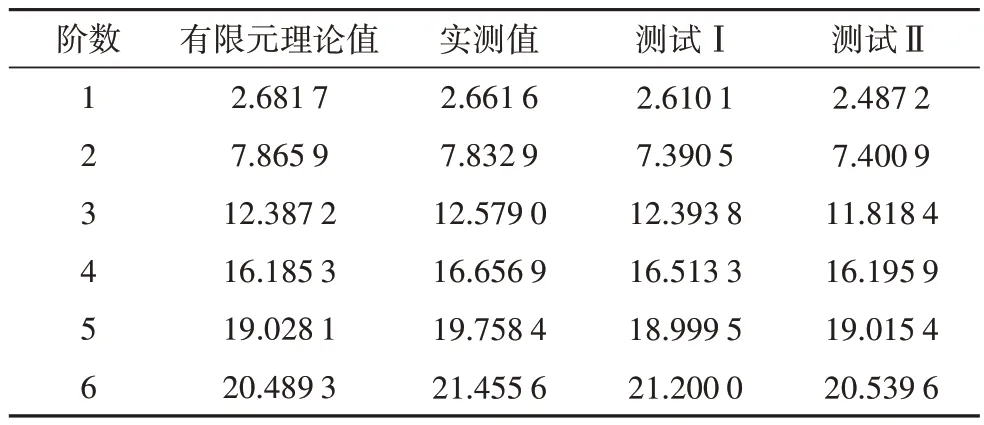
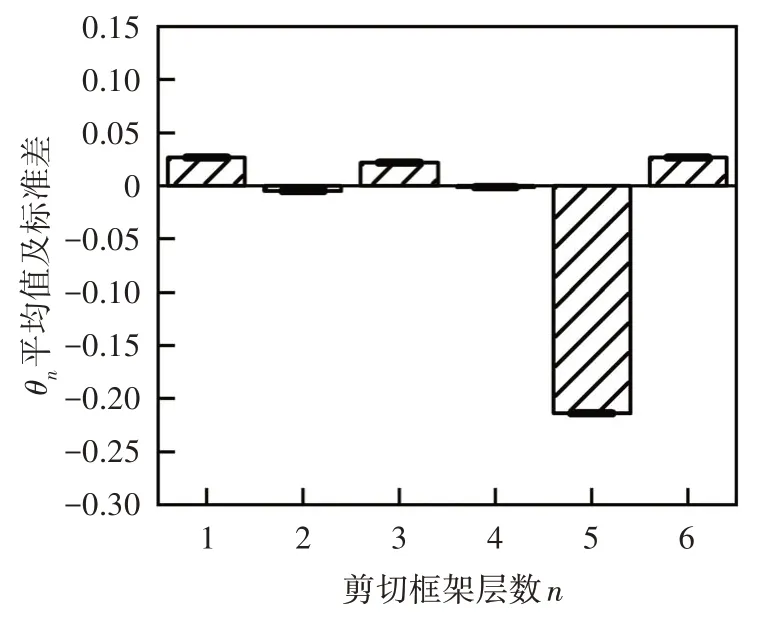
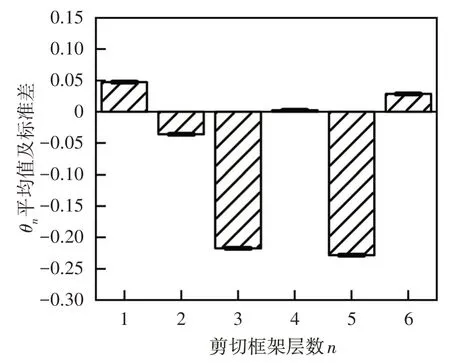
规定当eξ-1 经过测试,取M=0.001 是相对合适的,此时算法已经能够找到接近于真实解的全局最优解,而且经过若干次的迭代,步长α已经足够小,能够与单纯形算法相适配. 为了验证改进优化的求解效果,选用表1 所示的4 个基准测试函数将FA、GA 和PSO 优化算法与m-NMFA进行对比,以验证改进算法的优越性.测试中,种群规模或染色体个数n均为30,最大迭代次数均为Gen,max=1 000.其中,m-NMFA 的步长初值为0.5,原始FA 采用Yang[15]对于多维度问题所采用的步长公式,步长初值为0.25.吸引系数βmin和βmax分别取0.2和1.0,光线吸收常数γ=1.0.对于GA,测试调用了Matlab 内置GA 优化算法,除染色体个数及最大迭代次数外,其他参数均采用Matlab 内置工具箱默认值.对于PSO,学习因子取c1=c2=2,粒子最大速度为1,惯性因子采用线性变化方程: 表1 基准函数Tab.1 Benchmark function 式中:ωi为第i次迭代的惯性因子,ω1取0.4,ω2取0.9.当某粒子某一维度的速度或位置达到或超出边界时,该粒子全部维度的速度或位置将会全被重置为边界值. 为对比各优化算法的稳定性,每个测试函数单独运算100 次,得到优化结果的平均值、标准差及最小值如表2所示. 从表2可以看出,m-NMFA 除了在函数4中的平均值和标准差略差于GA 外,其余计算结果均优于其他优化算法,尤其是在函数2 和函数3 中的平均值、函数2~4 中最小值、函数2 中的标准差精度较其他算法均大幅提高.由此看出,m-NMFA 可以使求解的精度大大提高,并且有足够的稳定性.图1为4 种优化算法收敛情况的对比结果,从图1 可以看出,m-NMFA 算法在收敛速度和运算精度上均明显优于其他3 种算法,并且存在第二、第三次深度求解的能力. 表2 优化算法解的平均值、标准差和最小值Tab.2 The mean,standard deviation and minimum of the solutions of the four optimization algorithms 图1 4种优化算法的收敛图Fig.1 Convergence diagrams of four optimization algorithms 数值模拟使用如图2 所示的两端简支桁架模型进行测试.图2 中桁架长10 m,材料弹性模量为6.88×1010Pa,密度为2 780 kg/m3,杆的横截面积为0.002 5 m2.数值模拟初始工况有如下假设:①测试值仅为前6阶模态以及图中箭头所指的9个自由度;②受环境影响,频率和振型的测试结果中均存在1%的白噪声;③结构的损伤仅考虑刚度损伤,第4、5、6 号单元分别受到了20%、30%和20%的刚度折减. 图2 简支桁架结构模型(单位:m)Fig.2 Schematic of the 17-bar planar truss(unit:m) 本次模拟同样采用FA、GA、PSO、m-NMFA 这4种优化算法做对比,除自变量个数做了调整外,其余参数均与基准函数测试保持一致.每种算法各测试100 次,得到各单元损伤系数θn的平均值和标准差,结果如图3 所示.此外,模拟试验采用两种对比工况与原工况作对比,以验证改进优化算法计算模型修正问题结果的准确性与稳定性.对比工况Ⅰ:在初始工况假设的基础上,将可测得的模态数从6 阶减少为4 阶;对比工况Ⅱ:在初始工况假设的基础上,将白噪声由1%增加为5%. 图3 原工况下不同算法计算得到的桁架模型损伤系数θn的平均值及标准差Fig.3 The mean and standard deviation of damage coefficient of the truss model of the original condition run by different algorithms 从图3 可以看出,FA、GA、PSO 三种优化算法的最优解与目标值存在较大偏差,离散程度较大.通过改进算法得到的受损处单元损伤系数平均值分别为20.05%、29.86%和20.03%,非受损处单元损伤系数误差均小于5%,与假设情况符合良好;最优解的标准差均小于10-3,离散程度低.因此可以认为,使用m-NMFA算法寻找模态参数识别问题的最优解是可靠的. 从图4 可以看出,对于工况Ⅰ,模态阶数减少至4阶后,改进算法仍能在损伤部位找到较准确的损伤系数,且第5号单元损伤系数较原工况的损伤系数偏差仅有0.22%;工况Ⅱ中受损处单元损伤系数相较于原工况分别存在3.33%、1.83%和3.57%的增加,对于土木工程结构而言,这将是偏保守和偏安全的结果. 图4 不同工况下m-NMFA计算得到的桁架模型损伤系数θn的平均值及标准差Fig.4 The mean and standard deviation of damage coefficient of the truss model of different working conditions run by m-NMFA 选用6 层钢结构剪切框架,通过测试模态参数并采用本文提出的改进萤火虫算法对模型刚度矩阵进行修正从而实现损伤识别.钢结构框架如图5(a)所示,结构由地脚螺栓固定在地面上,层间板长、宽、厚分别为450 mm、450 mm、10 mm,各板在厚度中点处距离均为250 mm,各个层间板之间的刚度由分布在层间板4 个顶点处的主要柱和侧边中点处的附加柱提供.剪切框架的有限元模型采用如图5(b)所示的6 自由度集中质量模型.各层间板中心位置处设置一块竖直挡板,并使用采样频率为200 Hz 的IL-300 激光位移计来测量挡板底部的位移.试验测试了5 层附加柱缺失(测试Ⅰ)、第三和第五层附加柱缺失(测试Ⅱ)两种工况,为保证测试结果的准确性与稳定性,每种工况均重复测量50 次,每次持续时长5 min.剪切框架前6 阶固有频率和振型如表3 和图6 所示,其中表3 所列频率为50 次测量的平均值,振型均为位移归一化后的结果. 图5 钢结构剪切框架及其集中质量有限元模型Fig.5 Steel structure shear frame and its lumped mass finite element model 图6 剪切框架试验前6阶振型图Fig.6 The first 6 mode shapes of the shear frame tests 表3 剪切框架试验前6阶频率Tab.3 The first 6 natural frequencies of the shear frame tests Hz 试验测得的结果如图7和图8所示.在测试Ⅰ中,第五层刚度减少21.36%;在测试Ⅱ中,第三层和第五层结构刚度分别减少21.76%和22.81%.两组测试中,未损伤层的结构刚度平均值误差均在5%以内,因此可以认为,改进的优化算法能够准确识别结构损伤的位置,并且能够得到符合实际期望的最优解. 图7 测试Ⅰ结构损伤系数平均值及标准差Fig.7 Mean and standard deviation of structural damage coefficient of test Ⅰ 图8 测试Ⅱ结构损伤系数平均值及标准差Fig.8 Mean and standard deviation of structural damage coefficient of test Ⅱ 基于结构的模态参数数据,通过m-NMFA 改进萤火虫算法寻找模型参数最优解,成功地识别出受损结构的刚度变化,主要结论如下: 1)改进萤火虫算法可在保持较强全局搜索能力的同时,引入4点改进措施,极大地提高了局部搜索能力,其最优解相比于其他优化算法更精确、更稳定. 2)基于结构的频率、振型等模态参数,采用改进算法可利用较少的模态阶数和自由度,在一定白噪声影响下准确地找到结构损伤的位置,并求得有较高可信度的刚度损伤,为有限元模型修正准确度提供了有力保证,具有很好的实用价值.3 数值方法测试
3.1 基准函数测试

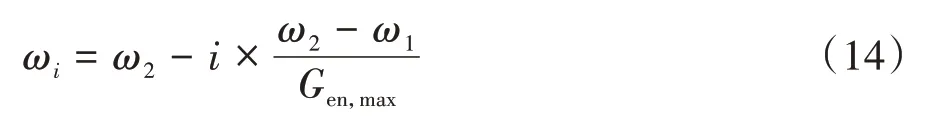

3.2 桁架模型数值模拟

4 剪切框架试验
5 结论
