软土地基基坑开挖对临近桩变形影响的时效分析

江杰，张探，欧孝夺†，柴文成，龙逸航

［1.广西大学土木建筑工程学院，广西南宁，530004；2.工程防灾与结构安全教育部重点实验室（广西大学），广西南宁，530004；3.广西防灾减灾与工程安全重点实验室（广西大学），广西南宁，530004］

随着经济的快速发展和城市人口的迅速增加，建筑物密度日益增大，越来越多的软土基坑在既有建筑结构附近进行开挖，基坑开挖会引起邻近桩基的附加应力和附加变形，进而对建筑结构产生不良影响，甚至造成工程事故的发生.针对基坑开挖对邻近桩水平位移的影响，国内外学者已进行了诸多研究［1-7］.

但上述研究主要关注的是瞬时开挖工况下邻近桩基水平位移变形，开挖完成后桩的长期连续变形可能发展到超过允许值，对邻近桩基造成破坏，特别是在软黏土地区［8-10］.因此，有必要发展软土地基基坑开挖卸荷后临近桩基长期连续变形计算和预测的理论方法.软土地基的长期连续变形与土体的蠕变性密切相关.目前有关考虑软土蠕变对桩基影响的研究［11-14］中多将蠕变模型取作整数阶导数黏弹性模型，由于整数阶微分算子的限制，不可避免地对应力或应变随时间变化的路径造成了限制.Zhu 等［15］发现，整数阶导数黏弹性模型在预测土体蠕变变形一段时间后与实验数据出现偏差，几乎无法拟合实验数据，为了准确地描述实验数据，往往要剔除高阶微分项或缩小本构关系的适用范围；Gemant［16］提出利用分数阶导数来模拟材料的蠕变性能，随后一些学者［17-19］对分数阶黏弹性模型在实际工程中的应用进行研究，发现分数阶黏弹性模型相比于经典黏弹性模型，能够更精确地刻画土体蠕变变形的力学行为，且仅需少数几个实验参数即能在较宽的范围内预测土体变形随时间的变化趋势.

同时，有关既有桩基在邻近基坑开挖下的响应理论解析中大多将桩基看作放置在Winkler 地基上的Euler-Bernoulli 梁.在实际工况下土体表面某点的变形值与该点所受的压力值不成正比，在外荷载作用下，土体弹簧相互之间存在剪切作用，Winkler地基模型不能考虑土体之间的剪切作用［20］，Paster⁃nak 地基模型通过在土体弹簧上加上一层不能压缩的剪切层来考虑土体相互之间的剪切效应.Euler-Bernoulli 梁基于平截面假定，没有考虑桩基剪切变形的影响，对于长径比较小的浅层桩基进行理论分析时会造成一定的误差［21］.相比于Euler-Bernoulli梁模型，Timoshenko 梁能够考虑桩基的弯曲和剪切效应.

针对上述不足，本文采用两阶段分析方法，第一阶段采用三维分数阶Merchant 黏弹性模型来描述土体的流变特性，解得弹性模量和泊松比在Laplace 域内的表达式，将表达式代入Mindlin 解中并通过La⁃place 变换方法解得邻近桩基附加应力的时域解；第二阶段将桩基看作放置在Pasternak双参数地基上的Timoshenko 梁，将所得附加应力作用在桩基上，建立桩身控制方程，采用有限差分法对附加荷载作用下桩基响应进行分析，得到基坑开挖引起临近桩水平位移的时域解.最后对Merchant 分数阶黏弹性模型参数进行分析.

1 分数阶黏弹性模型建立

分数阶导数微积分和整数阶微积分相比，微分和积分的阶为分数.在Lebesgue 积分区间（0，x）中，Riemann-Liourville定义下的分数阶导数为：

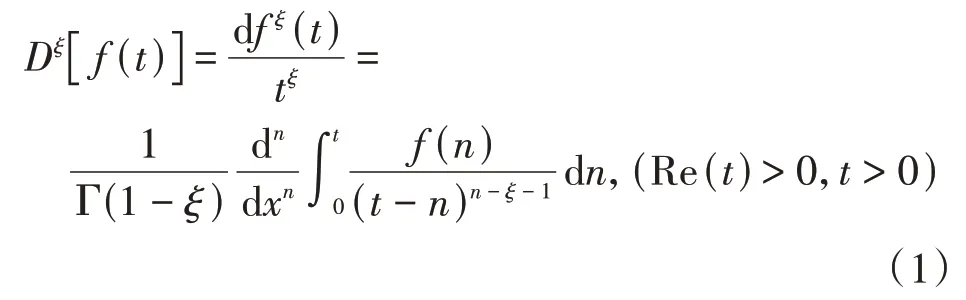
式中：f（t）为求导函数；ξ为分数阶且满足n-1≤ξ≤n；Γ(·)为Gamma函数.

为对桩身水平位移的时效性进行分析，需要对函数进行Laplace变换，整数阶函数表达式为：

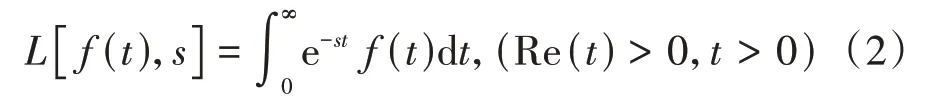
式中：s为复参变量；t为时间.假设f（x）在x=0的临边是可积的，则分数阶导数函数f（x）的Laplace 变换可写为：

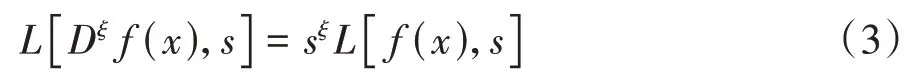
本文采用分数阶Merchant 黏弹性模型表示土的变形特性.分数阶Merchant 黏弹性模型由一个Hooke 弹簧元件与一个Abel 阻尼元件并联（即经典Kelvin 体），然后整体与另一个Hooke 弹簧元件（即Hooke 体）串联组成，其本构模型如图1 所示，图1 中α为分数阶，η为黏滞系数，G1为Hooke 体剪切模量，G2为Kelvin体剪切模量.

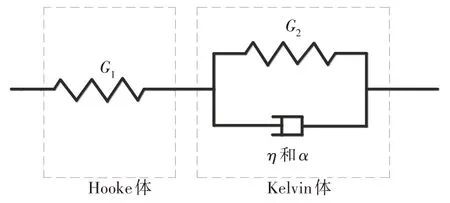
图1 一维分数阶Merchant黏弹性模型Fig.1 One-dimensional fractional Merchant viscoelastic model

文献［22］将一维三参量黏弹性模型推广至三维，并利用对应性原理得到了Laplace 变换域内的弹性模型和泊松比表达式，同理可得到三维分数阶Merchant 黏弹性模型的弹性模量和泊松比μ的Laplace表达式：

式中：λ=G1-αη，G为材料的剪切模量；s为复参变量；K为体积模量.

2 开挖引起的邻近桩基附加应力

2.1 软土地基中Mindlin时域解

在半无限弹性体任一点(x1，y1，z1)处作用沿z轴方向的竖向集中应力P0时，由Mindlin 应力解［23］可知，引起半无限弹性体任一点(x，y，z)处沿x轴方向水平附加应力为：

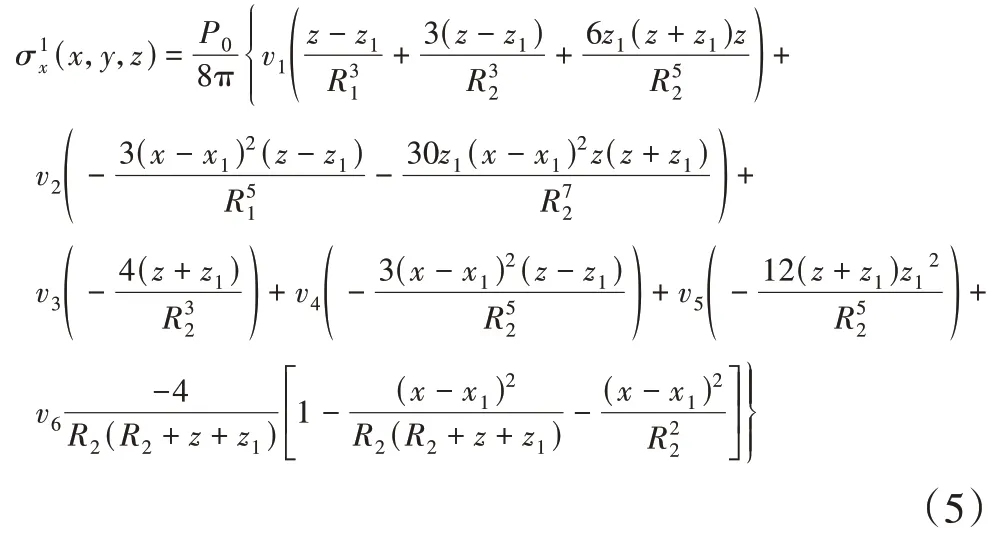
式中：v1=(1-2μ)/(1-μ)；v2=1/(1-μ)；v3=(1-2μ)μ/(1-μ)；v4=(3-4μ)/(1-μ)；v5=μ/(1-μ)；v6=1-2μ，其中μ为泊松比.

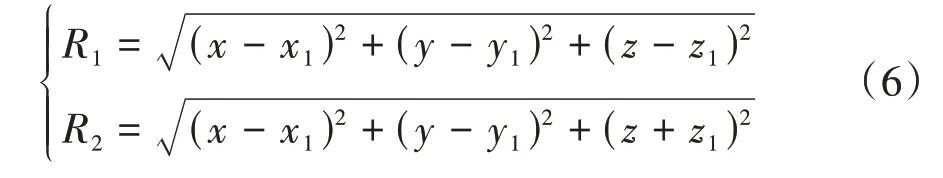
式中：A1～A6为公式（5）中v1～v6中的泊松比μ被公式（4）中替换所得.

对分数阶导数进行Laplace 逆变换时，分数阶导数有以下性质：

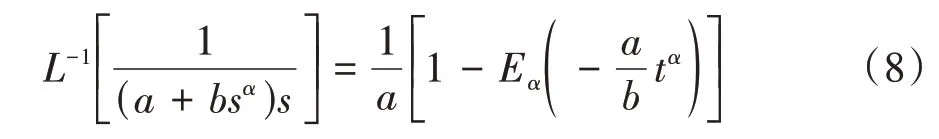
式中：a、b为任意代数式；Eα为含一个参数的Mittag-Leffler方程，其定义为：

半无限黏弹性地基承受集中荷载的作用，有P(t)=P0H(t)，其中H(t)为Heaviside，对其进行La⁃place变换可得：

将公式（10）代入公式（7）中并利用公式（8）定义的分数阶Laplace 逆变换公式进行变换可得基坑卸荷引起临近桩x方向的附加应力时域解为：

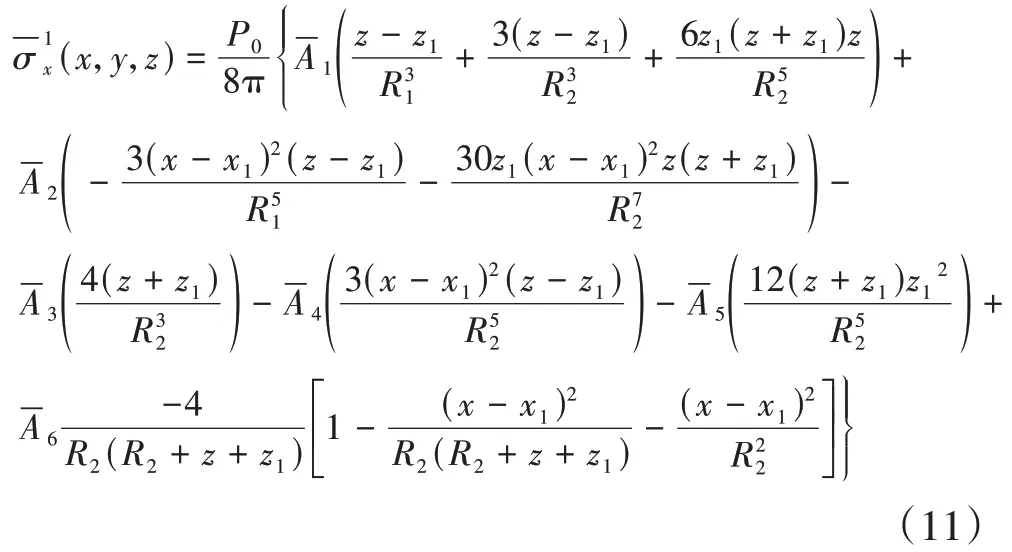
同理可得x方向水平卸荷引起临近桩x方向的附加荷载时域解及y方向水平卸荷引起临近桩x方向的附加荷载时域解，限于篇幅，不再赘述.

2.2 开挖引起的邻近桩基总附加应力

桩基受力模型如图2 所示，基坑与邻近桩基的水平距离为L0，基坑开挖尺寸为B×L×H，桩基长度为L1，在基坑中心点建立坐标系，对基坑四个侧壁及基坑底面进行编号，分别为①、②、③、④、⑤.魏纲等［24］综合比较了张治国等［25］和姜兆华等［26］的工作，认为Mindlin 解只适用于弹性半空间体，远离桩基一侧的另外一个基坑侧壁由于土体已开挖，无法传力，提出了开挖卸荷条件下邻近地基中一点考虑坑底及三个坑壁卸荷作用叠加的附加应力计算方法.本文选取邻近桩基的三个侧面及基坑底面①、③、④、⑤引起的邻近桩附加应力进行计算.

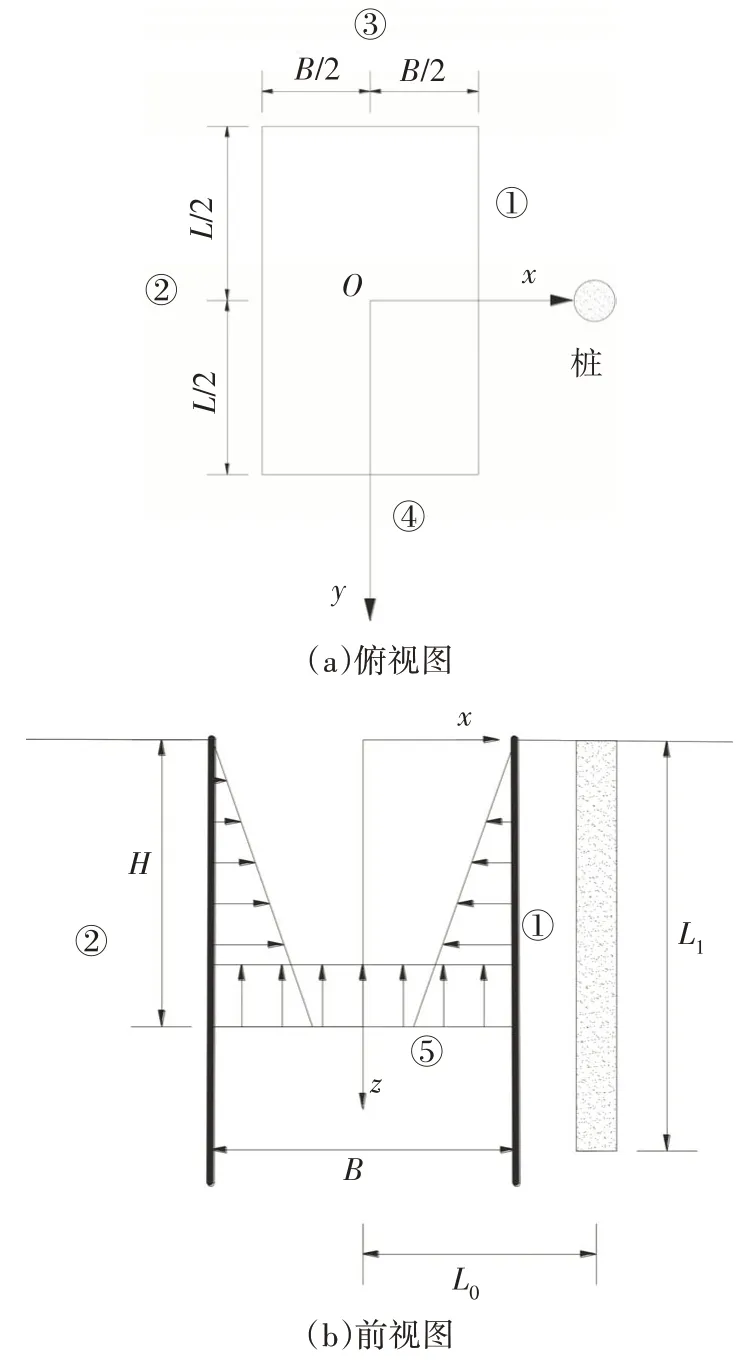
图2 基坑-桩基相对位置示意图Fig.2 Diagram of relative position between pile and excavation

对邻近桩基附加应力的计算，做以下假定：1）地基土为均质土且各向同性；2）在计算基坑开挖卸荷引起邻近土体的附加应力时忽略桩基存在时的影响；3）不考虑基坑降水作用和基坑开挖时的空间效应.

取编号⑤的基坑底面一微小单元，在此单元上所受均布力为P0=γhβ，其中γ为开挖土层深度h范围内的重度加权值，β为折减系数，具体取值可以参考姜兆华等［26］的研究.

通过对受力面积进行积分计算即可得开挖范围内，基坑底部⑤卸荷对邻近桩基的水平附加应力值为：

取编号为①的基坑侧壁上一微小单元，在此单元上所受均布力为P1=γhβK0，K0为侧压力系数，由K0=μ/(1-μ)求得.通过对开挖卸荷面积进行积分计算即可得到开挖范围内，基坑侧壁①卸荷引起邻近桩基的水平附加应力值为：

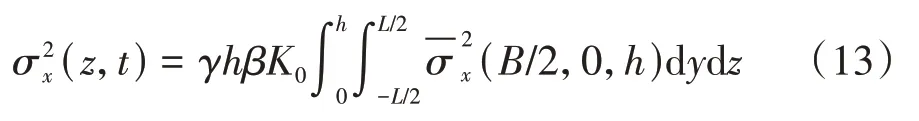
同理可得基坑侧壁③和④引起邻近桩基的水平附加应力为：

将基坑坑底卸荷效应与坑壁卸荷效应引起的水平附加应力进行叠加，即可得到基坑开挖卸荷引起的邻近桩基轴线上的水平附加应力值：

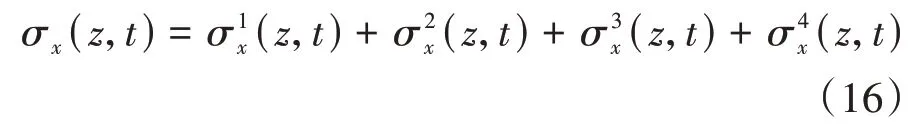
3 基坑开挖引起邻近桩水平变形时域解

将临近桩看作放在Pasternak 地基上的Timosh⁃enko梁，计算模型如图3所示.

图3 计算模型Fig.3 Calculation model

根据Timoshenko 梁理论，弯矩和剪力有如下关系：

式中：EI为桩基的抗弯刚度；κGA表示桩基的剪切模量，其中A为桩截面面积，G为桩基的剪切模量，κ为剪切系数，当桩基截面为圆形时取0.9；w为桩挠度；θ为桩截面转角；M、Q分别为桩基所受的弯矩与剪力.

取桩的一微分单元进行受力分析，其受力如图4所示.

图4 桩微段受力示意图Fig.4 Forces analysis of pile element

根据图4建立平衡微分方程可得：

式中：q(z，t)为基坑开挖卸荷时对桩的附加荷载，由式（16）求得；D为桩基直径；p(z，t)为地基反力，由Pasternak地基理论可得：

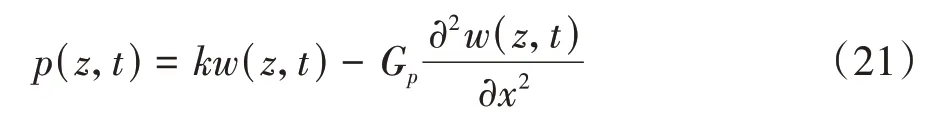
式中：k和Gp分别为地基反力模量和剪切层刚度.

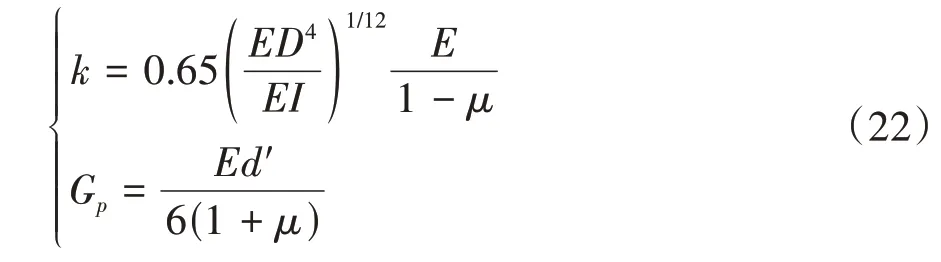
式中：E和μ分别为土体的卸荷模量和泊松比，文献［22］对其取值进行确定与修正；d'为桩土间剪切层厚度；D为桩基直径.

将公式（17）（18）（21）代入公式（19）（20），可得基坑开挖卸荷条件下邻近桩基水平变形的位移控制微分方程，方程是一个含时间变量的非齐次四阶常微分方程，直接求解较为复杂，为了简化求解过程，对其进行Laplace变换，可得：

式中：wi(z，s)及qi(z，s)分别为wi(z，t)和qi(z，t)的Laplace变换.

根据标准差分原理，将公式（23）写作标准差分形式为：

假设桩基为摩擦桩，其两段自由，弯矩和剪力均为0，即：

将公式（24）写成矩阵形式：

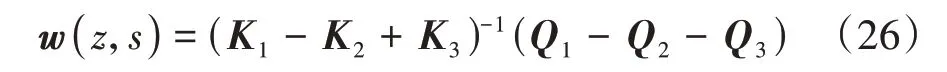
式中：K1为桩基位移刚度矩阵；K2为桩基剪切刚度矩阵；K3为桩基抗弯刚度矩阵；［w（z，s）］为桩基水平位移矩阵；Q1、Q2、Q3为附加荷载列向量，结合边界条件（26）即可得到各矩阵的表达式.

对公式（26）进行Laplace 逆变换，即可得到基坑开挖卸荷对临近桩水平位移影响的时效分析.在已知基坑开挖卸荷对邻近桩基附加荷载的情况下，结合公式（27）即可得到基坑开挖卸荷条件下邻近桩基水平位移的时域解.值得注意的是，令桩基的剪切刚度κGA足够大时，桩基的剪切变形趋近于0，Timosh⁃enko 梁退化为Euler-Bernoulli 梁矩阵；当Gp为0 时，Pasternak地基退化为Winkler地基.

4 方法验证

4.1 地基应力时域解的正确性验证一

本文提出的应力时域解是基于Mindlin 解，这意味着时域解可以退化为经典Mindlin 解［23，27］.在t=0时有Eα(0)=1，土体并未发生蠕变变形，取G=G1，可得到弹性应力解公式，将弹性模量关系ν=（3K-2G）/（6K+2G）代入弹性解中即可得到公式退化结果和Mindlin 解［公式（5）］一致；同理当时间t趋于无穷大时有Eα(∞)=0，土体蠕变变形达到最大值，此时G=G1G2/（G1+G2）同样可得退化结果和经典Mindlin 解一致，验证了本文分数阶应力时域解的正确性.

4.2 地基应力时域解的正确性验证二

祝彦知［28］基于三参数黏弹性模型推导了半无限弹性体内作用有竖向和水平向集中应力时，空间内某一点的应力和位移分量的黏弹性解.取参数：集中力P0为100 kN，分数阶α为1，剪切模量G1为10 MPa，剪切模量G2为10 MPa，体积模量K为15 MPa，黏滞系数η为30 MPa·d；集中力作用点（0，0，0），应力点（1，1，1），其结果如图5所示.

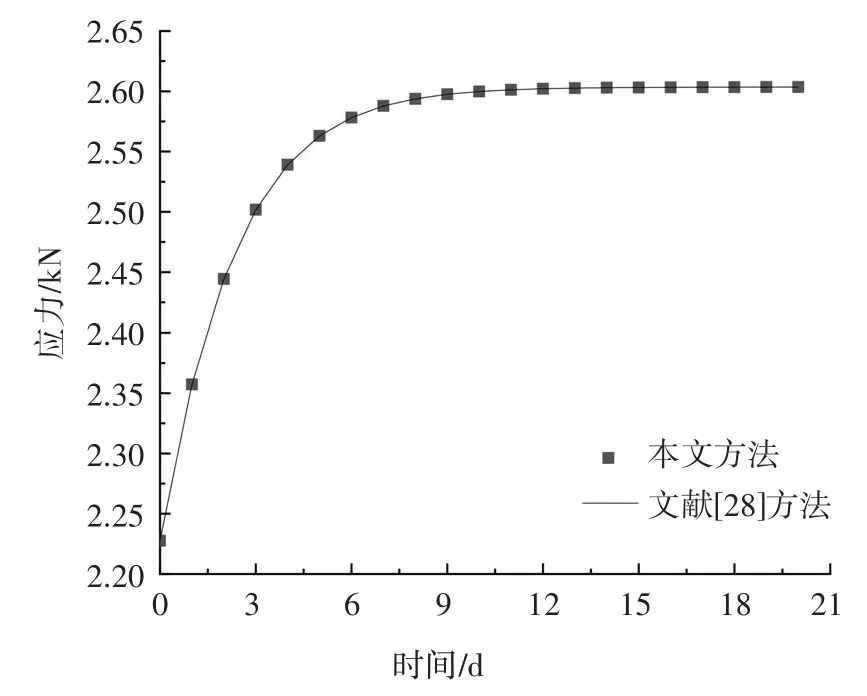
图5 应力-时间关系曲线Fig.5 Stress-time curve

从图5 可以看出本文解与文献［28］有较好的一致性，因为当分数阶Merchant 黏弹性模型参数α取1时，根据Gamma函数的性质有：

此时本文分数阶黏弹性模型退化为整数阶三参数模型，与文献［28］所取得应力解形式一致.能够说明本文分数阶应力时域解的正确性.

4.3 软土地基单桩模型的正确性验证

Zhang 等［14］将桩看作Pasternak 地基上的Euler-Bernoulli 梁，基于Boltzmann 黏弹性模型推导出软土地基中基坑开挖对邻近桩水平位移影响的时效影响.相关参数如下：基坑尺寸为30 m×20 m×10 m，桩基长度18 m，桩径0.9 m，桩基弹性模量20.5 GPa，桩径中心线距离基坑的水平距离为20 m.土体泊松比0.33，土体密度为1.95 g/cm3，剪切层厚度15 m，黏弹性模型参数G1为0.86 GPa，G2为0.62 GPa，体积模型K为0.68 GPa，黏滞系数为16.7 GPa·d.

此时分数阶Merchant 黏弹性模型退化为整数阶Boltzmann 黏弹性模型，同时令桩基的剪切模量趋于0，Timoshenko 梁退化为Euler-Bernoulli 梁模型，此时退化后模型所需参数和文献［14］所需参数一致.取与文献［14］一致的参数，分数阶α为1.取桩身深度z为2.7 m、7.2 m、9.9 m、14.4 m 处桩身水平位移进行分析.由图6 可知，本方法计算结果与文献［14］的结果有较好的一致性，可以证明本文解是准确的.目前，传统的算法是将桩基简化为放置在Winkler 地基上的Euler-Bernoulli 梁（简称EB-W 模型），通过与本文方法和文献［14］对比可知，本文方法和文献［14］方法解得的桩基水平位移小于EB-W 模型结果，其原因为Pasternak 地基相比于Winkler 地基考虑了地基弹簧之间的相互剪切效应，反映了地基土介质的连续性，进一步说明了Pasternak 地基的优势.同时，从图6 可以看出，当考虑软土地基的蠕变时，桩基水平位移随时间逐渐增加，最终增长量分别占不考虑流变工况下桩基横向变形的27.98%、29.10%、32.48%、49.36%，表明软土地基蠕变对桩基的水平位移影响较大，在工程实际中不能忽略.

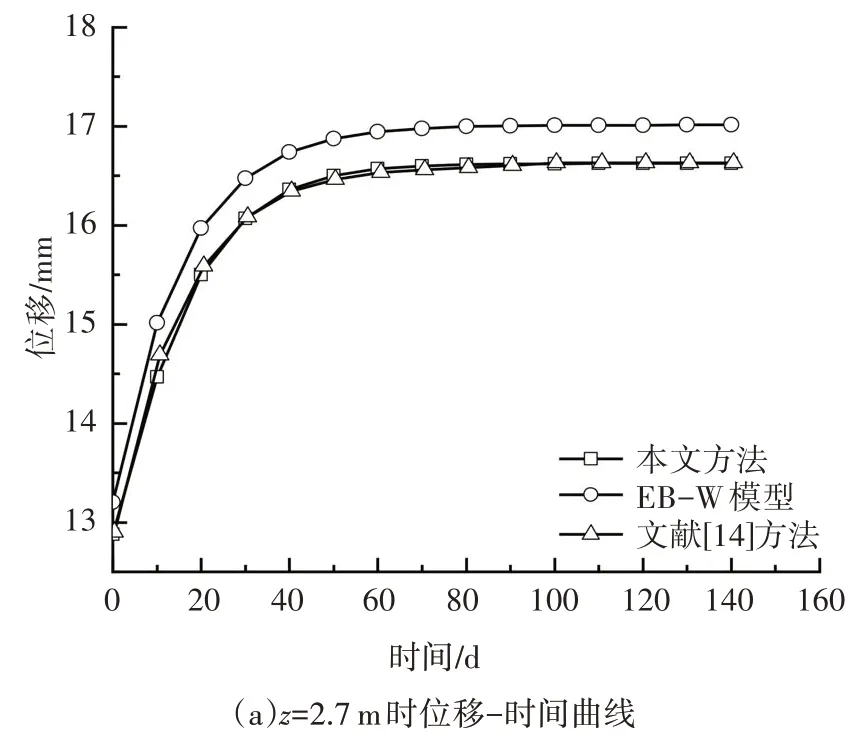
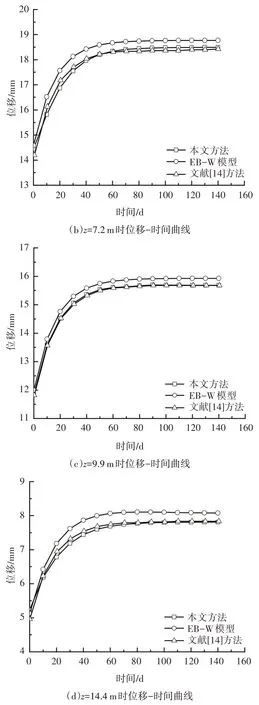
图6 桩基水平位移-时间曲线Fig.6 Relation curves between pile horizontal displacement and time

5 参数分析

上述文献数据对比验证了本文所提理论的正确性，在此基础上对分数阶Merchant 黏弹性模型参数进行分析.计算模型基本参数为：基坑开挖尺寸30 m×20 m×10 m，桩基弹性模量20.5 GPa，桩身剪切刚度为40 GPa，桩径中心线距离基坑的水平距离为2 m，桩径0.9 m，桩长20 m.Merchant 黏弹性模型参数取值为：G1=8.6 MPa，G2=6.2 MPa，K=6.8 MPa，η=160 MPa·d，α=0.6.土体卸荷模量E为7.987 MPa.因为本文提出的是桩基水平位移与时间有关的解，所以在对部分参数进行分析时选取桩基处某一特定的点进行，选取图2坐标系中桩身坐标（12，0，10.7）处桩基水平位移随时间的变化进行分析.

为分析分数阶Merchant 黏弹性参数对桩基水平位移的影响，分别对参数取不同的值进行分析.将基坑开挖后桩基水平位移随时间增长过程分为初期和末期.由图7 可知，在基坑开挖后初期，G1越大桩基水平位移越小.在本构模型中，G1为模型的瞬时变形参数，主要与土的初始变形能力有关，控制桩基的初始变形能力.黏弹性模型参数的获取可以参考文献［29-30］的方法，利用三轴固结实验获得土的蠕变曲线，再根据应力松弛公式拟合分数阶黏弹性模型参数.在剪切模量G1较小的基坑工程中，应加强开挖后初期基坑和邻近桩的变形监测.

图7 剪切模量G1对桩身水平位移的影响Fig.7 Influence of shear modulus G1 on horizontal pile displacement

由图8 可知，当G2取不同值时，在开挖后初期桩基水平位移相同，当桩基水平位移随着时间增加时，G2越大，桩基水平位移增加越少，最终变形越小.主要是因为剪切模量G2是黏弹性模型的延时变形体参数，与土的延时变形能力有关，控制着土体蠕变变形的极限值.

图8 剪切模量G2对桩身水平位移的影响Fig.8 Influence of shear modulus G2 on horizontal pile displacement

从图9 可以看出，体积模量对临近桩基水平位移的影响较明显.体积模量K越大，桩基水平位移越大，桩基位移增加的幅度越小.体积模量K对临近桩水平位移的影响是不可忽视的.

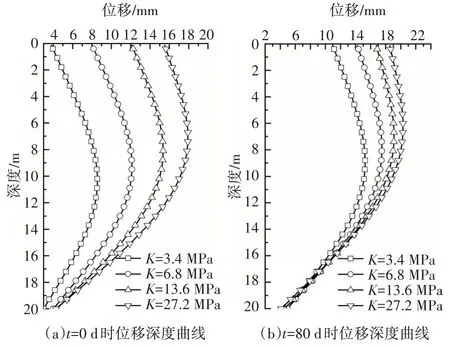
图9 体积模量K对桩身水平位移的影响Fig.9 Influence of bulk modulus K on horizontal pile displacement

从图10可以看出，当η取不同的值时，基坑开挖对临近桩水平位移的初始值和最终累计变形是没有影响的，但是对达到水平位移极限值所需要的时间有显著影响.η越大，达到极限值的时间越长，主要是因为黏滞系数η是黏弹性模型的延时变形参数之一，控制着土体的延时变形速率.

图10 黏滞系数η对桩身水平位移的影响Fig.10 Influence of coefficient of viscosity η on horizontal pile displacement

从图11可以看出，当取不同α值时，基坑开挖引起的临近桩水平位移按照发展时间可分为两个部分，分界点为图11 线段的交叉点，在第一部分临近桩水平位移随着α的增大而减小，在第二部分临近桩水平位移随着α的增大而增大.图中所示的交叉现象是由黏弹性模型中的Abel 阻尼元件导致的，也是分数阶模型相比于传统模型的优势所在，即能更准确地模拟材料的流变特性.当α=1时，Abel阻尼元件退化为牛顿流体；当α=0 时，Abel 阻尼元件退变为弹性体.因此，当α取较小值时，土体的力学性质主要由剪切模量G2控制，桩基水平位移在第一部分有较大位移值，在第二部分位移发展缓慢；当α取较大值时，土体的力学性质主要由黏滞系数η控制，桩基水平位移在第一部分有较小位移值，在第二部分位移发展较快.

图11 分数阶α对桩身水平位移的影响Fig.11 Influence of fractional diffusion order α on horizontal pile displacement

6 结论

1）本文通过引入三维分数阶Merchant 黏弹性模型并将既有桩基简化为Pasternak 地基中的Timosh⁃enko 梁，得到基坑开挖引起邻近桩基水平位移时域解.结合相关文献验证了本文模型的正确性，通过计算表明土体的蠕变变形对桩基的水平位移影响较大，在实际工程中不能忽略软土蠕变的影响.

2）分数阶Merchant 黏弹性模型参数G1对开挖完成后初期桩基水平位移影响较大，决定基坑开挖完成后初期桩基水平位移值，开挖完成后初期桩基水平位移随着G1的增大而减小；剪切模量G2对开挖完成后末期桩基水平位移的极限值影响较大，决定位移的最大值，开挖后末期桩基水平位移最大值随着G2的增加而减小.

3）桩基水平位移在基坑开挖完成后初期和末期位移均随着体积模量K的增加而增大；黏滞系数η与桩基水平位移变化的速率有关，η越大，桩基位移达到最大值时所需的时间越久；分数阶α对桩基水平位移影响按时间可分为两个部分，在第一阶段桩基位移随着α的增大而减小，在第二阶段桩基位移随着α的增大而增大.