基于IMOA-MSSK-means 的风电场机组遗传优化出力策略研究
2022-12-03王存旭
裴 根,王存旭,赵 琰
(沈阳工程学院a.电力学院;b.自动化学院;c.新能源学院,辽宁 沈阳 110136)
随着现今化石能源的过度开采以及环境污染等问题愈发严重,发展可再生能源成为了解决这些问题的主流趋势。而风能作为一种安全无污染的可再生能源,更是持续不断地渗透到各个地区的电网中。但是风电拥有着很强的随机性和间歇性,这给电力系统整体的安全稳定运行带来了严重的影响[1-2]。随着风电大规模并入电网,如果想要消减其不稳定性对电网的影响,风电场本身需要具备一些可以减弱自身对电网造成不利影响的能力,以此来保证电网可以保持运行在稳定状态且降低出现风电场退出运行的情况发生。
针对风电场发展越来越迅速,规模越来越大而导致的功率优化调度困难的问题,这不仅仅需要研究如何更好地优化风电场内的功率分配问题,而且研究风电场内各个机组间的功率优化分配也显得至关重要[3]。目前,国内外一些学者已经对风电并网的风电场内机组的优化策略进行了深入的研究。文献[4]提出了一种调度机组的调峰方法。首先,将厂内所有的调度机组进行组合分配,以此来确定哪些机组需要在何时出力;其次,根据电网总的调度指令对分配后的组合机组进行出力优化,确定每一台机组的实际出力值。文献[5]提出了利用粒子群算法和网格分析法建立模型,以并网处的电压和风电机组端电压的差值最小为目标来进行功率优化,并用仿真实验验证了此方法可以使机组出力更加准确,更好地控制机组出力。文献[6]提出了利用遗传算法优化有功网损和节点电压越限之和,得出其最小值,并通过仿真实验验证了该方法可有效调节风电机组的输出。文献[7]提出了一种以优化控制器来实现输出功率偏差量最小的方法,通过风电场在不同风速下运行特性的不同,以功率输出偏差量最小为目标函数,实现风电机组的出力优化。综上所述,国内外大部分学者都没有考虑风电机组在不同风速下特性不同的问题,即使对场内机组进行了分类,但是却没有考虑到地势地形也会对机组分类造成影响。
针对上述问题,本文提出了一种基于IMOAMSSK-means 的风电厂机组遗传优化出力策略方法。通过该聚类分析方法对风电场内机组特征矩阵进行分类,由分析结果判断出最合适的机组来参与接下来的功率分配任务,然后用遗传算法对参与功率分配的机组进行寻优分析,寻找最佳的机组运行组合出力来优化风功率数值的分配,并通过华北某风电场预测数据进行仿真实验,验证该方法的可行性。
1 基本原理概述
1.1 磁优化算法
磁优化算法(MOA)是一种跟磁场力有关的算法,由磁性粒子构成,粒子的分布如图1 所示。根据冯诺伊曼邻域结构,其拥有S×S个磁性粒子,圆型结构里面的数字表示各个磁性粒子对应的当前位置。记第i行第j列的磁性粒子为Xij,则Xij的相邻粒子[8]为

图1 磁性粒子分布
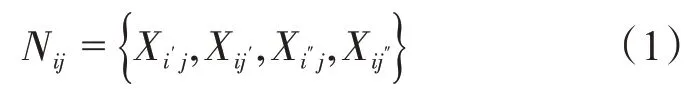
式中,i=1,2,···,S;j=1,2,···,S;Xi′j、Xij′、Xi″j、Xij″分别代表与当前磁性粒子对应连接着的4 个方向(上下左右方向)的磁性粒子,且满足:

磁优化算法的原理是通过粒子与相邻粒子之间的相互吸引作用,确保该算法拥有更好的全局搜索能力。磁优化算法的具体实现流程如下:
1)首先进行初始参数设置,其中设最大迭代次数为Maxitr,磁性粒子个数为S,磁性粒子速度Vitr的初始值为0,假设磁性粒子为N维,则磁性粒子的位置初始化如下:
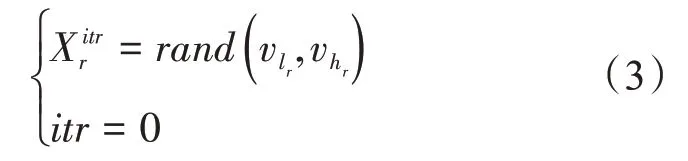
式中,rand是[0,1]之间的随机数发生器;vlr和vhr表示第r维的最小值和最大值,其中r=1,2,···,N;itr是当前的迭代次数。
2)求出各个粒子的目标函数值,然后对磁性粒子进行标准化:

3)对磁性粒子的质量进行计算:

式中,α和β都是常数。
4)计算相邻的粒子对粒子吸引力的合力,如计算第i个磁性粒子合力:

其中,D是磁性粒子i与相邻磁性粒子j之间的距离,公式如下:

5)对各个磁性粒子的加速度、速度及位置进行更新计算:
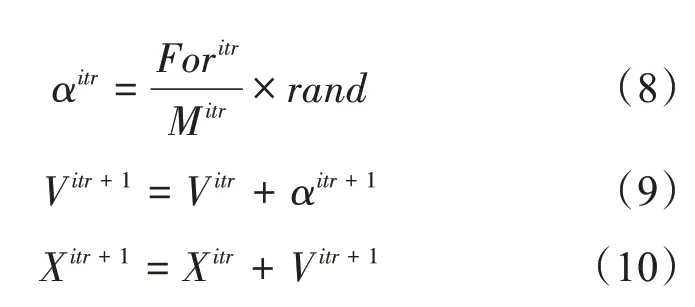
6)最后进行判定是否达到初始设置的最大迭代次数,如果达到,则输出结果;如果未达到,则当前迭代次数加1,继续重复2)~5)步的迭代。
1.2 改进磁优化算法
传统的MOA 算法中磁性粒子的初始值是随机选取的,这种随机性很大概率会导致寻优的结果不准确,陷入局部最优解的情况。为了解决这个问题,本文引入了一种差分优化的策略来改进磁优化算法,即IMOA。
引入差分优化策略就是对目标函数假设为gbt的最优粒子进行变异处理,通过这种方式可以有效地对其邻域空间进行充分搜索,比起传统MOA,可以大大降低出现局部最优解的情况。当使用差分优化算法对假设为gbt的最优粒子进行扰动处理时,由于该算法有许多不同的向量生成策略和规定,为更好地满足本算法的需要,变异策略为
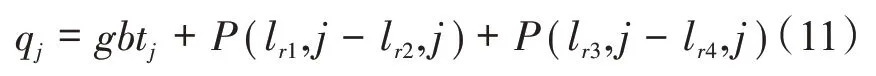
式中,r1、r2、r3、r4 代表区间[l,S]上4 个随机整数;P为尺度系数;j为磁性粒子的维度;qj为扰动后的值。
用交叉处理得出试验向量gbt*:

式中,CR为交叉概率;jrand为在规定的维度区间中随机的整数值。
由于差分进化算法用的是贪心算法原则,通过只留下精英粒子的策略来优化传统算法出现局部最优解的情况。所以,当遇到最优数值问题时,应将原始向量gbt和试验向量gbt*的目标函数值进行比较,从而选择出最优的向量,如下式:

1.3 流形K均值聚类
传统K均值算法以欧式距离为相似性度量,对于处理高维数据的效果不是很理想[9]。因此,流形K 均值聚类算法(MSSK-means)继而被提出,用流形距离代替传统算法的欧氏距离,可以更准确地处理高维数据,聚类效果更加理想。将流形距离计算看成沿流形上所有局部欧氏距离的最短路径,则xi与xj间的流形距离为

式中,L表示流形上两邻近点的距离;k为xi的邻域个数;(pk,pk+1)∈E,1 ≤k≤b-1,k为两点之间的路径。
流形距离和欧氏距离相比较而言,流形距离可以更好地表明各数据点的分布,更清楚地表达高维复杂数据之间的特征联系。所以,在处理高维数据时,以流形距离作为度量标准进行聚类分析,能有效提高聚类效果。如图2 所示,A、B两点间的直线距离和曲线距离分别为欧式距离和流形距离。从图中可以看出:相比于欧氏距离,流形距离的聚类能力更为出色。

图2 欧氏距离与流形距离
1.4 遗传算法
遗传算法由美国的Holland 教授在1975 年提出[10]。作为一种高度并行、概率化的优化算法,通过复制、交叉、变异将问题的解编码表示成染色体群一代代不断地进化,最终收敛到最适应的群体,从而求出最优解。其拥有着收敛性强、有潜在并行性、过程简单和强大的全局搜索能力的优点,尤其适用于求解组合优化问题。面对风电场机组这种庞大的数据问题,遗传算法正是最好的解决问题的工具之一。
2 IMOA-MSSK-means的风电场机组遗传优化出力策略
2.1 风电机组特征矩阵
由于风速和风向对风场内机组输出功率有着较大的影响,而且各个机组的距离不一样,所在的地理位置、地貌可能有所不同,这些因素都极大地影响着机组出力大小。本文假设风力风电机组只受风速影响,所选用的风电机组的特征矩阵是使用其输出功率的平均值和标准差计算出来的[11]。
输出功率平均值公式为

式中,Piave为风电场第i台机组在j=1,2,3,…,N时段输出功率的平均值。
输出功率标准差公式为

式中,Pisd为风电场第i台机组在j=1,2,3,…,N时段内输出功率的标准差。
将上述数据归一化处理,以求取机组输出功率特征矩阵。数据归一化公式为

式中,Piave(0-1)为第i个机组输出功率平均值归一化的值;Pisd(0-1)为第i台机组输出功率标准差归一化的值;Pavemin为风电场内各机组输出功率平均值的最小值;Pavemax为风电场内各机组输出功率平均值的最大值;Psdmin为风电场内各机组输出功率标准差的最小值;Psdmax为风电场内各机组输出功率标准差的最大值。
2.2 风电机组指标
为尽量降低风速对机组出力产生的影响,同时不增加冗余机组运行损耗与备用机组的启停损耗,提出优化目标函数为
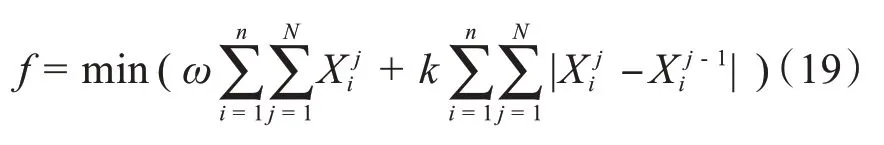
式中,X表示由0和1组成的n×N维矩阵,0表示第j时间段内第i台风机处于停机状态,1 表示第j时间段内第i台风机处于运行状态;N为风电机组优化调度的时间;n为风电场内风电机组总台数;ω表示风电场运行相对损耗指标的权重系数;k为风电场启停相对损耗指标的权重系数。
风电机组优化调度的约束条件如下:
1)功率平衡约束

2)机组出力上下限约束

3)旋转备用约束

2.3 IMOA-MSSK-means聚类
传统的K-means 算法对于聚类中心初始值敏感,不同聚类数目得到的聚类效果不同,并且容易陷入局部极值。针对这些问题,本文提出了一种基于IMOA-MSSK-means 的聚类算法。为解决传统MOA 磁性粒子可能出现陷入局部极值的情况,引入差分优化策略,并选择用流形距离代替欧氏距离以便获得最佳的聚类效果[12]。具体步骤如下:
1)首先对所采取的数据进行统一的归一化处理,并初始化S个特征矩阵,将计算得到的S个聚类中心初始值集合编码作为S个磁性粒子的值,设置最大迭代次数为Maxitr;
2)设置磁性粒子的初始速度为Vi,其值为一个随机的0~1的数;
3)根据式(4)计算各个磁性粒子的磁场强度Bi;
4)通过式(5)~式(7)分别计算每个磁性粒子的质量值、距离和所受的合力;
5)更新磁性粒子加速度、速度与位置值;
6)判断是否达到最大迭代次数,若是则输出结果,否则重复步骤3)~6);
7)最终获得的最优磁性粒子是聚类中心值,并将其赋给MSSK-means进行负荷曲线聚类分析。
2.4 基于IMOA-MSSK-means聚类的遗传寻优
本文运用如下6 个步骤对上述聚类结果进行遗传寻优。
1)初始化遗传算法参数。
2)用IMOA-MSSK-means 聚类对所有机组进行聚类分析,选择出最适合调度的机组进行遗传算法的染色体编码,并使用随机的方式进行机组组合,将这种组合作为遗传算法的初始种群。
3)将计算出初始种群中机组的相对运行损耗与相对启停损耗之和作为适应度函数。
4)分别对初始的群体进行选择、变异和交叉,用这种方式来产生下一代种群的机组组合。
5)判断是否满足最大迭代次数的终止条件,若满足便输出结果,不满足则返回步骤3)继续迭代。
6)求取比较各个机组组合的目标优化函数后,选择目标优化函数值最小的机组组合作为最优解。
寻优过程就是获得风电场机组的基本参数后,用IMOA-MSSK-means 方法进行风电场机组的聚类,由分析结果判断出最合适的机组来参与接下来的功率调度分配任务[13],再用遗传算法对调度机组组合进行判定寻优,选取最优的机组运行组合。通过这种方式可以更加合理地调配风电场的功率输出,以达到增强调度指令执行力的作用[14]。
3 应用实例
本次实验使用华北某风电场22 台1.5 MW 的风力发电机24 h 预测数据,将24 h 分为6 个时段,并使用MALTAB 仿真软件进行仿真实验分析。本次实验所用的风电场22 台机组的24 h 出力预测值,如表1所示。

表1 22台风力发电机24 h预测出力值 MW
对该风电场24 h 风机的历史数据进行特征矩阵提取,根据平均值特征值和标准差特征值的差别将22 台机组分为4 类,并使用MALTAB 进行聚类仿真,具体结果如图3和表2所示。
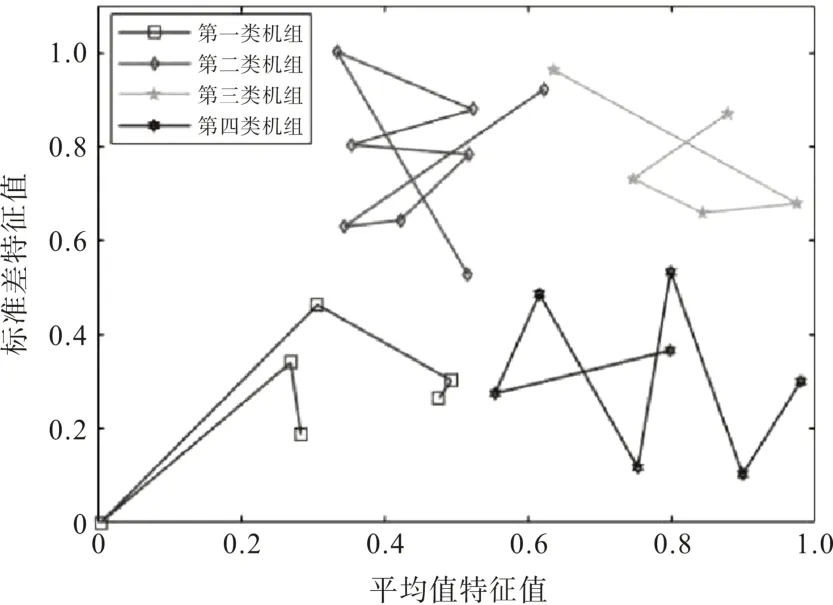
图3 22台风力发电机组聚类仿真结果

表2 22台风力发电机组分类结果
由图3 和表2 可知:第2 类机组的平均值特征值低于其他3 类机组,但标准差特征值高于其他3类机组,这说明第2类的7台机组出力较低,且波动幅度较大,因此是调度机组的最佳选择。对第2 类机组进行遗传寻优来寻找最佳机组组合。本次遗传算法的初始种群、变异概率、交叉概率、遗传代数和迭代次数分别为50、0.05、0.5、3、300,实验结果如表3所示。

表3 7台风电机组最优启停机组合
由表3 可以清楚地看出:为了达到目标优化函数值最小这一目标,机组17 在本次调度阶段一直处于未参与的状态,而机组20 在本次调度阶段后2 个时段也没有参与。在求取了本次7台风电机组最优的组合后,使用风功率预测公式(24)求出每台机组的具体出力值,得到7 台风电机组输出功率的最优结果,如表4所示。
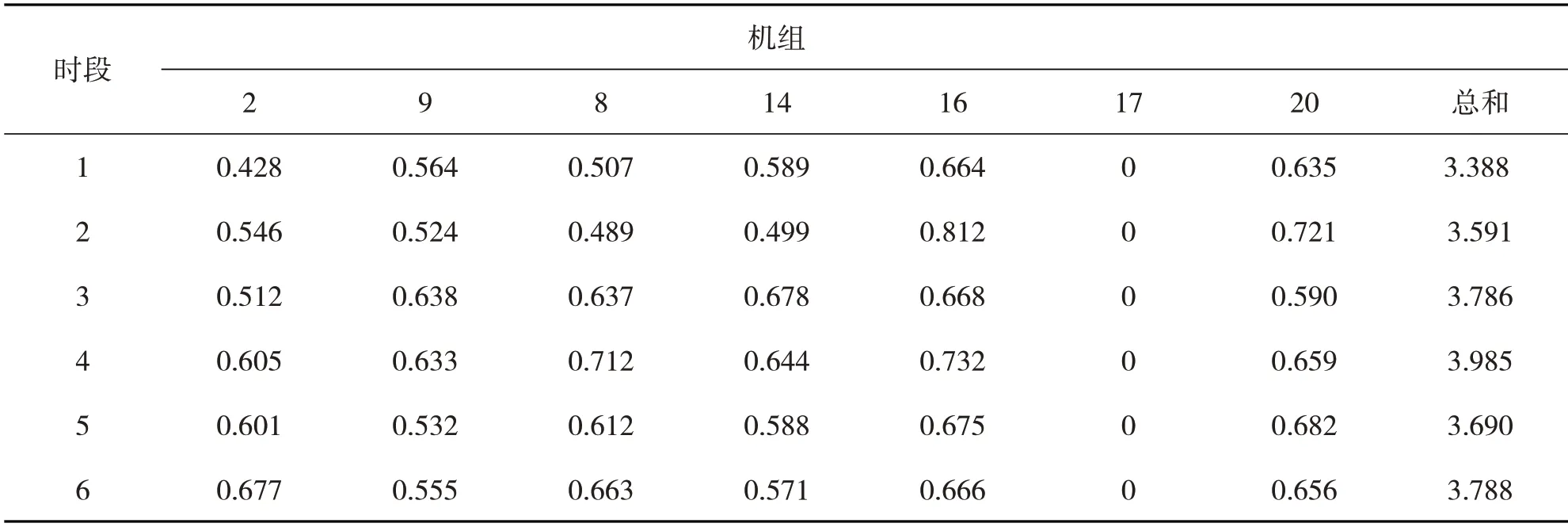
表4 7台风电机组最优出力结果 MW
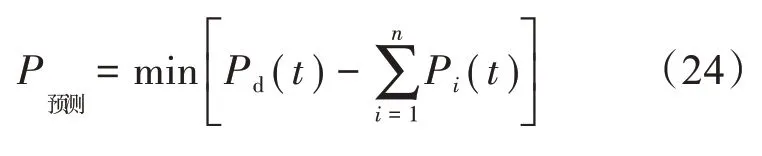
式中,Pd(t)为6 个时段7 个机组所需调节的功率值;Pi(t)为第i台风力发电机组出力。
由本文提出的方法所获得的最优出力与传统K 均值-遗传和模糊-遗传所求得的最优出力与调度指令进行综合对比分析,如图4所示。
由图4可以看出:本文所提出的策略的效果优于上述提到的传统方法,在本文提出的控制策略下,6个时段7台机组的总出力分别为3.388 MW、3.591 MW、3.786 MW、3.985 MW、3.690 MW、3.788 MW,与6 个时段的调度指令3.4 MW、3.6 MW、3.8 MW、4.0 MW、3.7 MW、3.8 MW 相差甚微,可以看出本文提出的风电机组出力优化策略效果显著,可以有效地进行功率分配,且分配后的风电场出力总和与总调度指令差距很小。

图4 风电机组出力与调度指令对比
4 结语
本文针对风电出力的随机性和波动性所导致的功率优化调度问题,提出了一种基于IMOAMSSK-means 的风电厂机组遗传优化出力方法。根据历史数据求出各个风电机组的特征矩阵,并提出一种IMOA-MSSK-means 聚类分析方法,选出更适合参与功率分配调度的机组。用全局寻优性强的遗传算法找出适合调度的机组进行最优组合。通过华北某风电场的短期风功率预测数据对所提出方法进行了算例仿真验证,通过实验结果可以清楚地看出:本文所提出的方法对风电场机组的功率合理分配效果卓越,分配后的总出力与调度指令相差甚微,有效地提高了调度指令的执行力,验证了所提出的策略的可行性。
