基于极限学习机的碳酸盐岩储层测井评价方法<br/>——以川中北部GM区块灯二段为例

基于极限学习机的碳酸盐岩储层测井评价方法
——以川中北部GM区块灯二段为例

2022-12-03徐鹏宇周怀来刘俊平陶柏丞

大庆石油地质与开发 2022年6期

徐鹏宇周怀来赵霞周捷刘俊平陶柏丞

（1.成都理工大学能源学院，四川成都 610059；2.成都理工大学地球物理学院，四川成都 610059；3.成都理工大学油气藏地质及开发工程国家重点实验室，四川成都 610059）

0 引言

在油气行业储层评价中，储层类型划分尤其重要，是区别各类有效储层及非储层的关键，一直以来对碳酸盐岩的储层评价是油气勘探开发的焦点与难题。近年来，不少学者对碳酸盐岩储层进行了许多深入的研究，主要为碳酸盐岩储层类型的划分［1-2］、识别［3-4］以及特征分析［5］等。储层类型的精细解释及评价有利于提高采收率，为油气勘探开发提供必要的支撑。

碳酸盐岩储层之所以孔隙结构复杂、非均质性强［6］，其原因是该类储层通常具有孔隙、孔洞及裂缝空间共同发育的特征。因此，在碳酸盐岩中寻找优质储层的关键就在于如何科学地进行储层分类及识别。宋修章等［7］通过综合运用产能系数法、经验统计法和气藏工程法等方法确定出储层物性下限，根据不同的物性数据阈值对储层类型进行了划分，该方法建立在物性参数的连续准确性基础上，但仅依靠常规测井资料对碳酸盐岩物性参数进行准确解释仍然是一个难题［8］。近年来，随着测井技术的不断进步，许多学者利用常规测井和成像测井相结合的方式识别储层类型、岩性及裂缝等［9-11］，通过系统归纳常规测井和成像测井的响应特征，对储层进行定性和定量评价。人工总结常规测井响应特征大多数情况依赖于解释人员的现场经验，实际操作中难免存在偏差。一些学者将数学地质方法应用于对评价目标敏感的常规测井参数的计算中，如因子分析、主成分分析、模糊聚类分析等。郭建宏等［12-13］将灰色系统理论应用于常规测井曲线，利用改进的斜率关联度法获取对评价目标敏感的测井曲线序列，能更充分开发测井曲线与评价目标的相关性，科学地获取“核心数据序列”。随着机器学习的不断更新换代，支持向量机、神经网络［14］、决策树、随机森林、XGBoost［15］等代表算法和一些改进算法被广泛地应用于多参数融合分类及回归中。何健等［16］将近似支持向量机（PSVM）算法应用于多地震属性对岩层裂缝带发育程度的分类中，充分利用了其运算速度高效、分类效果显著等特性，并显著提高了储层裂缝带的预测精度。陈芊澍等［17］证实了极限学习机（ELM）算法在一些特定情况下运算速度及分类精度均略高于PSVM 算法。ELM 算法同时具备训练速度快、泛化能力强及鲁棒性高等特点，其仅有一个隐藏层的简单结构，相较于PSVM 算法能减少人为干预，发挥出模型的真实性能［18］。

本文以川中北部GM 区块灯影组灯二段测井、录井、岩心等资料为基础，采用斜率关联度、极限学习机分类算法和滑动窗口等技术建立储层类型识别模型，融合极限学习机回归算法、流动单元指数和离散岩石聚类等方法建立物性参数解释模型，结合油井的日产气量评价标准来验证该方法的可行性，以期实现对研究区储层精细分类评价及物性参数解释，为该区油气藏的高效开发提供支撑。

1 方法原理

1.1 斜率关联度

一般关联度法对样本数量小且离散性强的数据有较强的实用性，其原理是通过对比各序列与目标序列曲线的形状，如果序列间关联度越大，则2 条曲线的几何形状越相似［19］。实际使用时，普通的关联度法误差较大，许多学者对此提出了改进，马保国等［20］提出的普通斜率关联度法的原理是根据不同序列上各序列段斜率的相似程度，计算各序列间关联度的大小，斜率越相似则关联度越大，反之则越小。其后，曹明霞［21］在此基础上进行了改进，对斜率的正负进行了计算，使其既能反映正关联也能找到负关联，极大地提高了评价的精确性。规定某参考序列向量x0与另一对比序列向量xi，其形式分别为：

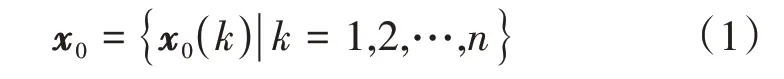
式中：x0（k）——长度为k的参考序列向量；xi（k）——长度为k的对比序列向量。

改进的斜率关联法计算公式［22］为

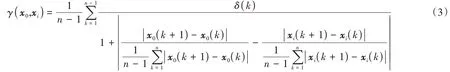
式中：γ（x0，xi）——x0与xi的关联度；δ(k)——引入的改进函数。

δ(k)反映序列间的正负关联性，当[x0(k+1) -x0(k)][xi(k+ 1) -xi(k)]≥0 时，δ(k) = 1，当[x0(k+1)-x0(k)][xi(k+1)-xi(k)]＜0时，δ(k)=-1。

1.2 极限学习机

W.Y.Deng 等［23］提出将改进的单隐层前馈神经网络算法定义为ELM。ELM 通过随机赋值的方式对输入权值和偏置进行设置，并根据“最小二乘法”原理，利用Moor-Penrose 伪逆矩阵计算输出权值。对比传统的基于梯度下降算法求极值的神经网络，ELM 具有迅速收敛、不易存在局部极值等优点［24］，其原理为：

给定包含N个任意样本(xi，ti)的集合，其中xi= [xi1，xi2，…，xin] ∈Rn，ti= [ti1，ti2，…，tim] ∈Rm，输入层节点向量长度为n，输出层节点向量长度为m。

对于一个激励函数g(x)，且有K数量的隐藏节点的单隐藏层的神经网络，函数表达式为

式中：βi=[βi，1，βi，2，…，βi，n]T——输出节点与第i个隐藏层节点之间的一维权值向量；g(x)——激励函数（Sigmoid 函数、 Gaussian 函数等）；wi=[ωi，1，ωi，2，…，ωi，n]T——输入节点与第i个隐藏层节点之间的一维权值向量；bi——第i个隐藏层节点的偏置；(wi，xj)——wi和xj的内积；oj——样本的第j个维度输出值。

有监督学习的单隐层前馈神经网络的学习目标是使输出的均方误差最小，即存在βi，wi和bi使得

式中：tj——样本的第j个维度目标值；εj——样本的第j个维度目标值与输出值间的误差。

式（5）用矩阵表示为

式中：H——神经网络隐藏层的输出矩阵；β——输出权重矩阵；T——期望输出矩阵。

通常，期望找到估计值，和，对网络进行训练，达到有监督学习的目的，使得

这等价于求解最小化损失函数，即

传统的基于梯度下降算法的神经网络可以解决这类问题，但需要在迭代过程中不断调整参数。根据ELM 理论，输入权重值wi和隐藏层偏置bi被随机确定后，隐层的输出矩阵H就不会再变化，恒为常数矩阵。这时，ELM 的训练过程等效为求解Hβ=T的最小二乘解。理论上，如果训练样本数N无穷趋近于隐藏层节点数K，则矩阵H是方阵并且满秩。当输入权值和隐藏层偏置随机赋值时，ELM 可以零误差无限趋近于训练样本目标值，达到最理想状态。则Hβ=T的最小范数二乘解为

式中H╀——隐层输出矩阵H的Moore-Penrose 广义逆矩阵。

2 储层类型划分及识别

2.1 储层类型划分及测井响应特征

川中北部GM 地区是天然气的高产地带，其主力储集层震旦系灯影组沉积厚度大，分布范围较广，其中灯二段和灯四段均为良好的含气层系，是重要的油气勘探层系，根据取心及成像测井参考资料可知，灯影组二段可分为裂缝-孔洞型（Ⅰ类储层）、孔洞型（Ⅱ类储层）、裂缝-孔隙型（Ⅲ类储层）、及孔隙型（Ⅳ类储层）4 种类型（图1）。

图1 川中北部GM区块灯影组二段储层类型及测井成像特征Fig.1 Reservoir types and characteristics of imaging logging of Member 2 of Dengying Formation in GM block of north central Sichuan Basin

根据储层测井成像特征和岩心可以较准确地辨别储层类型，结合常规测井总结其特征：

Ⅰ类储层具有“两低两高”特征，即低深侧向电阻率（RLLD）、低自然伽马（qAPI），高声波时差（Δt）、高补偿中子孔隙度（ϕCNL），若存在一定的低角度或者斜角缝时，声波时差曲线会具有一定的周波跳跃现象［25］，深侧向电阻率分布为200～1 300 Ω · m；Ⅱ类储层具有“一低三高”的特征，低自然伽马，高深侧向电阻率、高声波时差、高补偿中子孔隙度，深侧向电阻率分布为800～2 000 Ω · m；Ⅲ、Ⅳ类储层则同时具备“三低一高”的特征，低声波时差、低补偿中子孔隙度、低自然伽马，高深侧向电阻率，深侧向电阻率分布为1 000～5 000 Ω · m。

2.2 储层类型识别及解释方法

根据储层测井响应特征可对其类型进行定性划分，但是受不同地层沉积环境及时期不同、岩性变化、含气饱和度等因素影响，其测井响应特征是不断变化的。为解决这一问题，在定性划分的基础上，提出一种基于滑动窗口的解释方法，具体实现过程如下（图2）：

图2 川中北部GM区块灯影组二段M9井滑窗计算过程Fig.2 Sliding window calculation process of Member 2 of Dengying Formation of Well M9 in GM block of north central Sichuan Basin

（1）以10 m 间距，结合成像测井图像及取心资料建立样本库，对于取心地层加密选点，保证每10 m 区域均覆盖样本；

（2）在该段地层的顶部建立一个50 m 滑动窗口H窗口1，获取该窗口区域中的储层类型样本数据及其对应的常规测井响应参数，通过对H窗口1中样本进行训练及预测，得到H窗口1区域储层类型解释数据；

（3）将该50 m 窗口按照10 m 步长进行下滑（深度统一增加10 m），进入第2 个50 m 滑动窗口H窗口2，获取该窗口区域中的储层类型样本数据以及其对应的常规测井响应参数，对H窗口2中样本进行训练及预测，得到H窗口2区域储层类型解释数据；

（4）将H窗口1与H窗口2重叠区域的储层类型数据进行算数平均计算，以此类推，一直计算到该段地层底部最后一个10 m 滑窗为止，期间建立的H窗口1、H窗口2、…、H窗口n覆盖整个地层。

将每相邻2 个滑动窗口重叠区域的数据进行算数平均计算，充分考虑了临近滑动窗口常规测井响应值变化的影响，包含了不断变化的沉积环境、岩性、含气水饱和度等。

针对上述这类计算量较大、精度要求高的算法，极限学习机不仅在计算速度上优于传统的支持向量机、BP 神经网络等，而且在对模型的拟合度上也优于逐步回归、多元线性回归等。需要注意的是，在选样过程中要避开因泥质或者井塌引起异常的井段。

2.3 斜率关联度计算

应用改进的斜率关联度算法对滑动窗口内样本及其深度对应的测井响应值进行计算分析，以GM区块灯影组二段M9 探井为例，根据第1 个滑动窗口H窗口1的测井响应数据（表1），计算其斜率关联度（表2）。

表1 川中北部GM区块灯影组二段M9井第1、第3滑动窗口测井响应数据（部分）Table 1 Logging response data of the first and third sliding windows of Member 2 of Dengying Formation of Well M9 in GM block of north central Sichuan Basin（partial）

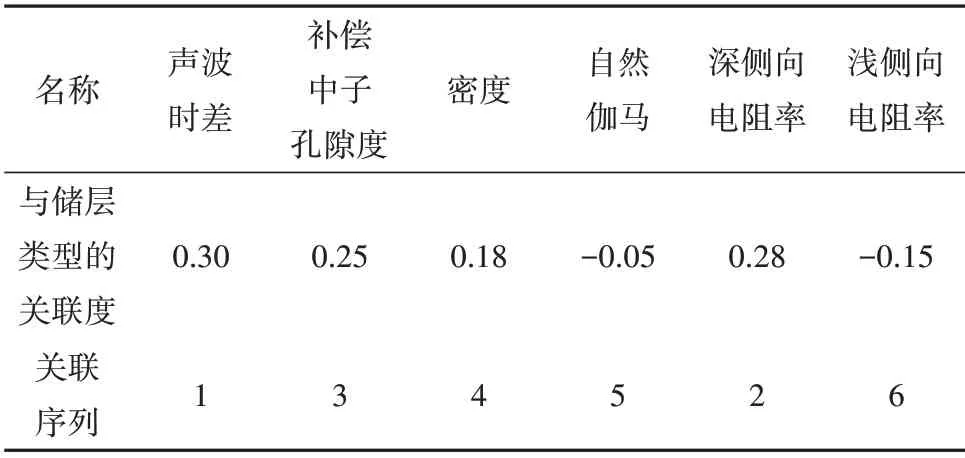
表2 川中北部GM区块灯影组二段M9井第1滑动窗口斜率关联度计算结果Table 2 Calculation results of slope coefficient correlation of the first sliding window of Member 2 of Dengying Formation of Well M9 in GM block of north central Sichuan Basin

通过表2可以得到4 条与储层类型正关联的常规测井曲线，关联度越高、关联序列越靠前，测井曲线对储层类型越敏感。其中排序第1 位为声波时差，第2 位为深侧向电阻率，第3 位为补偿中子孔隙度，第4 位为密度，因裂缝、孔洞的发育，三孔隙度曲线、深侧向电阻率曲线对储层类型响应明显，这一计算结果符合实际物理意义。在对M9 井第8 个滑动窗口H窗口8进行斜率关联度计算时，自然伽马曲线表现为正关联，通过完井报告、薄片鉴定等手段核实，该区段泥质含量较高，自然伽马响应明显，能得到牢靠的理论支撑。一些细微的变化如深、浅侧向电阻率受含气水饱和度等多种因素的影响，在小范围处理这些问题方面，机器学习有显著的优势，故在算法及程序设计上将关联度为正的测井曲线作为极限学习机的训练参数。

2.4 极限学习机参数优选

为使极限学习机建立的模型更具有效性及可靠性，对极限学习机激活函数选择、隐藏层节点个数进行研究。按照50 m 滑动窗口长度计算，单个滑动窗口中的样本数量集约为80 个，每个滑动窗口都是独立相似的单元，对单个滑动窗口进行实验能代表其余所有滑动窗口，选取M9 井第1 个滑动窗口H窗口1的80 个样本进行实验，训练集为包含不同类型储层的56 个样本，测试集（验证集）为包含不同类型储层的24 个样本。准确率验证公式为

式中：R——准确率，%；NTR——预测正确的样本数量；N——样本总数。

该实验利用Matlab 软件实现，测试结果表明：在准确度方面，当激活函数选为Sigmoid、Hardlim函数时优于选择其他函数；在稳定性方面，激活函数设置为Sigmoid 函数时，隐藏层节点个数为200～1 300 时准确率异常波动；从总体趋势可知，隐藏层节点个数设置越多，准确率越高（图3（a））；当隐藏层节点个数设置为2 613 个时，测试集准确率达到峰值95.54%（图3（b）），单次训练耗时小于0.01 s，能够满足储层类型划分的需求。

图3 极限学习机测试结果Fig.3 Test results of extreme learning machine

针对当隐藏层节点个数设置远大于样本数量时，正确率会出现有所波动的问题，采用在训练函数外嵌套一层while 循环，最大迭代次数设置为50，准确率达到95%则跳出循环，以保证准确率。

3 储层物性参数解释模型

对于川中北部GM 区块灯影组二段取心样本物性资料稀缺等问题，为准确解释储层的物性特征，需建立多种孔隙度解释模型对目标地层孔隙度进行定量解释；通过计算修正后的流动单元指数，应用离散岩石类型聚类技术划分孔渗等级，建立渗透率解释模型，实现对研究区储层孔隙度和渗透率的定量计算。

3.1 孔隙度解释模型

通过对相邻2 个滑动窗口储层类型叠加算数平均计算，既解决了地层变化因素对储层识别的影响，也降低了人工选样时存在的误差，先利用现有资料对研究区具有成像测井资料的6 口井进行储层类型识别，并获取425 个带有储层类型标签的孔隙度样本。基于本文划分的4 种不同的储层类型，利用斜率关联度对声波时差、密度、补偿中子孔隙度、自然伽马及深、浅侧向电阻率曲线进行优选，选取对孔隙度敏感的曲线，再通过极限学习机回归模式，按照本文的方式确定极限学习机参数，将分类后的孔隙度样本以7∶3 的方式用于ELM 训练与验证，分别建立4 种孔隙度解释模型，同时将采用ELM 回归算法的4 类孔隙度预测结果与采用PSO-SVM 算法得到的孔隙度预测结果进行比较。PSO-SVM 为采用粒子群优化算法的支持向量机［26］，其中决定系数（RDE）平均值为同种机器学习算法孔隙度解释模型RDE的算数平均值。

从表3可知，采用1 种孔隙度解释模型的PSO-SVM 算法的测试集RDE平均值分别为0.838 和0.831，而采用4 种孔隙度解释模型的ELM 算法效果更好，尤其是在对Ⅱ、Ⅲ、Ⅳ类储层的分类解释上精度更高，其中Ⅰ类储层孔隙度解释模型的测试集RDE较低，仅为0.735，通过多次岩心归位、测井数据标准化及ELM 参数调节均不能提高RDE，这应是由于Ⅰ类储层中“缝”的复杂特性，具体表现在裂缝的发育会使声波时差曲线出现一定的跳跃，裂缝的角度及张开度会引起深、浅测向电阻率的不同程度响应［27］，可尝试根据“缝”的种类再细分储层类型作进一步优化，但对取心及成像测井资料的要求更高。

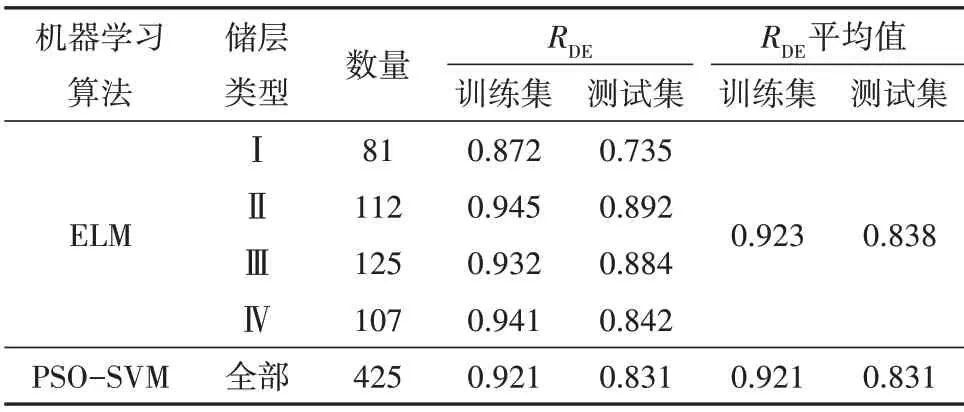
表3 不同机器学习模型的拟合性能比较结果Table 3 Comparison results of fitting performance of different machine learning models

3.2 渗透率解释模型

对研究区灯影组二段6 口井的104 个岩心实测孔隙度、渗透率数据进行交会分析，由于该区块储层的孔隙结构非常特殊且复杂，渗透率与孔隙度建立回归方程的拟合度R2仅有0.105（图4（a）），可见使用单一回归模型难以准确计算储层渗透率［28-29］。A.Mirzaei-paiaman 等［30］提出了一种修正的流动单元指数（FFZI*），得到计算渗透率的表达式为

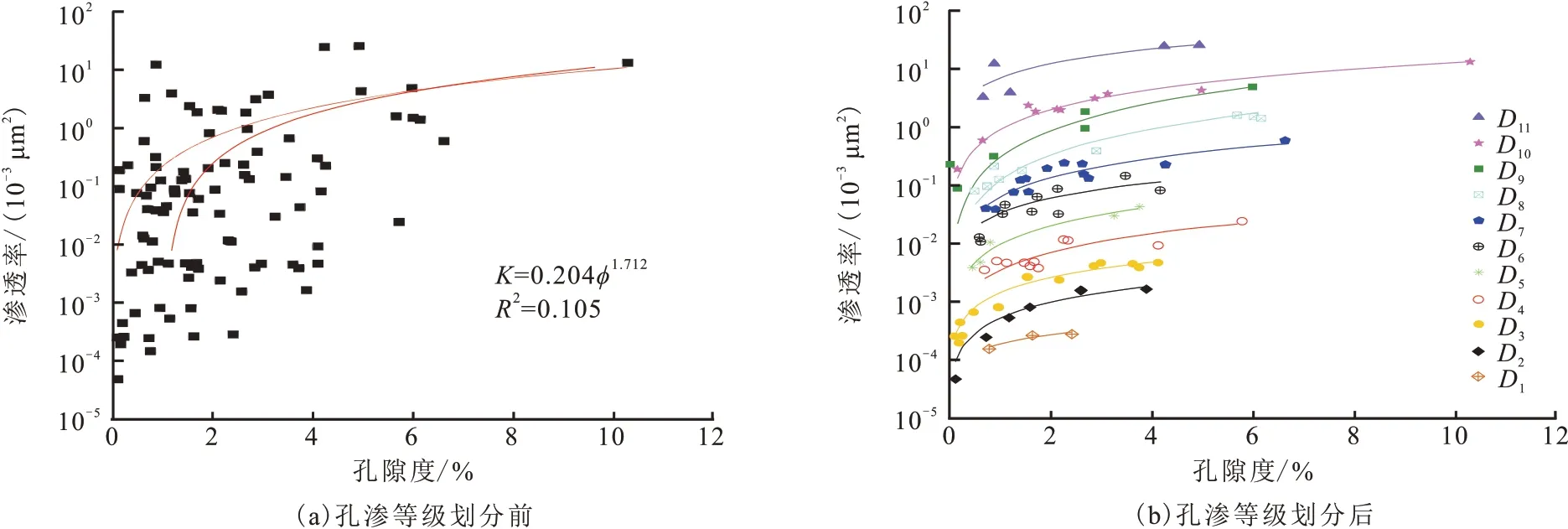
图4 川中北部GM区块灯影组灯二段储层取心分析孔隙度与渗透率关系Fig.4 Relationship between permeability and porosity of core analysis of Member 2 of Dengying Formation in GM block of north central Sichuan Basin

式中：K——渗透率，10-3μm2；ϕ——孔隙度，%；FFZI*——修正后的流动单元指数，μm。

Z.Zhang 等［26］研究认为将离散岩石类型（DRT）聚类技术与修正后的流动单元指数结合能提高渗透率的解释精度，其表征参数的表达式为

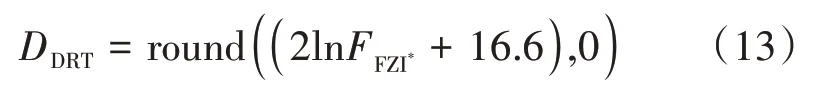
式中：DDRT——离散岩石类型表征参数；round（m1，m2）——取整函数，其中m1为待取整小数，m2为保留小数点后位数。

根据式（12）和式（13）可划分得到11 种离散岩石类型，将复杂的孔隙空间进行定量均匀划分（图4（b））。

不同的离散岩石类型反映总孔隙空间中溶蚀孔隙空间、裂缝孔隙空间及基质孔隙空间所占体积的不同。DRT 序列越高，表明总孔隙空间中裂缝孔隙、溶蚀孔隙越发育，同一总孔隙空间中因裂缝的发育，渗透率会增加几十倍，甚至近千倍。

通过斜率关联度、极限学习机回归模式建立了样本常规测井响应参数与FFZI*的解释模型，可对目标段储层FFZI*进行计算，根据式（13）计算得到相应的离散岩石类型表征参数，最后根据不同的离散岩石类型选用对应的孔隙度和渗透率关系的计算公式（表4），以实现对储层渗透率的定量高精度解释。

表4 孔隙度、渗透率关系的计算公式Table 4 Calculation formula of porosity and permeability

4 应用实例

利用本文提出的储层类型识别和解释方法及物性参数解释模型，对川中北部GM 区块M9 井灯影组二段储层进行常规测井综合评价。

如图5所示，M9 井在5 420～5 520 m 井段共计解释12 个气层，其中1、2、3、4、9、10、11、12 号气层在射孔井段内，5、6、7、8 号气层在射孔井段外。

图5 川中北部GM区块灯影组灯二段M9井5 420～5 520 m段的测井解释成果与产剖面对比Fig.5 Correlation between log interpretation and production profile of 5 420～5 520 m interval of Well M9 of Member 2 of Dengying Formation in GM block of north central Sichuan Basin

对比其测井综合解释及实际取心物性资料可知，本文方法建立的渗透率解释模型计算的结果与取心实测渗透率在数量级上一致，并且决定系数RDE高达0.81（渗透率取对数计算）；从叠加后储层类型成果可知，滑窗1、滑窗2 底部出现的零星Ⅰ类储层得到了很好的压制，充分融入了相邻地层变化的影响；对比2 号气层及10 号气层，2 号气层具有Ⅰ类储层及Ⅱ类储层共同发育特征；通过实际产气量对比可知，与孔洞型储层相比，裂缝-孔洞型储层对目标气层产能有更大贡献；12 号气层具有Ⅱ类储层及Ⅲ类储层共同发育特征，其中Ⅱ类储层及Ⅲ类储层具有近似的平均孔隙度，但渗透率却表现出Ⅲ类储层的明显高于Ⅱ类储层，最大值相差近20 倍，进一步分析可得出相同孔隙空间中裂缝对储层渗透率有显著的影响。

综上所述，Ⅰ类储层对研究区目标段产能有突出贡献，裂缝对储层渗流能力影响显著。本文研究的储层类型识别及解释方法和孔隙度、渗透率解释模型能够满足研究区目标地层的储层评价要求。