特低渗、致密油藏非线性渗流数值模拟方法及其在冀东油田的应用

李彦泽 段 彬 商 琳，2，3 孙彦春 龚丽荣 辛春彦 邢建鹏

（1.中国石油冀东油田公司，河北 唐山 063000；2.中国石油冀东油田公司博士后科研工作站，河北 唐山 063000；3.中国石油勘探开发研究院博士后流动站，北京 100083；4.中国石油大学（北京）安全与海洋工程学院，北京 102200）

0 引 言

油藏数值模拟技术自20世纪50年代诞生，到21世纪的今天已发展为一项较为成熟的常用技术，作为一种定量预测技术，具有精度高、三维可视化、能够直观揭示油气流在储层内的渗流过程等特点。在理论研究上，学者将其应用于探索多孔介质储层的复杂渗流问题；在油田开发中，数值模拟技术也广泛应用于开发方案、开发调整方案、油气藏提高采收率方案等，为油田开发技术政策的制定提供了重要支撑［1-6］。目前，Eclipse、CMG、VIP 等是目前应用比较广泛的商业数值模拟软件，都以达西渗流模型为核心，在中高渗透油藏中成熟应用。流体在特低渗透、致密砂岩等多孔介质储层中的流动，由于边界效益表现为存在最小启动压力梯度的低速非线性渗流，达西线性渗流难以表征此类储层中流体的渗流过程［7-9］。因此，目前市面上常用的商业数值模拟软件在特低渗透、致密砂岩油藏数值模拟中应用误差相对增大。

自20世纪90年代以来，众多学者开展了低渗透、致密砂岩储层非线性渗流规律研究，也探索了相应的数值模拟方法［10-16］，主要认识有3 个方面：一是普遍认识到流体在特低渗透、致密砂岩等多孔介质储层中的流动，存在最小启动压力梯度，且为低速非达西渗流，达西渗流模型在一定程度上夸大了储层的渗流能力；二是部分学者提出的拟启动压力梯度模型，不能表征低速非线性渗流阶段，表现出储层渗流阻力增大，造成采用拟启动压力梯度模型的数值模拟软件的预测结果误差较大；三是部分学者提出变渗透率的数值模拟方法，该方法可以准确地描述特低渗透、致密储层多孔介质的非达西渗流，但未能给出连续光滑的渗透率状态方程，而且现有的变渗透率数值模拟软件没有能够给出压力梯度场和渗透率场的变化规律，因此变渗透率数值模拟方法未得到很好地应用。

为解决非线性渗流模拟问题，通过理论模型推导，建立非线性渗流模型，并求解非线性渗流系数。鉴于tNavigator 中的启动压力梯度限制为定值，无法体现非线性渗流规律，本文研究考虑对渗透率进行时变，即通过对渗透率进行修正来反映启动压力梯度的变化，从而反映非线性渗流。现有软件无法实现压力梯度的网格表征，通过前期网格筛选，在定压条件下进行模拟。

1 非线性渗流模型构建

原油成分极其复杂，并不是单纯的牛顿流体，其存在屈服应力，而孔喉的微小使得原油的非牛顿性质更强，不可以忽略。以经典的毛管模型为例，流体匀速通过毛管时力学平衡关系式为

式中：Δp——毛管两端的驱动压差，MPa；

r——毛管半径，μm；

τ0——流体屈服应力，MPa；

μ——流体黏度，mPa·s；

v——流体渗流速度，cm/s；

L——毛管长度，μm。

Δpπr2是驱动力，是内摩擦力，τ0体现出流体的非牛顿性对流体渗流的影响计算公式为

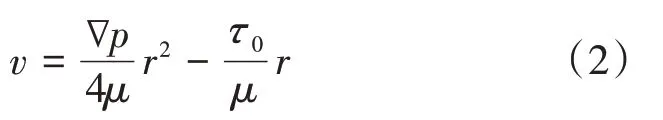
式中 ∇p——驱动压力梯度，MPa/m。

原油中的极性成分在渗流通道固相表面的吸附，导致边界层的存在是必然的。从前述实验可知，低渗透油藏孔喉细微，比表面大，边界层的影响是不可以忽略的，考虑边界层后流量的计算公式为

式中：q——单根毛细管流量，cm3；

δ——边界层厚度，μm。

δ体现出固体与液体分子、液体与液体分子之间相互作用对流体渗流的影响；油藏岩心相当于一组半径均为r的平行毛细管埋置于固体之中。如果与流动方向相垂直的每单位横截面面积上有N根这样的毛细管，则通过该多孔介质块的流量计算公式为［17-18］

式中：Q——截面流量，cm3；

K——渗透率，10-3μm2；

A——截面积，cm2。

式（4）相对于达西定律更符合实际情况，但形式太过复杂，多位学者研究了边界流体对低渗透、致密储层渗流规律的影响，认为边界层厚度随驱动压力梯度的增大而减小。龙腾［15］测定了去离子水通过微管的流量与驱替压力梯度之间的关系，并计算出去离子水在微管中边界层厚度随驱替压力梯度的变化曲线。闫庆来等［5］指出随着驱替压力梯度的增大，边界层流体厚度呈指数减薄，说明边界层厚度是驱替压力梯度的函数。理论与实验证实驱替压力梯度越大，储层的边界层越薄。由前述边界层实验有边界层比例与压力梯度呈幂函数关系，与黏度呈线性关系，对于单根毛细管，有

式中a，b——拟合系数，常量。

式（5）非线性化较高，对于后面模型推广与实用较差，因此，通过进一步结合实验数据，对于压力梯度采用反比例函数表示，即

由边界层厚度定量表征可知，在压力梯度过大时，边界层比例减少较小，趋于稳定，并不完全符合整体函数关系，去除掉压力梯度过大后的点所得到的2 种表征方式系数与误差如表1所示，转换为反比例函数后误差为15.17%，相对于幂函数关系12.77%的误差，误差增加不大，且可极大减小模型复杂程度。因此，在后续推导过程中使用简化过后的边界层厚度定量表征公式。

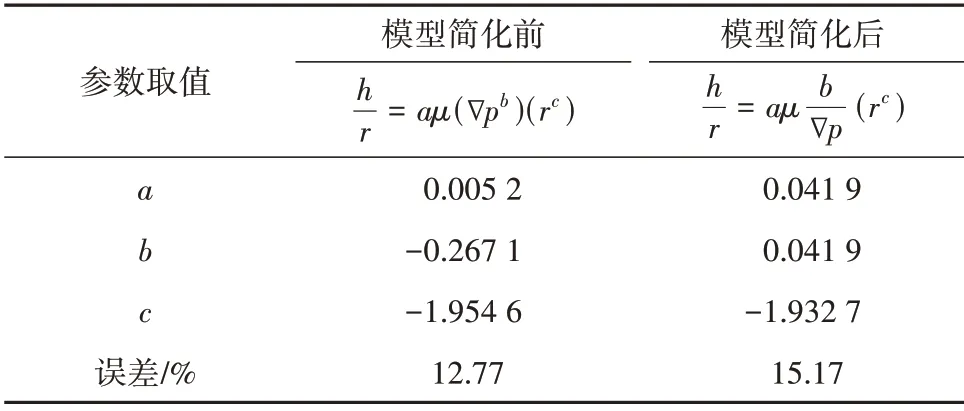
表1 边界层公式简化前后误差对比Table 1 Error comparison of boundary layer formula before and after simplification

忽略高阶无穷小项后，有

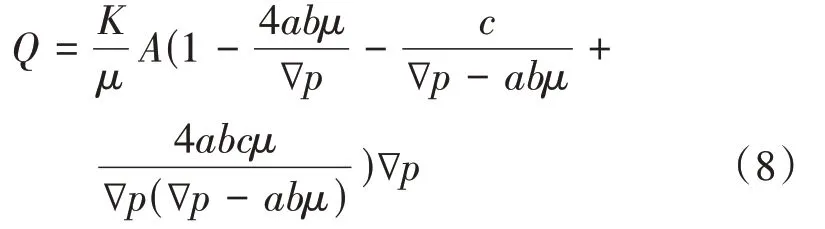
最终有

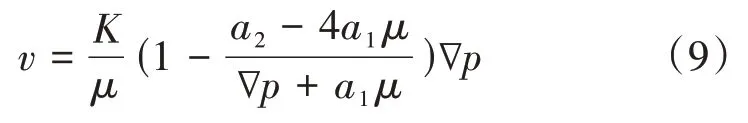
2 非线性渗流数值模拟方法

外部软件计算模型拟合参数，非线性渗流模型里的a1、a2两个参数，对于不同类型储层，值均不同，通过现有的岩心数据，利用matlab 进行非线性拟合。通过对研究区块进行全面、系统、综合研究，应用油气勘探、开发过程中获取的地震、测井、测试、钻井以及开发动态等资料，建立更加贴近于客观沉积演化规律的精细化三维地质模型。对油藏储层进行精细描述和预测，为非线性渗流模拟提供可靠的地质依据。对于采用的非线性渗流模拟方法，渗透率场和压力场有直接影响，防止场数据的极值化，将渗透率场与压力场初始化。对于井周网格进行平面方向的逐个筛选，并将其赋值，便于直接调用。将建立的非线性渗流模型通过渗透率时变的方式导入，输出考虑非线性渗流的模拟结果，并与其他模型比较。导入历史数据，通过不同算法对模拟结果进行智能历史拟合，反馈数据，调整非线性渗流参数（图1）。

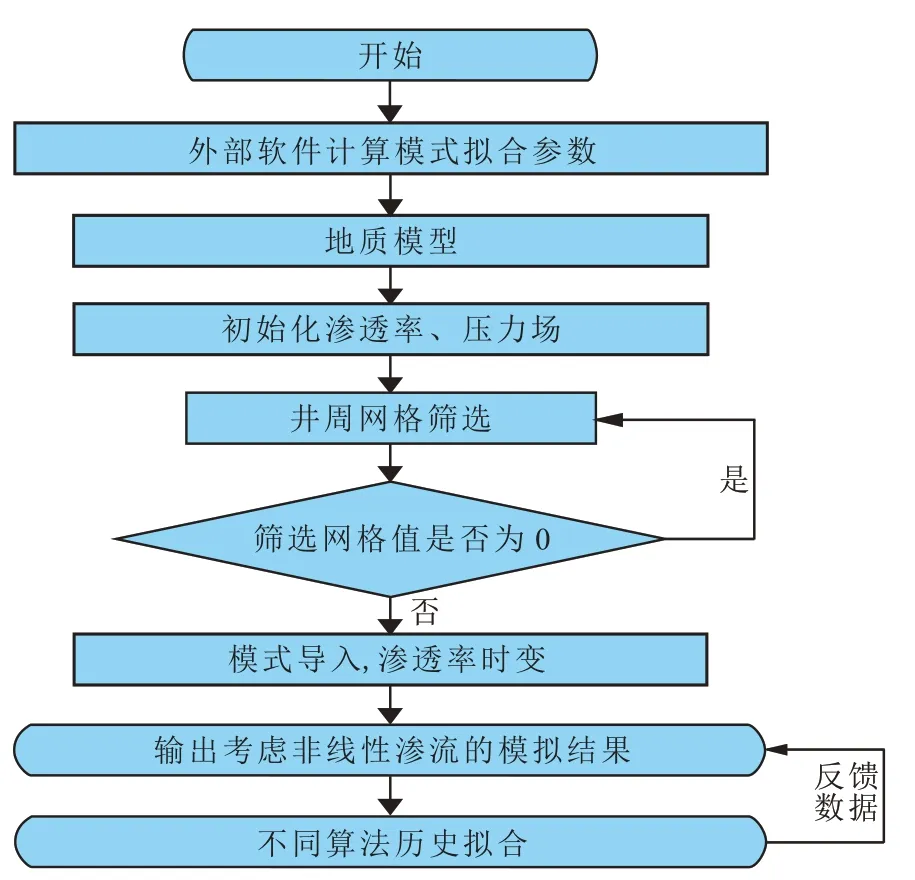
图1 致密砂岩油藏非线性渗流模拟流程Fig.1 Workflow of nonlinear flow simulation in tight sandstone reservoir

3 应用实例

3.1 模拟流程

由于现场压力梯度测量较为困难，因此根据实验室已开展的岩心驱替实验数据进行非线性渗流参数的拟合，根据储层分类结果，选取冀东油田南堡403X1 断块典型井组进行计算，并选取渗透率在1×10-3～3×10-3μm2内的岩心数据进行非线性拟合。南堡403X1 断块Ed2储层为一套辫状河三角洲前缘砂体沉积，储层平均渗透率为2.8×10-3μm2，属典型的特低渗油藏和层状构造岩性油藏，采用压裂注水开发技术进行开发，经过近10 a 滚动开发，已经进入高含水阶段，注入水沿人工裂缝窜流严重，剩余油分布复杂，急需探索剩余油分布规律，为开发调整提供依据。结合钻井资料、物性参数、生产动态等资料对M 区块进行属性建模，平均渗透率为1.29×10-3μm2，平均孔隙度为11.66%，平均深度为3 324.2 m，含油饱和度为46.2%，含水饱和度为53.8%。

3.1.1 初始化场图

根据推导的非线性渗流模型，在采取渗透率时变的过程中，时变的渗透率是每一个时间步在上一个时间步的基础上进行倍乘，不加以控制会导致渗透率无限倍乘出现极值，需对其进行初始化，防止极值情况出现。利用渗透率场初始化、压力场初始化模型（图2），使每步调用初始渗透率参与时变计算。

图2 初始化模型Fig.2 Initialization model

3.1.2 井周网格筛选

tNavigator 无法做到压力梯度的表征，因此根据泄油半径距离，通过筛选网格的方式进行压力梯度的模拟，通过Voronoi 图指定半径的方式进行网格筛选。可将井周范围内的网格进行筛选，便于之后对压力梯度进行表征。以网格长度为最小单位步长进行筛选（图3）。

图3 井周网格筛选Fig.3 Grid screening around the well

将井附近网格筛选过后，对于井周围不同距离的网格可近似表示压力梯度。

3.1.3 渗透率时变

tNavigator 中的启动压力梯度限制为定值，无法体现非线性渗流规律，采用对渗透率进行时变的方法，即通过对渗透率进行修正来反映启动压力梯度的变化，从而反映非线性渗流。对于井周不同距离的网格进行非线性渗流模型的导入，改变渗透率，在井底流压大于0 MPa 的情况下，将推导的非线性渗流模型导入，结合实际生产情况，对井周不同范围内的网格进行渗透率时变。

3.2 结果分析

历史拟合情况及对比，对导入考虑非线性渗流影响的模型作智能历史拟合，采用拉丁超立方实验算法对日产油量、累计产油量进行拟合（图4、图5），选取拟合程度较高且参数均科学合理的拟合模型，并与现有的拟启动压力梯度模型进行比较。

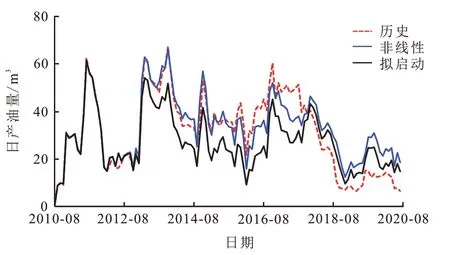
图4 不同模型日产油量对比Fig.4 Comparison of daily oil production of different models

图5 不同模型累计产油量对比Fig.5 Comparison of cumulative oil production of different models

模拟结果表明，考虑非线性渗流的模型，模拟日产油量与实际产油量相关性、趋势性较好。累计产油量由非线性模型拟合结果为12.085 9×104m3，与实际产油量11.424 8×104m3相比，误差为5.47%，拟启动模型产油量为9.826 8×104m3，误差为13.99%。由此不难发现，非线性模型拟合日产油量和累计产油量与实际生产情况更接近，符合率更高，由此表明该方法适用于特低渗、致密砂岩油藏数值模拟。

4 结 论

（1）基于非线性渗流理论及启动压力实验、边界层实验，推导了不同类型储层的非线性渗流新模型，综合考虑了启动压力梯度、边界层厚度对非线性渗流的影响，新模型考虑了流体黏度的影响。

（2）基于非线性渗流模型，开展商业软件二次开发，通过筛选井周网格及对渗透率场与压力场初始化，结合实验数据，对渗透率进行时变反映非线性渗流对储层的影响，形成了非线性渗流数值模拟方法。

（3）利用本文方法对典型井组历史拟合，通过对比来看拟启动压力梯度模拟方法夸大了地层阻力，数值模拟结果低于实际产量，非线性渗流模型更符合实际生产情况，误差更小，由此证明该方法适用于特低渗致密砂岩油藏数值模拟。