回收钢纤维对超高性能混凝土和易性和力学性能的影响
2022-12-02南雪丽姬建瑞陈广钊唐维斌
南雪丽,陈 浩,姬建瑞,王 毅,陈广钊,李 梅,唐维斌
(1.兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室,兰州 730050; 2.兰州理工大学 材料科学与工程学院,兰州 730050; 3.甘肃省交通规划勘察设计院股份有限公司 高性能材料研究所,兰州 730000)
1 研究背景
超高性能混凝土 (Ultra-High Performance Concrete,简称“UHPC”)是一种新型水泥基复合材料。UHPC具有超高强度、高韧性及优异耐久性等特点,抗压强度一般在120 MPa以上,是传统普通混凝土的3倍以上[1-2],但其基体脆性极大,易在较低应变水平下发生破裂[3]。掺入工业钢纤维是克服此问题的最有效途径,已在工程混凝土生产中被广泛采用,但工业钢纤维在生产过程中消耗大量自然资源,并且由于CO2排放而严重影响自然环境,研究人员为寻求一种可持续和有效的替代高价工业钢纤维的方法已经进行了大量研究工作[4]。近15 a以来,在废旧轮胎中提取的回收钢纤维(Recycled Steel Fiber,简称“RSF”)被发现是工业钢纤维(Industrial Steel Fiber,简称“SF”)的最佳替代品,具有有限的环境影响和较低的回收成本[5]。
目前国内外学者针对SF对UHPC力学性能的影响进行了大量研究。Abbas等[6]采用不同钢纤维掺量及长度,研究其对UHPC力学性能的影响,结果表明随着纤维掺量的增大,抗压强度略有增大,但钢纤维长度对抗压强度和耐久性无明显影响。Yang等[7]采用5种类型钢纤维掺入UHPC中研究其对UHPC力学性能的影响,结果表明相比于SF,RSF的掺入对抗压强度的损失较少,损失率仅为2.5%。这些研究工作表明SF的掺入可以改善UHPC的力学性能,有关RSF对UHPC和易性和力学性能的影响研究以及2种钢纤维之间的比较研究较少。本文通过在UHPC中掺入SF和RSF分别制备出SFUHPC和RSFUHPC,采用流动度、流变参数、新拌及硬化后的纤维分布、抗压强度、抗折强度等性能指标,研究2种不同类型钢纤维对UHPC和易性和力学性能的影响,分析RSF替代SF的可行性,为进一步推广RSF在UHPC中的应用及UHPC的配合比设计提供依据。
2 原材料与试验方法
2.1 原材料
本研究中水泥为P·O 42.5普通硅酸盐水泥,矿物掺合料为1级粉煤灰和硅灰。主要化学成分如表1所示。选取长径比为50~70的直钩形回收钢纤维进行试验,其技术指标及化学成分分别如表2、表3所示。原材料的微观形貌如图1所示。减水剂为聚羧酸系高效减水剂,减水率为30%。所用砂为石英砂,控制20~40目、40~70目和70~120目质量比为1∶1.04∶0.85。SF和RSF实物如图2所示。SF(图2(a))采用工业镀铜钢纤维,RSF(图2(b))采用废旧轮胎经过回收加工厂机械破碎及电磁筛分后的废旧钢纤维。

图1 原材料SEM图像

图2 两种钢纤维图片及SEM图像

表1 原材料的主要化学成分

表2 钢纤维性能参数

表3 钢纤维化学成分
2.2 配合比设计
本试验采用可压缩堆积模型(CPM)进行配合比设计计算。UHPC含有较多组分的超细颗粒,CPM模型是建立粉体超细颗粒的最紧密堆积模型,共有3种交互模式,无交互和完全交互是两种极限的交互,无交互是某级颗粒间的堆积过程不受其他粒径存在的影响,完全交互是指不同级颗粒间完全交互[8]。实际堆积过程是大颗粒与小颗粒部分交互影响,小颗粒嵌入到大颗粒中的过程,小颗粒会影响大颗粒本身的堆积,产生“松动效应”,此时大颗粒占主导位置;当小颗粒占主导位置时,大颗粒会影响到小颗粒堆积,产生“壁面效应”[9]。为把实际情况转变为以上的2种极限情况以便于计算,根据三元混合料堆积过程推导出松开效应系数和壁效应系数。然后经过引入反应不同粒径颗粒占主导地位时压实程度的压实指数K,经推导得到K与密实度的表达式(1),最后代入各个原料的占比求解方程即可得到UHPC的实际堆积密实度[8]
(1)
式中:K为压实指数;Φ为混合料体系实际堆积密实度;γi为混合料体系中第i粒级颗粒的虚拟堆积密实度;βi为混合料体系中第i粒级颗粒剩余堆积密实度。利用颗粒堆积模型可以提高UHPC中超细颗粒的堆积密实度,进而提高UHPC颗粒结构致密性,减少混凝土颗粒堆积空隙体积[10]。
2.3 试件制备与养护
根据CPM模型计算得出各试验组配合比如表4所示。制备时,先将水泥、粉煤灰、硅灰和石英砂放入搅拌机中干拌1 min,形成干混料,再将减水剂及水加入干混料中先慢搅5 min,再快搅1 min形成匀质浆体,最后加入钢纤维慢搅2 min。搅拌结束后,立即进行流动度及流变性能测试,测试完成后成型于100 mm×100 mm×100 mm及100 mm×100 mm×400 mm的模具中,24 h后脱模放入水中养护至力学性能测试龄期。

表4 UHPC试验配合比
2.4 试验方法
2.4.1 和易性试验
由于UHPC中没有掺加粗骨料,故流动性试验根据《水泥胶砂流动度测定方法》(GB/T 2419—2005)进行。流变试验采用HAKKE Viscotester iQ流变仪对UHPC基体胶凝材料浆体的流变性能进行测试,测试容器为体积500 mL、直径85 mm、高130 mm的圆筒罐,测试程序参照Viktor Mechtcherine[11]的试验方法,即连续剪切速率控制试验。
钢纤维分散度测定试验分为新拌UHPC钢纤维分散度测试和硬化UHPC钢纤维分散度测试。其中新拌UHPC钢纤维分散度测试采用磁吸法,其测试方法为:UHPC搅拌均匀后,按照顺序倒出均匀分为四等份,将每份UHPC用水冲洗同时用磁铁吸取每份中的钢纤维,再将提取出的钢纤维进行烘干分离及称重。根据小林一辅[12]提出的纤维在水泥基材料中的分散度理论,本试验采用分散度λ衡量纤维在UHPC中的分散情况,如式(2)、式(3)所示。
亳文化的译介主体是多元的,有亳州市政府部门如宣传部、新闻办、文化旅游局、旅游公司、景区管理部门,以及译员、审校员等。在亳文化译介中,亳州市政府部门应发挥主导作用,市宣传部、新闻办等联合文化旅游局制定相应的标准和政策来规范亳文化的译介。旅游公司、景区管理部门等应积极参与亳文化的译介与传播活动,提高工作人员的宣介意识与能力。译员和校对人员应提高理论水平与译介能力,增强责任与担当意识,严把译文质量关,使得亳文化的内涵准确、有效地传递给国外受众。
λ=e-φ(x),
(2)
(3)
式中:xi为试样中钢纤维含量;μ′为等分试样中钢纤维含量的平均值;n为等分试样的个数。当全部纤维集中在同一等份中,其他等份纤维含量为0时,λ=0;当钢纤维完全均匀分布在每个等份中时,λ=1,故λ应在0~1之间取值,且分散度的结果越接近1,钢纤维分散越均匀。
UHPC硬化后进行硬化UHPC钢纤维分散度测试,首先对UHPC进行切割,然后拍照采集截面图像,利用PS软件进行二值化处理并划分区域,最后对截面钢纤维进行统计,运用式(2)、式(3)计算其分散程度。
2.4.2 力学性能试验
根据规范《水泥胶砂强度检验方法(ISO 法)》(GB/T 17671—1999)和《建筑砂浆基本性能试验方法标准》(JGJ/T 70—2009)进行力学性能测试。
3 结果与分析
3.1 钢纤维掺量与类型对UHPC流动度的影响
各类型UHPC流动度如图3所示。由图3可知,随着2种钢纤维掺量的增加,UHPC流动度均降低,这主要是因为UHPC中加入钢纤维后,原附着在细骨料上的水泥浆体量下降,导致UHPC流动度下降。由图4所示,对于2种钢纤维,在掺量低于1.0%时,流动度损失率均低于10%,这是由于钢纤维产量过少,不会对UHPC的紧密堆积结构产生影响,故流动度降低不大[13]。当钢纤维掺量从1.0%增大到2.0%时,UHPC的流动度损失率增大20%左右,这主要是钢纤维大量掺入导致UHPC的紧密堆积结构破坏,并对其基体产生极大束缚,并使骨料周围的水泥浆体减少,导致流动度下降。

图3 钢纤维掺量对UHPC流动度的影响

图4 钢纤维掺量对UHPC流动度损失率的影响
从图4中还可知,当钢纤维掺量增大到1.0%以上时,RSFUHPC流动度损失率明显大于SFUHPC,这是因为相对于SF,RSF的长度和形状极不均匀,且表面粗糙,如图2所示,对UHPC基体的粘结能力更强,随着纤维掺量的增加,RSF对基体的束缚作用愈发明显,进而导致UHPC流动度损失率增大。
针对影响UHPC流动度的2个因素——钢纤维类型及钢纤维掺量进行统计性试验方差分析,运算得到P值(P-value)。P-value表示的是试验因素对试验结果无显著影响的概率[14]。当P-value≤0.01时,说明因素对试验结果的影响非常显著(**);当0.01

表5 影响流动度因素的显著性分析
3.2 钢纤维类型对UHPC屈服应力及塑性黏度的影响

图5 通过修正的宾汉姆模型拟合得到的剪切应力与剪切速率曲线

(4)

回归方程与流变学参数的结果如表6所示。屈服应力和塑性黏度是衡量新拌混凝土流变性能的重要参数,屈服应力主要是由于浆体内各颗粒之间的附着力与摩擦力产生的,主要受水泥基胶凝材料的各颗粒间距、粒径尺寸和电位电势的影响,是引起材料流动变形的最小剪切应力。因此屈服应力越小,水泥浆体越容易发生流动。塑性黏度是指材料内部结构阻碍浆体流动的性能,它受颗粒形状、颗粒大小和颗粒浓度等的影响,反映胶凝材料浆体体系变形的速度,塑性黏度小,相同外力作用下浆体流速大。但塑性黏度过小,会导致新拌水泥基复合材料浆体发生离析[17]。不同掺量及类型钢纤维掺入UHPC对屈服应力和塑性黏度的影响如图6所示,由图6可知,无论加入何种类型钢纤维,都会使得UHPC体系中各颗粒之间的摩擦力增强,导致UHPC的屈服应力明显增大。其中RSFUHPC的屈服应力及塑性黏度均大于SFUHPC,主要是由于钢纤维在拌合物中的棚架作用能够阻碍拌合物的流动,RSF的长径比不均匀,导致棚架效应越明显,流动阻力就会越大。c/μ值均>0,呈现出剪切增稠的现象,其中c/μ(RSFUHPC) 表6 回归方程与流变学参数的结果 图6 不同钢纤维种类及掺量对UHPC屈服应力及塑性黏度的影响 新拌UHPC钢纤维的分散度运用磁吸法进行提取计算,对钢纤维掺量为1.0%和2.0%的UHPC进行提取并对所得钢纤维进行称量计算分散度。硬化后的UHPC通过统计截面钢纤维数量进行钢纤维分散度计算,其二值化图像如图7所示。2种钢纤维分散度的计算结果如表7所示。由表7可知,RSFUHPC的分散度在新拌及硬化状态均大于SFUHPC,这是由于SF表面光滑且直径较小,并且UHPC中运用大量高性能减水剂使其凝结时间相对延长,从而导致在拌合后SF由重力原因产生沉降,使硬化后的SFUHPC截面钢纤维分散极不均匀,图7中可以看出,SF聚集在下表面或骨料周围,在实际工程中有不均匀破坏的风险。而RSF由于其长度及直径参差不齐,且在其周围粘结有橡胶颗粒(见图2),掺入后对新拌UHPC浆体有较强的约束作用,棚架效应更加明显,故RSF有更强的分散效果。 图7 硬化UHPC截面中钢纤维二值化图像 表7 钢纤维分散度 图8为钢纤维掺量对UHPC抗折强度的影响,由图8可知在三点抗折试验中,随着2种钢纤维掺量的增加,抗折强度增大。由图9可知,破坏荷载峰值逐渐升高,且在达到破坏荷载后,由于纤维含量的增加,后续曲线变得更加曲折且变化值更大,这主要源于掺入钢纤维后,在抗折试验中达到破坏荷载后,继续加载,其中的钢纤维会逐根拔出,导致后续曲线更加曲折且位移更大[18]。 图8 钢纤维掺量对UHPC抗折强度的影响 图9 UHPC荷载-位移曲线 通过三点抗折试验,记录荷载-位移曲线。该曲线下面积越大,表明材料破坏过程中能够吸收的能量越多,材料抵抗断裂的性能越好[19]。因此,荷载-位移曲线下的面积可较好地表征材料的整体韧性。 如图10所示,随着2种钢纤维掺量的增加,位移-荷载曲线下的面积逐渐增大,说明掺加钢纤维可以显著提高UHPC断裂时的断裂能。其中SFUHPC的位移-荷载曲线下的面积相对于RSFUHPC更大,更难进行断裂,这是因为RSF长度及直径不一,分散度大,且RSF表面橡胶粘附较多,RSF与UHPC基体连接不密实,UHPC断裂时,一部分RSF由于表面橡胶颗粒的作用更易拔出,从而导致位移-荷载曲线下面积变小,断裂能随之变小[20]。但由表8及表9可知,经过方差分析,P-value(钢纤维类型)分别为0.14和0.15,均>0.05,钢纤维类型不同对UHPC抗弯荷载—位移曲线下面积及抗折强度的影响不显著,故RSF可以替代SF掺入UHPC,且不影响抗断裂效果。 图10 钢纤维掺量对UHPC荷载-位移曲线下的面积的影响 表8 影响抗折强度因素的显著性分析 表9 影响荷载-位移曲线下面积因素的显著性分析 不同类型及掺量的钢纤维对UHPC抗压强度的影响如图11所示。相同掺量下,两种类型钢纤维对UHPC抗压强度几乎没有影响。当钢纤维掺量由0%增大到2.0%时,RSFUHPC抗压强度从129 MPa增大到148 MPa,SFUHPC抗压强度从129 MPa增大到149 MPa,两者钢纤维28 d抗压强度只差1 MPa,且钢纤维掺量从0%增大到2.0%时,抗压强度只增加20 MPa左右,变化不明显。这是由于试件在受到竖向荷载作用时会发生横向变形,掺入钢纤维后,依靠纤维与水泥基体之间的黏结作用,内部的纤维能够起到一定的限制横向膨胀的作用[21-23]。因为纤维在基体中乱向分布,其体积掺量较小(1.0%~1.5%)时,会在基体中形成相对均匀的网络搭接结构,随着掺量的增加会对基体产生更大约束力,从而提高抗压强度[24]。然而,由于钢纤维乱向分布,在限制横向变形时,仅有部分纤维发挥作用,所以纤维掺量的增加对材料的抗压强度提高较小,且两种类型的钢纤维变化趋势相同。 图11 钢纤维掺量对UHPC抗压强度的影响 (1)当钢纤维掺量在1%及以下时,随钢纤维掺量的增加,RSFUHPC与SFUHPC流动度损失率均<10%,当掺量增加到2.0%时,RSFUHPC流动度损失率超出SFUHPC 4.44%。但经过统计学显著性分析,钢纤维类型对UHPC流动性的影响并不显著。 (2)RSFUHPC的屈服应力及塑性黏度均大于SFUHPC,但RSFUHPC的剪切增稠程度(c/μ)较SFUHPC有所降低,表明掺入RSF可以改善UHPC在泵送过程中出现的离析、泌水等现象。 (3)当钢纤维掺量一定时,RSF在新拌及硬化UHPC中的分散度(0<β<1)比SF高出0.1左右。故在实际工程中掺入RSF可以降低UHPC的施工难度,增强新拌UHPC匀质效果。 (4)当钢纤维掺量一定时,RSFUHPC的抗折强度、荷载-位移曲线下面积及抗压强度均小于SFUHPC,但经过统计学显著分析,P-value均>0.05,钢纤维类型对其力学性能影响不显著,且28 d抗压强度仅相差1MPa。 (5)综上相对于SF,RSF的掺入对UHPC的流动性及力学性能没有显著影响,并可以使纤维分散度提高,剪切增稠程度降低,实际工程施工难度及成本降低,故RSF可以替代SF运用于UHPC中。

3.3 钢纤维类型对新拌及硬化UHPC分散度的影响


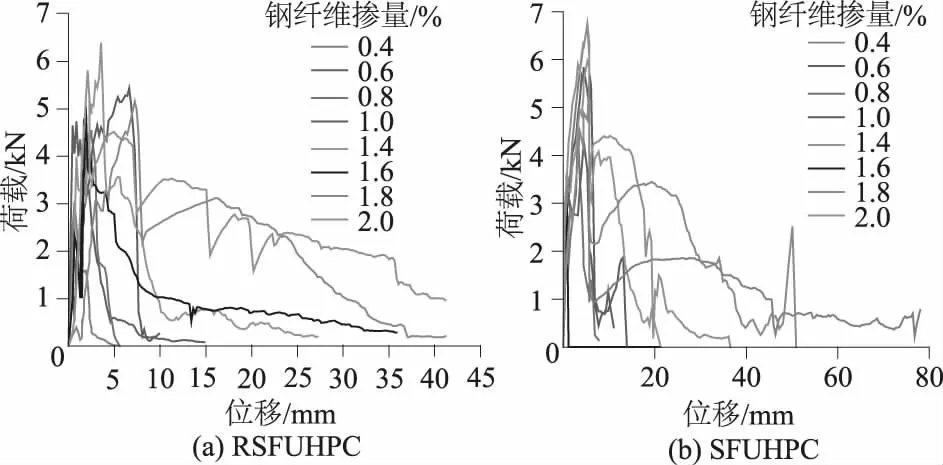
3.4 钢纤维类型对UHPC荷载-位移曲线的影响



3.5 钢纤维掺量及类型对UHPC抗压强度的影响

4 结 论
