二级边坡织物袋挡墙的侧向承载特性研究

关晓迪，秦泽轩,2*

(1.西安理工大学岩土工程研究所，陕西 西安 710048;2.河南安钢泽众冶金设计有限责任公司，河南 郑州 450003)

织物袋作为生态环保型护坡材料，具有抗老化、抗紫外线、无毒、不降解、百分之百可回收的特点，它的孔径可提高过滤作用以防止土体颗粒进入产生淤堵[1]。织物袋在国外应用较广，在公路、铁路边坡防护，湖岸和河岸砌护，水库迎水坡防冲等领域均有涉及[2-8]；在国内，其主要应用于公路、铁路、水利工程及环保工程建设，引水渠的防渗等，但还处在探索阶段，因此，对边坡支护的理论研究及工程建设均具有十分重要的意义。

目前，许多学者通过现场试验、模型试验和数值模拟，对织物袋支护的边坡变形及破坏进行了大量的研究[9]。王伟等[10]介绍了土工织物袋充填沙筑堤施工工艺和方法，总结了其相关工程经验和控制措施以期为实际工程服务。梁静等[11]通过定水头冲刷模型试验，对冲刷前后土工织物的物理力学参数进行对比分析，发现采用拉伸强度作为材料抗冲刷性能较为合理。高霞等[12]通过分析陕西秦巴山区织物袋筑坎梯田田坎坎高、坎坡与稳定性之间的关系，明晰了田坎坡度越大，适宜的坎高越低，反之则越高的规律。Plaut等[13]考虑土工袋在完成充填后，袋内土体会产生上下分层现象，同时考虑摩擦效应对土工袋袋体的影响。王艳巧等[14]通过模型试验，对细砂、粗砂和壤土3种填料的土工袋进行激振试验，发现土工袋是一种很好的减震构造且与袋内填料关系不大，且研究了减震效果受土工袋的层数与排列方式的影响。Tantono[15]通过对袋体与填料不同的接触关系进行了数值模拟，分析了竖向应力作用下土工袋的承载特性。李卓等[16]通过开展土工袋和土在冻融循环作用下的模型试验，发现了土工袋的冻胀量和融沉量均小于土冻胀量和融沉量，证明了土工袋可以有效地防止结构冻融、冻胀破坏。邱长林等[17]发现粉土在砂袋填充过程中形成重度不均匀的泥浆，根据不均匀重度对土工袋填充形状及力学特性的影响，建立了土工袋的变形方程，并利用数值方法进行验证。刘斯宏等[18]通过对土工袋的循环剪切试验，得到其应力应变滞回圈，依据等效阻尼比远大于钢筋混凝土结构得出土工袋减震效果良好。郑建壮等[19]运用土工袋填土围堰技术，治理钱塘江河口海塘工程，从其结构与布置、施工方法、经济指标等方面证明土工袋的可行性。黄小元[20]提出土工格栅包裹土工袋复合加筋结构，通过单轴压缩试验、模型试验和数值分析探讨其承载性能和工程应用，证明返包土工袋加筋挡土墙支护效果远大于传统土工袋挡土墙，并且可以抑制墙后土体的破坏变形。郑斌[21]提出了一种连接式土工袋挡土墙，通过设计模型试验，对试验数据进行分析，研究了连接式土工袋挡土墙的破坏形态，并运用三维土工袋加固机理进行阐述。值得注意的是，上述研究成果主要针对一级边坡支护机理进行相关分析，取得了有益的进展，而对多级边坡研究较少，且目前国内外大多模型试验的加载方式是侧向水平加载或者竖向加载，无法真实地模拟边坡实际变形特征并且功能单一。基于以上问题，设计了一种新型加载方式的模型箱，采用侧向非均匀加载方式最大程度地还原了边坡实际变形特征，即边坡侧向变形过程中上部位移大、下部位移小的特点。

基于此，本文通过室内模型试验，结合有限元数值模拟，对织物袋挡墙支护下二级边坡在侧向非均匀加载条件下的位移及土压力进行了研究，分析破坏模式并对其承载能力进行评价，以期获得规律性认识，为今后的理论研究和设计应用提供有价值的参考。

1 试验概况

1.1 试验材料

以坡高普遍在2 m以内的陕南梯田为原型，将原型与模型边坡的几何相似比设定Cl=4，基于相似定理，推导出原型与模型土样密度相似比Cρ=1，重力加速度相似比尺Cg=1，最终建立了室内缩尺模型边坡。模型采用二级黄土边坡，模型边坡尺寸为202 cm×64 cm×110 cm，黄土的物性指标见表1。

表1 黄土的物性指标

模型试验用的织物袋尺寸为11.0 cm×20.5 cm，填充大约袋体体积的80%，织物袋实物见图1a，填充完成后用塑料扎带封口并压实。为了较为真实地还原实际工程，层间织物袋采用连结扣联结见图1b，连接扣使用图钉和木板来代替[22]，尺寸为10.0 cm×4.0 cm×1.5 cm。

a)织物袋

1.2 试验设备

试验设备主要采用侧向非均匀加载边坡模型箱见图2，侧向非均匀加载系统中的侧压板的下端与模型箱底部铰接，上端左侧铰接于油缸活塞，工作机理为：液压设备推动活塞运动，活塞推动侧压板，使其以下端连杆支座为转轴转动。在加载过程中以二级边坡左侧底脚为轴，侧向非均匀加载侧压板顶部每级位移推进5 cm，共推进6级位移30 cm，每级加载结束记录一次位移及土压力。通过侧向非均匀加载较真实地模拟了现实情况下，上部滑坡对下方边坡、梯田、河堤、路堤等的推动作用，还原了下方边坡受到上部滑坡推动后的实际变形特征，即侧向变形过程中上部位移大、下部位移小的特点，如二级梯田，坡高较低，田面种植农作物，当受到侧向力时发生变形破坏。

a)非均匀加载装置

1.3 试验方案

本试验以坡比1.0∶0.5的边坡为研究对象，通过侧向非均匀加载系统，开展了3种支护条件下边坡的侧向加载模型试验。传感器埋设位置见图3，Pn、An分别表示土压力盒和位移传感器。试验过程中，侧向非均匀加载侧压板顶部共推进6级位移，每级位移推进5 cm。

a)单坎型

2 试验结果与分析

2.1 试验现象分析

图4为单坎型支护边坡的试验现象。由图可知：第一级侧推位移时，在靠近二级边坡坡面的位置处产生多条微裂隙，二级边坡坡脚处产生约3 cm的裂缝，距坡脚约18 cm处产生约5 cm的裂缝；第二级侧推位移时，二级边坡坡脚处的裂缝往上延伸至12 cm，距坡脚18 cm处裂缝延伸至15 cm，一级边坡开始出现多条微裂隙且距坡脚21 cm处出现7 cm裂缝；第三级侧推位移时，二级边坡距坡脚18 cm处裂缝延伸至27 cm，一级边坡距坡脚21 cm处裂缝延伸至约15 cm；第五级侧推位移时，产生贯通裂缝，由图钉示踪点可看出贯通裂缝上下相邻的图钉间发生错位，二级边坡距坡脚18 cm处和一级边坡距坡脚21 cm处出现明显的剪出口；第六级侧推位移时，坡体破坏程度加剧，且二级边坡比一级边坡破坏程度大，且二级边坡坡顶的变形最大，有约2.7 cm的拱起。

a)侧向变形

图5为L坎型支护边坡的试验现象。由图可知：第一级侧推位移时，在靠近二级边坡坡面的位置处产生多条微裂隙，二级边坡坡脚即第一排竖向埋置的织物袋处产生约3 cm的裂缝；第二级侧推位移时，二级边坡坡脚处的裂缝往上延伸至9 cm，一级边坡距坡脚17 cm和32 cm，即第二、三排竖向埋置的织物袋处产生约5 cm的裂缝；第三级侧推位移施加后，二级边坡坡脚处裂缝延伸至约20 cm，一级边坡距坡脚17 cm处裂缝延伸至约10 cm；第五级侧推位移时，产生贯通裂缝；第六级侧推位移时，坡顶出现约3.3 cm的拱起，竖向埋置的织物袋处出现裂缝。不同于单坎型支护，竖向埋置的织物袋增加了与土体的摩擦和挡墙自重，支护效果增强，使二级边坡中部无裂缝产生，仅从坡脚处延伸发展，一级边坡裂缝由第二排竖向埋置的织物袋处延伸发展。

a)侧向变形

图6为反坡L坎型支护边坡的试验现象。由图可知：第一级侧推位移时，靠近二级边坡坡面的位置产生多条微裂隙，二级边坡第二排竖向埋置的织物袋处产生约2 cm的裂缝；第二级侧推位移时，二级边坡第二排竖向埋置的织物袋处裂缝向第三排竖向埋置的织物袋处延伸，一级边坡距坡脚13 cm和25 cm，即第二、三排竖向埋置的织物袋处产生约4 cm的裂缝；第三级侧推位移时，二级边坡裂缝延伸至约22 cm，一级边坡距坡脚13 cm处裂缝延伸至约10 cm；第五级侧推位移时，产生贯通裂缝，二级边坡裂缝发展到3 cm宽，一级边坡裂缝达2 cm宽，且坡顶出现约4.3 cm的拱起。不同于单坎型和L坎型支护，由于织物袋袋体倾斜，最上层织物袋用土覆盖夯实，大大增强了抗滑动、抗转动和抗鼓肚能力，稳定性和支护效果增强，使二级边坡中部无裂缝产生，仅从坡脚处延伸发展。

上述分析说明：二级边坡为滑动型破坏，且二级边坡的破坏程度更严重，裂缝均产生于坡脚和距坡脚1/3～1/2高度处；L坎型和反坡L坎型支护下坡顶拱起高度较单坎型分别增大22.2%和59.3%。

a)侧向变形

2.2 坡体水平位移分析

图7为单坎型支护边坡的水平位移。由图可知：第一级侧推位移时，二级边坡坡顶处位移达到最大值为5.2 cm，一级边坡坡顶位移仅0.6 cm，侧向变形很小；前四级侧推位移过程中，水平位移的增幅较为均衡，二级边坡坡顶增量约3.6 cm，二级边坡坡脚位移增量约2.8 cm，一级边坡坡顶位移增量约2.1 cm；第五级侧推位移时，边坡发生破坏，位移增量显著变大，二级边坡坡顶位移19.8 cm，坡脚位移13.4 cm，一级边坡坡顶位移9.1 cm；第六级侧推位移时，二级边坡坡顶处侧向变形为22.2 cm。

图8为L坎型支护边坡的水平位移。由图可知：第一级侧推位移时，二级边坡坡顶处位移最大为4.6 cm，一级边坡坡顶处位移仅0.4 cm，侧向变形很小；前四级侧推位移过程中，水平位移的增幅较为均衡，二级边坡坡顶增量约3.1 cm，二级边坡坡脚位移增量约2.7 cm，一级边坡坡顶位移增量约1.8 cm；与单坎型支护不同，第五级侧推位移时边坡破坏，二级边坡坡顶位移为17.7 cm，坡脚位移11.9 cm，一级边坡坡顶位移7.8 cm；第六级侧推位移时，二级边坡坡顶处侧向变形为21.1 cm。

图9为反坡L坎型支护边坡的水平位移。由图可知：第一级侧推位移时，二级边坡坡顶位移最大为4.1 cm，一级边坡坡顶位移仅0.3 cm；前四级侧推位移过程中，水平位移的增幅较为均衡，二级边坡坡顶增量约3.2 cm，二级边坡坡脚位移增量约2.7 cm，一级坡边坡顶位移增量约1.6 cm；第五级侧推位移时，边坡发生破坏，位移增量无较大变化，二级边坡坡顶位移17.1 cm，坡脚位移11.1 cm，一级边坡坡顶位移6.9 cm；第六级侧推位移时，二级边坡坡顶处侧向变形为20.3 cm。

上述分析说明：二级边坡水平位移大于一级边坡，且边坡最大水平位移位于坡顶处；L坎型和反坡L坎型支护下坡顶水平位移较单坎型分别减小5.0%和8.6%，表明单坎型、L坎型和反坡L坎型支护下边坡抵抗侧向变形的能力递增。

a)距坡脚不同高度处坡体水平位移变化曲线

a)距坡脚不同高度处坡体水平位移变化曲线

a)距坡脚不同高度处坡体水平位移变化曲线

2.3 墙后土压力分析

图10为单坎型支护边坡的土压力。由图可知：第一级侧推位移时，不同测点处土压力大小不一，P3位于两级边坡的交接处，土体挤压最严重，土压力盒上覆土体重度最大，导致此处土压力最大，一级边坡中，P6处土压力最大；第二至五级侧推位移时，由于土压力盒上覆土体压密，导致土体重度增大，引起土压力增大，各个测点处的土压力均呈线性增大趋势，其中P3处土压力增幅最大；第五级侧推位移时，边坡出现贯通裂缝，P1、P2和P5处土压力盒位于贯通裂缝附近土压力最大，P3、P4和P6处土压力盒位于贯通裂缝前，无裂缝贯穿，土体持续压密，土体重度不断增大，土压力相应增大；第六级侧推位移时，土压力最大分别为19.23、7.45、9.47 kPa。

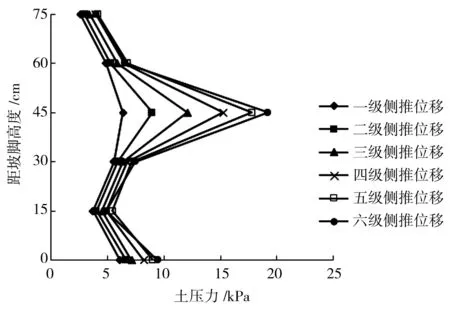
a)距坡脚不同高度处土压力变化曲线

图11为L坎型支护边坡的土压力。由图可知：第一级侧推位移时，P3处土压力最大，一级边坡中P6处土压力最大；第二至五级侧推位移时，与单坎型支护相似，各个测点处土压力均呈线性增大趋势，P3处土压力的增幅最大；第五级侧推位移时，边坡出现贯通裂缝，P1、P2和P4处土压力盒均位于贯通裂缝附近土压力最大，P3、P5和P6处土压力盒位于贯通裂缝前，由于土体持续压密，土体重度不断增大，土压力也相应增大；第六级侧推位移时，土压力最大分别为21.37、7.97、11.81 kPa。

a)距坡脚不同高度处土压力变化曲线

图12为反坡L坎型支护边坡的土压力。由图可知：第一级侧推位移时，P3处土压力最大，一级边坡中，P6处土压力最大；第二至四级侧推位移时，各个测点处的土压力均呈线性增大趋势，其中P3处土压力增幅最大，P1处产生2 cm的裂缝使土压力盒脱空，土压力骤减，P1处土压力最大值在第四级侧推位移后产生；第五级侧推位移时，边坡出现贯通裂缝，P2和P4处土压力盒均位于贯通裂缝附近土压力最大值，P3、P5和P6处土压力盒位于贯通裂缝前，土压力持续增大；第六级侧推位移时，土压力最大分别为22.93、10.23、12.86 kPa。

a)距坡脚不同高度处土压力变化曲线

上述分析说明：土压力随墙高的增加而增大，且一级边坡坡顶处土体对二级边坡与一级边坡连接处土体的侧向变形产生约束作用，致使该处土体挤压严重，土压力激增而产生最大土压力；L坎型和反坡L坎型支护下二级边坡P3处土压力较单坎型分别增大11.1%和19.2%，表明单坎型、L坎型和反坡L坎型抵抗侧向土压力能力依次增强。

3 二级边坡侧向承载特性数值计算

3.1 数值模型建立

采用ABAQUS软件建立相应的数值模型，二级边坡模型采用弹性本构及Mohr-Coulomb屈服准则进行模拟，相关参数为：密度ρ=1.45 g/cm3，弹性模量E=30 MPa，泊松比μ=0.3，内摩擦角φ=26°，黏聚力c=16 kPa；织物袋模型采用弹性本构，相关参数为：弹性模量E=200 MPa，泊松比μ=0.2。

在装配模块中导入边坡和织物袋部件，设置部件为非独立，经平移和阵列组装为整体，从而构成一个织物袋挡墙支护的二级边坡模型。模型中织物袋与织物袋，织物袋与边坡之间均设置接触，采用考虑切向及法向的摩擦接触。织物袋之间设置极限剪切应力1 500 N来模拟联接扣，当切向力超过极限剪切力，联接扣脱开，之后织物袋袋间的摩擦接触，摩擦系数取0.4，法向设置为硬接触；织物袋与边坡之间摩擦系数取0.3，法向为硬接触，相互作用均设置为表面与表面接触。

在初始分析步中对边坡底部xoz面约束3个方向的自由度，边坡两侧xoy面限制U3，即z方向的变形，边坡基层右侧限制U1，即x方向的变形。在加载分析步中施加重力，且根据二级边坡的工程背景，如二级梯田，坡高较低，田面种植农作物，当受到侧向力时发生变形破坏，加之为模拟模型箱侧压板的工作机理，对边坡右侧yoz面设置一个非均布位移来模拟坡顶侧推位移，见图13。

a)单坎型支护边坡的边界条件

二级边坡及织物袋均采用C3D8单元，为了便于网格划分，在部件模块中对边坡设置了基准面，见表2，近似全局布种尺寸0.05，完成网格划分后，即可运行作业命令提交模型进行计算。

表2 各部件单元类型及网格划分

3.2 模拟结果分析

图14为不同支护下二级边坡的侧向变形，由图可知：模型试验得到的侧向变形与数值计算得到的基本相同，二级坡坡顶侧向变形最大，且有拱起现象，同时织物袋变位模式为每级边坡上部3/5墙高的织物袋是平动的，墙体下部2/5的部分为绕墙底部的转动。

a)单坎型

图15为不同支护下二级边坡水平位移云图。由图可知：单坎型支护的二级边坡坡顶、坡脚水平位移分别为24、14 cm，一级边坡坡顶、坡脚水平位移分别为11、3 cm；L坎型支护的二级边坡坡顶、坡脚水平位移分别为23、13 cm，一级边坡坡顶、坡脚水平位移分别为10、3 cm；反坡L坎型支护的二级边坡坡顶、坡脚水平位移分别为23、11 cm，一级边坡坡顶、坡脚水平位移分别为9、2 cm。对比可以发现，单坎型支护二级边坡水平位移最大，L坎型支护边坡其次，反坡L坎型支护边坡水平位移最小，模型试验测得的水平位移与数值计算得到的规律基本相同。

a)单坎型

图16为不同支护下二级边坡模型试验数据与数值计算结果对比。由图可知：模型试验得到的各个测点的坡体水平位移测试结果与数值计算得到的坡体水平位移变化规律基本相同。

a)单坎型

图17为不同支护下二级边坡塑性应变云图。由图可知：各工况下最大塑性破坏均发生二级边坡坡脚处，并以滑动塑性区的形式向坡顶发展，在滑弧的发展过程中，塑性应变集中的情况逐渐缓解，塑性区渐变更均匀，且二级边坡比一级边坡塑性破坏严重，L坎型和反坡L坎型在竖向埋置的织物袋处土体塑性应变较大。可以发现：单坎型织物袋挡墙支护二级边坡塑性破坏最严重，L坎型支护边坡其次，反坡L坎型支护边坡塑性破坏最小，模型试验得到的滑裂面位置与数值计算得到的塑性区分布基本吻合。

a)单坎型

4 结论

本文通过侧向非均匀加载模型箱进行室内模型试验，选取黄土二级边坡为研究对象，实测单坎型、L坎型和反坡L坎型支护条件下的二级边坡坡顶竖向位移、坡体水平位移和挡墙后土压力的变化，分析二级边坡侧向破坏模式，并进行相应的承载能力评价，同时运用ABAQUS有限元软件，分析验证了单坎型、L坎型和反坡L坎型织物袋挡墙支护下的二级边坡侧向变形及塑性区分布，主要得到以下结论。

a)在侧向非均匀加载作用下，二级边坡先于一级边坡发生破坏且破坏程度较一级边坡严重，尽管裂缝开始发展的部位不同，但均从坡脚和距坡脚1/3～1/2高度处产生并延伸发展。

b)在侧向非均匀加载作用下，反坡L坎型织物袋挡墙支护的二级边坡破坏前能够承受更大的侧推位移和土压力，且侧向变形和破坏程度最小，故承载能力最高，其次为L坎型支护边坡，单坎型支护边坡承载能力最低。

c)在侧向非均匀加载作用下，二级边坡均为滑动型破坏，随着支护强度的增大，滑裂面或贯通裂缝的深度依次增大。

d)通过ABAQUS有限元软件对3种织物袋挡墙支护方式的二级边坡进行数值模拟，通过数值计算结果分析可以得出：模型试验得到的各个测点的侧向变形测试结果与数值计算得到的侧向变形规律基本相同，且最大塑性破坏均发生在二级边坡坡脚处，二级边坡比一级边坡塑性破坏严重。