均质与非均质土中水动力弥散规律研究

王 达，庄鲁文，林凯荣，冯上超

(中山大学土木工程学院，广东 珠海 519082)

当前随着土壤盐渍化和地下水污染问题的逐渐加剧，研究土壤中溶质的运移和分布特征，定量分析均质土及非均质层状土壤中的水盐运移规律，对于掌握和控制污染物的迁移扩散范围，改良盐渍土意义重大[1-3]。与此同时，探究不同因素[4-6]对水动力弥散系数及溶质运移过程的影响，对于准确预报溶质污染物在土壤地下水中的迁移扩散规律具有重要理论与应用价值。其中水动力弥散系数是表征土壤地下水中污染物迁移和分布的重要参数，代表着溶质在多孔介质中弥散作用的强弱[7-10]。

在此背景之下，国内外大量学者相继开展了相关研究。其中通过对比研究均质土与非均质层状土中溶质迁移规律，是当前最常见且有效的方法[11]。已有研究表明，当细土覆盖粗土产生上细下粗型层状结构时，水分在细砂和粗砂界面会被滞留，当湿润锋穿过粗细土界面时会产生指流现象，入渗率趋近于常数[12-13]。而对于上粗下细型层状土，导水率较低的下层细砂土会降低上层砂土水分再分布的速率，从而会提高层状土壤的持水能力[14]，所以非均质层状土中的溶质扩散迁移时，由于土壤上下层质地的不同，层状结构对溶质扩散的分散系数以及流速影响很大，不同土层的排序使得溶质在同一情境下产生的穿透曲线区别也很大[15]。此外，同一种溶质在均质土与非均质层状土中的弥散度具有明显差异，并且这种差异与夹层土壤的弥散度密切相关，层状土的水动力弥散系数不是均质土水动力弥散系数的平均值[16]。不同尺度下模拟试验的结果也不尽相同，因为在层状土中进行不同尺度下的溶质迁移扩散试验时，由于土壤介质的非均匀性，溶质迁移扩散时会产生尺度效应[17]，但当前对此还尚无确切的定论。因此，为进一步研究均质土与非均质层状土中水动力弥散的规律[18]，进行均质土壤和非均质层状土壤中溶质运移的试验与数值研究十分有必要。

1 材料与方法

1.1 试验土样基本物理性质

选取粗细不一的2种标准沙，就均质土与不同构型的层状土溶质运移进行试验研究。其中2种砂土的基本物理特性见表1。

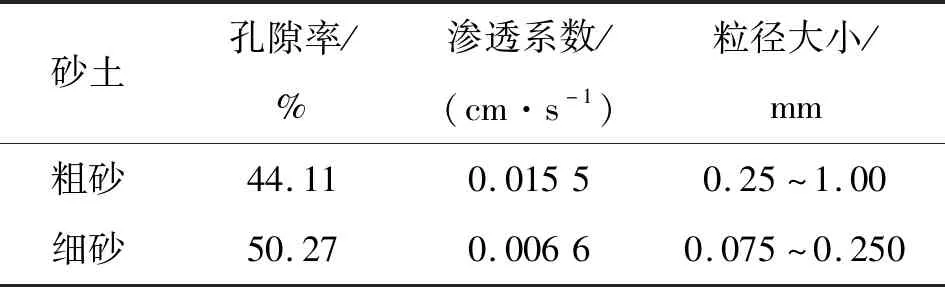
表1 试验土样基本物理性质

在进行溶质迁移试验之前，为进一步验证所选土样的代表性，检测砂土持水与失水性能，经过测量以及经典的VG[19]模型拟合得出2种砂土的毛管压力曲线，见图1。

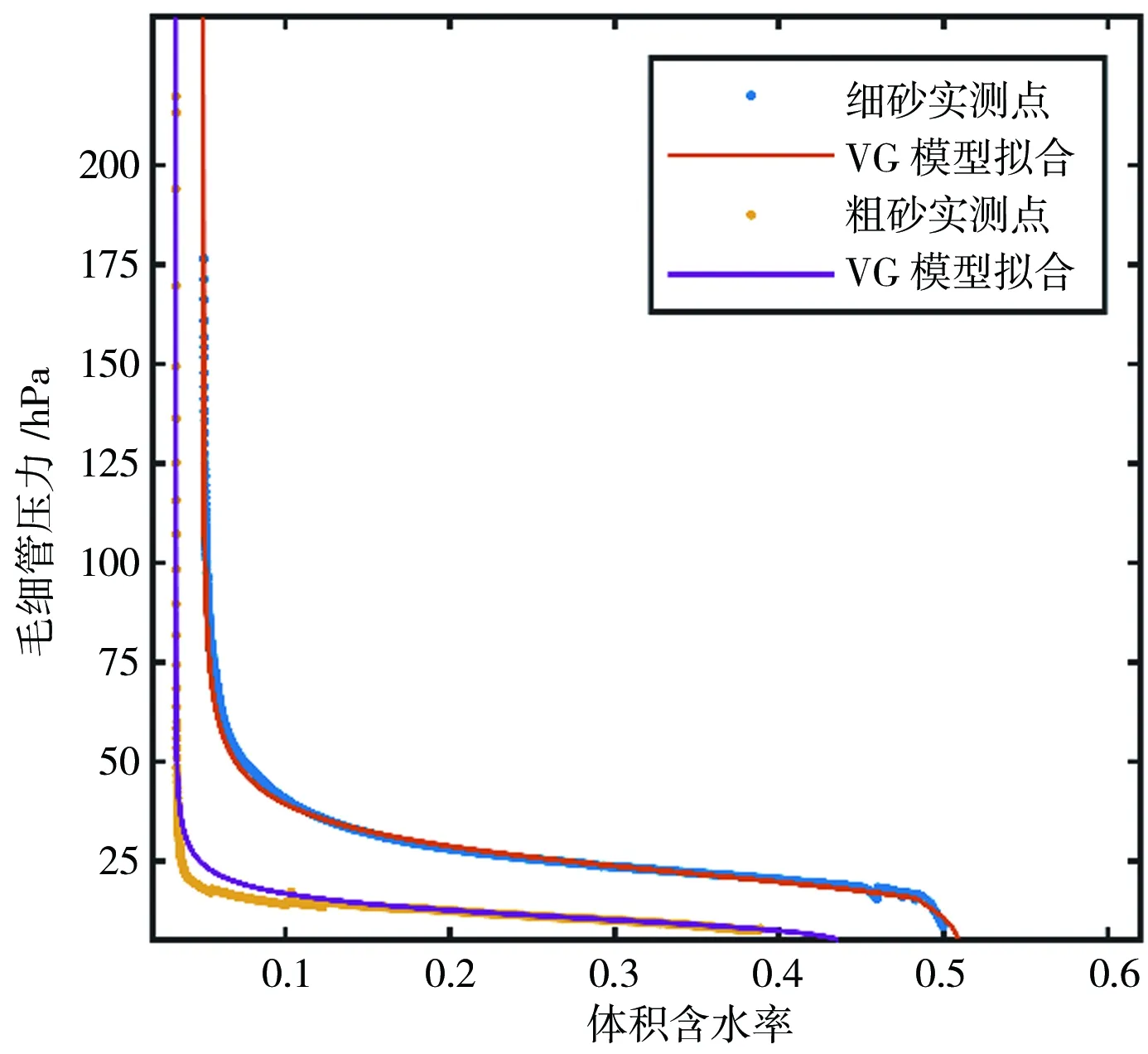
图1 2种砂土的毛管压力曲线

1.2 试验装置

为对比分析均质土与非均质层状土中的溶质迁移扩散规律，设计了长40 cm和短21 cm、材料完全一致、高度不同的2种玻璃柱进行土柱试验。其中21 cm的柱子由下至上在7、14 cm处分别装有一个探针传感器，主要用于均质土中溶质迁移扩散的试验研究，而40 cm长的柱子由下至上在8、16、24、32 cm处各装有一个探针传感器，主要用于非均质层状土中溶质迁移扩散的试验研究。其中示踪剂为NaCl溶液。试验整体装置见图2。

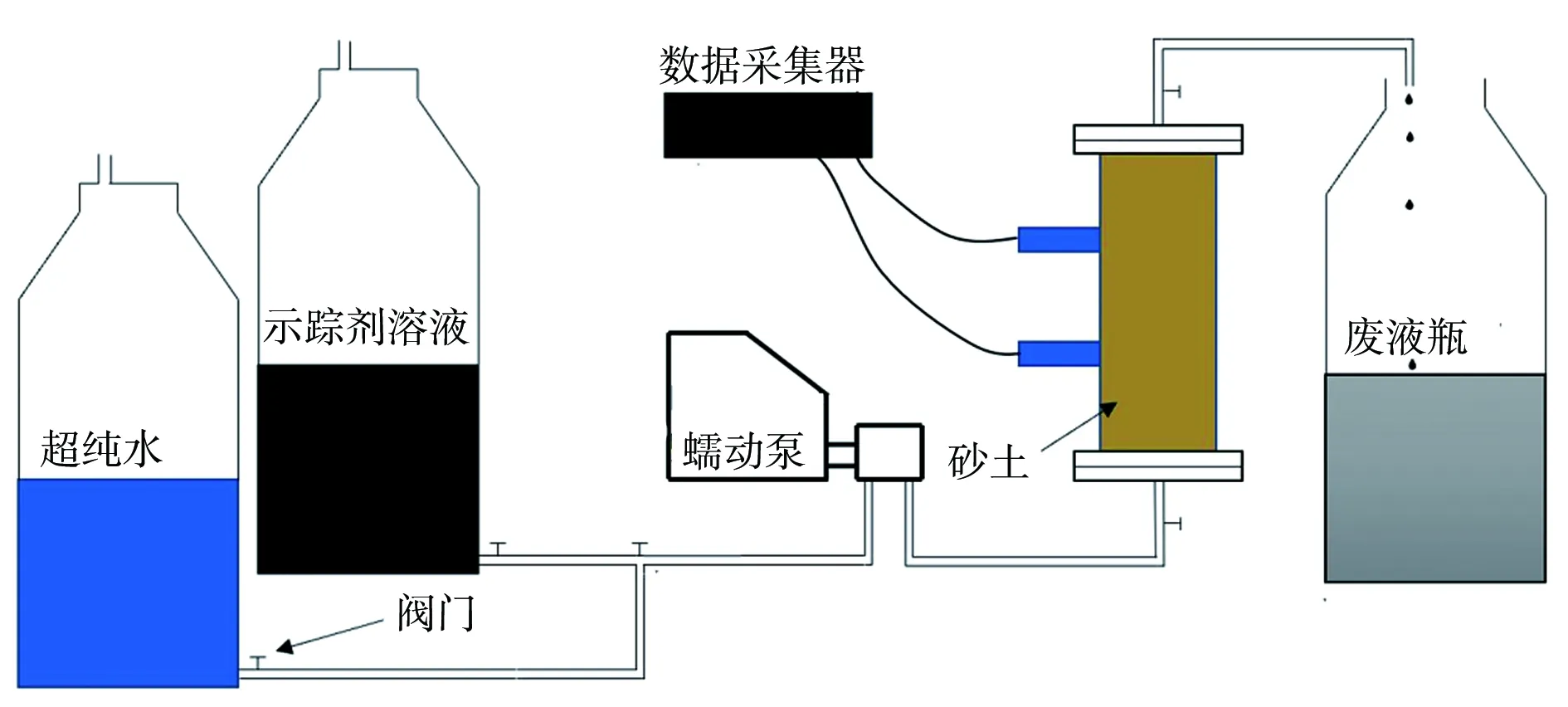
图2 试验装置示意

1.3 试验方法

试验分成三大组。其中第一、第二大组使用21 cm玻璃柱分别对粗沙和细沙进行不同溶液浓度和不同流速下的溶质迁移扩散试验，用于探讨溶质浓度、流体流速及多孔介质粒径大小等因素对均质土壤中水动力弥散的影响。而第三组为粗沙和细沙混合形成不同层状结构后的试验，使用40 cm长的土柱进行不同尺度的试验。2种砂土按体积1∶1进行混合，混合工况见图3。在同一示踪剂浓度下进行不同流速下的溶质运移试验，用于探讨层状非均匀性对水动力弥散的影响。在试验前使用去离子水对2种砂土分别进行清洗，去除混合杂质的干扰。在试验中由下向上先通入超纯水，待土壤饱和且水流稳定后再通入NaCl溶液，其中溶液通入的开始时间与达西流速均可通过阀门与蠕动泵进行控制。最后通过插入的探针传感器实时读取土柱中溶液的相对浓度。

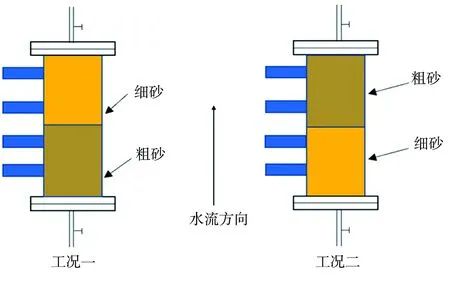
图3 非均质层状土试验工况

2 传输模型

由于在整个入口横截面上溶质是均匀注入的，并且横向边界上无流动，装置中整体宏观流动和溶质传输仍然可以被认为是一维的，可以使用一维连续尺度模型来模拟溶质穿透曲线，因此本文选取经典的对流扩散方程(ADE方程)[20]来描述非吸附性溶质运移过程，其中对流扩散方程如下：

(1)

式中C——平均溶质浓度；z——纵向迁移距离；t——时间；D——水动力弥散系数；v——平均孔隙水速度。

假设在初始无溶质分布的入口(z=0)处施加一个持续时间较短的溶质脉冲，即提供相应的初始条件、边界条件和相应的数据点时，便可以进行求解。其中使用的边界条件和初始条件如下：

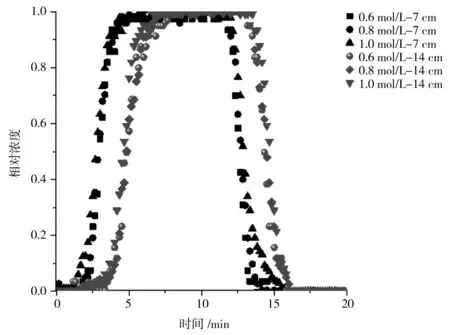
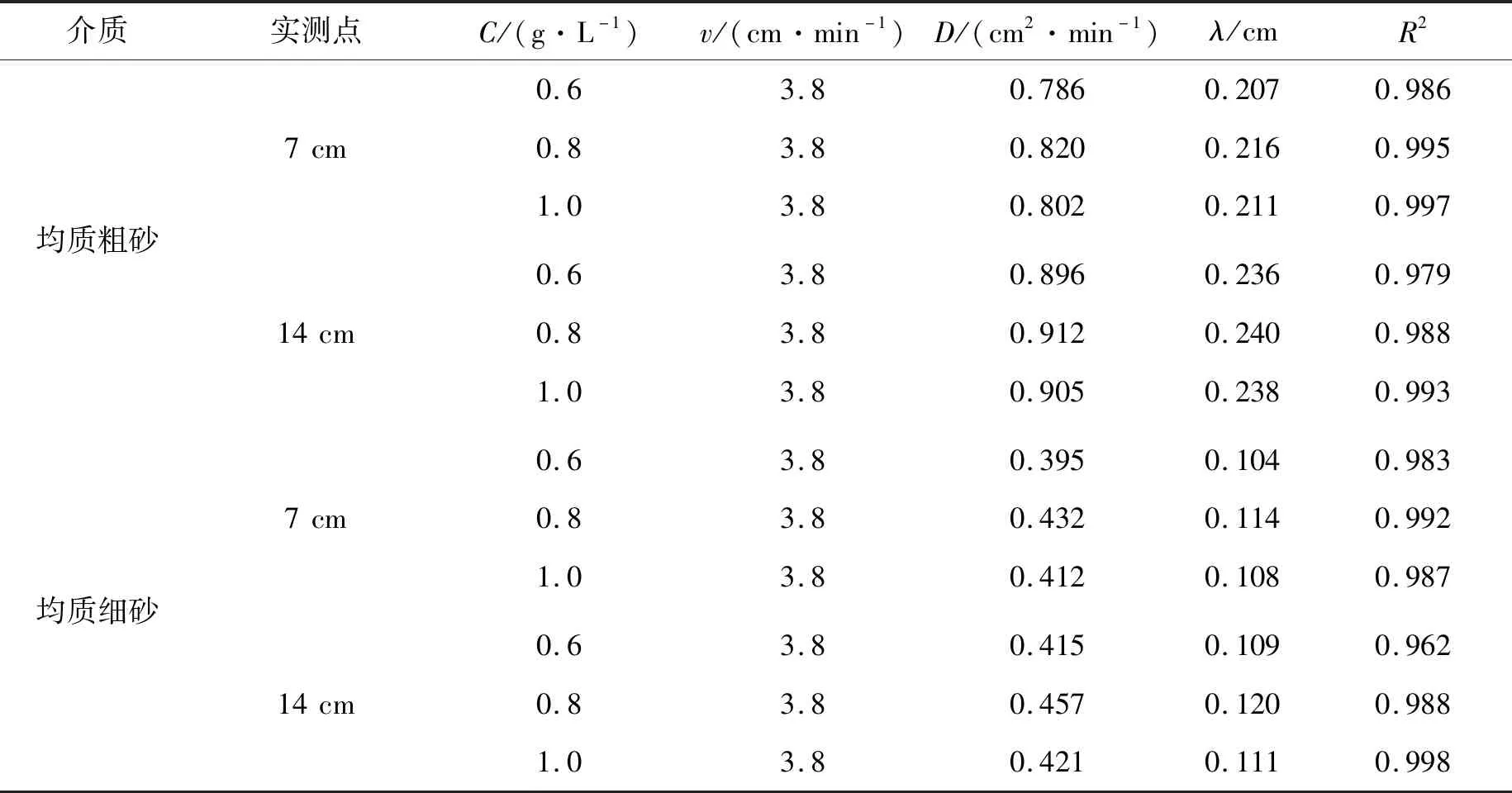
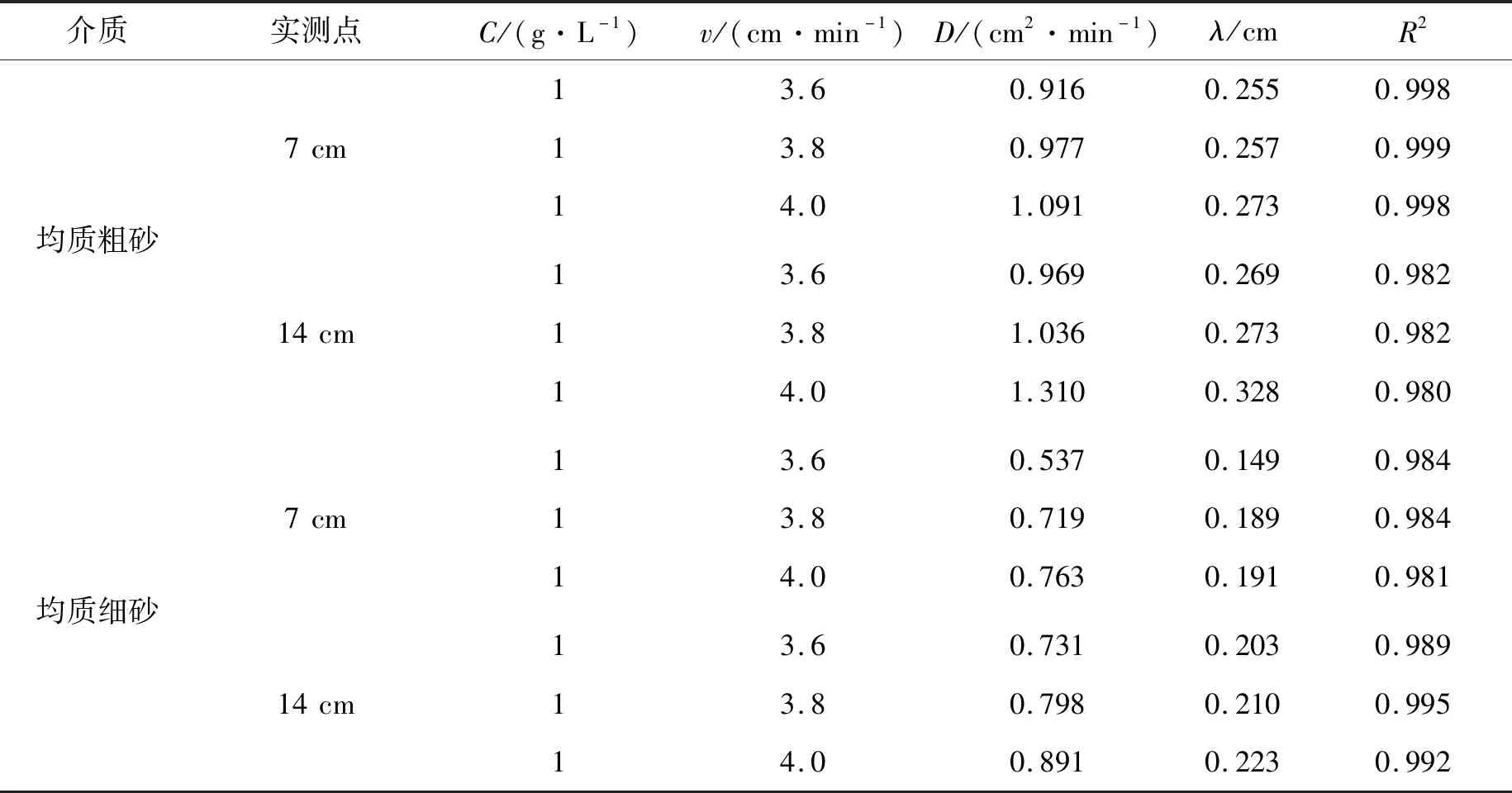
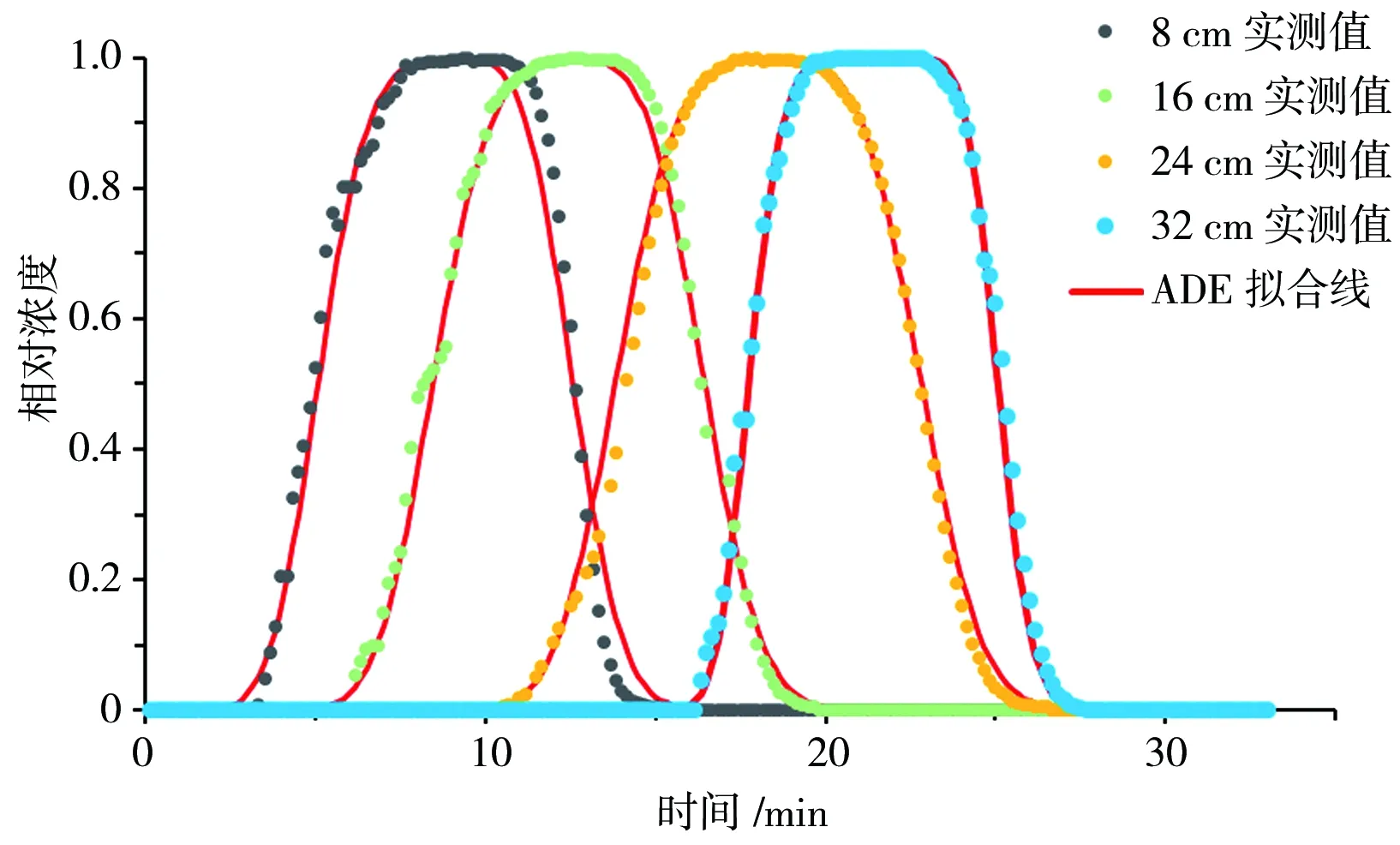
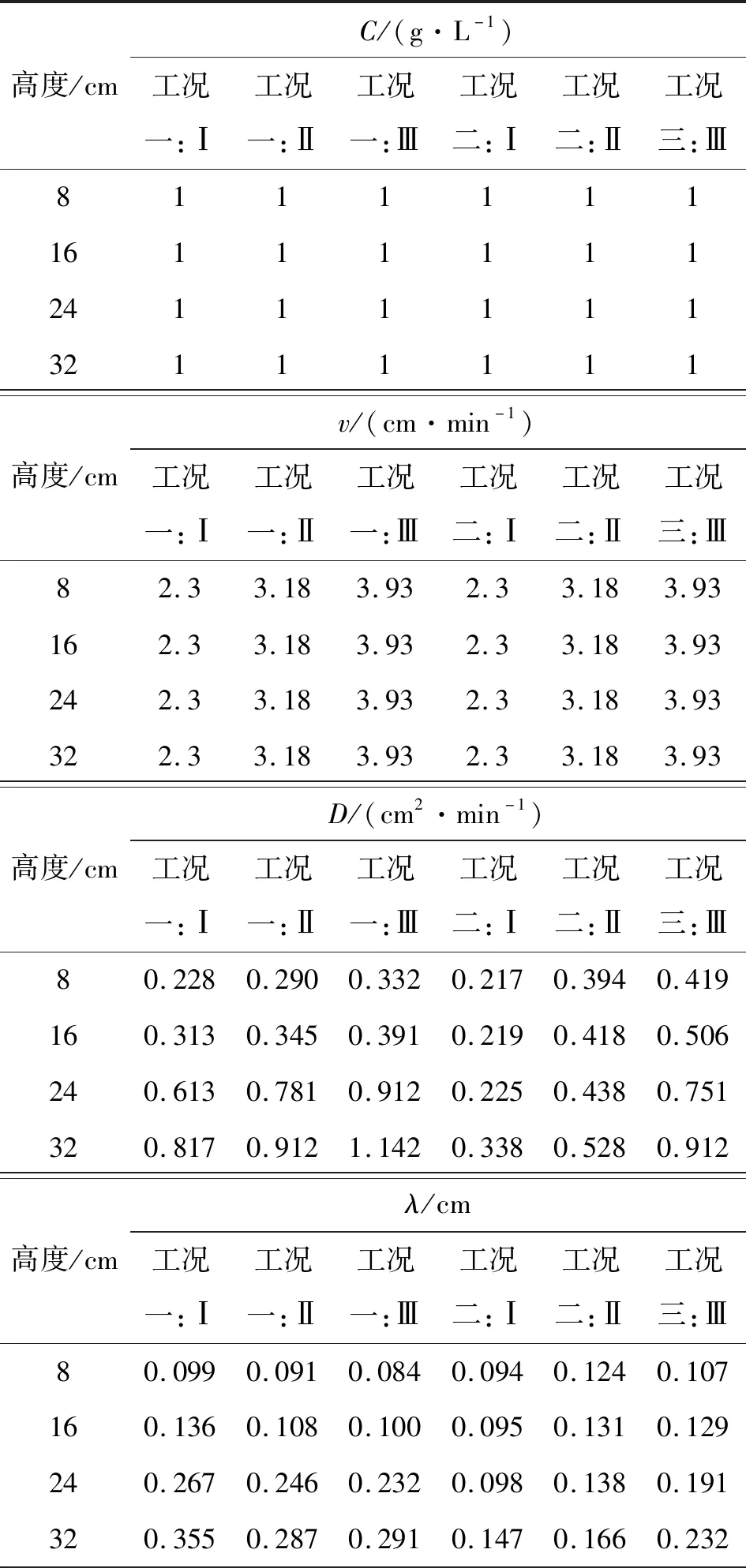
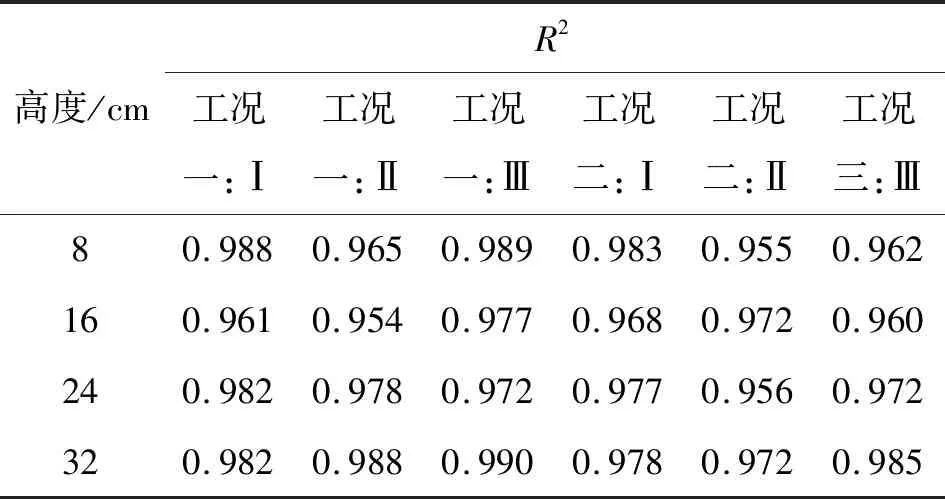
C(z,0)=0，0

(2)

(3)

(4)

式中C(z,t)——溶液浓度；CR——相对浓度；L——土柱的长度。

在水动力弥散系数计算过程中，通过土柱中每个位置所观测到的数据，基于对流扩散方程，使用CXTFIT计算机程序[21-22]来估计式(1)中的参数v和D，及对应的迁移试验中观察到的穿透曲线(BTCs)。其中CXTFIT程序是根据给定初始值代入选定运移模型后，使用非线性最小二乘法无限逼近实测值从而得出观测数据与对流扩散方程之间的最佳拟合值。

在一维溶质运移过程中，饱和均质与非均质层状土中的多孔介质，流体水动力弥散系数是分子扩散和机械弥散函数的总和，后者是局部速度变化的结果，计算关系见式(5)[20,23]：

D=De+λvn

(5)

式中De——有效扩散系数；λ——弥散度，定义为λ=D/v，n主要是经验参数，取为1。

式(5)所示，水动力弥散包括离子或分子弥散(De)和溶质平流过程引起的机械弥散(λvn)。

3 结果与讨论

3.1 均质土溶质穿透曲线特性分析

土壤溶质运移穿透曲线(Breakthrough Curve,BTCs)是反映流液溶质相对浓度随时间或孔隙体积变化的曲线，可描述溶质在土壤中迁移扩散的不同特征。其中2种均质砂土在不同浓度和不同流速条件下的柱试验模拟结果分别见图4、5。其横纵坐标为土柱中溶质运移穿透时间，纵坐标为溶质相对浓度。当溶质相对浓度达到1并保持稳定时，表明穿透的溶质达到饱和，主要穿透过程已结束，后续可以停止通入溶液观察不同条件下土壤失水并排出溶质的尾迹过程。

a)均质粗砂

a)均质粗砂

由图4中土柱7、14 cm不同深度处的穿透曲线可知，溶质浓度从0.6 mol/L逐渐增大到0.8、1.0 mol/L的过程中，同一深度处的溶质穿透曲线几乎一致没有产生改变，反映了溶度对穿透曲线的影响甚微；而由图5可知，流速从3.6 mol/L逐步增大到4.0 mol/L的过程中，溶质穿透曲线相应向左发生了偏移；其中浓度和流速增大对穿透曲线产生不同的影响，是因为在实际土壤中，水流速度增加或较大时，则机械弥散的影响大于分子扩散的影响，此时水动力弥散只需考虑机械弥散的作用；相反若流速较小，则只需考虑分子扩散作用，此时依靠的是分子的不规则运动而非土壤水分运动。在均质土中，一般浓度及流速增大，土壤溶质会更快达到饱和；且在同一条件下随着浓度及流速增大，均质粗砂比均质细砂的穿透曲线更先达到饱和，是因为细砂渗透率低，因此需要更长时间才能获得完整的BTCs。在不同条件下不同深度处的穿透曲线大体相似，表明土柱中溶质均匀分布，符合一维连续尺度下的对流扩散模型。

3.2 均质土溶质运移参数分析

基于前述对流扩散方程，使用CXTFIT程序将ADE模型解析解拟合到实测的穿透曲线中，以确定孔隙水速度v和溶质分散系数D的值，并由此计算溶质弥散度λ。其中对于2种均质土不同浓度及流速下的柱试验穿透曲线拟合结果分别见表2、3。所有试验的观测数据与预测数据回归的R2值均超过0.95接近于1，表明拟合度高、可靠度强。

表2 均质土中不同浓度下溶质运移拟合参数

表3 均质土中不同流速下溶质运移拟合参数

由表2、3可知，溶质的浓度对水动力弥散系数的影响非线性正相关，而达西流速与弥散系数大体成正相关，这与式(5)关于水动力弥散系数定义一致，表明分子扩散并不受达西流速的影响，但达西流速对机械弥散的影响不容忽略。且不同高度处传感器探针测量值不同，表明水动力弥散系数随溶质迁移距离的不同而有所不同，一般迁移距离越远，纵向弥散系数越大[24-25]。

通过对比溶质在2种不同介质中的弥散系数大小可知，在同一流速下，水动力弥散系数与砂土的平均粒径存在正相关关系，平均粒径较大的粗砂的弥散系数受孔隙水流速度的影响较大，平均粒径小的细砂弥散系数受孔隙水速度的影响小，这与早期的一些研究一致[26-28]。此外，弥散度也随达西流速及迁移距离的增大而增大，而溶质浓度对弥散度的影响相对较小。

3.3 非均质层状土溶质穿透曲线特性分析

在完成上述2组均质土壤溶质迁移试验后，在40 cm土柱中进行了非均质土2组工况不同流速下的溶质运移试验。通过试验观测得知不同流速下的穿透曲线整体几乎一致。其中某一流速下同时对应的4个不同高度处(8、16、24、32 cm)的出流物的BTCs穿透曲线见图6，2组工况中溶质穿透曲线不完全相同，而使用对流扩散方程模拟的宏观尺度(连续尺度)下的穿透曲线与试验数据之间的一致性良好，BTCs的对称形状也符合一般溶质迁移的研究[29]。在2组各自的条件下，溶质先经过粗砂的弥散再进行细砂弥散，或者经细沙到粗砂，从而使8、16 cm处为均质弥散，而24、32 cm处记录的是非均质土中的水动力弥散。与均质土壤相比，非均质条件下溶质穿透曲线所需时间相对长一些，可能是非均质土中存在较大孔隙及优先流等因素，不同土层中溶质迁移距离越远，穿透曲线也更长。同时非均质层状土中不同土层排序下的穿透曲线不一样，下层砂土粒径越大，溶质穿透时间越早。

a)工况一

3.4 非均质层状土溶质运移参数分析

不同工况及流速下的非均质层状土溶质运移拟合参数见表4，在层状土中，水动力弥散大小仍然随着流速的增大而增大，同时也随着溶质迁移距离的增大而增大[4,24-25]。与前两组试验相比，不同尺度下的第三组试验中溶质迁移扩散时间更长，层状结构的非均匀性会影响溶质的纵向分散性，使水动力弥散系数减小，但在相同尺度下，均质土柱的弥散系数小于非均质土柱的弥散系数值。而第三组试验中，土层的排序也会影响溶质的穿透曲线[15]，同一种流速下迁移距离相同时，下层沙土粒径越大，则其水动力弥散系数越大，相对应条件下的弥散度也更大。

表4 非均质土不同流速下溶质运移拟合参数

续表4 非均质土不同流速下溶质运移拟合参数

与均质土壤介质相比，溶质在非均质层状土中迁移扩散时，水动力弥散系数受到分散性(λ)、孔隙水速度(v)、迁移距离(L)和平均粒径(d)等常见因素的共同作用，同时由于层状土的不均匀性、土层的顺序和土层厚度使得土层水势在界面发生突变，从而使得非均质层状土中的水动力弥散情况更为复杂。

4 结论

通过对不同条件下的均质非均质土进行柱试验与数值拟合，系统分析溶质迁移扩散的穿透曲线及水动力弥散现象，探究不同因素的下的溶质迁移扩散的一般性规律如下：①溶质的浓度对水动力弥散系数及穿透曲线影响甚微，而不同介质下的水动力弥散系数与水溶液流速均呈正相关关系；②同一流速下，水动力弥散系数与砂土的平均粒径存在正相关关系；平均粒径大的土壤受流速影响也相对较大；③不同位置处迁移扩散的水动力弥散系数不一致，由于溶质在土壤中的迁移扩散存在尺度效应，随着行进距离的增加，溶质分散性随着迁移距离的增加而增加；④非均质层状结构对层状土壤中的溶质水动力弥散也有着显著的影响，层状土壤的非均匀性会消减溶质的水动力弥散作用。