高速铁路全并联AT牵引网异相短路阻抗特性及影响规律研究
2022-12-02韩正庆刘淑萍高仕斌
沈 睿,韩正庆,刘淑萍,高仕斌
(西南交通大学 电气工程学院,四川 成都 611756)
我国的电气化铁路采用单相工频交流制供电,为减弱单相负荷对三相电网造成的不平衡,牵引变电所采用循环换相、分段供电[1],电分相被设置在两相邻供电臂间将不同相位的电隔离。由于列车带电闯分相、越区隔离开关误合、分相绝缘距离设置不合理等原因,异相短路故障时有发生,并可能进一步发展为接触网烧损等事故[2-3],造成巨大的损失。特别是在我国高速铁路规模大、里程长、密度高的背景下,电分相数量多、动车组速度快,导致异相短路故障增大。随着高速铁路的进一步建设和发展,异相短路故障带来的危害不容忽视,对异相短路故障展开深入研究,把握其故障特征,保障高速铁路行车安全,势在必行。
牵引供电领域的学者们对异相短路展开了系列研究,文献[4]采用变压器等值电路对异相短路进行定量分析,文献[5-7]在此基础上加入了微分方程构建的电弧模型进一步研究故障特征,并讨论了传统保护元件的适应性。文献[8]考虑了不同的联结组变压器及不同牵引负荷工况的故障特征。文献[9]讨论了异相短路中电弧的产生和发展规律,但未涉及异相短路的故障特征。
上述研究虽然对异相短路的产生、发展、特征和保护进行了探讨,并通过阻抗推导得到了故障时两供电臂的测量阻抗分别位于第二、第四象限的结论[4-8],但仍存在以下问题:
(1)相关结论的研究对象是普速铁路背景下的YNd11接线牵引变电所,且忽略了线路的影响,相关结论在变压器联结组不同、线路结构更复杂的高速铁路中并不完全适用。
(2)根据现场反馈的故障案例,异相短路时的测量阻抗也出现了落在第一、第三象限的情况[3],与过往的经验相矛盾。异相短路时阻抗角分布不一,在一定程度上影响了现场人员对故障类型的判断和事后对故障的分析。
(3)我国幅员辽阔,各线路的变压器类型、容量、线路长度等参数迥异,现场反馈的故障特征也存在差异,现有的分析方法仅针对单一变压器类型,不足以涵盖所有故障情景。
综上所述,既有研究对异相短路的阻抗特性及其影响因素的研究还不够彻底和全面。
距离保护是牵引供电系统的主保护[10],阻抗特性是故障分析的理论基础。为对异相短路故障展开深入、全面的分析,本文将追本溯源,考虑多种影响因素,以高速铁路全并联AT牵引网和牵引变压器的等值电路为基础,计及牵引变压器漏抗、线路阻抗、AT漏抗和牵引负荷,构建异相短路故障模型,化简推导异相短路故障分析电路和测量阻抗表达式,实现多参数、多线路、多工况的异相短路故障分析。在此基础上,研究过渡电阻、变压器联结组、变压器容量、牵引负荷和供电线长度等对阻抗的影响规律,揭示异相短路故障的阻抗特性。
1 异相短路故障回路
牵引变压器从三相电网取电变换为两相,分别向两条供电臂馈电,其中电压相位超前的称为“超前相”,相位滞后的称为“滞后相”。供电臂中有上行和下行两条线路,分别在变电所、AT所和分区所并联,图1为异相短路故障回路示意。

图1 异相短路故障回路示意
正常情况下,动车组在接近电分相时,接收到列车控制系统和地面装置的信号,断开车上的主断路器,切断从牵引网的取流,依靠惯性滑过电分相后,重新闭合主断路器恢复取流,因此正常情况下整个过程不会产生电弧。然而,由于地面装置失灵等原因,一旦动车组带电闯分相,受电弓与接触线间将形成电弧。电弧在多物理场的共同作用下拉伸、运动,若电弧往复运动、长时间燃烧,将发展为异相短路故障[9]。电弧燃烧过程中剧烈发热,引起接触线、承力索和吊弦的灼伤甚至烧损、烧断,最终酿成断线、塌网等事故。
当异相短路故障发生时,存在如图1所示的3条故障回路。最短的故障回路由电分相两端故障侧的馈线断路器和牵引变压器二次侧构成,该回路故障电流最大。此外还存在非故障侧经AT所和分区所迂回供电形成的两条故障回路。现有的牵引供电系统距离保护为准确识别接地短路故障,所采集的是变电所母线对地电压和馈线断路器电流。然而,异相短路中不存在对地故障回路,与常见对地短路的故障特征也存在较大差异。因此,本文在考虑异相短路独特性的基础上,从故障回路的化简合并出发,展开异相短路故障分析。
2 异相短路阻抗计算
为准确计算异相短路时的测量阻抗,应计及故障侧和非故障侧共三条故障回路。采用变压器等值电路和牵引网等值电路,并对电路进行合并化简,得到异相短路故障分析电路和测量阻抗表达式。
2.1 等值电路
2.1.1 AT牵引网等值电路
AT牵引网包括接触线(T)、钢轨(R)和正馈线(F),每隔一段距离设置一台自耦变压器(AT)。AT的两端分别连接T线和F线,中点经等效漏抗Zg连接在R线上,AT牵引供电系统见图2。
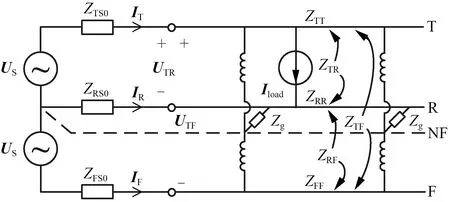
图2 AT牵引供电系统
图2中,UTR、UTF分别为变压器端口电压,IT、IR、IF分别为线路电流,ZTT、ZRR、ZFF分别为T线、R线、F线单位自阻抗,ZTR、ZTF、ZRF分别为三者的单位互阻抗,NF为牵引变压器和AT的理想中点连成的参考线。牵引变压器的Y型等值电路[11]参数ZTS0、ZRS0、ZFS0分别为
(1)
式中:ZS为电力系统归算到二次侧的阻抗;Z1、Z2、Z3分别为变压器原边绕组、T绕组、F绕组归算到二次侧的阻抗,其表达式为
(2)
其中,n为1、2或3,代表不同绕组;UTn%为对应绕组的短路电压百分比;UN为二次侧额定电压,取27.5 kV;ST为变压器容量。
AT等效漏抗Zg为
(3)
式中:UAT%为AT短路电压百分比;SAT为AT容量。
当Zg不为零时,列车的负荷电流Iload将流经各个AT,电流的分布复杂,但负荷电流与线路电流之间满足
IT-IF=Iload
(4)
依据式(4)的电流关系,根据戴维南定理,将图2中NF线作为等值的F′线,将AT解耦并消去T、R、F线间互阻抗,得到如图3所示的等值电路[12]。

图3 AT供电系统等值电路

(5)
2.1.2 牵引变压器等值电路
文献[15]中给出了ZTS和ZFS相等时的牵引变压器等值电路,为了不失一般性,考虑ZTS和ZFS不相等的情况。对图2中单相三绕组变压器列写电压回路方程为
(6)
代入式(5)中线路电流的等值关系,解得牵引变压器等值归算后的漏抗为
(7)
通过等值归算,将AT牵引网从包含有AT的复杂网络简化为简单的阻抗串并联网络,对全并联AT牵引网可以采用完全相同的方法进行等值归算,作为测量阻抗计算的基础。
2.1.3 等值电路下的测量阻抗表达式
已经证明[12],AT牵引网的T线和F线电流矢量差与各种故障电流存在以下关系
IT-IF=ITR=IFR=2ITF
(8)
式中:ITR、IFR、ITF分别表示T-R、F-R和T-F故障下的故障电流。
因此,AT牵引网的馈线保护测量阻抗被定义为各保护安装处的T线对地电压和T线、F线电流矢量差的比值[10],即
(9)
式中:i=1,2,…,表示不同的保护。
在AT牵引网等值电路中,由式(5)可知,原电路中T线对地电压等值为T′线对地电压,原电路中T线和F线电流的矢量差等值为T′线电流,式(9)变为
(10)
AT等值电路中的测量阻抗为保护安装处的等值T′线对地电压和等值T′线电流的比值。
2.2 异相短路故障分析电路和测量阻抗表达式
通常来说,高速铁路线路的上行和下行所采用的导线型号、线路布置是对称的且供电线长度相同,其线路参数相同、α相和β相供电臂长度相同。设变电所到AT所的距离为D1,AT所到分区所的距离为D2,过渡电阻为Zf。将图1所示的异相短路故障电路归算为AT牵引网等值电路见图4。

图4 全并联AT牵引网异相短路等值电路
图4中,UTRα和UTRβ分别为α相和β相供电臂馈线保护的测量电压,Iα1和Iα2分别为α相非故障侧和故障侧馈线保护的测量电流,Iβ1和Iβ2分别为β相非故障侧和故障馈线保护的测量电流,ZL为归算后的供电线阻抗。
将等值R′线、F′线和漏抗Zg合并为ZG,计算式为
(11)
进一步化简电路,异相短路故障分析电路见图5。

图5 异相短路故障分析电路
图5中,ZSα和ZSβ为将α相和β相的变压器等值漏抗与ZG合并而成的供电臂等效内阻。
(12)
列写回路电压方程,解得异相短路测量阻抗表达式,其中Zα1、Zα2、Zβ1和Zβ2分别为α相和β相的非故障侧和故障侧测量阻抗。
(13)
(14)
式中:Δθ为变压器两次侧绕组额定电压的相位差,由变压器联结组决定。

(15)
Z0与变压器漏抗、线路阻抗、过渡电阻等有关。
从图5中可以看出,非故障侧线路和故障侧线路的测量电流呈并联分流的关系,通常供电线的长度远小于线路的长度,故障电流仅有少部分流经非故障侧,故障侧的故障特征更加明显。因而本文主要探讨故障侧馈线保护测量阻抗的特性。
异相短路故障发生时,牵引变电所母线电压通常仅有小幅降落,牵引负荷可能仍能正常运行[12]。若要考虑牵引负荷对测量阻抗的影响,在图5所示故障分析电路的基础上增大负荷阻抗Zloadα或Zloadβ,列写回路电压方程后,能解得与式(13)类似的测量阻抗表达式。
除变电所处的电分相外,分区所也设置有电分相。现行设计要求两相邻变电所间供电分区同相[1],即分区所电分相两侧的电压相位相同,因此牵引网异相短路通常出现在变电所电分相。对于特殊情况下分区所不同相的系统,分区所处异相短路的故障分析过程与变电所处异相短路故障分析过程类似。
3 异相短路测量阻抗影响规律分析
对于确定的线路,其线路参数和变压器参数是固定的,而每次故障时的过渡电阻存在差异,且对于电弧故障,其过渡电阻随时间呈周期性、非线性变化[16]。因此,本文采用两供电臂的测量阻抗随过渡电阻的变化轨迹刻画异相短路的阻抗特性,并从理论上对各因素的影响规律进行分析。为简化分析,仅考虑单一影响因素,多影响因素相当于多个单一影响因素的叠加。
3.1 过渡电阻对测量阻抗的影响规律
将式(13)整理为测量阻抗随过渡电阻Zf变化的形式,并忽略供电线,得到
(16)
从式(16)中可以看出,当线路参数和变压器参数确定时,即kα、kβ、ZSα、ZSβ确定时,Zα2、Zβ2与Zf呈线性关系,两供电臂的测量阻抗随过渡电阻的变化轨迹在阻抗平面上为一条直线。直线的斜率项为kα和kβ,由变压器二次侧绕组额定电压的相位差决定;直线的截距项还与变压器等值阻抗和线路等值阻抗有关。
由于Zα2和Zβ2表达式中与Zf无关的项(kαZSβ-kβZSα)互为相反数,因此Zf为零时,即轨迹的起点,关于原点中心对称。
3.2 变压器联结组对测量阻抗的影响规律
我国电气化铁路采用的牵引变压器主要接线方式有Ii、Iii、Vv、Vx、YNd11、YNv、SCOTT七种[20]。其中Ii和Iii为单相变压器,不存在异相短路问题。其余五种变压器可以归纳为Δθ=60°的Vv、Vx、YNd11接线和Δθ=90°的YNv、SCOTT接线这两类。将Δθ=60°和Δθ=90°带入kα、kβ的表达式中,可以得到
(17)
由于认为过渡电阻Zf是纯阻性,因此两供电臂的测量阻抗随过渡电阻的变化轨迹在阻抗平面上的斜率按kα和kβ的辐角旋转得到。也即,Δθ=60°的超前相轨迹与R轴的夹角为-60°,滞后相则为60°;Δθ=90°的超前相轨迹与R轴的夹角为-45°,滞后相则为45°。
同时,由于Δθ=90°的kα和kβ的模值小于Δθ=60°,因此当变压器等值阻抗和线路等值阻抗一定时,Δθ=90°的轨迹起点的模值相比Δθ=60°更小,轨迹与R轴的交点相比Δθ=60°距离原点更近。
3.3 变压器容量对测量阻抗的影响规律
从图4中可以看出,Zsα由ZFSα与ZG串联后与ZRSα并联,再与ZTSα串联组成,变压器等值阻抗ZTSα、ZRSα和ZFSα是Zsα的主要影响因素。变压器等值阻抗与短路阻抗百分比和容量有关,通常电气化铁路牵引变压器的短路阻抗百分比是固定的(通常为10.5%),因此本文主要讨论变压器容量的影响。
Zsα和Zsβ位于式(12)的截距项中,若变压器的容量增大,则Zsα和Zsβ等比例减小,轨迹直线的截距项模值减小,轨迹与R轴的交点更靠近原点;反之若变压器容量减小则轨迹与R轴的交点远离原点。而直线的斜率项不受变压器容量的影响。变压器容量的变化仅改变了直线的起点,不同变压器容量对应的直线互为平移关系。
3.4 牵引负荷对测量阻抗的影响规律
从图5的故障分析电路中可以看出,在考虑牵引负荷时,牵引符合与所在一侧的线路、变压器等并联,故障分析电路由两侧对称变为不对称,牵引负荷对两供电臂测量阻抗的影响不同。从公式上无法得到简洁直观的影响规律,将借助计算和仿真的结果进一步分析。
4 仿真验证
为验证所推导异相短路故障分析电路和测量阻抗表达式的正确性,在基于实时数字仿真仪(Real Time Digital Simulator,RTDS)建立的牵引供电系统仿真平台[21]上测试异相短路故障阻抗,Vx接线牵引变压器、自耦变压器参数和线路长度见表1,牵引网采用5导体模型,参数见文献[22]。

表1 RTDS仿真系统主要参数
在相同的系统参数下,表2为分别用式(13)计算和RTDS平台仿真得到不同过渡电阻下的测量阻抗值。

表2 理论计算与RTDS平台仿真结果 Ω
从表2中可以看出,理论计算与RTDS平台的仿真结果在不同过渡电阻下得到的测量阻抗均相近,证明了所推导异相短路故障分析电路和测量阻抗表达式的正确性。为深入研究异相短路的阻抗特征,以表1所示的供电臂参数为基础,验证并进一步研究过渡电阻、变压器联结组、变压器容量、牵引负荷和供电线长度对阻抗特性的影响规律。
4.1 过渡电阻的影响规律
异相短路的过渡电阻主要由电弧组成,电弧电阻与其长度和电流有关,根据经验其估算公式为[23]
(18)
式中:Rg为电弧电阻;Lg为电弧长度;Ig为电弧电流。
异相短路时电流有数千安,电弧长度为数十厘米到一米多[5-7],根据式(18)估计电弧电阻为数欧姆。取过渡电阻的变化范围为0~5 Ω,并分别取Δθ=60°和Δθ=90°,跟据RTDS仿真的结果,在阻抗平面上绘制两供电臂测量阻抗随过渡电阻的变化轨迹见图6,同一组数据用相同颜色标记,实线和虚线分别代表α相(超前相)和β相(滞后相),阻抗轨迹箭头所指方向过渡电阻增大,相邻两点间过渡电阻相差1 Ω。

图6 不同变压器联结组下测量阻抗随过渡电阻的变化轨迹
从图6中可以看出,两组测量阻抗的轨迹均为直线,其中超前相阻抗轨迹位于第四象限、滞后相轨迹位于第二象限。当过渡电阻为0时,两供电臂轨迹的起点均位于电阻轴附近,分别为5.066-j0.009、-5.066+j0.009、2.925-j0.005、-2.925+j0.005 Ω,关于原点中心对称,符合3.1节中的理论分析。随着过渡电阻的增大,超前相和滞后相的电阻均增大且变化相同;超前相的电抗减小、滞后相的电抗增大且变化的绝对值相同。在阻抗平面中表现为随着过渡电阻的增大,测量阻抗的轨迹向远离R轴方向延伸。
4.2 变压器联结组的影响
对比图6中两组测量阻抗的轨迹可以看出,不同变压器联结组下的轨迹虽均呈直线,但两组轨迹在起点和斜率上均有显著差异。Δθ=60°的变压器轨迹起点分别为5.066-j0.009、-5.066+j0.009 Ω,轨迹与R轴的夹角为60°、-60°;Δθ=90°的变压器轨迹起点分别为2.925-j0.005、-2.925+j0.005 Ω,轨迹与R轴的夹角为45°、-45°。与Δθ=60°相比,过渡电阻为0时,Δθ=90°的测量阻抗模值更小,在阻抗平面中表现为轨迹起点距原点更近。随着过渡电阻的增大,不同变压器联结组的超前相和滞后相电阻均增大,但Δθ=90°变压器的变化量更大;不同变压器连接组的超前相电抗均减小、滞后相电抗均增大,但Δθ=90°变压器的变化量更小,在阻抗平面中表现为轨迹斜率更缓,符合3.2节中的理论分析。不论何种变压器连接组,轨迹的起点均关于原点中心对称、轨迹与R轴的夹角大小相等,符号相反。滞后相和超前相测量阻抗仍分别位于第二、第四象限。
4.3 变压器容量的影响
根据相关标准,电气化铁路牵引变压器的容量范围为10~126 MV·A[24]。在其余条件不变的前提下,跟据RTDS仿真的结果,在阻抗平面上分别绘制不同牵引变压器下两供电臂测量阻抗随过渡电阻的变化轨迹,如图7所示。
从图7(a)中可以看出,当两供电臂变压器容量相等,容量为16、31.5、63 MV·A时阻抗轨迹的起点分别为9.436-j0.028、-9.436+j0.028、5.066-j0.009、-5.066+j0.009、2.424-j0.002、-2.424+j0.002 Ω,均位于R轴附近。相同过渡电阻下,随着变压器容量的增大,超前相的电阻减小、滞后相的电阻增大;超前相和滞后相的电抗几乎没有变化。在阻抗平面中表现为三组轨迹的斜率相同,互为平移关系,平移方向几乎与R轴重合。当变压器容量增大时轨迹向靠近原点的方向平移,而容量减小时向远离原点的方向平移,符合3.3节中的理论分析。
而从图7(b)中可以看出,当两供电臂变压器容量不等时,超前相、滞后相的电阻变化趋势与变压器容量相等时相同;随着滞后相变压器容量的增大,超前相电抗减小、滞后相电抗增大。在阻抗平面中表现为各组轨迹仍具有相同的线形和长度,但平移方向从几乎与R轴重合变为斜向。相比于容量相等时,容量较大那一相的轨迹向R轴正方向斜上方平移,符合3.3节中的理论分析。
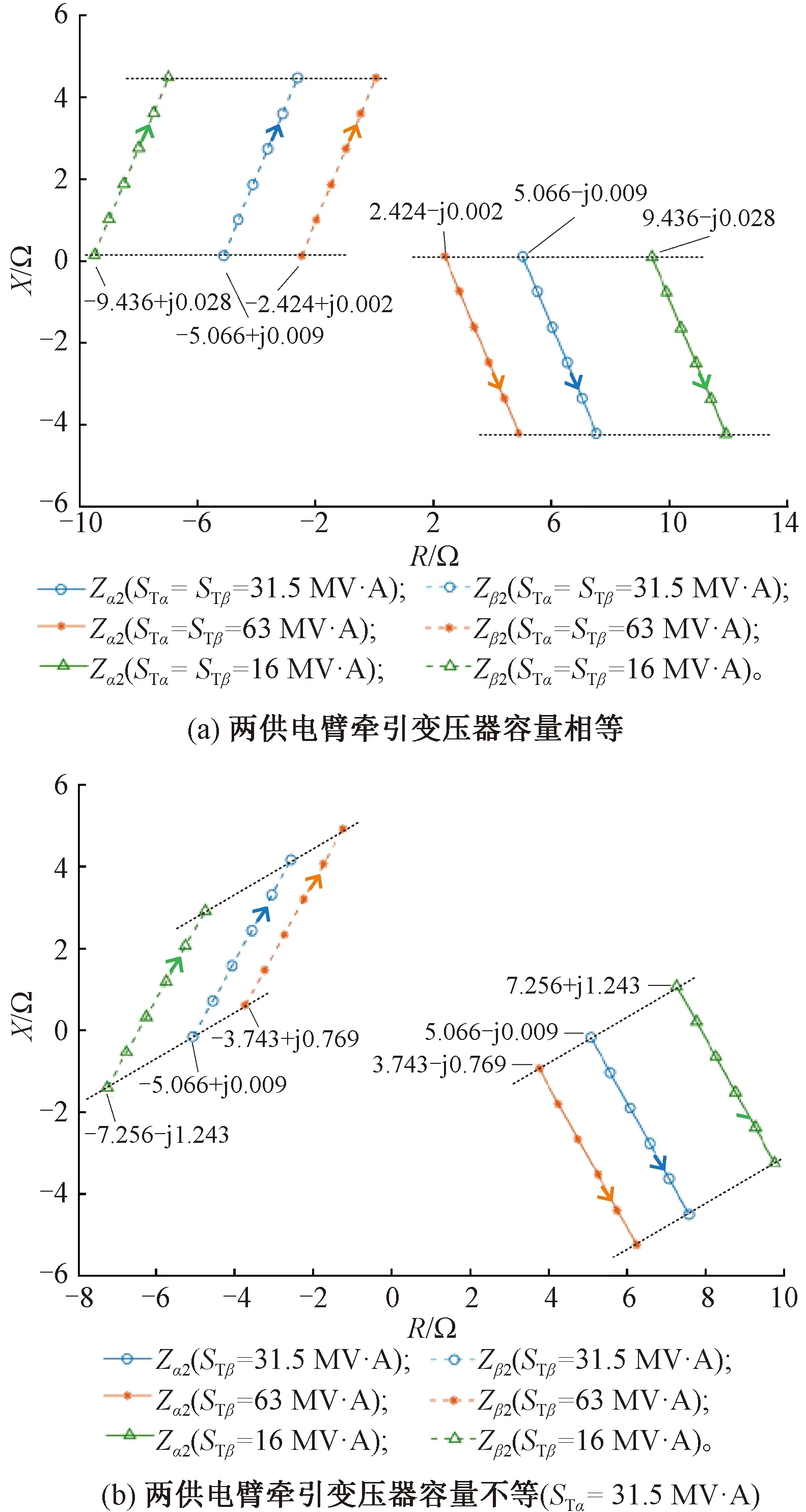
图7 不同变压器容量下的测量阻抗变化轨迹
由于容量相等时两供电臂轨迹的起点位于R轴附近,只要超前相变压器容量大于滞后相,超前相轨迹的起点就将向斜上移动进入第一象限、滞后相轨迹的起点向斜下移动进入第三象限。
4.4 供电线的影响
供电线的长度影响故障侧和非故障侧电流的分布,进而影响阻抗特性。根据RTDS仿真结果,在阻抗平面上分别绘制不同供电线长度下两供电臂测量阻抗随过渡电阻的变化轨迹,见图8。
从图8中可以看出,供电线长度对两供电臂轨迹均有影响。随着供电线长度的增大,超前相和滞后相的电阻电抗随过渡电阻增大而变化的变化量增大。在阻抗平面中表现为随着供电线长度的增大,超前相轨迹的起点向R轴正半轴移动、滞后相轨迹的起点向R轴负半轴移动,轨迹仍保持为直线且斜率不变,但长度变长。滞后相测量阻抗仍位于第二象限,超前相轨迹的起点随着供电线长度增大从第四象限落入第一象限。

图8 不同供电线长度下测量阻抗变化轨迹
4.5 牵引负荷的影响
异相短路故障后电压降落通常不大,列车往往可以继续取流行进,未切除的负荷对测量阻抗产生影响。由于高速铁路动车组的功率因数近似为1,为简化分析将牵引负荷等值为纯电阻,且仅考虑电分相处的那一牵引负荷。根据RTDS仿真结果,在阻抗平面上分别绘制不同牵引负荷在超前相和滞后相时两供电臂测量阻抗随过渡电阻的变化轨迹见图9,图9中负荷阻抗无穷表示无负荷。

图9 不同牵引负荷下的阻抗轨迹
由图9可以看出,牵引负荷对两供电臂的阻抗轨迹均有影响,负荷处在超前相和滞后相的影响不同,负荷所在那一相的阻抗随过渡电阻的变化趋势显著改变。负荷在超前相时,随着负荷等值阻抗的减小,超前相电阻和电抗随过渡电阻增大的变化量减小;负荷等值阻抗一定时,超前相电抗随过渡电阻增大而变化量逐渐减小。负荷在滞后相时,随着负荷等值阻抗的减小,滞后相电阻和电抗随过渡电阻增大的变化量增大;负荷等值阻抗一定时,滞后相电抗随过渡电阻增大而变化量逐渐减小。在阻抗平面中表现为有负荷那一相的轨迹由直线变为向R轴弯曲的曲线,且负荷阻抗越小弯曲程度越大。滞后相和超前相测量阻抗仍分别位于第二、第四象限。
5 结论
在牵引变压器和全并联AT牵引网等值电路的基础上,推导了异相短路故障分析电路和测量阻抗表达式,分析了异相短路阻抗特性、影响因素及多种典型情况下阻抗角的分布,结论如下:
(1)异相短路测量阻抗受过渡电阻、变压器联结组、变压器容量、牵引负荷和供电线长度等因素的影响,本文所推导的异相短路故障分析电路和测量阻抗表达式能用于多参数、多线路、多工况的异相短路故障分析。
(2)不计牵引负荷时,两供电臂测量阻抗随过渡电阻的变化轨迹是一条直线,轨迹的起点关于原点中心对称,轨迹与R轴的夹角大小相等,符号相反。
(3)变压器联结组影响轨迹直线的起点和斜率,变压器容量仅影响轨迹的起点,供电线长度影响轨迹的起点和长度,牵引负荷会使所在相的轨迹向R轴方向弯曲。
(4)当两供电臂变压器容量相等或超前相容量小于滞后相时,两臂测量阻抗分别位于阻抗平面的第二、第四象限;当超前相容量大于滞后相,且过渡电阻较小时,测量阻抗分别于第一、第三象限。
