考虑旅客多维出行需求的动态列车开行方案优化
2022-12-02孙国锋马亚雯
孙国锋,景 云,2,马亚雯
(1.北京交通大学 交通运输学院, 北京 100044; 2.北京交通大学 智慧高铁系统前沿科学中心, 北京 100044;3.中国市政西北设计研究院有限公司,甘肃 兰州 730030)
现阶段高速铁路(以下简称“高铁”)旅客的出行需求呈现多维化,个性化的特点[1]。传统列车开行方案在给定客流总量基础上,决策列车起讫点,开行数量及停站方案等内容[2],较少考虑对旅客出行时刻、旅行时间和票价等需求的响应。因此,有必要根据多维个性化客流需求,研究匹配旅客多维出行需求的动态列车开行方案优化问题。
列车开行方案的研究思路一般基于客流需求总量[3-5]和备选集思想[6-10],编制满足旅客空间位移需求的开行方案。文献[3-5]均采用双层规划方法建立列车开行方案模型。为简化列车开行方案优化问题规模,一些研究预先给定部分变量,在此基础上优化其余变量,例如文献[6]在给定列车停站方案的基础上,优化列车运行路径和客流径路,文献[7]预先给定了列车的起讫站等;还有一些研究采用压缩变量可行域的方法简化问题,如文献[8]在生成备选开行列车集合基础上研究列车开行方案问题。在求解策略方面,文献[3-5]均设计了启发式求解方法,而在运用备选集思想简化问题后,也可以使用多项式算法求解列车开行方案问题,如列生成算法[6]、拉格朗日松弛算法[8]等。上述研究较少考虑旅客时间需求,导致列车开行方案难以满足多维旅客出行需求。
近年来,也有学者在研究列车开行方案问题中考虑了客流时变需求[11-14]。文献[11]考虑旅客出行时变需求,在列车开行方案中引入时间要素,得到了匹配时变需求的列车开行方案;文献[12]在传统列车开行方案中增加了列车始发时间的估计值,运用双层规划方法研究了面向服务水平的高铁列车开行方案优化问题;文献[13]在研究城际高铁开行方案中引入了客流出行时间信息,基于时空网络构建了开行方案优化模型,对客流时变特征明显的城际铁路列车开行方案进行了研究。虽然部分研究将旅客的时变需求引入列车开行方案问题中,但未考虑旅客出行需求与列车开行方案之间互相反馈的影响关系,未系统的考虑旅客多维度出行需求对列车开行方案问题的影响。
不同于传统列车开行方案优化问题,本文考虑了出行时刻、旅行时间、票价等旅客需求,引入动态列车开行方案概念,在传统开行方案决策变量基础上,优化列车的始发时刻。
1 动态列车开行方案的内涵
1.1 动态列车开行方案定义
列车开行方案在较长的时间周期中(1年或2年)是静态不变的,仅在新编列车运行图之前进行微调。然而,随着高铁旅客出行需求的个性化发展,应当考虑旅客的出行选择行为,动态优化列车开行方案。因此,动态列车开行方案是指,以满足旅客出行需求为目标,确定起讫站、停站方案、开行数量等静态指标及出发时刻、列车等级、票价等影响乘客出行选择行为的动态指标。
传统的列车开行方案问题一般是以OD客流量为驱动,决策开行方案静态指标[15],在客流分配过程中不考虑旅客出行选择行为。动态列车开行方案在考虑旅客选择行为的基础上,动态分配客流,优化列车始发时刻等动态指标,与开行方案-运行图协同优化问题的区别在于动态列车开行方案优化不考虑运行线冲突消解问题。
1.2 动态列车开行方案优化问题描述
沿高铁列车运行方向,车站集合为U={1,2,3,…,m},m为车站数,车站u∈U由列车始发终到候选车站和非始发终到候选车站两类组成,见图1。
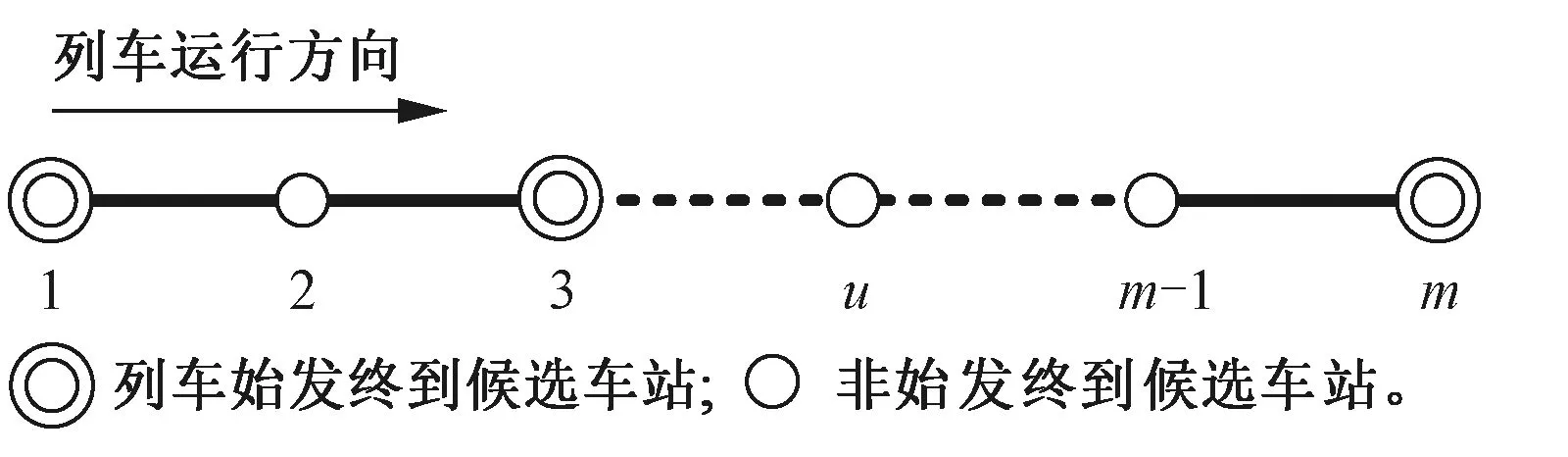
图1 高铁线路示意
本文提出考虑旅客多维出行需求的动态列车开行方案优化,主要研究思路为:首先,基于高铁线路的最小列车追踪时间值,生成研究时段内可行开行列车备选集合。然后,以备选开行列车集合为输入,基于时空网络构建动态列车开行方案优化问题模型;模型的输入为路网信息、备选列车信息、旅客需求信息;目标函数为系统效用最大化;决策变量为列车选择开行弧段变量和客流分配变量;模型输出为列车开行和客流分配方案,其中列车开行方案包括开行列车对数、每列车的发车时刻、列车停站。最后,设计基于模拟退火算法框架的求解算法,并以实际案例验证模型和算法的有效性。
在建立模型时,重点围绕旅客需求与动态开行方案之间的关系进行优化,因此需要对高铁运输服务过程中的影响因素进行假设:
(1)列车的所有席位为二等座。
(2)所有列车均采用固定编组的方式,并且列车的定员一致。
(3)计算列车在区间运行时间时,只考虑区间纯运行时分,不考虑起停车附加时分[16]。
(4)在优化动态列车开行方案中,假设各车站候车能力和到发线能力充足。
1.3 符号说明
动态列车开行方案优化模型的相关集合、索引、参数和变量见表1。

表1 集合、索引、参数和变量
2 旅客多维出行需求及时空网络
2.1 多维旅客出行需求分析
影响旅客出行选择行为的主要因素包括旅行时间、期望出发时刻和票价等。基于旅客出行选择的3个需求属性,在效用函数中考虑3个影响因素,分别是旅行时间Tn,i,旅客期望出行时间偏差πn,i和票价Fn,i。则旅客群体n选择列车i的效用函数μn,i为
μn,i=α1Tn,i+α2πn,i+Fn,i
(1)

(2)
MNL模型通常会高估或错误分配重新选择概率,而广义吸引模型(Generalized Attraction Model,GAM)可以有效解决该问题[17],准确描述旅客对列车的选择行为。
在GAM中,wn,i为列车i∈I对旅客群体n的影子吸引力,则旅客群体n选择任列车i∈I′的概率pn,i为
(3)
(4)
根据式(4)可更准确描述高铁旅客的决策过程。
2.2 时空网络构建
利用时空网络描述动态列车开行方案优化问题,时空网络有向图为G=(H,A)。(u,s)∈H表示时间坐标为s、空间坐标为u的节点,弧(u,v,s,t)∈A表示在s时刻从节点u出发至t时刻到达节点v的路径。
时空网络构建过程见图2,包含2类弧段,分别为运行弧和停站弧。其中运行弧是连接相邻两车站顶点之间的弧段;停站弧是连接同一车站节点不同时刻之间的弧段。列车对时空网络弧段占用形成了完整的列车时空路径,可描述列车在各站的到发时刻及停站方案。

图2 时空网络示意
3 模型建立
3.1 目标函数
综合考虑企业运营收益和旅客出行需求,以系统的整体效用最大为目标,从最大化高铁运输收益、最小化旅客总旅行时间损失和期望出发时间偏差等3方面来构造目标函数。目标函数为
(ω1Fn,i-ω2α1Tn,i-ω3α2πn,i)
(5)
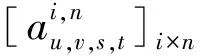
(6)

(7)
3.2 约束条件
(1)列车流平衡约束

(8)
(2)列车始发终到车站约束
列车必须从始发、终到候选集合中选择始发车站和终到车站
(9)
(3)客流分配约束
对同一时段内相同起讫点的客流进行合并,形成旅客群体。每个旅客群体最多只能选择一列高铁列车出行。
(10)
(11)
(4)客流平衡约束
任意旅客群体只能在一个时空节点上车或者下车,则客流平衡约束为
∀(u,s)∈V
(12)
(13)
(14)
(15)
(5)列车能力约束
列车所分配的旅客数量不得超过列车的额定载客能力,即
(16)
(6)开行列车数量约束[13]
模型的目标函数主要考虑旅客多维出行需求,可能会造成开行列车数量越多,目标函数越好的情况。因此,在保证旅客服务质量的同时,为了减少高速铁路企业的运营成本,应对列车开行数量进行约束
Num(Ω)≤Nummax
(17)
(7)安全间隔约束
列车在始发站的出发时刻必须满足安全出发间隔。约束为
(18)
(8)变量约束为
(19)
(20)
(21)
(22)
4 算法设计
本文构建的非线性整数规划模型为NP-hard问题,很难在多项式时间内求解,元启发式算法对求解该类问题具有很好的效果,作为元启发式算法之一的模拟退火算法被多次运用求解列车开行方案问题[11,13-14,18]。因此,本文结合问题特点,基于模拟退火算法框架设计求解算法。
运用模拟退火算法求解动态列车开行方案问题的思路如下:生成由停站方案、列车在始发站发车时刻、客流分配三部分组成的初始解;通过设计删除列车、拆分列车、超出上座率客流调整、未分配客流重新分配等方法生成邻域解;在内层循环中,分别设计随机交换停站信息和合并开行列车策略,若产生新解优于当前解,则用新解替换当前解,否则,按给定的概率随机替换当前解;在算法外层,保存算法历史最优解;当满足算法终止条件时算法结束,得到动态开行方案最优解。
4.1 初始解的生成
(1)解的表达形式
动态列车开行方案初始解的构成包括列车开行解和客流分配解两部分,即问题的解Ω为
(23)
(24)
式中:Ti为列车i的开行解,由停站方案和列车发车时刻组成;Pi为分配给列车i的客流。STi为列车i的停站,表示列车在沿途各车站的停站弧占用情况,取值为0或1;DTi为列车i的发车时刻,表示列车i在始发站占用列车运行弧的情况。由于列车在各区间的运行时分和停站时长已知,可通过式(24)确定列车在各站的到发时刻。
(2)基于贪心算法的初始解生成方法
在生成初始解的过程中,客流分配解采用贪心算法生成,在客流分配解的基础上,根据分配客流的始发终到车站需求,生成列车开行解。客流分配解生成的方法如下。
遍历长度为m的旅客群体列表,每次选择一个未分配的旅客群体进行分配,遍历旅客群体的期望出发时间序列,将该旅客群体分配给期望出发时间偏差最小的列车,执行m次迭代后将返回的结果作为客流分配的初始结果。具体流程如下:
Step1初始化。初始化客流分配列表,生成n行m列取值为0的二维初始客流分配列表。
Step2基于贪心算法生成客流分配列表。
生活中,我们可以有意制造这样的机会。比如:当孩子请你帮他做一件事时,你可以告诉他:“妈妈还有事,五分钟后能帮你,你可以等一会吗?”当孩子问你问题时,你不妨说:“这个问题很有意思,让妈妈想一下,你也再思考下,五分钟后我们来交换答案好吗?”当孩子渴望立即得到回应,兴奋地要跟你讲一件事时,如果你正在忙,大可不必停下手中事转向他,而是可以让他稍作等待。
for 每个旅客群体n∈N
初始化旅客群体n的期望出发时间偏差列表。
for 每列车i∈I
计算期望出发时间偏差πn,i,将旅客群体n对每列车的期望出发时间偏差添加到期望出发时间偏差列表中。
Step3计算旅客群体n的期望出发时间偏差列表中的最小值。
Step4将最小值对应索引处的客流分配结果由0改为1。
Step5通过贪心算法可生成期望出发时间偏差值相对较好的客流分配初始解,合并列车开行初始解和客流分配初始解便可生成动态列车开行方案问题的初始解。
4.2 邻域解的生成
动态列车开行方案生成邻域解,需要同时考虑列车开行解和客流分配解,生成策略主要包括:停开列车、拆分列车、超出上座率阈值的客流分配调整、未分配客流重新分配。
(1)停开列车和拆分列车[13]
检查每列车在各区间的上座率,若某列车在各区间的上座率均小于规定停开列车阈值,则停开该列车。若某列车在某区间的上座率小于规定拆分列车阈值,对列车进行拆分,停开低于阈值区间的列车,更新拆分列车后新列车在始发站的发车时刻。
(2)调整超出上座率阈值的客流分配
检查每列车在各弧段的上座率,如果列车在某弧段的上座率大于上座率阈值,首先计算超出上座率阈值的客流数量;然后随机搜索上座率小于上座率阈值的列车,按照期望出发时间偏差由大到小将超出客流在客流分配列表中的值由1改为0,直至所有弧段上座率满足列车能力约束。
(3)未分配客流重新分配
当停开列车、拆分列车及调整超出上座率阈值的客流分配后,可能存在未分配的客流,重新分配该部分客流,直至所有客流均被分配。
首先遍历未分配旅客n∈N,判断旅客群体n的出行需求弧段;然后遍历列车开行列表,如果列车i的开行弧段满足旅客群体n的出行需求弧段,并且该弧段上座率小于上座率规定阈值,则将旅客群体n分配至列车i;最后检查所有旅客是否全部分配,如果还有旅客未被分配,则采用贪心算法,增开列车,直至所有未被分配旅客均分配完毕。
4.3 适应度函数及内层合并列车操作
(1)适应度函数
解Ω的适应度函数为
fitness(Ω)=Z(Ω)-Λ·Num(Ω)
(25)
式中:fitness(Ω)为当前解Ω对应的适应度函数;Z(Ω)为当前解Ω的目标函数值;Λ为开行列车惩罚系数;Num(Ω)为当前解Ω的开行列车数量。
(2)合并列车操作
首先在列车开行解中随机生成需要合并的列车i_num_col,然后在i_num_col±10范围内随机生成需要合并的另一列车,判断生成的两列车是否均开行。如果不是,重新执行该步骤,直至生成均开行列车的两行解;如果是,则对生成的两行解进行合并,将原本分配给两列车的客流重新分配给合并后的列车。计算合并后新解在各区间的客座率,对超出客座率的客流重新分配,分配过程为:计算每列车在各区间的平均客座率,如果当前平均客座率大于0且小于阈值L,则将当前客流分配给该列车,遍历所有列车后,若还存在未分配客流,增开列车,直至所有客流全部被分配。
4.4 基于模拟退火的算法步骤
模拟退火算法,需要设置初始温度、温度下降规则、同温度下迭代次数、终止规则等参数。温度下降规则选择给定降温系数下降方式;同一温度下的迭代次数使用最大迭代次数进行控制;算法终止规则使用当前温度低于给定的终止温度。算法步骤如下:
Step1初始化。初始化初始温度为Γ0,终止温度为Γe,退火步长,允许接受概率为初始化初始解为Ω0。

Step3当前温度Γ>Γe,执行内层算法:
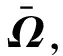


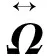
Step5温度下降,Γ=Γ×,返回Step3。

5 案例分析
5.1 基础数据
北京北—呼和浩特东高铁,运营里程为459 km,沿线共设车站16个。根据线路结构特点及现有列车开行模式,由于沙河站和旗下营南站客流极少,故暂不考虑这两个车站。考虑到北京北和清河站的动车段配属在清河,两个车站的旅客出行需求相似,可将北京北站和清河站合并为清河站,客流需求数据也相应合并处理。共13个车站,车站编号依次为1~13,线路和车站信息见图3,区间运行时分信息通过列车运行图获得。
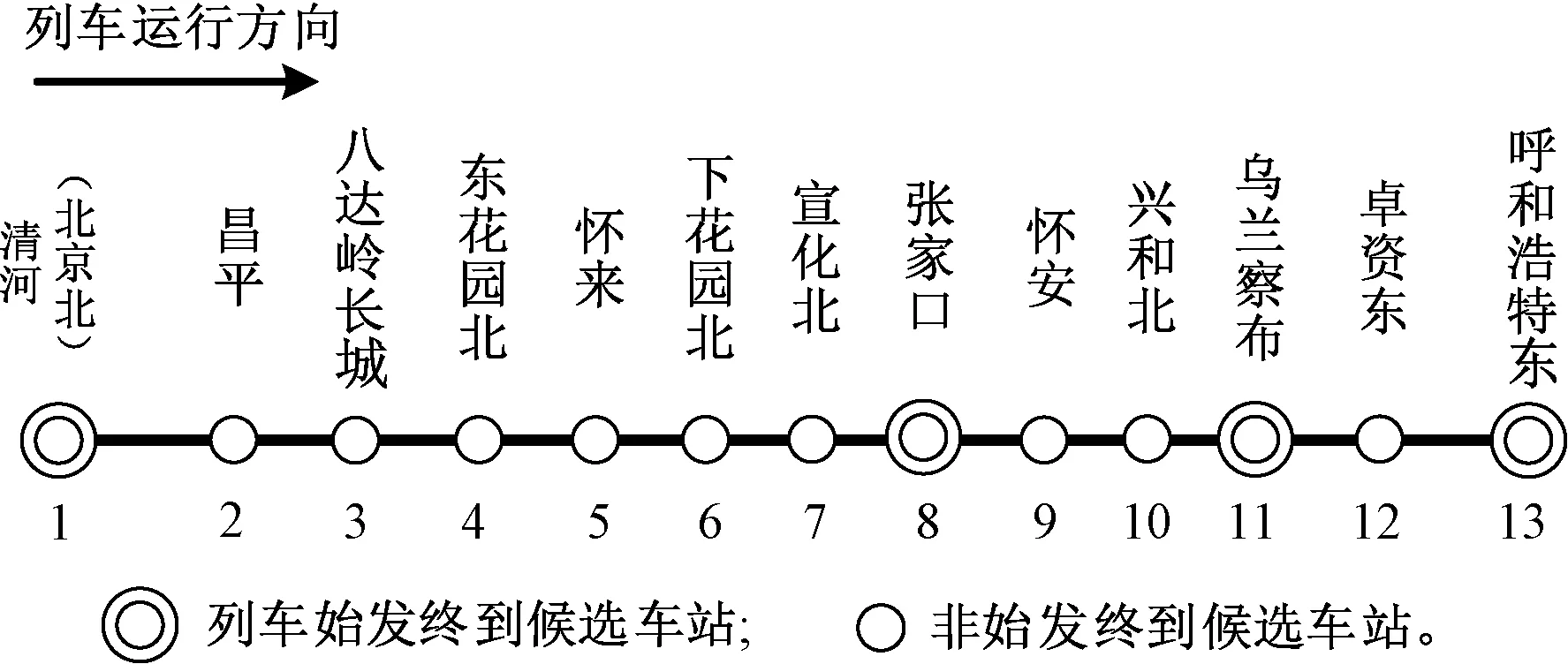
图3 清河(北京北)—呼和浩特东间区间和车站信息
按照2021年某日客流优化动态列车开行方案,总客流为23 790人,由于篇幅有限,未详细列举各OD的客流信息。依据现行开行方案随机生成某时间段旅客出发时刻需求。为了减少问题计算规模,对同一时段内相同起讫点的客流进行合并,形成旅客群体共计793组。

算法中相关参数取值分别为:Γ0=100;Γe=0.1;=0.9;邻域解生成过程中,允许删除列车阈值为0.10;允许拆分列车阈值为0.18;适应度函数中,Λ=1 000;合并列车操作中,L=0.75。
5.2 优化结果分析
(1)动态开行方案结果分析
动态列车开行方案见图4,图中圆圈表示列车在该站停车,列车开行数量共计28列,列车起讫点和开行数量见表2。

图4 清河(北京北)—呼和浩特东动态列车开行方案

表2 优化前后列车起讫点和开行数量对比 列
优化后开行列车总对数共计减少2列。优化前全部开行清河(北京北)—呼和浩特东的长程列车,优化后除开行长程列车外,还增开清河(北京北)—张家口/乌兰察布的短程列车,满足旅客出行需求。
优化前后各个车站经过的列车数、停站列车数对比情况如图5所示。图中横坐标为各车站序号,左侧纵坐标为停站列车数,右侧纵坐标为经停比。优化前后开行列车及停站方案综合对比情况见表3。

图5 各车站列车停站情况

表3 优化前后列车开行及停站对比
表3中的停站总数包含列车在始发终到站的停站次数。优化后开行列车数量减少了6.67%,列车停站总数减少了14.94%;优化后得到的动态列车开行方案在满足旅客多维需求的同时,减少了列车开行对数和停站次数,有效降低高速铁路运营成本。
优化后开行方案在各区间的客座率见图6。所有列车的平均客座率为51.14%;列车在各区间的客座率比较均衡,客流分配结果满足列车能力约束。
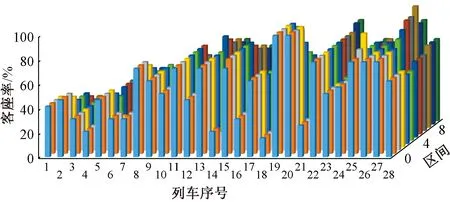
图6 各区间列车客座率
(2)优化目标结果分析
目标函数及各部分的数值随迭代次数的变化规律,如图7所示。随着迭代次数的增加,目标函数整体呈现增长趋势,旅客群体总旅行时间损失和期望出发时间偏差呈现递减趋势。

图7 目标函数及各部分的数值随迭代次数的变化规律
为了进一步验证模型的正确性和适用性,对可变参数ω1、ω2和ω3取不同值的计算结果进行分析,得到动态列车开行方案统计指标见表4。表中客票收益、总旅行时间损失、期望出发时间偏差均为基于旅客群体选择概率的计算结果。当ω1的取值增加时,考虑旅客群体选择概率的系统客票收益呈递增趋势,ω2和ω3取不同值的计算结果也具有相似的特征。符合动态列车开行方案的优化目标。
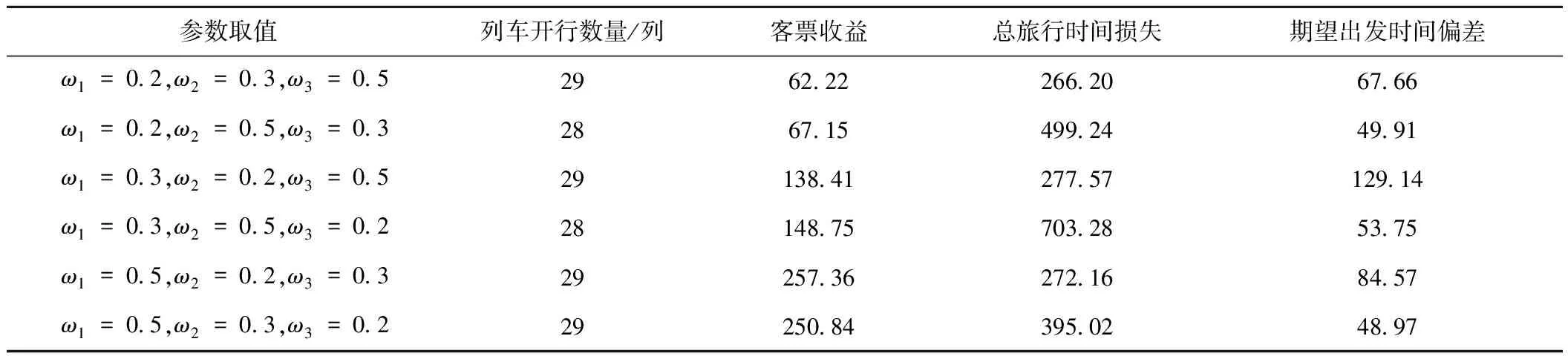
表4 不同参数取值下动态列车开行方案统计指标
(3)计算效率分析
算法在PyCharm 2021平台使用Python语言实现,运行环境为1台CPU Intel i7-5500U,4 GB内存的计算机,当ω1、ω2和ω3取不同参数值时,算法平均计算时间约为3.6 h。ω1=0.3,ω2=0.4,ω3=0.3时算法收敛迭代过程如图8所示,算法迭代至35代时收敛。本文设计的求解算法整体收敛性良好,能有效求解动态列车开行方案优化问题。

图8 算法收敛迭代图
6 结论
本文引入广义吸引力模型描述旅客出行选择行为,构建开行方案时空网络,将旅客对列车的选择概率嵌入目标函数,建立基于旅客多维出行需求的动态列车开行方案优化模型,以铁路运营企业和旅客系统最优为目标,考虑列车流平衡约束、始发终到站约束、客流分配约束、客流平衡约束、列车能力约束、列车开行数量约束、发车安全间隔约束,设计模拟退火算法进行求解。实例计算结果表明,本文所构建的列车开行方案模型与算法能设计考虑旅客出行选择行为的开行方案,优化列车出发时刻等动态指标,响应旅客多维出行需求,为面向市场导向的高铁开行方案制定提供决策支撑。
在未来的研究中,将进一步考虑路网条件下动态列车开行方案优化问题,设计更加高效的算法求解动态开行方案优化问题。
