基于3D图像的机车机器人闸瓦尺寸算法研究

沈云波，王俊平，张慧源，袁宏翔，李淼成，陈胜蓝，江海啸

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

刹车系统正常平稳工作是列车安全运行的重要保障。列车在制动过程中，闸瓦因与列车轮对发生摩擦而产生损耗。为了保证行车安全，当闸瓦磨耗达到一定程度时，需人工进行尺寸复核；如果确实达到磨耗极限，则需及时进行更换。由于全国运营列车数量较多，采用人工的方法检测闸瓦，需要耗费较多的人力和财力，同时还需要停车检测。

图像检测技术目前已经被广泛应用于对目标对象的识别和测量。文献［1］研究了2D机器视觉技术在铁路货车闸瓦检测中的应用，在图像拍摄效果较好的前提下，算法稳定性、重复性较好。文献［2］建立了基于GS-SIFT特征描述子的列车闸瓦螺栓丢失识别方法，对待测图像与模板图像进行特征匹配，提高了算法的适应性。文献［3］研究了货车运行过程中获得闸瓦图像的识别、磨耗的自动检测方法，该方法识别率高、鲁棒性好，能满足实际检测要求。文献［4］在实验室对BGA芯片进行了测量实验，根据测量相关数据计算了BGA芯片的引线间距、球形引线半径、共面性等参数，该文所述方法也可以用于其他存在共面性问题的表面测量，应用场景广泛。文献［5］结合特征值法和随机采样一致性（random sample consensus，RANSAC）算法，剔除了异常值，与传统的方法相比，该方法能很好地适应异常值情况，鲁棒性好。文献［6］基于欧氏聚类方法进行了改进，同时研究了去畸变的三维激光雷达点云方法，能自动更正距离阈值，快速准确地检测障碍物。文献［7］对大规模点云使用哈希表进行编码，同时通过八叉树的空间划分，提了一种工件余量快速求取方法，实现了对工件余量的快速求取，有效地提高了搜索效率。文献［8］提出了使用最小二乘曲线拟合进行点云滤波，能获得准确的地形点，对于地形比较复杂的城市区域尤其斜坡地区有良好的滤波效果。

目前使用3D技术进行列车关键零部件检测的算法尚不多见。3D图像数据相比2D图像数据多了一维深度的信息，且在识别准确度上，3D图像算法相比2D图像算法更具优势，因此采用3D技术进行列车关键零部件检测，更容易实现对复杂环境工况（例如灰尘多、反光导致点云数据缺失、光滑表面镜像、点云数据的不均匀采样、遮挡等）下零部件的准确测量。

针对机车车辆复杂的运行与检修环境，本文提出一种基于3D图像的机车机器人闸瓦尺寸算法，其通过设计一些3D算子，在点云存在缺失、噪点、成片虚假点云的条件下，可实现高效测量，具备一定的算法鲁棒性，能较大程度地减少人工现场测量工作量。

1 闸瓦尺寸检测算法

本文处理的三维点云为3D传感器输出的有序点云。点云获取设备扫描机车闸瓦时，点云组成包括刹车盘、闸瓦、闸瓦固定支架及其他环境干扰。其他环境干扰主要包括噪点、刹车盘（刹车盘与闸瓦长期摩擦）镜面反射及反光的虚假倒影点云和虚假倾斜点云。对于闸瓦检测而言，刹车盘、闸瓦、闸瓦固定支架及其他环境干扰点云等属于背景点云，对目前尺寸检测会产生一定的干扰，并且会降低检测精度。

机车在进行库外检修时，闸瓦与刹车盘通常处于贴紧状态，基本没有间隙，这种情况被定义为抱闸；在进行库内检修时，闸瓦与刹车盘通常处于松开状态（1～3 mm间隙），这种情况被定义为松闸。由于机车检修不一定严格按照规范要求停车，有时候也会根据人工经验，导致存在库内检修时出现抱闸或者库外检修时出现松闸的情况。

因此，闸瓦尺寸检测时，对大量背景点云的滤除及本身边缘的提取、基准选择及尺寸检测提出了很高的要求，同时需要考虑抱闸与松闸车辆。图1示出拍摄的松闸2D与3D点云，图2示出拍摄的抱闸2D与3D点云。

图1 松闸点云数据Fig.1 Pine gate point cloud data

图2 抱闸点云数据Fig.2 Hold point cloud data

在进行闸瓦尺寸检测之前，本文首先采用Voxel‐Grid体素滤波器［9］对点云进行下采样处理，以提高点云处理速度。闸瓦尺寸检测算法主要包括感兴趣区域（region of interest，ROI）定位、高效去飞点滤波、背景滤除、边界跟踪及尺寸测量等。算法架构如图3所示。

图3 算法流程Fig.3 Algorithm flowchart

1.1 ROI定位算法

为了更精确地测量闸瓦尺寸，本文设计了3种ROI以相互配合使用（图4）。其中，1号为基准ROI，主要用于尺寸测量基准的计算；2号为测量ROI，主要用于尺寸测量；3号为滤波基准ROI，主要用于背景滤除。

图4 ROI选取Fig.4 ROI selection

受现场地沟施工精度、控制算法及编码器等因素影响，机车机器人在同一位置、同一动作前后采集的点云数据存在一定的定位偏差。在进行模板标注阶段，标注软件选取的模板ROI与实际检测点云ROI存在一定的偏差；为了减少ROI偏差导致的测量误差，需要对ROI进行区域定位。ROI定位算法包括相机成像和点云配准基础算法，流程大致如下：

（1）基础算法

特征点P在世界坐标系中的坐标（Xw，Yw，Zw）与相机坐标系中的坐标（Xc，Yc，Zc）之间的变换关系［10］为

式中：R——世界坐标系Qw-XwYwZw变换到相机坐标系Qc-XcYcZc的旋转矩阵。

R是正交矩阵，自由度为3。R的具体表达式为

式中：ϕ，θ，φ——3个旋转角度。

T为世界坐标系Qw-XwYwZw变换到相机坐标系Qc-XcYcZc的平移向量，其表达式为

旋转矩阵R和平移向量T总共包含有6个参数，这6个参数被称为外部参数。

三维空间中的点到二维平面中的点之间的成像几何变换可以利用透视投影模型表示［11］。相机坐标系中的点P（Xc，Yc，Zc）与图像坐标系中的点p（x，y）之间的变换关系可以通过相似三角形得到，具体如下：

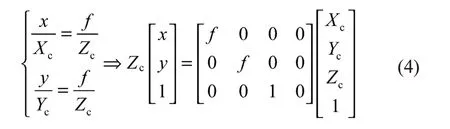
式中：f——镜头的焦距。

假设图像坐标系的原点位于像素坐标系（u0，v0）位置，则图像坐标（x，y）和像素坐标（u，v）的关系如下：

式中：dx，dy——单个像素点在x轴和y轴方向上的物理尺寸。

综合式（1）～式（5），可得世界坐标（Xw，Yw，Zw）与像素坐标（u，v）之间的变换关系：

式中：fx，fv，u0和v0——相机的4个内部参数，其中fx=——相机的成像矩阵。

迭代最近点算法（iterative closest point，ICP）属于经典的点云配准算法，同时也是目前使用最广泛的点云配准算法之一，其主要通过欧式变换求解源点云到目标点云的旋转与平移矩阵。P=｛pi（xi，yi，zi）|i=1，2，3，…，aa｝为源点云，Q=｛qi（xi，yi，zi）|i=1，2，3，…，aa｝为目标点云。式（7）是目标函数，迭代求取最优变换矩阵可被转换成求取min[ ]f(R，t)的最优解（R，t），R和t分别是源点云到目标点云的旋转和平移矩阵。

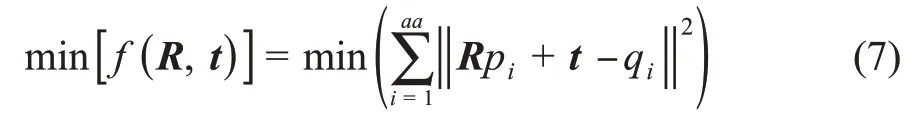
目前，经典ICP算法需要粗配准，同时满足“距离足够近”这一条件之后才能进行精确配准；但在点云存在噪点时，容易陷入局部最优解。随着配准算法研究的不断深入，目前出现了一些全局3D点云配准算法，能在一定程度上弥补经典ICP算法的不足。

文献［12］通过求取源点云和目标点云的曲率特征，不需要进行初配准，实现了点云全局配准。文献［13］通过计算源点云和目标点云的积分体积特征，求解变换矩阵。文献［14］通过构建源点云和目标点云的特征直方图作为特征描述子来求解变换矩阵。文献［15］使用RANSAC方法对源点云和目标点云进行配准，使用四点法构造点云的稀疏点对，效率较高。文献［16］提出Go-ICP全局匹配算法，该算法主要基于分支定界算法，验证了变换矩阵的全局最优性，但Go-ICP需要结合DT算法，耗时较长。本文主要使用文献［15］提出的点云配准算法，并兼顾一定的耗时效率。

（2）坐标转换

假设通过点云配准算法获取的源点云到目标点云的最佳旋转与平移矩阵为（R，t），则源点云（XS，YS，ZS）转换到目标点云坐标系下的公式为

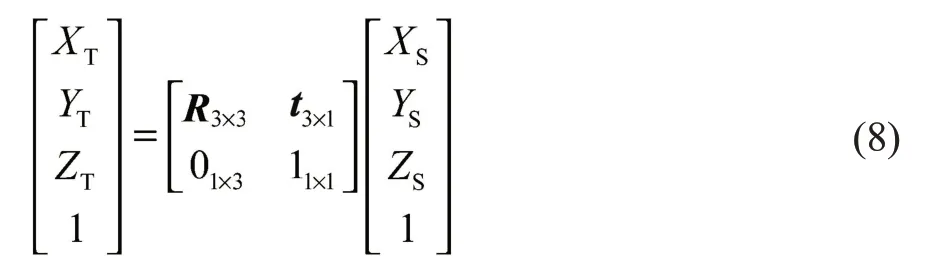
为了将源ROI转换成目标ROI以提高定位偏差，需要进行ROI边界点转换。

（3）ROI边界点转换

为进行ROI边界点转换，如图5所示，首先假设源点云ROI区域的A，B，C，D这4个顶点的2D坐标为（Au，Av），（Bu，Bv），（Cu，Cv），（Du，Dv），通过有序点云2D和3D一一对应关系，获取A，B，C，D的3D坐标，即（XAS，YAS，ZAS），（XBS，YBS，ZBS），（XCS，YCS，ZCS），（XDS，YDS，ZDS）。

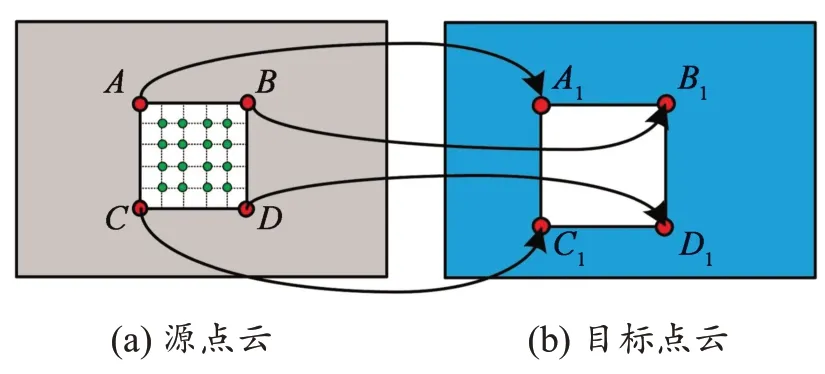
图5 ROI区域定位算法Fig.5 Region of ROI algorithm

将源点云4个3D顶点坐标代入式（8），获取4个顶点在目标点云坐标系下的坐标（XAT，YAT，ZAT），（XBT，YBT，ZBT），（XCT，YCT，ZCT），（XDT，YDT，ZDT）。

假设式（6）中R和T为单位向量，此时相机坐标系和世界坐标系重合，将源点云在目标点云坐标系的4个顶点（XAT，YAT，ZAT），（XBT，YBT，ZBT），（XCT，YCT，ZCT）和（XDT，YDT，ZDT）代入式（6），即可求出源点云ROI 4个顶点A，B，C，D在目标点云图像中的坐标位置A1，B1，C1，D1。

1.2 高效去飞点滤波

针对松闸车辆以及点云遮挡、反光和镜面反射等因素产生的噪点，本文使用有序点云噪点滤除方法，在保证滤波效率的同时，初步分离部分刹车盘和闸瓦之间的噪点，以减少噪点对测量精度产生的影响。

如图6所示，LROI/WRDI分别为有序点云2D检测ROI内的长和宽，bbb（图中红色点）为当前ROI从上往下以及从左往右索引的当前点，a1，a2，a3，…，acc（图中绿色点）为当前点bbb邻域内的点，size为当前点bbb的邻域区域长度，d1，d2，d3，…，dcc为a1，a2，a3，…，acc与当前点bbb的空间距离。

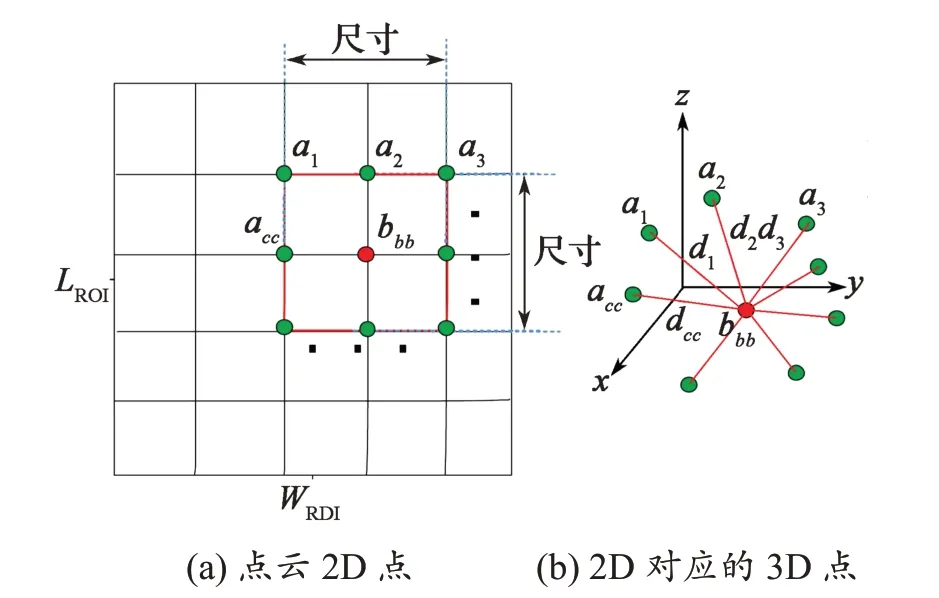
图6 有序点云邻域分析Fig.6 Neighborhood analysis of ordered point cloud

自适应噪点去除算法具体如下：

（1）在ROI内从上往下、从左往右地索引当前点，并假设此时当前点为by。

首先，计算每个当前点by的邻域距离d1，d2，d3，…，dx。当前点by的坐标为（xy，yy，zy），当前邻域点ax的空间坐标为（xx，yx，zx），如果当前邻域点ax-1无效，则不进行邻域距离计算，继续搜索另一个邻域点ax。

接着，计算当前所有邻域点的平均距离并作为当前点的特征距离。将特征距离记为Dy，则有

然后，循环ROI内的所有点，得到ROI内y个点的特征距离D1，D2，D3，…，Dy。

最后，对特征距离进行均值和方差计算：

D y＜(-s1×σ)，表明点云与邻域距离较短，局部点云密集，闸瓦与刹车盘交界边缘处曲率较大，容易产生密集点云。在该处设置阈值，可以有效去除密集点云噪点。

D y＞(+s2×σ)，表明点云与邻域距离较长，局部点云稀疏，不同的车辆（运行年限、运行路况）闸瓦差异较大，反光、镜面反射差异、松闸度随机等因素导致闸瓦与刹车盘交界边缘点云间距比较随机，同时容易产生稀疏点云。在该处设置阈值，可以有效去除稀疏点云噪点，达到初步去噪效果。

图7示出松闸状态下滤波前后闸瓦点云数据情况。图7（a）为松闸状态下原始点云数据；图7（b）中白色点云为刹车片点云以及由刹车片反光、镜像等产生的组合噪声点云。通过有序点云噪点滤除方法，滤除了部分松闸状态下的边缘背景点云。

图7 松闸状态下滤波前后闸瓦点云数据Fig.7 Point cloud data of brake shoe before and after filtering under release

1.3 背景滤除算法

背景滤除算法主要实现刹车盘与闸瓦基准面之间的闸瓦侧面点云提取，可以排除部分背景点云，包括刹车盘点云、闸瓦上表面点云、闸瓦固定支架点云、光滑刹车片反射的闸瓦垂直虚假点云、光滑刹车片反射的闸瓦倾斜虚假点云及区域内的噪点等。

将通过ROI定位算法转换后的滤波基准ROI定义为TargetROI-3，基准ROI定义为TargetROI-1。背景滤除算法包括RANSAC方法［5］、平面拟合等一些基础算法，流程大致如下：

（1）基础算法

RANSAC原理是采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。RANSAC算法的基本假设是数据中包含正确数据（内点）和异常数据（局外点），当给定一组正确的数据（很少的抽样数据）时，计算出符合这些数据模型的参数，使这个模型满足点到平面的距离足够小的内点数量最多。

假设点集P由q个空间点p（xj，yj，zj）（j=1，2，3，…，q）组成，针对初步拟定的模型（例如直线或抛物线），建立点集P的超定方程组A T=B，其中T为待求的变量；根据点集P，可以计算出矩阵A与向量B。T可以采用最小二乘法计算，当点集P存在异常噪点时，若直接求取超定方程组参数T，则可能会存在较大的误差。

RANSAC在计算参数T的过程中考虑了异常噪点的影响，首先从给定的点集P中随机选出不重复的o（o＜q）个点，组合成点集Q；根据最小二乘法求解建立点集Q的超定方程组CT=D，根据点集Q可以计算出矩阵A与向量B；最后，将拟合出来的参数t应用到整个点集P，根据阈值ε区分模型的内点和外点。重复多次上述操作，直至挑选出包含内点集Po最多的模型。

假设点集P由o个空间点p（xi，yi，zi）（i=1，2，3，…，n）组成，待拟合的平面如下：

式（13）中，a，b，c，d为平面方程系数。平面拟合类似于求解系数a，b，c，d，使式（14）所示距离之和最小：

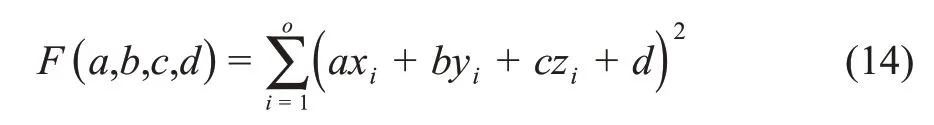
假设点集P的中心坐标为

由于P中o个空间点p（xi，yi，zi）（i=1，2，3，…，o）同时满足式（13），可得

假设所有点的平均距离为xˉ，将式（13）与式（16）相减，可得

再假设

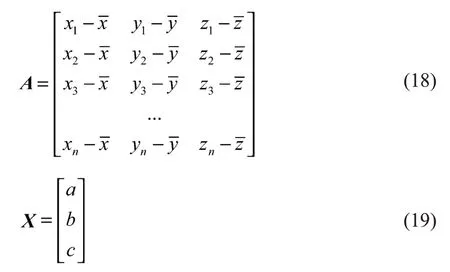
则式（17）可被写成

如果平面上的点都理想化地在同一平面上，不存在平面外的噪点，那么式（17）完全成立，实际情况下，由于三维噪点的存在，平面拟合的目的是求取（20）的最小值。

对矩阵A进行奇异值分解：

式中：V——3×3正交矩阵；U——o×o正交矩阵；Σ——o×3的对角矩阵。

结合式（18）、式（19）和式（21），可得

式（22）中，VTX是列矩阵，并且当且仅当VTX=［0 0…1］T时，式（22）取得最小值，及式（20）取最小值，此时有

式（20）中，AX=0最优解为X=（a，b，c）=（vo1，vo2，vo3），将该解代入式（16），可以求得d，最终完成平面系数的求解。通过对A进行奇异值分解（singular value decomposition，SVD），平面拟合的系数就是最小奇异值对应的特征向量。

带局外点的平面拟合，主要通过设置距离阈值、置信度和局外点比例，计算点到平面的距离，以剔除局外点并拟合内点数据，从而获得三维平面的解析表达式。图8所示为利用抗干扰平面拟合算法获得内点和外点的效果。

图8 抗干扰平面拟合算法Fig.8 Anti-interference plane fitting algorithm

（2）平面滤波

首先对TargetROI-1与TargetROI-3中的有效点云分别进行鲁棒性平面拟合。假设两个拟合平面plane1和plane2的平面方程分别为

同时假设测量ROI（TargetROI-2）内有效点云数目为e，e个点云坐标集分别为｛（x21，y21，z21），（x22，y22，z22），…，（x2e，y2e，z2o）｝，获取e个点中满足式（26）的点云，这些点云即为测量ROI（TargetROI-2）中的点云，它们位于plane1和plane2之间。

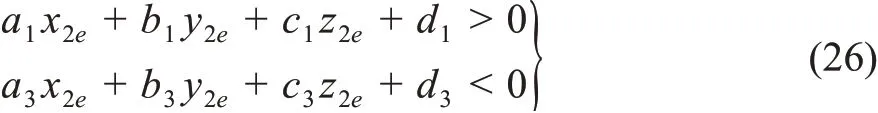
图9示出平面初步滤波效果示意，其中绿色点云为两平面中间的点云，红色点云为其他点云。显然，对于光滑刹车片反射的闸瓦倾斜倒影虚假点云，由于倾斜点云与刹车片紧密相连，这些虚假点云使用式（26）无法被滤除，会直接影响测量效果。

图9 平面初步滤波Fig.9 Planar preliminary filtering

闸瓦与刹车盘之间可能有0～3 mm松紧度间隙，如图10所示。

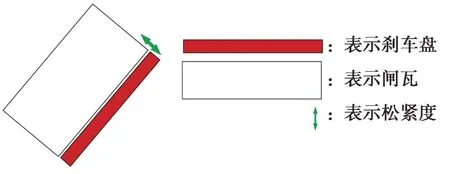
图10 闸瓦与刹车盘接触形式Fig.10 Contact form between brake shoe and brake disc

为了解决上述的闸瓦边界提取困难问题，对式（26）进行改进：

满足（27）的点云为位于plane1上方及位于plane2下方2 mm外的点云。图11示出虚假点云滤除效果，显然闸瓦下边缘已经和倾斜虚假点云分开，有效滤除了刹车盘点云、闸瓦上表面点云、闸瓦固定支架点云、光滑刹车片反射的闸瓦竖直虚假点云等。

图11 虚假点云滤除效果Fig.11 False point cloud filtering effect

（3）下边缘初步获取

将平面滤波后的点云映射到2D图像中，如图12（a）所示，然后进行2D最大连通域分析，结果显示小区域非目标点云被有效去除，如图12（b）所示。

图12 最大连通域分析前后2D图像Fig.12 Effects before and after maximum connected domain analysis

获取2D最大连通域下边缘信息，所得闸瓦的2D下边缘点分别为a1，a2，a3，…，an，如图13所示。n个点对应三维点云坐标依次为｛（x1，y1，z1），（x2，y2，z2），…，（xn，yn，zn）｝。

图13 闸瓦下边缘点Fig.13 Lower edge of brake shoe

1.4 边界跟踪

由于闸瓦松紧度存在一定的随机性，同时刹车盘不是一个绝对理想的平面，长时间灰尘堆积、油渍及不均匀磨耗等因素会使平面度出现一定的误差。采用1.3节所示方法进行处理，初步获取闸瓦下边缘。当松闸间隙大于2 mm时，获取的闸瓦下边缘较准确；但松闸间隙小于2 mm时，闸瓦与刹车盘的点云会粘连在一起，会对检测精度产生一定的影响。为了解决小间隙的误差问题，本文增加了边界跟踪算法，其包括点云法向量基础算法，具体流程如下：

（1）基础算法

目前点云法向量主要有3种类型估计方法：第1种是基于Delaunay三角分割方法，但是针对现场采集的有噪点的点云数据，该方法不是很适合；第2种是基于统计的学习方法，该方法计算比较复杂，不适合在大规模点云处理或者实时性要求较高的工业场景中；第3种是基于局部表面拟合法，其耗时短、效率高。本文主要采用第3种拟合方法。

基于局部表面拟合方法，其近似于估计表面一点的相切面的法向量。假设平面方程为

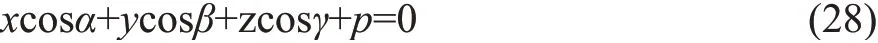
式中：cosα，cosβ，cosγ——平面上点（x，y，z）处法向量的余弦值；|p|——原点到平面的距离。

求解平面方程，其可转换成求解式（13）中a，b，c，d这4个参数，其中a2+b2+c2=1。点云的法向量可被表示为（a，b，c）。

（2）边界跟踪算法

如图14所示，ak为闸瓦下边缘点，m为当前点ak的邻域区域长/宽，tk1，tk2，tk3，…，tk（m2-1）为ak不包含本身的邻域点。图15示出闸瓦边缘点ak上下的邻域点。

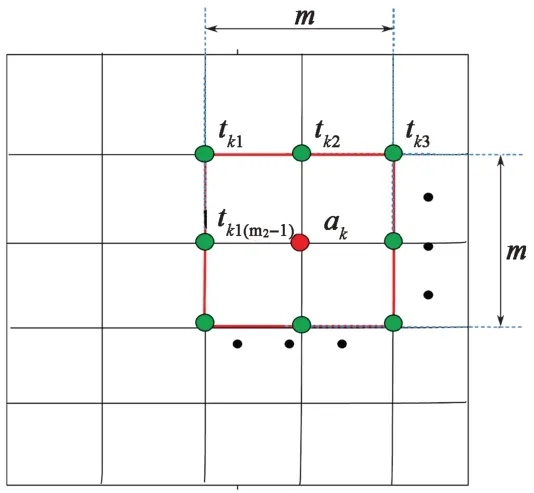
图14 闸瓦下边缘邻域点Fig.14 Brake shoe lower edge point field point

图15 闸瓦边缘上下邻域点Fig.15 Brake shoe edge up and down field point

由于拍摄的点云噪点较多，同时闸瓦侧面并非理想光滑面，长时间灰尘堆积及油渍会使闸瓦侧面产生部分凹凸不平现象。为了避免法向量突变影响边缘跟踪效果，本文采用加权法向量的方法。假设m=3，ak的第p个邻域点为tkp，p∈（1，2，…，8），tkp对应的法向量为（nkpx，nkpy，nkpz），此时定义ak的加权法向量为（Nkx，Nky，Nkz），并按照式（29）进行计算。

ak的4个邻域角点被赋予权重，最近的上下左右4个邻域点被赋予权重1并进行加权平均，以保证法向量不会随着m值的增加而增加；同时减少噪点或闸瓦侧面凹凸不平导致的法向量突变对检测精度的影响。

下面介绍闸瓦边界跟踪流程（图16）。

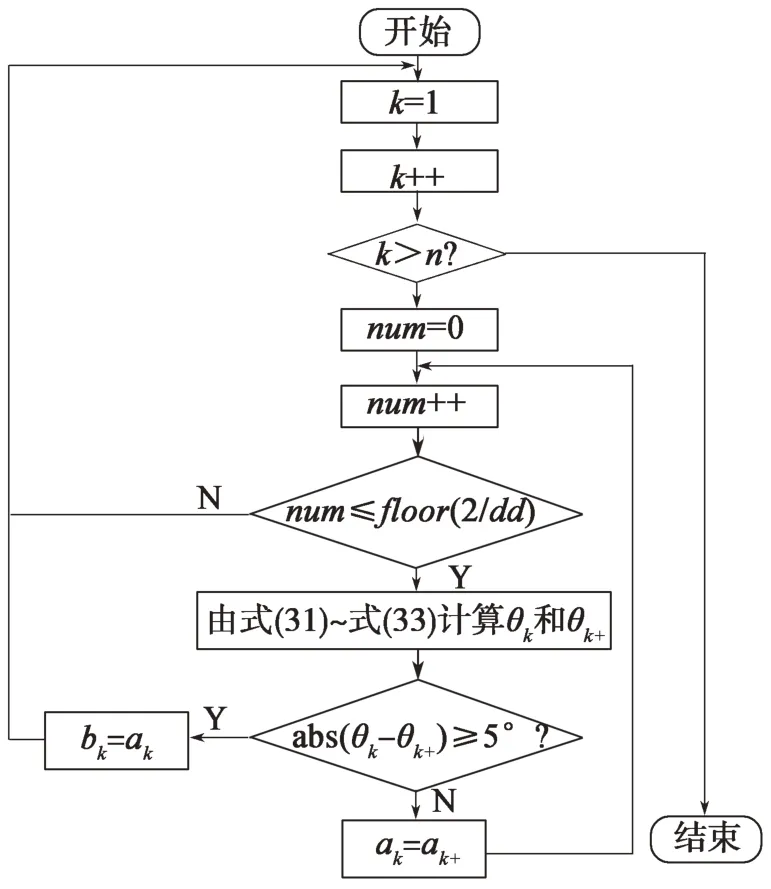
图16 闸瓦边界跟踪流程Fig.16 Flow chart of brake shoe boundary tracking

步骤1：初始化k（k=1），当前闸瓦边缘点从0开始跟踪；初始化bi，bi=0（i=1，2，…，n），bi表示闸瓦下边缘点ak下一步的跟踪点。

步骤2：k++，当前闸瓦边缘点ak替换为相邻下一边缘点。如果k＞n，进入步骤7，否则进入步骤3，n为闸瓦边缘点跟踪前的数目。

步骤3：num=0，初始化迭代次数num。

步骤4：num++，迭代次数加1。如果num≤floor（2/dd），进入步骤5，否则进入步骤2，dd为平均相邻最近点云间距，由于1.3节中分离的闸瓦与刹车盘间隙为2 mm，因此最大迭代次数num为floor（2/dd），最接近终止迭代条件。

步骤5：计算上下两个有效法向量的夹角θk和θk+，进入步骤6。假设ak的上下邻域点（同一列最近上下邻域点）为ak-和ak+，a1，a2，a3，…，an上下邻域点如图15所示，假设ak-的有效法向量为（Nkx-，Nky-，Nkz-），ak+的有效法向量为（Nkx+，Nky+，Nkz+），上下两个有效法向量的夹角θk和θk+的计算公式如下：

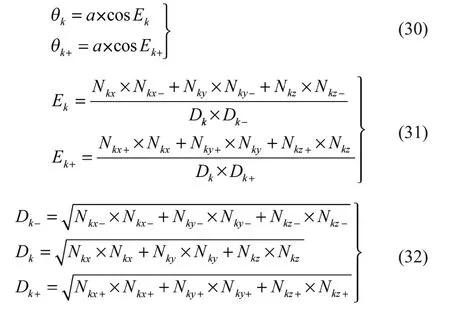
步骤6：如果满足夹角阈值条件，即

则赋值bk=ak，当前闸瓦边缘点ak赋值给最后跟踪的点bk，同时进入步骤2；如果不满足阈值条件，则ak=ak+，当前边缘点替换为同一列最近下邻域点ak+，同时进入步骤4。

步骤7：统计bi（i=1，2，…，n）中不为零的元素，将不为零的元素插入Bi（i=1，2，…，tt）中，Bi为最后跟踪的第i个边缘点，tt为最后不为零的元素个数。

边界跟踪效果如图17所示。

图17 边界跟踪闸瓦下边缘点Fig.17 Boundary tracking brake shoe lower edge point

图18示出不同虚假点云跟踪效果，绿色点云为满足式（29）的点云，蓝色点云为最终边缘点的提取效果。可以看出，对于绿色和蓝色这两种虚假点云，都能很好地进行边缘提取，具备较强的鲁棒性。

图18 虚假点云跟踪效果Fig.18 False point cloud tracking effect

1.5 闸瓦厚度测量

第1.3节中背景滤除算法计算的基准ROI平面方程为a1x+b1y+c1z+d1=0，闸瓦边缘点对应三维点云坐标依次为（x1，y1，z1），（x2，y2，z2），…，（xtt，ytt，ztt），由点到平面的方程为

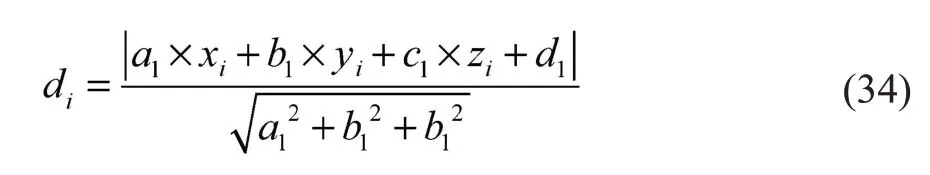
计算出边缘点闸瓦厚度值di（i=1，2，…，tt），再将di进行排序，为了排除可能出现的异常点，去掉值较小的10%元素，去掉后为Di（i=1，2，…，tt），选取Di中值最小的元素作为闸瓦磨耗值，其中t为去除值较小的10%元素后剩余90%的数值个数。

2 实验验证

为了验证算法的效果，使用怀化机务段采集的70张不同形态、位置、光照等场景下的闸瓦图片数据进行了试验验证。具体图像场景示例如图19所示。

图19 闸瓦不同场景示例图Fig.19 Sample diagram of brake shoe scene

图20示出闸瓦厚度检测精度对比，其中测量值通过现场测量得到，算法检测值通过执行算法得到，绝对误差为测量值与算法检测值的绝对误差值。可以看出，对于测试的70张闸瓦的图像，测量值与算法检测值的误差大部分在1 mm以内。虽然在采集的闸瓦图像中存在大量噪声和虚假点云，且这些噪声数据与真实闸瓦数据粘连严重，但是通过算法处理，可以去除噪声。同时光照明暗对算法精度基本没有影响，尽管2D图像在视觉上较难找到闸瓦的位置，但是算法依然能够准确地测量闸瓦的厚度。

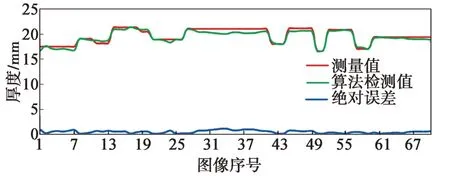
图20 闸瓦厚度检测精度对比Fig.20 Comparison of measuring precision of brake shoe thickness

本文针对目前采集的不同形态数据，添加了高斯噪点进行鲁棒性分析，期望值为0，标准差分别为1、2、3，并将3种高斯噪点结果取平均值，对检测精度与鲁棒性进行验证，结果如图21所示。可以看到，除了个别精度有一定的降低，整体精度大部分被控制在1 mm以内，验证了该算法具备较好的鲁棒性。

图21 高斯噪点闸瓦厚度检测精度对比Fig.21 Comparison of measuring percisions of brake shoe thickness at gauss noise point

3 结语

针对机车车辆复杂的运行与检修环境，本文提出了一种基于图像的机车机器人闸瓦尺寸算法，并设计了一些3D算子，能在点云存在缺失、噪点、成片虚假点云条件下，实现高效测量。其首先实现模板ROI与测量ROI区域的变换，一定程度上弥补机车机器人的重复定位误差；对基准ROI进行平面拟合，以弥补反光造成的点云缺失、噪点的影响；使用高效滤除算法，滤除部分刹车盘与闸瓦之间的点云；针对边缘区分难度大的问题，针对性地设计滤波算子，初步分离闸瓦边缘；使用基于梯度的边缘提取与跟踪算法，实现闸瓦点云边界精确提取；最后使用排序策略的统计学方法，实现较准确的尺寸测量，具备一定的算法鲁棒性。本文创新性地设计了3D算子，并成功应用于影响列车行车安全的闸瓦尺寸测量，能极大程度减少人工现场测量工作。由于闸瓦成像千变万化，本文考虑的复杂场景还有待进一步完善，后期需要根据现场更加复杂的环境设计兼容性更强的算子。