问题导向 开放探究 助力思维*——“点与圆上的点的最值问题”微专题复习

张 超

(江苏省苏州工业园区东沙湖实验中学，215021)

初三数学二轮复习,旨在从“碎片化”的基础知识系统复习向重难点专题突破过渡.微专题是对专题复习的有效补充.在备考过程中,教师若能将知识“化零为整”,分割成若干个微专题给学生进行专项突破,往往能够达到“小身材,大能量”的教学效果.疫情期间,笔者在线上开设了一节市级初三中考复习研讨课,深度融合信息技术的课堂,以问题为导向,促进学生开放探究,为了提升学生的数学思维能力.本文以“点与圆上的点的最值问题”微专题复习为例,谈谈自己的一些见解.

一、设计流程与思考

1.确立主题方法提炼

提出问题:平面内,点P到圆上一点的距离最长为6,最短为2,求圆的半径?

学生活动:动手画图,通过画线段,测量线段长度等方式,学生历经动手操作,形成猜想,尝试说理的过程.

方法提炼

根据三角形三边关系可知:

|OA-OB|≤AB≤OA+OB, 当O,A,B三点共线时等号成立.

设计意图确立本节课研究主题——点与圆上的点的最值问题.利用分类的思想,找到图1,图2两个基本图形,同时完成对上述问题的猜想的验证.揭示平面内一点与圆上一动点最值问题的原理,方法的提炼为解决此类问题提供了思维的路径.

2.联想突破方法巩固

问题1如图3,Rt∆ABC,AB⊥BC,AB=6,BC=4,以AB为直径的半圆交AC于点D,P是弧BD上一个动点,连结CP.求CP的最小值?

问题2如图4,点P坐标(3,4),圆P的半径为2,B为x轴上任意一点,A是线段OB中点,点M是圆P上的动点,点C是线段MB的中点.求AC的取值范围?

问题3如图5,在平面直角坐标系xOy中,设点P(m,n)是以点C(1,4)为圆心,1为半径的圆上一动点,二次函数y=x2-1的图像与x轴相交于A,B两点.求PA2+PB2的最大值?

设计意图问题1是让学生结合具体图形套用方法.后面两个问题都涉及转化思想,其中问题2是利用中点构造三角形中位线进行转化,而问题3是通过坐标表示线段长度实现转化.低起点、有梯度的问题探究使得学生的思维螺旋上升,并激发了探究的兴趣.

方法巩固的三个问题,体现找寻连圆心、画线段、求距离的基本套路.问题2和问题3都没有直接指向点与圆上的点的最值.让学生结合题设条件产生合情、合理的联想实现转化成为解题的关键.对问题2,由图形中A,C两点是中点,学生联想到中位线,连结OM,实现转化.问题3的目标导向,由线段平方的和,让学生联想到勾股定理,通过点P(m,n)表示出PA2+PB2=2(m2+n2)+2,再由“数”的表示引导学生对应到“形”,学生顺势联想到线段OP2,最终转化为点与圆上的点的最值问题.以问题为导向,通过对题设条件的“聚焦”,帮助学生积累“联想”的经验.

3.多元表征方法应用

问题4如图6,在∆ABC中,∠ACB=90°,BC=6,AC=8,D是AC的中点,P是BC上的一个动点,将∆DCP沿DP所在的直线翻折得到∆DC′P.你能提出哪些问题?

变式现将∆ABC绕顶点C旋转α°(0°≤α≤360°)形成∆A′B′C,如图7所示,M是A′B'的中点,连结BM.求BM的取值范围.

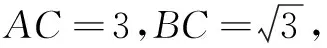
变式如图9,点P在Rt∆ABC内部,满足∠PAB=∠PBC,连结BP.求CP最小值.

设计意图从显圆到隐圆的过渡,让学生找出与上述探究问题的“同”与“不同”.问题4和问题5开放性探究的设置,让学生自主去发现问题、提出问题并且尝试解决问题.学生在圆的多元表征下追寻动点的运动踪迹、画出动点的运动路径(圆)、应用已有方法解决与隐圆相关的线段最值问题.

学生历经对图形信息的直观想象、数学抽象、逻辑推理等过程,从发现隐性圆,到类比探究,再到实现了知识的串联,从而提高了问题意识.问题4及其变式,展示图形翻折与旋转.问题5及其变式,通过动点P的位置变化,让学生探求到动态过程中隐藏着相等的数量关系(线段、角度).在圆的多元表征下,从不同的问题背景中抽象出点圆最值的基本图形,提高学生解决问题的能力.

4.揭示模型回溯本源

问题6回顾上述探究过程,你能找到哪些隐圆模型?

学生活动:独立思考后各小组学生合作交流,指定组内代表发言.

师生相互补充,共同归纳出图10——13四种常见隐圆模型.

设计意图本节课不仅在于学生掌握点与圆上的点的最值问题的解题策略,更重要的是领悟数量关系和几何图形的对应,形成轨迹意识.隐圆也只是探究的个例,所隐的也不仅限于圆,也可以是线段、双曲线….具体到本节课,圆只是解决此类问题的工具,当揭示模型,化隐为显时,学生利用几何直观,迅速识别问题本源——点与圆上的点的最值.

二、 教学立意的阐释

1.基于问题导向,技术助力教学

探究始于问题,问题在哪里?联想、推广、因果互逆思考、寻求关联等,都是发现问题的良策.方法巩固阶段,针对问题目标的间接性,设置有梯度的问题串,因果互逆,鼓励学生展开联想,寻求问题的突破;方法应用阶段,在圆的多元表征下,依据动态问题中数量关系的变与不变,确立寻模型——现隐圆——明路径——解最值的基本思路,放手课堂,学生自主去发现、提出、分析、解决问题.

课堂中融合信息技术,实现高效教学.课前,借助易加学院、教师云端备课、前学发布研究问题,让学生先行思考、带着问题进入课堂.共学指向课堂练习,由学生在线作答,再由数据跟踪分析,能精准诊断课堂教学效果.延学用作课后拓展,引用与本专题相关的微课,促学生课后自主探究.腾讯会议的互动批注功能,能实时呈现课堂中师生的互动探究.进一步，还可以借用几何画板来呈现动点轨迹.线上教学限于知识难易程度、学习环境等方面的制约,学生很难长时间专注,而腾讯会议的录屏功能,可以让学生可以循环学习,从而打破课堂时间、空间的壁垒.运用信息技术服务线上教学、互动学习、多项感官体验,提升学生学习的兴趣的同时,实现了课堂的高效．

2.基于多元变式,驱动思维发展

点圆最值相关问题是近年中考热门问题,也是学生易于丢分、难以理解的问题.如果仅仅停留在就题论题,不利于理解问题的本质,学生也难以体会不同问题之间的关联.为突破这一瓶颈,课堂中以问题1为切入口,套用方法,重在解其理.问题2和问题3是对点圆最值问题的变式探究,借助题设条件,转化问题目标,找到基本图形,实现得其法.问题4和问题5及其变式,经历有圆到无圆、显圆到隐圆的过程,让学生充分感受到数与形的对应,并感受悟其道.

数学思维的发展需要学生对问题反复、持续进行探究.本节课探究的生长点是圆的多元表征.在问题的设问中,学生体会到直观感知——操作猜想——逻辑推理——演绎计算四步骤的解题策略.低起点、多维度、深层次的变式教学,让他们感悟思想方法、提升数学思维.

3.基于微专题探究,致力素养形成

微专题教学的本质是“为迁移而教”,且帮助学生实现知识的迁移需要塑造良好的认知结构.因而,微专题教学既要重视学生原有的知识经验、贴合学生思维最近发展区设计问题,又要激发联想、梳理思路、提炼方法、构建解决这一类问题清晰的“路线图”.回顾本节微专题的教学设计,包含显性和隐性两条教学主线.问题教学是显线,即通过问题提出、合作探究、找寻基本图形、提炼解题方法,使学生获得解决此类问题的知识与技能.数学思维能力的提升和学科素养的培养是隐线,即用问题驱动教学、探究引领课堂,让学生历经问题提出——方法提炼——方法巩固——方法应用四个过程.以环环相扣的问题线索激发联想,从而推动学生建构关于本专题的知识结构、方法逻辑,实现得一法、会一类、通一片的目的.

三、微专题复习的实施小结与教学建议

1.切口小,方法精,注重理解

中考二轮复习注重知识的综合运用,因而学生专项知识能力的培养尤为重要.以知识、方法和题型为主题的大专题,由于知识点分布面广,且综合运用性强,学生的理解往往缺乏关联性和整体性.若将一个大专题分割成若干个微专题供学生专项探究,有利于促进学生的理解和对知识的整体建构.微专题的设计,既入口小,又指向明确.如本课中微专题的指向就是平面内的点与圆上的点的线段最值.贯穿课堂始终的主题是,引导学生依据基本图形、提炼解题方法、理解这一类问题的本质.

2.重过程,通思维,培养能力

微专题教学适用于问题教学,即通过问题导向、例题精讲、方法指引、变式应用四个方面推动课堂教学.设置什么样的问题引入、选择什么类型的例题进行精讲、例题精讲是否就是就题讲题、学生在微专题的学习中获得哪些思想方法，这些都是设计时需要认真考虑的方面.

寻找基本图形、提炼解题方法、理解点与圆上的点的产生最值问题的原理,是本课教学的重点也是难点.精讲问题1到问题5,从直接方法套用到转化问题目标,甚至是问题串的设计,学生始终在教师指导下围绕核心问题展开探究.每个问题解决后,学生对解题方法的总结与反思，可以促进他们自然语言、数学语言、图形语言之间的自由转换.因此,微专题的复习的侧重点是课堂中过程性的探究和生成,既要构建清晰的思考路径和知识结构,又要注重学生关键能力的培养.