厚竹叶面积预测模型研究
2022-12-01胡姝珍陈永镇李思卓施建敏
胡姝珍,陈永镇,巫 娟,刘 上,李思卓,施建敏★
(1.江西农业大学·林学院,江西 南昌330045;2.江西省竹子种质资源与利用重点实验室,江西 南昌330045)
厚竹(Phyllostachys edulis‘Pachyloen’),于2008年获批为毛竹(Phyllostachys edulis)新品种[1],于2018年被评定为国家林木良种。厚竹的秆壁特厚,上部近实心,生物量大,竹材冲击韧性良好[2-3],纤维含量高[4],竹笋营养丰富,蛋白质、人体必需氨基酸、Vc 等含量高,单宁含量低[5],可食率高,具有重要的种质研究意义和综合开发利用价值。
叶片是植物光合的重要器官[6-7],而叶面积是研究植物生长、水分拦截、能量交换、光截留、光合效率等的关键变量[8-12]。竹叶因有泡状细胞分布,离体后极易脱水而发生卷曲,为此,叶面积测量过程中需复水使叶面平整,测量困难[13]。加之厚竹叶片比毛竹叶片小,常规叶面积测量方法如称量法、方格法或运用叶面积检测仪、扫描仪等测量叶面积[14-16]误差大。
毛竹叶面积预测模型[17]利用叶长、叶宽与实际叶面积3 个指标通过拟合建立叶面积线性预测模型,以减少叶面积测量产生的误差,该模型在毛竹、淡竹(Ph. glauca)等散生竹和孝顺竹(Bambusa multiplex)等丛生竹[17-19]的叶面积测量上均取得了优良的效果。基于毛竹叶面积预测模型,本研究旨在建立厚竹叶面积的快速、准确、无损测量模型,达到省时省力的目的,为相关基础研究和社会生产实践提供技术支撑。
1 材料与方法
1.1 试验材料
供试厚竹叶片采自江西农业大学竹类植物种质园内(28°45′44″ N,115°50′14″ E),海拔52 m,该竹类植物种质园日照充足,四季分明,年均温度17.1℃~17.8℃,年均降水量1 550~1 650 mm,土壤为红壤。2019 年7 月,于样地内随机选择8 株无病虫害、生长状态良好的2 度厚竹,每株于各冠层、各方位共随机采集40 片叶形完整、状态良好的叶片,密封袋保湿存用。样品合计320 片,2021 年9 月随机选取80%(256片)的叶片进行模型的建立,剩下20%(64 片)的叶片留作模型精度与可行性检测使用。
1.2 研究方法
1.2.1 叶片测量分类
测定每片厚竹叶片的长、宽时,由叶片尖端至叶基部之间的垂直距离为长,以x1表示;两侧叶缘间垂直中脉的最宽距离为宽,以x2表示。采用聚类分析法对叶的长宽比进行分类划分叶型。
1.2.2 叶片扫描法
将多片厚竹叶进行编号,并将刻度尺以与之互不相接的状态依次整齐摆放在扫描仪上,设定图片的分辨率为600 dpi 并进行扫描后,将所得图像传入软件Image J 进行解析,得到各厚竹叶的实际面积。
1.2.3 叶面积仪法
使用CID-203 型叶面积仪,将每片厚竹叶匀速拉出,读取叶面积仪所测面积数值并记录。
1.2.4 叶面积预测建模
随机选择所测样本叶片的80%(256 片)进行建模,剩余20%(64 片)的叶子则用以进行模型的检测。本研究通过将叶长与叶宽的比值导入SPSS 25.0 进行K-值聚类分析,再根据计算结果对叶片形状进行划分,随后将分类后的叶片数据及其实际面积在Excel 2016 中开展分类模型的拟合,从而计算出叶面积线性拟合模型参数并得出最终的拟合模型。
1.3 数据处理
运用均方根误差(RMSE)、残差平方和(SSE)以及预测精度检测模型的误差范围和拟合精度,并解析残差情况(公式1)。以上数据均用Excel 2016 与SPSS 22.0 处理,运用Origin 2019b 作图。
均方根误差残差、残差平方和以及预测精度检测模型计算公式如下:
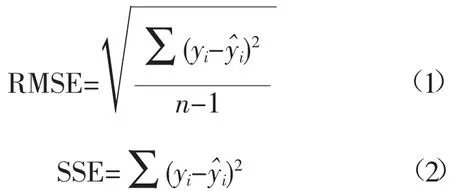
精度检测模型=
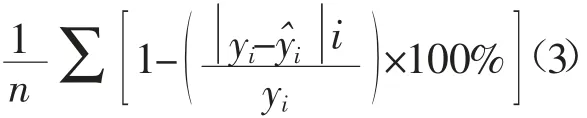
式(1)、式(2)、式(3)中,yi为实测值;i为预测值;n为样本数;RMSE 与SSE 的理想值为0,预测精度理想值为1。
2 结果与分析
2.1 叶片形态分类
将厚竹样本的长宽的比值进行K-值聚类分析,把所有样本分为3 类,分别为:长宽比≤7.38、7.38<长宽比≤8.58、8.58<长宽比(表1)。
2.2 叶面积预测模型构建
根据表1 的聚类分析结果,本研究将256 片厚竹叶以叶片长宽积以及扫描所得实际面积进行整体拟合(式4)和分类拟合(式5),建立拟合方程如下:

式(4)、式(5)中y表示分类拟合叶片面积,x1表示叶长,x2表示叶宽。
图1 是两种拟合方式(图a 为分类拟合、图b 为整体拟合)所得面积和叶面积仪测量所得面积(c)与实际叶面积的R2值比较:分类拟合的R2值最大(0.96),整体拟合的R2值略低(0.95),叶面积仪的R2值最小(0.89),分类拟合所得结果精确度最高,相比整体拟合提高1.36%,比叶面积仪提高8.52%。
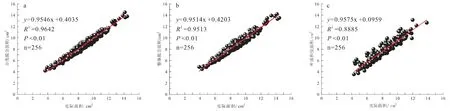
图1 厚竹实际面积与各测量方式拟合度Fig. 1 The fitting degree of the actual area of Ph. edulis‘Pachyloen’with each measurement method
2.3 模型比较
3 种测定方法的误差统计结果如表2 所示,分析可得:分类拟合得到的RMSE 值、SSE 值均为最小,分别是0.40、39.88。此外,其预测精度也最高,达95.94%,相对于整体拟合的95.39%和叶面积仪测量法的79.28%,更接近1。由此可得,分类拟合测算叶面积是厚竹叶面积测量的最优方法。
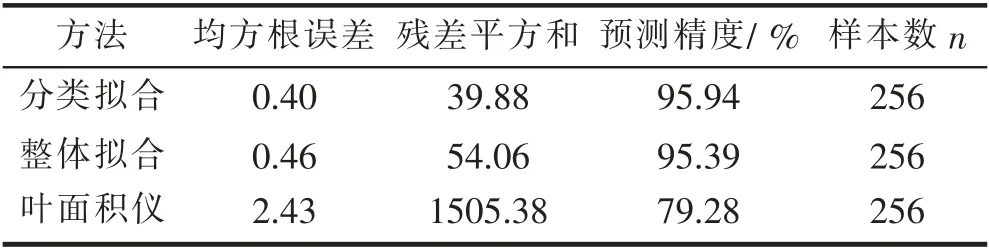
表2 不同测量方式的误差统计量Tab. 2 Error statistics of different measurement methods
从厚竹叶面积3 种测量方法所测得面积与实际面积的残差对比图可知(图2),3 种测法的残差值都分布均匀,分别集中于-2~2、-2~2 和-5~5 之间。分类拟合、整体拟合、叶面积仪所测叶面积的误差最高分别接近1、2、10,进一步表明分类拟合的精确度高于整体拟合和叶面积仪的精确度。
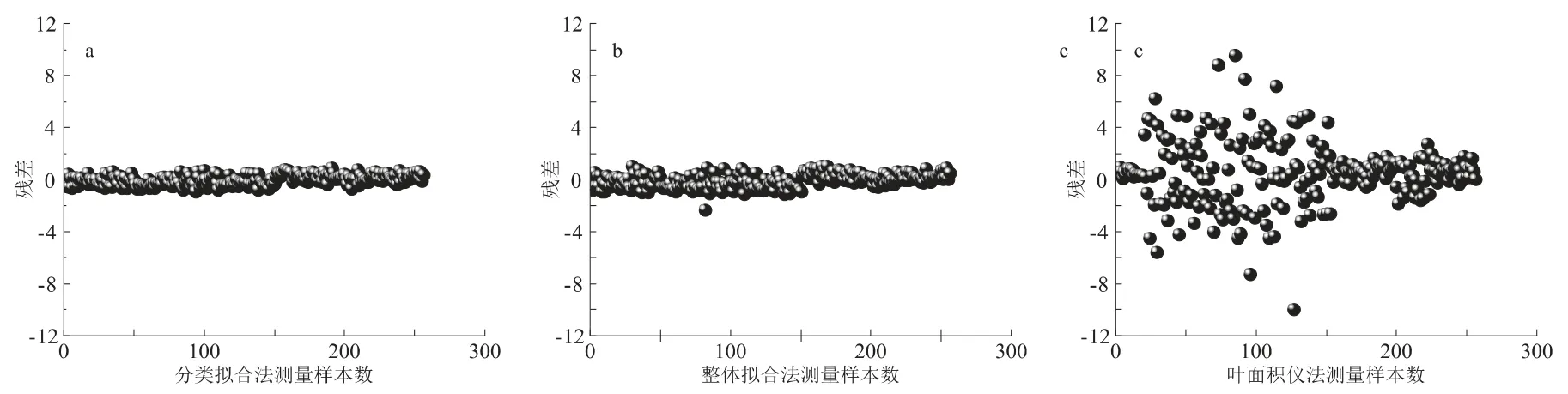
图2 测量面积与实际面积的残差Fig. 2 Residual difference between measured area and actual area
2.4 模型检验
利用预留20%样本(64 片)的长宽、面积等数据代入前述所得的分类拟合模型,并与相对应的实际面积进行比较,以检测其普适性,得出RMSE 值以及SSE 值分别为0.32、6.48,预测精度达到98.31%,大于95%,可见该模型预测精度较高。图3 为其分类拟合预测值与实际值的拟合结果,R2值为0.98,图4 为检测样本的残差分布图,可见各点随机分布,均位于-0.5~1 之间,模拟效果佳。综上,本文所得厚竹叶面积预测模型适宜投入生产应用当中。
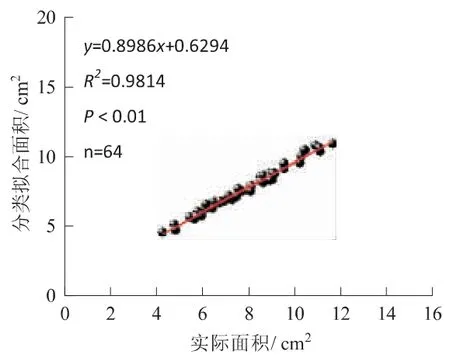
图3 分类拟合模型检验拟合度Fig. 3 Fitting degree of classification fitting model
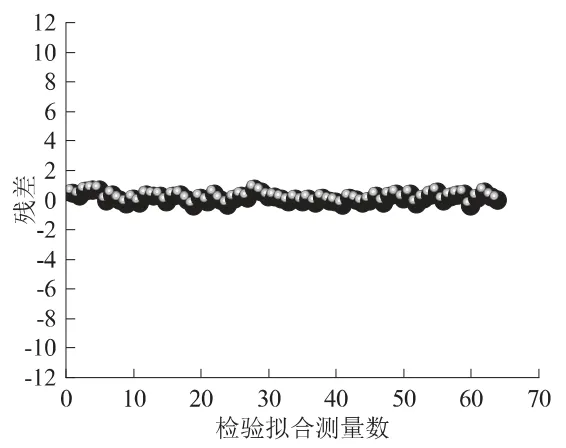
图4 检验样本拟合面积与实际面积的残差Fig. 4 Residual difference between the fitting area of the test sample and the actual area
3 结论与讨论
基于厚竹叶的形状特征,以叶片长宽比为参照,运用聚类分析把厚竹叶片分为3 类,再运用扫描所得叶片实际面积结合叶片长宽积,做出预测厚竹叶面积的模型。结果显示,分类拟合的R2值和预测精度都最高,分别为0.96 和95.94%,相对于整体拟合(R2=0.95,预测精度为95.39%)和叶面积仪法(R2=0.89,预测精度为79.28%)的结果,精度大幅度提升。本研究所得的厚竹叶面积预测模型具有快速、准确、无损测量的优点,在野外只要简单测量厚竹叶的长宽数据,即可方便地利用分类拟合模型计算出准确的叶面积,降低了野外叶面积测量的难度,为厚竹相关方面研究与实践提供了技术支撑。
不同拟合模型拟合精度不同,V. Cristofori 等[20]发现长宽积的模型相关性最好(R2为0.98,均方误差MSE 为29);杜尚嘉等[21]在研究中同样得出:长宽积与叶面积显著相关。本研究利用长宽积对厚竹叶面积进行预测,预测精度良好(R2值为0.96,图1),与前人研究所得一致。相同叶形的植物叶片进行混合建模,可以得到良好的拟合效果。吴凤婵等[22]通过分别对西番莲属(Passiflora)宽长比相似的两个种进行混合建模得到的预测精度为(92.08±0.56)%,得出叶形相近、宽长比相近的植物可以合并建模。
单种植物也存在不同叶形,巫娟等[17]通过以宽长比为依据将毛竹进行分类进而建立分类拟合模型,拟合度为0.99,预测精度达97.73%,比叶面积仪法提高13.5%,比整体拟合提高了0.38%,大大提高预测精度,同时克服了竹叶离体易卷曲对测量造成的不利影响[18];唐力为等[23]研究发现分类拟合比整体拟合R2更大,拟合效果更好。本研究汲取前人成功经验,根据叶形将厚竹叶片分为3 类,运用长宽积结合实际面积展开建模,拟合度高(R2为0.96),拟合精度好(95.94%),误差率低,相比于不分类的整体拟合法(R2为0.95,精确度为95.39%)以及叶面积仪法(R2为0.89,精确度为79.28%)的精确度都有很大提升。本方法可在采样地直接利用刻度尺测量长宽代入模型进行计算,解决了竹叶面积测量时叶片离体脱水易卷曲、仪器不易携带等问题,减少人力物力消耗,比现今广泛运用的叶面积检测仪法精度高、成本低,且比扫描测算实际叶面积简单易行,做到厚竹叶面积快速、准确、无损测量。
