考虑风电不确定性的电-气综合能源系统协调优化
2022-12-01高红均张江林刘俊勇
马 迪,高红均,张江林,刘俊勇
(1.四川大学电气工程学院,四川成都 610065;2.成都信息工程大学控制工程学院,四川成都 610225)
0 引言
近年来,我国风力发电发展迅速,截至2022 年2月全国风电装机容量约3.3×108kW[1]。风电的不确定性给多能源协调优化系统带来巨大挑战,而天然气相比于其他化石能源,具有清洁、高效等优点。
国内外学者针对电气耦合所带来的问题,提出以电转气装置(Power to Gas,P2G)等耦合元件为辅,建立综合能源协调优化系统,构建能源多向流动的电气耦合模型,将系统富余的清洁能源转化为天然气和氢气[2-3]。针对综合能源系统中的不确定性问题,部分电-气综合能源系统通过构建随机优化模型[4]、模糊优化模型[5]、静态鲁棒优化模型[6]处理。但是3 种处理方法均存在一定的局限性,随机优化方法难以对概率分布进行描述,气计算量偏大,同时在实际中其随机数也较难获取。模糊优化过程缺乏系统性,且模糊参数定值困难,目标参数求解困难。静态鲁棒优化常常难以选取最优鲁棒集合,导致决策结果偏保守。因此本文结合文献[4-6]的优化方法,改进其优化方法,通过数值天气预报(Numerical Weather Prediction,NWP)预测方法对风速情况进行预测,建立不确定信息的历史预测信息和历史实测信息,构建风场景不确定信息合集。
为充分考虑风电不确定,同时避免随机优化、模糊优化或鲁棒优化在处理风电不确定性时的不充分性,部分研究采用分布式鲁棒优化方法。文献[7-9]以分布式鲁棒模型构建风电调度两阶段优化模型,以1-范数和∞-范数作为约束条件单独或组合优化,运用列与约束生成等算法对模型进行求解,但求解难度较大,优化结果较为极端,实用性不佳。文献[10-11]引入数据驱动的随机变量建模方法,基于鲁棒优化调度实现数据驱动的不确定性集合建模,求解难度虽然较小,但计算结果偏保守,经济性较差。文献[12]以功率平衡约束、可控微源运行约束、旋转备用约束等为必要约束条件建立主动配电网优化配置模型。使用拉格朗日求导法和线性对称法将不确定性因素转化为确定性,但其分布求解方法收敛性能不佳[13]。无论鲁棒优化或是分布鲁棒优化,其优点在于能避免小概率事件发生后所带来的巨大风险,能够找出含有敏感参数的调度模型的最优解。其缺点是难以找出控制其优化性能恶劣的途径和方法,易将原确定性的参数不确定化,且求解相对繁琐,计算结果偏于片面,经济性较差。因此本文结合分布式鲁棒优化优点,分阶段对综合能源系统进行优化,以机组出力和多能耦合作为约束条件,作为模型的首阶段优化,通过Python 软件对不确定性信息进行拟合,以区间估计对不确定性合集削减,建立风速与风功率函数关系,作为模型的末阶段优化,使用改进型蝙蝠算法对模型进行求解。
对分布式鲁棒优化模型的研究,通过引入二阶锥松弛[14]对模型的非线性部分进行优化,使用交替方向乘子法调整有功潮流优化[15]。文献[16]通过储能模型的构建和调整策略,以模型的双层优化实现风电调频和风储系统运行稳定性。文献[17]以选址方法的改进,通过最优潮流和最佳线路选择配置储能系统,最大化消纳风电。风储研究抽水蓄能电站能使综合能源系统的运行收益最大化[18],同时使风电并网运行最小,但是抽蓄电站建设成本过大,经济性较差。通过储能侧构建不确定模型应对风电波动,模型简单易构,求解难度较低,但成本过高、决策灵活性不足,无法有效应对恶劣概率分布下的风功率预测。储气装置具有运用灵活,决策简单的特点,因此本文结合储气装置的出力调整最优潮流,以此保持电气能流平衡。
计及风电不确定性,本文结合风电机组、常规机组、P2G 装置等,构建电气协调优化调度综合能源系统模型,模型目标为综合能源系统运行成本最小。此外,为充分考虑风电不确定性,本文结合NWP 预测方法,以历史风速预测信息与历史风速实测信息相结合,形成预测误差累加状态转移矩阵,构建风场景马尔科夫链不确定性模型,并对模型进行削减,求得置信度最高的风场景,通过改进型蝙蝠算法对模型进行求解。最后,通过算例分析验证模型的经济性和有效性。
1 综合能源系统调度数学模型
1.1 电-气协调调度综合能源系统结构
综合能源系统以P2G 装置作为耦合单元,考虑储能元件(储气罐)的投入,当风电出力过剩时通过减小常规机组和燃气轮机机组的出力,并结合P2G装置的电气转换,将其转化为天然气供给用气负荷或是通过储气装置加以储存,从而进一步提高风电的消纳能力,其结构如图1 所示。风电不足时增加常规机组出力,同时释放风电过剩时储存的天然气,以此提高风电的利用率。

图1 电-气综合能源调度模型Fig.1 Electric-gas integrated energy dispatch model
1.2 调度模型目标函数
为了使电-气双能源系统的经济调度最佳,本文考虑系统调度的最低成本,目标函数为系统的综合成本最低,即:

式中:F1为常规机组发电成本;F2为弃风成本;F3为实际运行各机组调整成本。
1.2.1 常规机组发电成本

式中:NG为常规机组的数量;SNi为常规机组的开机成本;SFi为常规机组的停机成本;为常规机组的开机变量,为1 时为开机,为0 时表示未开机;为常规机组的停机变量,为1 时表示机组停机,为0 时为机组未停机;Pi,t为常规机组i在t时刻的有功出力;Ai,Bi,Di为常规机组i的发电成本函数系数;Ii,t为常规机组的开停机标志,为1 时表示常规机组处于开机状态,为0 时表示常规机组处于停机状态。
1.2.2 弃风成本

式中:δ为日前市场弃风惩罚系数;Nw为风电机组的数量;为第t时刻第e台风机的日前出力预测值;为第t时刻第e台风机的实际调度出力值。
1.2.3 实际运行调整费用

1.3 电网约束条件
1.3.1 功率平衡

式中:为系统t时刻的电力系统总负荷功率;NG为P2G 装置的数量,为t时刻第h台P2G 装置的有功出力。
1.3.2 常规机组、P2G装置和风力机组出力约束

式中:Pi,max为第i台常规机组的功率上限;Pi,min为第i台常规机组的功率下限;为第h台P2G装置运行的功率上限。
1.3.3 常规机组爬坡约束

式中:RDi为常规机组的滑坡速率。
1.3.4 常规机组最小开停机时间和状态约束

式中:T为调度周期的总时间段数;TOi为调度期间必须开机的时间段;TCi为调度期间必须停机的时间段;为机组最小开机时间;为机组最小停机时间;为机组i在第t时刻的连续开机时间;为机组i在第t时刻的连续停机时间。
其中常规机组的开停机变量[19]与开停机标志间应满足:
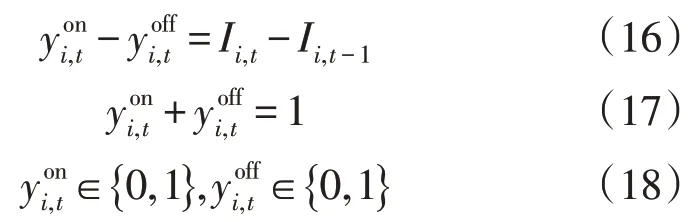
1.3.5 潮流约束
本文采用文献[20]中的直流潮流方法进行约束,具体数学模型为:

式中:a(m)为节点m为主节点的节点集合;Vm,t为t时刻节点m的电压幅值;Vd,t为t时刻节点d的幅值;gmd为支路md的电导;bmd为支路md的电纳;bsmd为支路md对地的导纳;θmd,t为t时刻节点md之间的电压相角差;qa,t为t时刻主网注入的无功功率;qL,t为t时刻负荷消耗的无功功率。
1.3.6 备用约束
电气系统中将常规机组作为备用机组,机组的约束具体形式为:

式中:rwind为风电的旋转备用率,取10%。
1.4 天然气网络约束条件
1.4.1 节点气压约束
在天然气网络中,每个节点都有压力上下限值为:
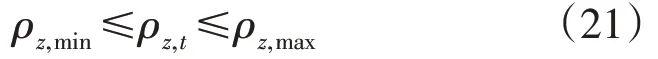
式中:ρz,t为第z个节点t时刻的气压;ρz,min为压力下限;ρz,max为压力上限。
1.4.2 质量守恒约束
天然气网中的天然气流向要符合质量守恒定则,即任意节点的天然气流入量等于流出量,即:

1.4.3 天然气系统潮流约束
对任意管道的管道流量与节点压力需满足以下关系,即:

式中:ρz为节点z的气压;ρw为节点w的气压;Czw为由管道摩擦力、温度、平均压缩因子等决定的综合参数。
sgn(ρz,ρw)为管道的流动方向,定义为:

1.4.4 气源注入量约束
对于天然气气源的供气量需满足的约束条件为:


1.5 电-气耦合元件约束条件
P2G 装置的电-气耦合约束为:

式中:ηP2G为P2G 装置的转换效率,本文取80%。
2 风电不确定性模型的建立与削减
2.1 风电不确定性模型的建立
风电功率的预测是风电并网消纳的重要条件,如果无法较为准确的预测风功率,则大型风电场的建设和并网都将受到限制。为充分考虑到风电的不确定性特性,本文以某地区风速实测数据和历史风速预测数据为基础,构建风场景不确定性信息。马尔科夫链模型[20]对于生成风光等不确定性因素具有较为宽泛的运用,而NWP 方法能对风速进行预测[21],本文选取模型区域合集历史NWP 数据作为不确定性信息合集,选取各样本历史风速观测数据,通过与历史风速预测数据相比较,并根据风速预测误差的变化范围将其划分为n个区间,并将风速预测误差值转化为n个对应的离散量s1,s2...sn,设t时刻风速预测误差离散量为si,则第t+1 时刻的风速预测误差离散量为sj的概率为p()vt+1=sj|vt=st,设不确定性信息合集共有n个预测误差,将误差合集设为状态转移矩阵P[20],其中:

由式(29)可求得累加状态转移矩阵Q,详见文献[20]。通过未来预测信息和预测误差状态转移矩阵可以构建多组风场景,任意1 组风场景作为1 个不确定性模型的基础样本,其中每个基础样本为服从形状参数k和尺度参数λ的威布尔分布函数[22],从而形成若干个服从威布尔分布的风场景基础样本,通过Python 建模,使用最小二乘法拟合曲线可以求得任一基础样本的形状参数和尺度参数[23]。最后对总样本进行削减,而将削减后的风功率场景作为双能源系统中的风功率预测场景模型。
2.2 不确定条件下风场景的削减
本文取不确定性模型基础样本n个,分别对应n组风场景,其中,第j个风场景的风速vj是服从形状参数kj和尺度参数λj的威布尔分布函数,第j个风场景的风速概率密度函数和分布函数分别为:
式中:fV(v)为风速概率分布函数;j=1、2、3......n;f(v,k,λ) 为风速概率密度函数,任一风电场景的概率为;和分别为n组风电场景的风速概率密度函数的形状参数和尺度参数的期望。
本文再补充一点说明:概念既然是语言系统任意地切分出来的,不同的语言系统切分出来的概念就没有完全对等的可能性;但对于“牛”这类有实体指称的词而言,不同的系统切分出来的概念刚好就是相同的[15]。陈嘉映指出了其中的原因,“语言系统对概念的区分不是完全任意的。例如自然品类,杨树、柳树、松树等等,它们的分界线差不多是由现实强加给语言的”[9]77。总之,任意性不是绝对的,而是相对的[9]77,索绪尔最终未能将事物从符号中排除出去。
将风速概率密度函数f()v,k,l的形状参数k和尺度参数λ作为特征值进行参数估计,估算形状参数k时,设尺度参数λ为已知,用替代。估算尺度参数λ时,设形状参数k为已知,用替代。从而将风功率密度函数转换为服从λ或者服从k的单参数分布。取枢轴量函数为:
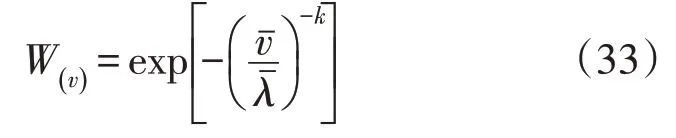
式中:为n风场景的风速期望。
W的分布不依赖于k和λ。估算尺度参数λ时,由式(33)取不等式(34)与式(36)即:

式中:a,b为2 个常数;1-α为置信水平;α为显著性水平。
式(34)和式(35)为2 个等价的不等式。对λ进行估计,由此得到所估计λ的置信水平为1-α的2组区间。由式(33)—式(36)可得:

由式(37)即得到λ的置信水平为1-α的置信区间为:
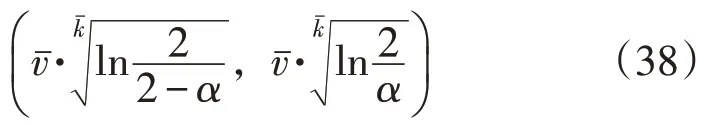
同理估算形状参数k时,可得k的置信水平为1-α的置信区间为:

式(38)和式(39)的交集部分即为削减后的s个典型风电场景。式(30)中,第j个风电场景的风速期望为:
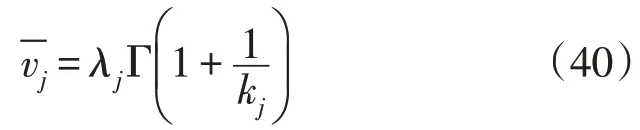
其中,式(40)相关函数值可由式(41)求得:

n个风电场景中,其形状参数和尺度参数同时在二者置信区间内的风场景即为削减后的风场景。
2.3 不确定性条件下的风电功率的随机性模型
本文随机优化模型以常规机组运行成本、弃风成本、实际各机组运行调整成本最小作为系统优化目标,以电网及天然气网络各机组运行约束、功率平衡约束、潮流约束、电气耦合约束作为系统约束条件。通过风速预测误差状态转移矩阵构建服从威布尔分布的风场景基础模型,并以区间估计对模型进行削减,获取最优场景。将风速与风电功率的关系简化,且文中的每台风力机是同一型号同一标准的,任一风机的切入风速、切除风速以及额定风速完全一致,具体处理方法参考文献[24]。
2.4 模型求解
本文使用改进型蝙蝠算法(Improved Bat Algorithm,IBA)对综合能源调度模型进行求解,传统的蝙蝠算法(Bat Algorithm,BA)基本结构及流程见文献[25]。由于传统蝙蝠算法具有收敛易早熟,易出现极值,形成局部最优解等缺点[26],本文引入随机扰动对传统的蝙蝠算法进行改进[27]。加入速度权重系数,以此继承前一代的学习速度,当运动后的位置使得目标函数值优于前一代位置,则说明这一代的位置离最优目标函数值更近一步,再通过加大或者削减速度的学习权重,以此使得蝙蝠具有趋近避远的习性,提高算法性能,其表达式为:
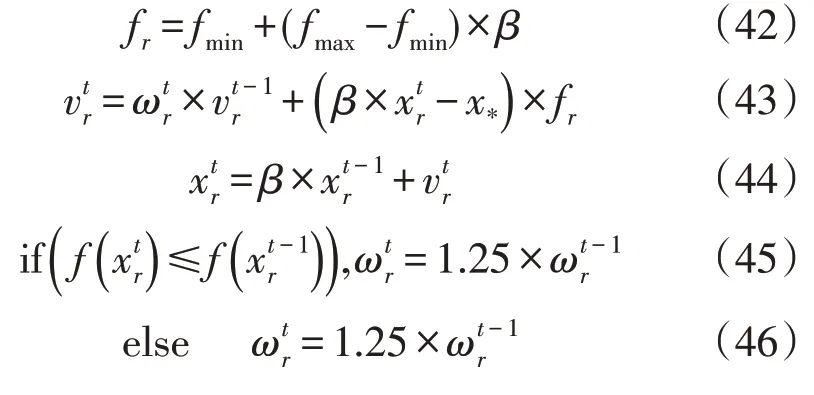

式中:fr为第r只蝙蝠发出的频率;fmax,fmin分别为最大频率和最小频率;为第r只蝙蝠第t时刻的速度;为第r只蝙蝠第t-1 时刻的速度;x*为当前种群最优解;为第r只蝙蝠第t时刻的位置;为第r只蝙蝠第t-1 时刻的位置;β∈(0,1)为1 随机数;ε∈[0,1],为1 个随机数;xnew为更新位置;xold为旧位置;α∈(0,1),为声波响度衰减系数;At为t时刻种群平均响度;为蝙蝠初始脉冲速度;为t+1 时刻蝙蝠脉冲频度;γ>0,为脉冲增强系数。
电气综合能源系统模型求解流程如下:
1)输入综合能源系统参数和IBA 算法参数。系统参数包括用户负荷、机组出力上下限、约束条件等,IBA 算法参数包括蝙蝠种群规模、响度、频率等。
2)基于各机组出力上下限,映射初始化蝙蝠位置[26]。
3)寻出当前最优蝙蝠位置后,根据式(42),式(43)和式(44)更新蝙蝠频率、速度和位置。
4)生成0和1之间的随机数rand1,若rand1 >cr,则式(47)处产生1 个局部最优解。
5)生成随机数rand2,若rand2 <Ar,且f(x*),则接受该位置,并由式(48),式(49)更新响度和脉冲频度。
6)寻找出最优蝙蝠位置。
7)重复步骤3)—6)直至最大迭代次数,输出综合能源系统成本最优方案。
3 算例分析
3.1 算例构成
本文算例选用修改后的IEEE-39 节点系统并参考文献[7]的6 节点天然气系统。综合能源系统使用Matlab-R2016a 进行仿真验证。风电场的相关风速参数参考文献[14],蝙蝠算法相关参数参考文献[26]。
3.2 电气综合能源系统优化调度结果
本节在计及风电不确定性条件下,通过对综合能源系统优化调度,来对比不同模型不同算法下综合能源系统及其算法的有效性。
3.2.1 不同置信水平下的风功率预测情况
风功率预测模型共得到1 000 个预测场景,即1 000 组基础样本。对基础样本进行削减,当置信水平取值不同时,所削减后的风场景个数也不同,随着可信度的增加,削减的风场景个数越多,得到的风场景越少。不同置信水平所削减后的各个风场景风电预测功率如图2 所示。
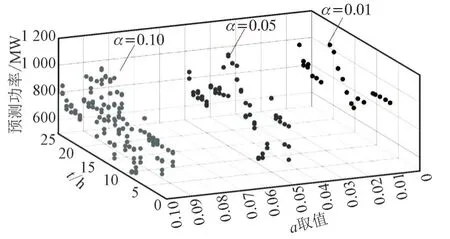
图2 不同置信度下风功率预测情况Fig.2 Prediction of wind power with diffierent confidence levels
当显著性水平α分别取0.01,0.05,0.1 时,削减分别得到1 组,3 组,7 组风场景。7 组风场景分别对应7 个风速v为服从尺度参数k和形状参数λ的威布尔分布函数。
3.2.2 综合能源系统风电消纳情况及综合成本
当显著性水平取0.01 时,可信度达到最高,只削减得到1 组风场景,该风场景也最接近未来风功率预测情况,因此,本文将该场景作为典型风场景,并将其带入综合能源系统求解,从而求得各机组出力如图3 所示,其中功率为负表示发电,为正表示用电。

图3 综合能源系统各机组出力情况Fig.3 Each unit output in integrated energy system
凌晨时期为负荷低谷期加装电转气装置能显著改善弃风状况,提高风电的利用率。电转气装置配合储气装置,负荷低谷时期将多余的电能转化为天然气加以储存或是直接利用,在负荷高峰时期再进行释放,从而形成能流动态平衡。
3.2.3 模型优化结果对比
为验证本文所提出模型和相关算法的实用性和正确性,本文将所提出模型与传统随机优化模型与模糊优化模型进行对比,以获取的1 000 个预测场景进行调整成本的期望值和最大值对比分析。其中本文模型分别选取3 个不同置信水平下削减后所得风场景进行验证,计算结果如表1 所示,其中本文所提模型显著水平性α取0.1 时,优化结果如第1 行所示;α取0.05 时,优化结果如第2 行所示;α取0.01时,优化结果如第3行所示。其余2种优化模型不涉及本文所提出的模型削减方法,优化结果与α无关。
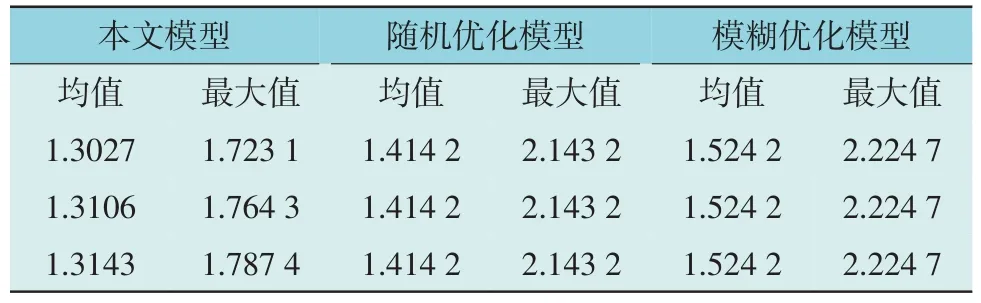
表1 不同模型总成本优化结果对比Table 1 Comparison of different model optimization results (×106$)
由表1 可知,相比于随机优化模型和模糊优化模型,本文提出模型经济性能更佳,成本更低,随着精确度的增高,风电预测信息越准确,成本有所上升。本文模型中的平均值和最大值均优于其它2种模型,说明本文所提模型波动性更弱,对不确定性的稳定更强。
针对本文所提出模型,分别使用BA 与标准粒子群算法(Particle Swarm Optimization,PSO)求解,并与本文算法进行比较分析,其结果如图4 所示。
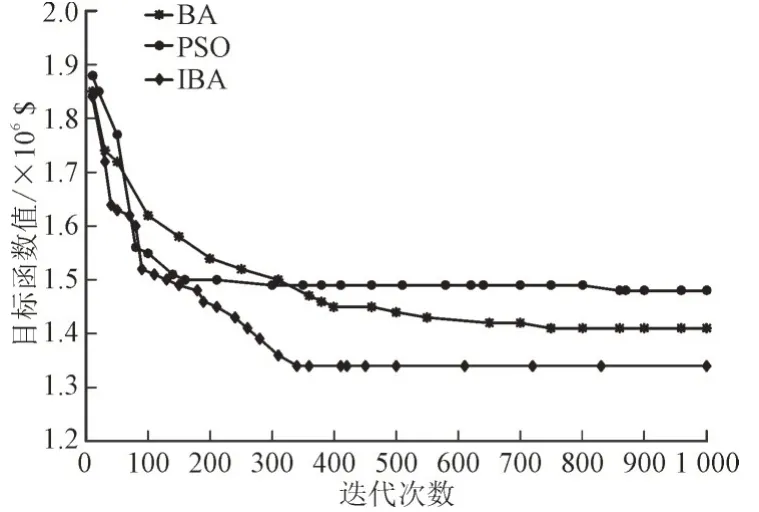
图4 不同算法对模型求解的寻优路线Fig.4 Optimal routes for model solved by diffierent algorithms
由图4 可知,由于传统的蝙蝠算法与标准粒子群算法具有易陷入局部最优的特点,致使算法结果不理想,且迭代次数也相对较多,收敛较慢,而改进型蝙蝠算法由于加速权重系数的加入,收敛更快,收敛精度更高,算法性能更优。
4 结论
本文以传统能源、电转气(P2G)装置和储能元件的耦合,构建电-气综合能源系统,目标函数为综合能源运行成本最优,所得如下结论:
1)综合能源系统能有效地增大风电的消纳,减少弃风,历史风功率预测情况跟置信区间有关,随着精度的增加,削减后的风功率数据越少。
2)本文通过构建风电不确定性合集,再对其基础场景样本进行削减,在充分表征样本的不确定的同时,又筛选出最具代表性的样本,提高预测精度。最后通过系统各机组的出力调整以应对风电的不确定性。
3)蝙蝠算法能有效对综合能源系统进行求解,但是其易在极值收敛的特性也会影响模型最终成本,因此加入权重系数能有效提高算法收敛精度,减少模型调度成本。
