基于改进的基本效应法的网壳结构构件重要性分析方法
2022-12-01栗云松罗永峰郭小农张玉建
栗云松,罗永峰,郭小农,张玉建
(1.同济大学土木工程学院,上海 200092;2.广州市住房和城乡建设局,广东 广州 510032;3.中国建筑第八工程局有限公司,上海 200120)
钢结构检测与鉴定多从构件层面出发,通过对构件的安全性评定,进而评定整个结构的安全性。由于实际结构构件数量往往很多,对所有构件进行检测成本很高,因此一般采用抽样方法进行检测。抽样检测方法通常将构件划分为重要构件和一般构件,并对两类构件分别制定不同的检测鉴定方案[1]。然而,现行检测鉴定规范[1-4]均未给出一般构件和重要构件的定量判定方法。同时,与框架结构相比,对空间网壳结构构件重要性的研究也相对较少。
重要构件通常指其失效或损伤后会造成结构严重损伤或破坏甚至可能倒塌的构件[3]。为确定结构中的重要构件或计算构件的相对重要性,基于能量的重要性判定方法[5-7]根据构件损伤或拆除前后结构应变能的变化判定构件的重要性,基于刚度的重要性判定方法[8-9]根据构件拆除前后结构整体刚度的变化判定构件的重要性,基于应力比的重要性判定方法[10]根据构件拆除前后构件平均应力比的变化判定构件的重要性。综合现有构件重要性方法的计算思路,可以将此类方法称为形式不同的局部灵敏度分析方法,即考察单个构件损伤或失效对结构整体性能影响的方法。此类局部灵敏度分析方法概念清晰、操作简便,得到了广泛的应用,但将其应用于网壳结构中时仍存在局限性:①网壳结构具有强非线性,局部分析可能无法提供有效的分析结果;②局部灵敏度分析方法只研究单根构件的损伤或失效,忽略了实际工程中其他构件存在的不同程度的损伤(或失效)对分析结果的影响。
相较于局部灵敏度分析方法,全局灵敏度分析方法可以考察所有不确定参数(构件损伤)共同变化对结构整体性能的影响,具有更强的适用性。现有的全局灵敏度分析方法中,基本效应法应用广泛,该法通过基本效应遍历输入变量空间,进而分析输入变量在其分布区域变化时对模型输出响应的平均影响。针对构件数量众多且非线性效应较强的网壳结构,基本效应法相对于其他方法计算代价较低,计算效率较高,因此本文将基本效应法应用于网壳结构的构件重要性计算。然而,经典的基本效应法仍存在诸多限制,不能直接应用于结构检测前的构件重要性分析。这些限制主要有:①基本效应是根据输入变量发生微小变化时的输出变量变化率定义的,而网壳结构在单根构件发生微小变化时整体承载能力基本不变,从而经典定义下的基本效应结果对所有构件的结果都为0,缺乏应用价值;②基本效应法对所有输入变量都采用多次模拟的方式计算其基本效应,但网壳结构的重要构件数量通常较少,对所有构件进行相同的大规模非线性有限元模拟计算较为浪费;③基本效应法仅给出了重要变量与不重要变量的判定方法,未给出重要变量内部的相对重要性排序判定方法,但实际检测中限于成本可能无法检测全部重要构件,仅能检测重要构件中最为重要的部分构件,因此有必要研究网壳结构构件的重要性排序方法。
为解决现有的构件重要性分析方法的不足,本文将基本效应法应用于网壳结构构件的重要性判定;同时,为解决基本效应法不能直接用于构件重要性计算这一问题,针对网壳结构类型重新定义基本效应,并提出用于确定重要构件的双阶段判定方法和重要构件的构件重要性排序方法,进而提出基于改进的基本效应法的网壳结构构件重要性分析方法。此外,为减小改进的基本效应法的计算量,提出适用于本文方法的修正径向抽样方法。最后,基于两个凯威特网壳结构数值算例计算结果,通过与现有的基于损伤的构件重要性方法和基于拆除的构件重要性方法对比验证本文方法的有效性。
1 改进的基本效应法
1.1 基本效应
与竣工时的结构相比,由于服役期内各种不利因素的影响,结构构件会出现裂纹、腐蚀、变形等损伤甚至累积损伤,导致结构承载能力降低。一般认为,构件的损伤可以等价表示为结构局部刚度的损失,基于此,在构件重要性分析时,本文将结构局部刚度的损失表示为单根构件横截面面积的降低,并将构件截面面积的降低比例表述为构件削弱程度。同时,构件i的削弱程度记为Xi,所有构件的最大削弱程度记为Xmax。
参考Morris[11]对基本效应(elementary effect,EE)的定义,可以将构件i的基本效应表示为REE,i,且其定义为:在所有构件都带有某种程度的损伤时,当构件i的削弱程度Xi增加Δi时所引起的网壳整体性能指标g的变化量与Δi之比,即:

式中:N为构件总数;Δi为构件i的削弱程度Xi的变化步长;(X1,X2,…,XN)为所有构件的削弱程度,记为样本点X,并需满足Xi+Δi<Xmax(i=1,…,N);g(X1,X2,…,XN)为对应于含有所有构件削弱程度的样本点X的经有限元软件模拟计算或其他理论方法分析确定的网壳结构整体性能指标。
若将构件削弱程度分布区间[0,Xmax]均分为p级 , 则Δi可以取
单层网壳结构的整体失稳通常是局部构件失稳引发的失稳传播所致[12]。当构件i不属于首先失稳的局部失稳区域内的构件时,若构件i的削弱程度由Xi变化为Xi+Δi,则整体失稳的发展过程不受影响,从而网壳结构稳定承载力并不因构件i的削弱程度变化而变化。对这一情况,根据公式(1)计算得到的g(X1,X2,…,XN)=g(X1,X2,…,Xi+Δi,…,XN),故REE,i=0,从而,直接将经典的基本效应定义应用于网壳结构构件重要性计算时,会导致基本效应(EE)的主要部分都为0,从而不同构件的基本效应之间缺乏辨识度,无法实现从大量的构件中筛选出重要构件的分析目标。
针对经典基本效应不适用于构件重要性计算的问题,本文提出将构件i的基本效应REE,i定义修正为:在所有构件都带有某种程度损伤时,构件i的削弱程度Xi变为Xmax引起的网壳整体性能指标g的降低率;即将式(1)修改为
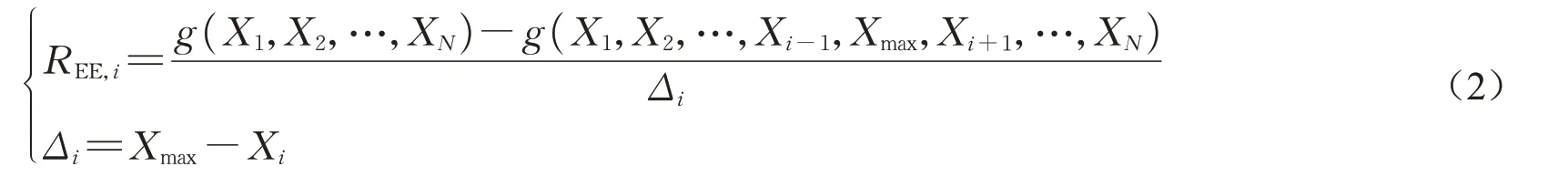
与现有的重要性判定方法非常类似,式(2)将单根构件的损伤提高到一个较大程度,以使网壳整体指标有发生明显变化的可能;同时,式(2)在分析单个构件的损伤对网壳整体性能的影响时,考虑了其他构件有损伤的情况,继承了基本效应法的优点。此外,本方法和现有重要性判定方法都未考虑实际结构构件损伤之间可能存在的相关性,而假定各构件损伤之间相互独立。
1.2 重要构件的双阶段判定方法
式(2)所定义的基本效应REE,i仅是一个局部的灵敏度测度。为了得到一个全局的灵敏性的测度,Morris[11]考虑REE,i的分布Fi,提出了用Fi对应的均值μi和标准差σi作为输入变量Xi的灵敏度测度,即:
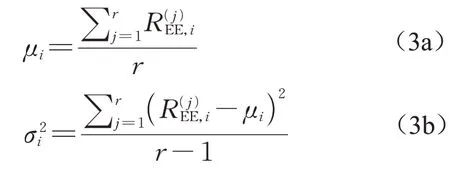
式中:r表示基本效应的个数,并称为区块数;i表示构件编号;j表示区块数编号。
由式(3)可知,均值μi表示输入变量Xi在其整个分布区间内变化时对输出响应g的平均影响;标准差σi表示Xi与其他变量变化之间的相互影响对输出的影响是线性的还是非线性的。
已有研究[7]表明,网壳结构中存在着大量的一般构件,即基本效应REE,i的μ基本为0的构件。考虑到有限元模型计算较为耗时,且基本效应法中判定单根构件的重要性需要计算r个基本效应,因此为提高确定重要构件的效率,需要减小不重要构件的计算耗时。
为实现这一目的,本文提出在正式计算之前,进行一次试算,即首先设定一较小的区块数rs,以计算得到每根构件的基本效应的μ和σ。考虑到重要构件的损伤会对结构性能产生较为明显的影响,因此,即使试算的区块数rs较小、μ和σ的估计值存在较大误差,重要构件基本效应的μ和σ也应当显著地大于0。从而,可将试算中基本效应基本为0的构件直接判定为一般构件;对于基本效应较大的构件,直接将其判定为重要构件则误判概率较高,应进一步分析。考虑到有限元模型计算误差[13]可能达到0.02,因此在试算环节中,本文判定μ+σ≤0.02的构件为一般构件,并将μ+σ>0.02的构件称为待观察构件,以待后续正式计算确定其中的重要构件。本文定义待观察构件的判定式为

本文将满足式(4)的所有构件称为待观察构件组,对应的编号记为Mob={m1,m2,…,mn},其中n为待观察构件个数。
为确定待观察构件Mob中的重要构件,应在正式计算中采用一较大的区块数r,根据式(3)计算相应的基本效应。计算得到待观察构件的灵敏度测度μ和σ后,本文综合考虑有限元数值计算可能的误差,给出了同时考虑均值μi和标准差σi时的重要构件判定标准:
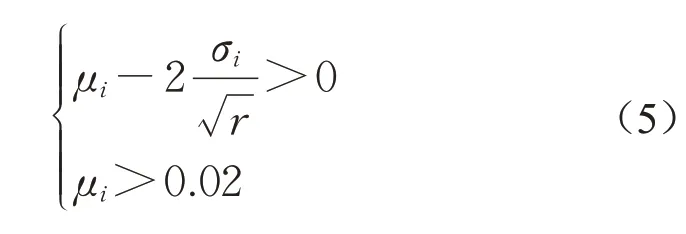
由式(5)的定义可知,重要构件的削弱程度Xi在全局范围内变化时,其基本效应REE,i都大于0,即构件i的削弱程度由一随机值增加至Xmax时,网壳整体稳定承载力将会发生显著降低,结构发生严重损伤。此外,与不满足式(4)的构件类似,不满足式(5)的构件即为一般构件。
1.3 构件重要性排序方法
为确定重要构件内部的构件重要性排序,本文基于优劣解距离法(technique for order preference by similarity to an ideal solution,TOPSIS)同时考虑输入变量Xi的灵敏度测度:即均值μi和标准差σi。基于该两个参数进行构件重要性的判定问题属于多属性决策问题,解决此类问题,TOPSIS法[14]是目前最广泛使用的方法之一。TOPSIS法首先构造多属性决策问题的理想解和负理想解,然后以评价对象与理想解和负理想解的距离作为参数,判断各评价对象的相对优劣。
采用TOPSIS法判断结构中各重要构件的相对重要程度时,可以将参数μi和σi组成有序数对(μi,σi),进而将该有序数对作为评价对象,并构造关于(μi,σi)的理想解和负理想解。理想解实际上就是构件损伤影响均值最大且变异性最小的情况,即μi=μmax且σi=0;负理想解就是构件损伤影响均值最小且变异性最小的情况,即μi=0且σi=0。因此,TOPSIS法就是根据各重要构件的(μi,σi)与理想解(μmax,0)和负理想解(0,0)的距离大小关系评价重要构件的相对重要性。
重要构件的(μi,σ)i与理想解的距离Di+和与负理想解的距离Di—,可采用下式计算:
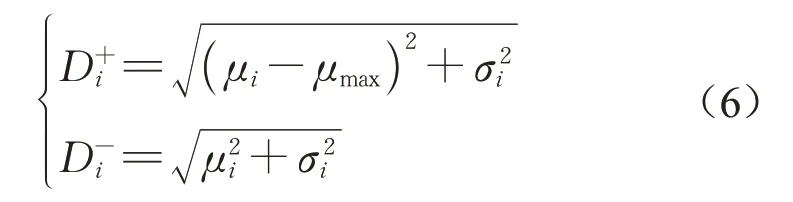
根据式(6)计算得到Di+和Di—后,可计算相对接近度Ii,如下:
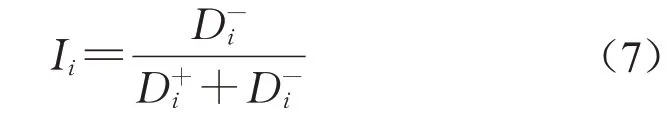
由式(7)可知,Ii越大,重要构件的(μi,σi)与理想解的距离越近,与负理想解的距离越远,表明该构件越重要。因此,可将相对接近度Ii定义为构件重要性系数,用于计算结构中重要构件的相对重要性。
1.4 修正径向抽样方法
计算输入变量Xi的灵敏度测度均值μi和标准差σi的关键是产生r个基本效应REE,i的样本。由式(2)可看出,计算一个REE,i需要两个样本点,因此,对含有N个构件的网壳共需要2rN个样本点来计算式(2)中的指标。实际计算中则常利用轨道抽样方法[11]、改进的轨道抽样法[15]、径向抽样方法[16]和改进的径向抽样方法[17]等抽样方法以将计算所需的样本点个数由2rN个降低至r(N+1)个。在上述方法中,径向抽样方法根据一个相同的基准点a1和不同的辅助点(a2,a3,a4)来计算不同构件的基本效应,可以在相同的轨道数下实现比轨道抽样法更高的精度[17]。图1为在三维空间内针对某仅含3根构件的结构给出径向抽样方法所生成的一个区块的示意图。在该区块内共有1个基准点和3个辅助点,通过基准点和其他任意一个辅助点可以针对某一个构件计算出一个基本效应。从而一个区块可以针对每一根构件分别计算得到出一个基本效应,r个区块可以针对每一个构件分别计算出r个基本效应,从而可估计出全部构件的灵敏度指标。
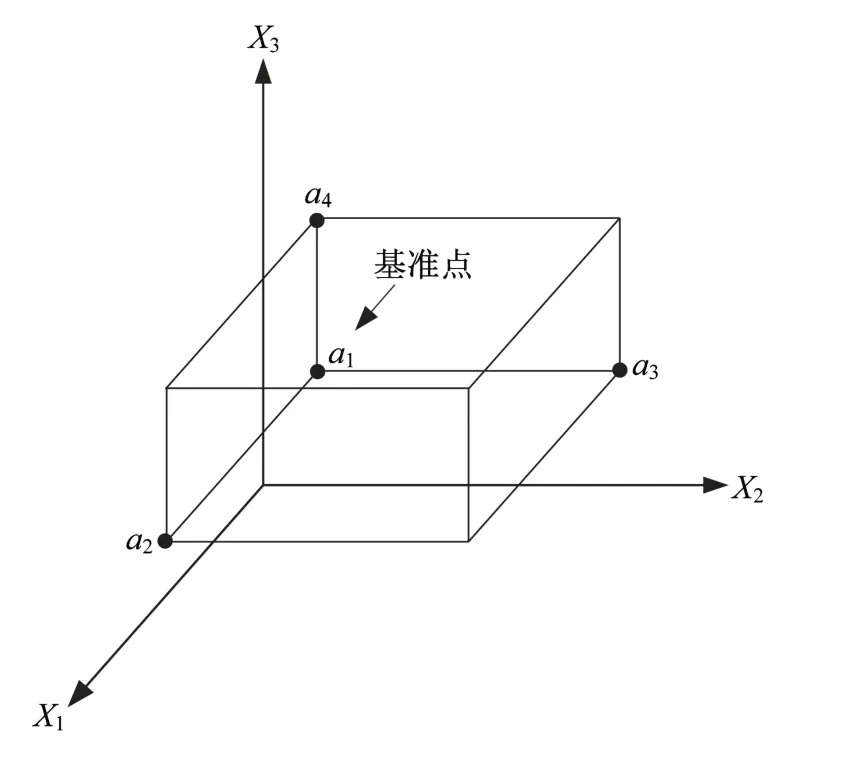
图1 三维空间内一个区块的示意图Fig.1 An example of a block in 3D space
考虑到本文提出的改进的基本效应法在计算不同的基本效应时步长Δi不同,因此,本文在Campolongo等[16]研究成果的基础上,提出了适用于本文方法的修正径向抽样方法。其中,为计算结果具有代表性,本文根据文献[17]建议采用Sobol序列选取基准点以保证所得到的r个区块具有较高的分散度,从而保证计算结果的准确。此外,试算过程和正式计算过程中分析构件数量不同,相应的修正径向抽样法的步骤也有所不同,两阶段对应的修正径向抽样法的具体步骤如下。
第一,试算阶段,需针对所有构件在输入变量空间内建立rs个区块,每个区块包含N+1个样本点,共需要rs(N+1)个样本点,基本过程如下:
(1)生成一个N维Sobol低差异序列;
(2)根据Sobol序列第i行中数据,产生一个基准点ai=(a1,a2,…,aN),其中a1,a2,…,aN代表所有构件的削弱程度。
(3)将基准点ai作为区块的第一个样本点。
(4)通过将基准点ai的第j个坐标替换为Xmax得到第(j+1)个样本点。
(5)令步骤(4)中的j分别取1,2,……,N,从而得到区块中其他的样本点,并得到一个含有N+1个样本点的区块。
(6)重复步骤(2)~步骤(5)共rs次可以得到rs个区块,rs(N+1)个样本点。
第二,正式计算阶段,需针对待观察构件组Mob={m1,m2,…,mn}中的n根待观察构件在输入变量空间内建立r个区块,每个区块包含n+1个样本点,共需要r(n+1)个样本点,基本过程如下:
(1)生成一个N维Sobol低差异序列;
(2)根据Sobol序列第i行中数据,产生一个基准点ai=(a1,a2,…,aN)。
(3)将基准点ai作为区块的第一个样本点。
(4)通过将基准点ai的第j个坐标替换为Xmax得到第(j+1)个样本点。
(5)令步骤(4)中的j分别取m1,m2,……,mn,从而得到区块中其他的样本点,并得到一个含有n+1个样本点的区块。
(6)重复步骤(2)~步骤(5)共r次可以得到r个区块,r(n+1)个样本点。
2 基于改进的基本效应法的构件重要性计算流程
对一个具有N根杆件的网壳,采用本文提出的基于改进的基本效应法,计算网壳结构构件重要性的步骤如下,具体计算流程如图2所示。

图2 本文构建重要性分析方法流程图Fig.2 Flowchart of proposed member importance analysis method
步骤1确定或假定网壳结构构件缺陷的分布类型,根据该分布类型假定可能的最大构件缺陷程度Xmax。
步骤2基于修正的径向抽样法生成rs个区块(rs为一较小值)的样本点,根据样本点在有限元软件中建立结构模型,并对全部N根构件进行试算,计算得到每个区块中每个点所对应的带缺陷网壳的极限承载力。其中,样本点包含了所有构件的削弱程度信息。
步骤3根据式(2)计算基本效应,根据式(3)计算试算阶段中各构件全局灵敏度指标μ和σ的估计值。
步骤4基于式(4)将所有构件划分为待观察构件和一般构件,其中待观察构件记为Mob={m1,m2,…,mn},一般构件记为MU1。
步骤5基于修正的径向抽样法生成r个区块(r为一较大值)的样本点,根据样本点在有限元软件中建立结构模型,对Mob中的n根构件进行重点计算,计算得到每个区块中每个点所对应的带缺陷网壳的极限承载力。
步骤6根据式(2)计算基本效应,根据式(3)计算重点计算阶段中各待观察构件的全局灵敏度指标μ和σ的估计值。
步骤7基于式(5)将所有待观察构件划分为确定重要构件和一般构件,其中重要构件记为MI={m1*,m2*,…,mc*},一般构件记为MU2。
步骤8根据步骤4和步骤7确定一般构件为MU=MU1+MU2。
步骤9根据步骤6得到的灵敏度指标μ,确定合适的最大均值μmax;随后,对步骤7所得的重要构件MI,根据式(6)和式(7)计算构件重要性系数Ii,确定重要构件的重要性排序。
3 数值算例
3.1 算例一
3.1.1 网壳结构模型
本节以一带构件损伤的凯威特型单层网壳为例,验证本文方法的有效性。该网壳跨度70 m,矢跨比1/3,网壳结构环向划分为8个相同扇形曲面,径向分为9环,其几何模型如图3所示,共361个节点和1 008根杆件。杆件采用圆钢管,主肋杆和环杆截面尺寸为146 mm×5.5 mm,斜杆截面尺寸为133 mm×4.0 mm,钢材强度等级为Q235、弹性模量E=2.06×105MPa、泊松比为0.3、质量密度为7 850 kg·m-3。构件损伤以截面面积降低比例d表示,且在区间[0,50%]服从均匀分布。网壳结构节点均为刚性连接,支座为三向固定铰接。恒荷载取0.3 kN·m-2,活荷载取0.5 kN·m-2,满跨分布。屋面荷载按壳表面积(活载按投影面积)等效为集中荷载施加在节点处。本算例使用通用有限元软件ANSYS 17.0分析计算,其中构件选用空间弹塑性梁单元BEAM188模拟。
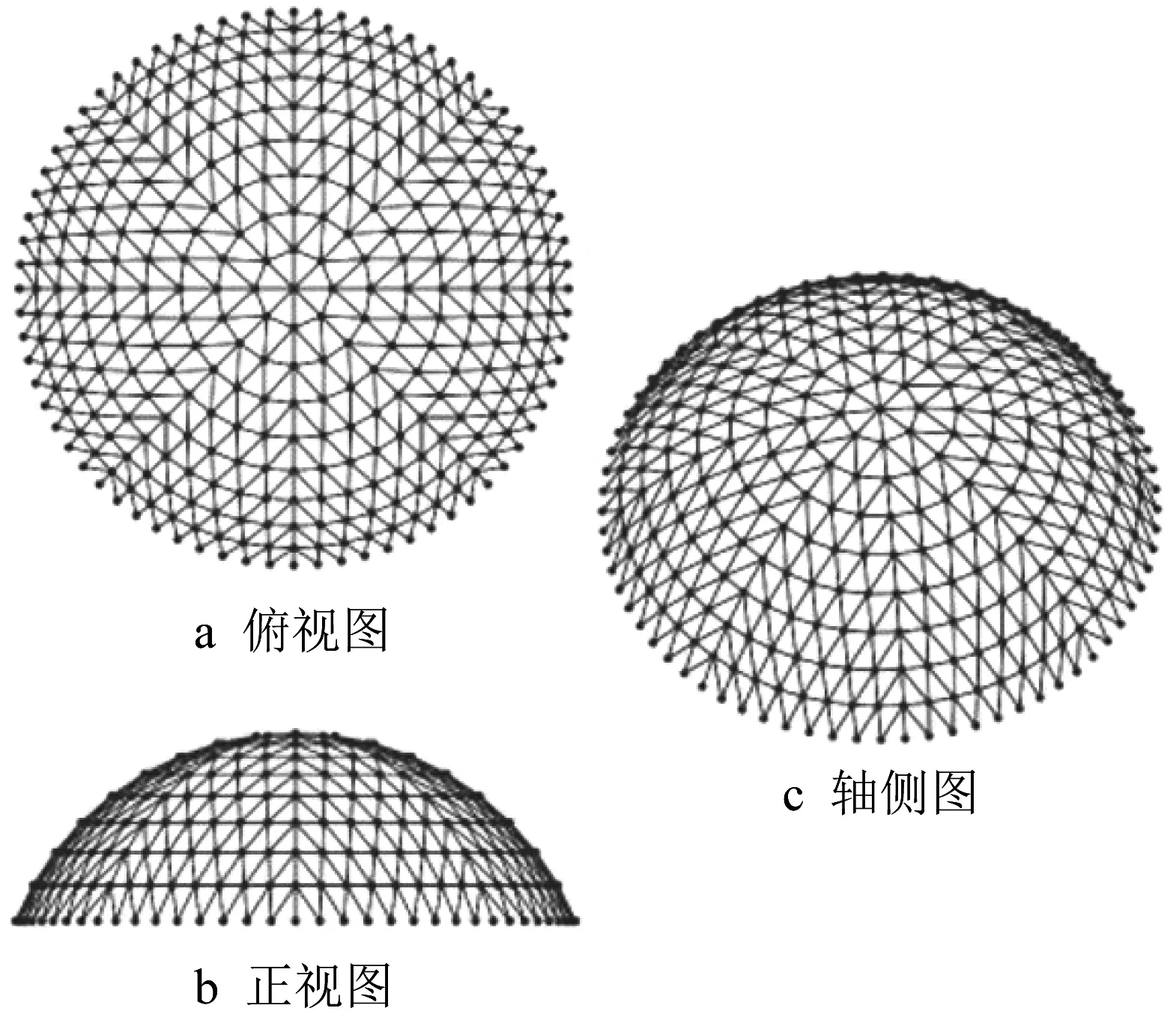
图3 70 m跨度K8网壳示意图Fig.3 Diagrams of a K8 shell of 70m span
3.1.2 构件重要性计算结果
为提高计算效率,在计算网壳构件的重要性时仅计算一个扇形曲面内所有构件的重要性结果,该扇形曲面及其内部构件编号如图4所示。试算时,较小的区块数rs取20。图5给出了不同构件的基本效应的均值μ和标准差σ的计算结果,并在图中给出了待观察构件的构件编号。由于一般构件个数较多,且结果相近,不易以图的形式表示,图5中未给出一般构件的构件编号。
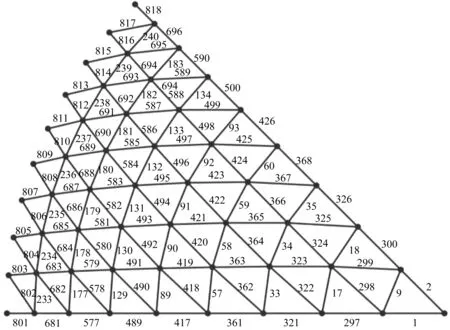
图4 扇形曲面及其构件编号Fig.4 A sector shell and its member number
由图5可知,在试算中,579、491、419、9和417号构件基本效应较为显著,满足式(4),表现为待观察构件;其他构件的基本效应均值和标准差都接近0,表现为一般构件。待观察构件中,491和9号构件的计算结果较为集中,满足重要构件的判定标准式(5);579、419和417号构件的基本效应均值较大、标准差也较大,表明其构件削弱对结构整体性能的影响与其他构件存在较为明显的耦合效应,应当在后续分析中重点观察。
为进一步确定重要构件,正式计算中区块数r取为200,并仅对491、9、579、419和417号构件进行分析,其基本效应灵敏度指标结果如图6所示。
综合图5和图6可知,试算过程中满足重要构件判定标准式(5)的9号和491号构件在正式计算中表现为重要构件;试算过程中的579和419号待观察构件在正式计算中表现为重要构件,原因是其在正式计算中的基本效应标准差相对试算时有所减小,从而满足了式(5)的要求;试算过程的中的417号待观察构件在正式计算时基本效应的均值小于0.02,从而被判定为一般构件。

图5 试算基本效应计算结果(rs=20)Fig.5 Elementary effect results of trail calculation(rs=20)
对正式计算中判定为重要构件的491、419、579和9号构件进行构件重要性系数计算,其中μmax综合图6所示计算结果取为0.1,重要性系数结果如表1所示。

图6 正式计算基本效应计算结果(r=200)Fig.6 Elementary effect results of formal calculation(r=200)
由表1可知,重要构件内部的构件重要性排序为491、419、579和9号构件,其中491和419号构件构件重要性较为接近、579和9号构件的重要性系数较为接近。根据对称性,选取其他扇形区域内对应于491、419、579和9号构件的构件作为重要构件,则该网壳的重要构件如图7所示。由图7可知,该网壳中重要构件为主肋两侧5~7环范围内的斜杆和第一环环杆,共56根。

表1 重要构件的构件重要性系数Tab.1 Importance factors of important members

图7 重要构件结果图Fig.7 Distribution results of important members
3.1.3 与其他方法的对比
(1)基于拆除和基于损伤的构件重要性计算方法
基于拆除的构件重要性计算方法[10](简称为“拆除方法”)主要关注构件破坏对整体结构系统的影响,如在爆炸、撞击等意外偶然作用下结构中部分构件失效对结构整体刚度、稳定性和承载力的影响程度。此类方法常以构件失效导致的结构整体性能指标的损失率作为衡量构件在结构系统中重要性的评价指标,如:
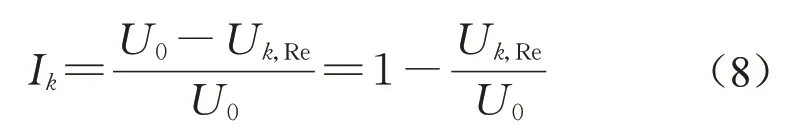
式中:Ik为第k根构件的重要性系数;U0为初始结构的整体性能指标;Uk,Re为第k根构件失效后的结构整体性能指标。初始结构是指所有构件都处于设计状态下的结构。
基于损伤的构件重要性计算方法[7](简称为“损伤方法”)则认为,实际结构一般不会发生构件由于某原因而完全破坏的情形。在定义构件损伤时,通常假定结构的损伤是结构局部刚度的损失,并将结构局部刚度的损失定义为单根构件横截面面积的降低,同时将构件截面面积的降低比例表述为构件削弱程度。损伤方法[7]以构件截面损伤前后结构性能指标的变化来衡量构件重要性,采用性能指标的折减系数作为构件重要性系数,其表达式与拆除方法相似,即:

与式(8)相似,式(9)中Ik为第k根构件的重要性系数;U0为初始结构的整体性能指标;不同的是,Uk,Da为第k根构件截面削弱后的结构整体性能指标。
综合式(8)和式(9)可知,拆除方法与损伤方法都是以构件失效或损伤后的结构整体性能的折减系数作为构件的重要性的衡量指标,两种方法的计算表达式相同,不同之处在于分析对象不同,前者针对构件失效这一极端事件,后者则针对实际工程中更为常见的构件损伤。
(2)三种方法计算结果对比
本节以网壳极限承载力为整体结构性能指标,分别根据拆除方法和损伤方法判定网壳的重要构件分布情况。为与本文方法所得的重要构件个数保持一致,拆除方法和损伤方法的重要构件个数均取为56。根据两种方法计算所得重要构件分布如图8所示。
由图7和图8可知:采用不同方法判定得到的重要构件分布存在较大差异。采用本文方法判定的重要构件为主肋两侧5~7环范围内的斜杆和第一环环杆;采用损伤方法判定的重要构件主要为主肋两侧3~4环范围内的斜杆和1~2环范围内的环杆;采用拆除方法判定的重要构件主要为3~4环范围内的主肋杆和2~3环范围内的环杆。

图8 不同方法的重要性构件分布情况(算例1)Fig.8 Distribution results of important members of different methods(Example 1)
重要性构件判定的准确与否可以通过对带缺陷网壳稳定极限承载力的估计准确与否来判断。对一特定的带有构件损伤的网壳,其全部构件的损伤程度记为D={D(1),D(2),…,D(N)},真实极限承载力记为f,若根据某方法判定得到的重要构件编号为m={m1,m2,…,mn},则推算网壳极限承载能力的过程如下:
(1)假定待检测网壳数值模型的构件损伤服从正态分布,其均值为μ(D),标准差为σ(D)。
(2)将所有重要构件m作为样本,抽取样本的“真实”构件损伤,记为d(m)={D(m1),D(m2),…,D(mn)}。
(3)计算样本的损伤均值μ(d)和标准差σ(d),并将μ(d)和σ(d)分别作为μ(D)和σ(D)的估计。
(4)根据正态分布假设,基于μ(d)和σ(d)随机生成所有未测构件的损伤,结合样本的已测数据,生成网壳全部构件的一个随机损伤D*。
(5)根据D*生成有限元模型,并计算网壳极限承载力的一个模拟值f*。
(6)根据蒙特卡洛方法,重复步骤(4)~步骤(5)进行s次模拟计算,可得到一系列f的模拟值,记为f*={f*(1),f*(2),…,f*(s)}。
(7)将f*的均值作为网壳承载力估计值;并将相对误差作为基于该重要性判定方法推算网壳承载力的平均误差。
对带有构件损伤D的网壳,分别基于本文方法、拆除方法和损伤方法得到的重要构件推算网壳承载力,可得到不同的承载力估计值向量
针对3.1.1节所述网壳,仍假定其截面面积降低比例d在区间[0,50%]服从均匀分布,并随机生成100种损伤模式D,假定每一种损伤模式对应一种真实的带构件损伤的网壳。对每一个带构件损伤D的网壳,分别基于本文方法、损伤方法和拆除方法得到的重要构件推算其网壳承载力,其中蒙特卡洛模拟[18]次数s取为30次。根据显著性检验[19]去除无明显差异结果后,本文方法与拆除方法的平均误差结果频数分布如图9a所示,本文方法与损伤方法的平均误差结果频数分布如图9b所示。

图9 平均误差频数对比图(算例1)Fig.9 Comparison of average error frequency(Example 1)
由图9可知,采用本文方法估算网壳结构承载力时的相对误差主要集中在[-0.05,+0.05],拆除方法的相对误差集中于[-0.15,0.15],损伤方法与拆除方法类似。与拆除方法和损伤方法相比,采用本文方法时,网壳结构极限承载力的估计误差更小,便于检测鉴定时准确把握结构真实性能。
3.2 算例二
为说明本文方法在其他尺寸网壳中的适用性,本节以一跨度为40 m、矢跨比为1/2的凯威特型单层网壳为例进行验证。该网壳结构环向划分为8个相同扇形曲面,径向分为6环,共169个节点和408根杆件。其他结构信息与算例一保持一致,详见3.1.1节。
限于篇幅,不再展示试算与正式计算过程中的基本效应结果。经本文方法验证,该网壳的重要构件如图10a所示(部分重要构件编号也标示在图中),重要构件数量为24,单个扇形范围内的重要构件的重要性结果如表2所示。根据拆除方法和损伤方法计算所得重要构件分布如图10b和图10c所示。其中由于重要构件数量的限制,拆除方法确定的重要构件未能保证中心对称。

图10 不同方法的重要性构件分布情况(算例2)Fig.10 Distribution results of important members of different methods(Example 2)

表2 重要构件的构件重要性系数(算例2)Tab.2 Importance factors of important members(Example 2)
根据3.1.3节所述方法,分别基于本文方法、损伤方法和拆除方法得到的重要构件推算其网壳承载力,去除无明显差异结果后,本文方法与拆除方法的平均误差结果频数分布如图11a所示,本文方法与损伤方法的平均误差结果频数分布如图11 b所示。由图11可知,采用本文方法估算网壳结构承载力时的相对误差主要集中在[-0.025,+0.025],拆除方法的相对误差集中于[-0.05,+0.05],损伤方法与拆除方法类似。与拆除方法和损伤方法相比,采用本文方法时,网壳结构极限承载力的估计误差更小。
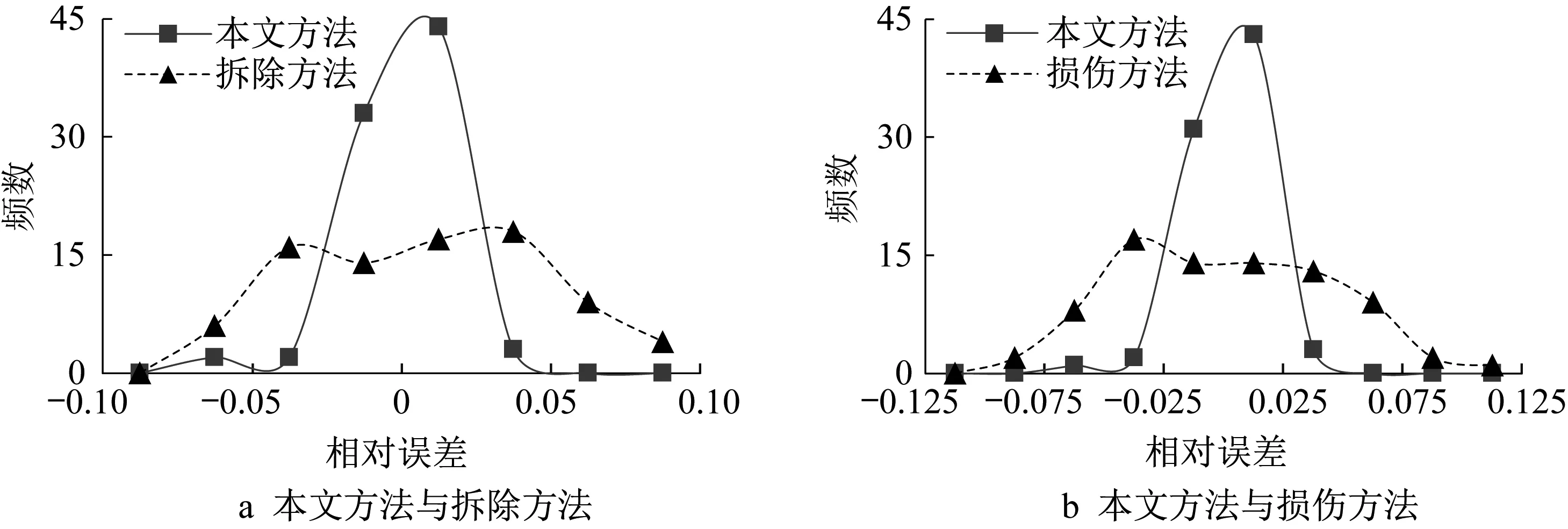
图11 平均误差频数对比图(算例2)Fig.11 Comparison of average error frequency(Example 2)
4 结论
传统的构件重要性分析方法仅提供局部的灵敏性分析结果,不能考虑所有构件共同变化对结构性能的影响。针对这一问题,本文提出了基于改进的基本效应法的构件重要性分析方法,并通过数值算例分析比较进行验证,通过研究分析,得到以下结论:
(1)本文将基本效应法应用于网壳结构构件的重要性判定,定义了适用于网壳结构的改进的基本效应。该定义考虑了所有构件损伤共同变化对结构整体性能的影响,物理意义明确,计算简便。
(2)基于改进的基本效应法的构件重要性分析方法分为试算、正式计算和重要性排序三个部分。其中试算与正式计算结合的双阶段判定方法可以准确判定重要构件和一般构件,并且有效减小了确定重要构件所需的计算量;重要性排序方法则有效解决了同时具有两个灵敏度测度指标的重要构件的相对重要性排序问题。
(3)基于拆除的构件重要性计算方法、基于削弱的构件重要性计算方法与本文方法的重要构件判定结果存在较大差异。算例结果表明,相较于其他方法,基于本文方法确定的重要构件进行抽样检测鉴定分析时,可以得到更为准确的网壳结构极限承载能力估算结果。
作者贡献声明:
栗云松:提出概念,有限元建模分析,论文撰写。
罗永峰:修改论文框架结构,指导数据分析,指导论文撰写。
郭小农:指导论文撰写。
张玉建:辅助有限元建模分析,修改论文。
