超大型船舶砰击颤振与波激振动研究进展

司海龙，顾学康，胡嘉骏

（中国船舶科学研究中心，江苏无锡 214082）

0 引 言

随着社会发展及航运的需要，商用运输船舶逐渐趋于大型化。到目前为止，出现了可运载超过24 000 TEU 的超大型集装箱船，30万吨大型油轮和40万吨超大型矿砂船也越来越多地穿梭在世界各大港口之间。随着运输船舶的大型化，其研发与设计也面临着越来越大的挑战。其中砰击颤振与波激振动是超大型船舶设计过程中必须要考虑的两个问题，砰击颤振对船体结构的影响主要体现在船体受到的极限载荷，过大的载荷会引起船体的屈服与屈曲破坏，而波激振动会大大降低船体结构的疲劳寿命。

集装箱船一般具有较大的球鼻艏、明显的外飘线型以及较为平坦的尾部线型，在恶劣的海况中航行时，由于艏底及艉底出入水、外飘区域与波浪发生碰撞等原因，船体会受到猛烈的砰击，进而引发剧烈的船体振动，该抨击振动称为砰击颤振。根据国内外实船试验及模型试验的研究成果，砰击振动弯矩甚至达到了船体总波浪弯矩的30%～40%。砰击颤振引起的高频振动弯矩与波浪诱导低频弯矩叠加时会对船体总纵强度构成严重的威胁。在集装箱船的发展历史中，先后发生了四次严重的海上事故，分别为1973 年的Nepthun Sapphire、1997 年的MSC Carla、2007 年的MSC Napoli 及2013 年的MOL Comfort，图1 和图2 分别为MSC Napoli 和MOL Comfort 集装箱船海难事故。经研究分析，引起后两起事故的一个重要原因就是砰击颤振。

图1 MSC Napoli号集装箱船海难事故[1]Fig.1 Accident of MSC Napoli[1]

图2 MOL Comfort号集装箱船海难事故[1]Fig.2 Accident of MOL Comfort[1]

超大型船舶的排水量和主尺度均较大，使得船体结构的柔性增大，波浪遭遇频率越来越接近船体湿模态振动频率。航行过程中，船舶极易发生波激振动，对船体疲劳寿命会构成严重威胁。大量研究表明，波激振动对船体疲劳损伤的贡献达到了40%～50%。目前国内外研究机构对波激振动进行了大量的模型试验研究，但很少涉及到线性波激振动及大开口船舶的扭转波激振动。

本文主要从波浪载荷、砰击颤振、波激振动三方面入手，对国内外的研究现状进行梳理，在此基础之上提出一些在该领域仍然需要深入研究的方向。

1 波浪载荷研究综述

砰击颤振与波激振动是船舶在波浪中航行时产生的两种特殊承载形式，其研究方法是一般波浪载荷研究方法的延伸与拓展，本章主要介绍一般波浪载荷的研究进展与现状。

1.1 波浪载荷试验技术研究进展与现状

对船体波浪载荷进行模型试验，一般是采用分段的船体模型，设计合适的测量梁模拟船体刚度，通过测量梁将各个分段连接起来，研究不同工况下船体波浪载荷传递函数及沿船长的分布，并且对船体波浪载荷进行统计分析，得到一定超越概率的极值。船模在波浪中的航行方式包含拖航和自航两种。根据试验的实际需求，测量梁有多种设计方式，在对扭矩的测量要求不高或只需测量垂向波浪载荷时，可采用多截面的圆管梁或方梁来模拟船体刚度[2-3]。对于特殊船舶，特别是大开口特征的集装箱船，为了模拟船体的扭转特性，研究人员在测量梁的设计方面开展了较多的研究工作，Zhu[4]采用一根横截面为方形的铝梁以模拟一艘长为290 m 的集装箱船的船体刚度，为了减小扭转刚度，在铝梁上方挖出了5个方孔，如图3（a）所示。Maron[5]为了能够更好地模拟集装箱船的刚度、一阶扭转、垂向弯曲、水平弯曲模态，设计并加工了一个上部开口的铝制U 型测量梁。在加工时，将该U 型测量梁尽可能地放在船的底部，使得船体U 型梁的剪心在船体基线以下，模拟船体梁水平弯曲与扭转之间的耦合作用。而Kim 等[6-7]则分别采用槽钢和工字钢模拟船体的刚度，如图3（b）所示。赵南[8]基于薄壁梁理论设计并加工了能够同时精确模拟超大型集装箱船垂向、水平、扭转刚度、剪心的U 型测量梁。在此基础上，司海龙[9]提出了通过U 型梁横剖面面内剪流获得波浪中航行时船体承受的扭矩的测量方法，如图3（c）所示。Grammatikopoulos[10]采用3D 打印技术加工制作了一艘驳船的弹性船模，其结构性能与S175集装箱船保持一致，在水池中开展了相关试验研究。除了采用测量梁模拟船体刚度以外，也有研究人员在船模中安装三角架，在船体分段处的三角架底部采用铰接的形式连接，三角架顶端用可调节刚度的弹簧相连，通过调节弹簧的刚度来模拟实船的刚度，同时在三角架安装测量力的传感器，测量得到的纵向力乘以距船模中和轴的高度便得到船体剖面受到的弯矩，对垂向力进行求和便得到船体剖面受到的剪力。Storhaug[11]与Drummen[12]便是采用该方法测量船体在波浪中航行时的波浪载荷。此外，Waskito[13]另辟蹊径，在一艘散货船模型外表面布满了压力传感器，在耐波性水池中开展模型试验，将船体湿表面的压力进行积分获得船体受到的波浪载荷，如图3（d）所示。

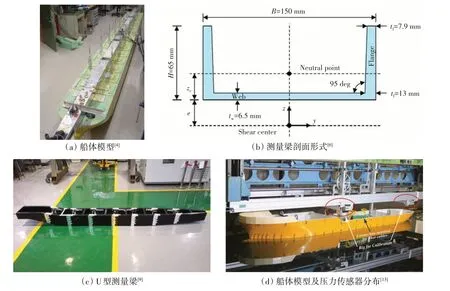
图3 不同试验的船体模型和测量梁Fig.3 Different ship models and backbones

耐波性水池试验可对规则波中波浪载荷传递函数、砰击颤振、波激振动、不规则波中波浪载荷统计特性开展全面深入的研究，且试验条件、试验周期可控，是应用最为全面和广泛的试验手段。但耐波性水池中波浪以长峰波为主，波浪形式对船舶特别是双体船、三体船等特殊类型船舶的砰击载荷有很大的影响，在耐波性水池中开展波浪载荷试验，无法真实地反映双体船、三体船的砰击载荷特性，如何在耐波性水池中实现真实的海浪环境条件，是值得深入研究的重要课题。

船模波浪载荷试验是一个复杂的系统工程，整个试验过程包括船模设计、加工、标定、重心和惯量的调整、正式试验、数据后期处理等多个环节，影响试验结果的因素非常多且复杂，为了确保试验结果的可靠性，需要对试验及结果开展不确定度分析。目前虽然取得了一定的研究成果[14-15]，ITTC、ISSC委员会也大力提倡该领域的研究工作，但船模波浪载荷试验不确定度分析仍然缺乏相关的理论基础与标准化的分析流程。

1.2 波浪载荷理论研究进展与现状

1.2.1 二维切片理论

波浪载荷理论研究取得了非常大的进展，从船体周围流场处理方法来讲，分为二维切片理论与三维面元法。二维切片理论起源于20 世纪50 年代，在70～90 年代得到了快速发展，其核心思想是通过引入“平面流假设”，将船体波浪载荷三维流动问题转化为船体剖面的二维流动问题，主要包括基于相对运动的切片理论、STF 法、新切片法等，经历了从刚体到弹性体、从频域到时域、从线性到非线性的发展过程，该方法具有计算效率高、计算稳定性强等优点。截至目前，二维切片理论仍然广泛地应用于船舶波浪载荷的预报工作中，由于篇幅所限，本文不过多论述。

1.2.2 三维面元法

早在20 世纪40 年代末50 年代初，便出现了三维脉动点源格林函数的表达式，但直到20 世纪70年代三维方法才开始应用于实际工程中。三维方法主要基于势流理论，包括自由面格林函数法和Rankine源法。自由面格林函数满足除物面条件以外的所有边界条件，只需在船体表面分布源或偶极来计算速度势。Rankine源法需要在船体湿表面、流体自由表面布置面元，计算效率偏低，但该方法适应性较好，可计及一些非线性因素对波浪载荷的影响。结合这两种方法的优点，Zhang[16]在1998 年首先提出了混合格林函数法的思想，通过一个假想的控制面将流场分割成内域和外域，在内域中布置Rankine源，在外域采用时域格林函数，内域和外域的速度势在控制面上相等作为连续条件，因为控制面是人为设置的，因此只需取简单的直壁面就可避免时域格林函数的振荡发散问题。

随着技术的不断进步，研究人员将适用于刚体的三维面元法扩展至求解弹性体运动及波浪载荷领域中，该方法主要包括两种思想，第一种是将势流理论与模态叠加法相结合的三维水弹性理论，基于势流理论计算船体受到的作用力，基于模态叠加法计算船体结构响应。吴有生院士[17]首先将三维势流理论与结构动力学相结合，提出了广义的流固耦合物面边界条件，该理论基于模态叠加法，适用于任意三维弹性体并能够分析结构的动响应。杨鹏[18]基于混合边界元法，结合模态叠加法，建立了基于内外场匹配技术的有航速船舶三维时域水弹性力学理论方法[19]，随后通过边界积分法和在流体内域自由面施加刚性边界，消除了三维水弹性频域求解中的不规则频率问题，并且建立了有限水深的三维时域格林函数水弹性计算方法[20]。陈占阳[21]基于Rankine 面源法及模态叠加法，考虑了由船体湿表面变化引起的非线性静水恢复力和入射力，按照动量砰击理论计算船体受到的砰击力，同时采用数值海岸避免反射波对计算结果的影响，引入PID自动舵模型解决了斜浪条件下船体运动发散问题。

第二种是基于隐式算法计算船体与周围流场的流固耦合问题。Kim[22]采用Newton法在时域中求解零航速船体与流场的流固耦合问题，分别得到流体域与船体结构的Jacobian 矩阵，代入船体表面压力与结构变形速度的联合方程求解船体结构响应，该方法属于隐式算法，可避免数值计算的不稳定性，相比模态叠加法，该方法无需进行小变形假设，可以扩展到求解结构的非线性问题。Kim[23]考虑船体弹性，采用高阶B样条Rankine源求解船体周围流场速度势，对船体结构进行三维有限元建模，采用隐式算法在时域中对流场压力及结构变形进行完全耦合计算。对船体进行三维有限元建模，不但可以准确地模拟船体的整体变形，还可以对船体复杂的局部结构进行有效模拟，例如集装箱船甲板大开口的模拟，可直接计算船体任意位置的结构响应。基于隐式算法求解船体与周围流场的流固耦合问题计算效率非常低。

由于在计算效率、计及流场三维效应及船体弹性方面的优势，在求解船体波浪载荷方面，三维面元法成为国际上的主流方法，在船舶与海洋工程领域获得了广泛的应用。由于船舶在大波高中以较高航速航行时，船体承受的波浪载荷具有极强的非线性，虽然国内外研究人员建立了多种可在一定程度上计及船体湿表面变化、砰击、上浪等非线性因素的计算方法，但由于这些非线性因素的复杂性，这些计算方法大多进行了某种简化，在势流理论范围内如何更加合理高效地计及这些非线性因素还需进行更加深入的研究。

1.2.3 CFD方法

由于CFD 方法可以计及湿表面变化、砰击、上浪、波面非线性、流体的粘性等非线性因素，属于全非线性求解，具有切片理论与三维面元法不具备的一些优势，因此将CFD同船体结构力学结合求解船体运动及波浪载荷成为一个趋势。该方法包括单向耦合和双向耦合，二者之间的区别就在于是否考虑结构变形对流体作用力的影响。Takami[24]基于STAR-CCM+和LS-DYNA，采用单向耦合的方式将有限体积法与三维有限元法耦合，计算了船体在波浪中的运动、砰击压力、垂向弯矩及局部结构响应，并对船体砰击颤振开展研究。 Lakshmynarayanana[25]基于商用软件STAR-CCM+和Abaqus，采用隐式迭代算法将水动力计算同船体结构响应计算相互耦合，船体刚度采用Timoshenko梁进行模拟，该方法属于双向耦合计算方法，图4（a）为甲板上浪发生时的水面变化情况。国内也有相关研究人员对该方法进行了深入研究，焦甲龙[26-27]采用双向耦合法对S175船的波激振动、砰击颤振、砰击、甲板上浪等现象开展了数值模拟，并验证了该方法的稳定性和可靠性，图4（b）～（c）分别为水动力网格与船舶在波浪中航行时的波面变化情况。Huang[28]考虑流体网格尺寸、时间步长、流域大小、流体粘性系数、船体单元数量等因素，对基于双向耦合算法的波浪载荷开展了不确定度分析，研究表明时间步长是影响计算结果特别是高频振动载荷收敛性的重要因素，在计算颤振等高频振动响应时，时间步长建议取为2节点振动频率的1/100，整体来看，时间步长引起的不确定度小于网格尺寸引起的不确定度。

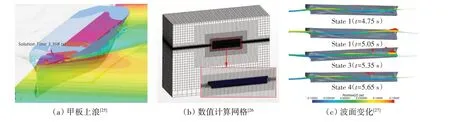
图4 液面变化及水动力网格Fig.4 Wave profile and computational grid

近几年，基于CFD 开展船体运动与波浪载荷的研究越来越多，也取得了一些骄人的研究成果，但由于该方法对计算资源要求较高，基于普通计算机的计算时间成本太过高昂，尚未大规模地应用于具体的工程研发项目中，如何提高该方法的计算效率是未来业内人员必须要考虑的一个重要方向。

2 砰击颤振研究进展与现状

2.1 试验研究进展

砰击现象及其引起的颤振是一种复杂的物理现象。近年来，国内外研究机构对砰击及颤振开展了一系列的船体模型波浪载荷试验。Ramos[29]通过对一艘集装箱船开展试验研究，将船体受到的垂向力分为4 部分，研究发现只有周围流场动量改变量对砰击压力及船体弯矩有重大影响。Dessi[30]通过对一艘高速渡轮的砰击问题进行试验研究，与传统结论不同，研究发现砰击的发生并非是相互独立的，而是有相关性的。砰击现象往往以群的方式出现，且在该时间段内，砰击发生的周期接近船体纵摇运动的周期。该种情况下，砰击引起的船体结构响应可能更具有威胁性，前一次砰击引起的船体振动还没结束，下一次砰击就开始发生了，前后两次砰击引起的船体振动可能会叠加在一起。Andersen[31]通过对一艘9400 TEU 集装箱船两年的实船测量数据进行分析，发现了相同的现象。Storhaug[32]通过对三艘集装箱船模型试验数据的研究对比发现，对砰击颤振来讲，相较船体主尺度，外飘入水角是一个更为重要的影响因素，航速次之。在评估颤振引起的波浪载荷时，需要考虑高海况条件下船体的主动减速及实际航行技术等因素。陈占阳[33]通过模型试验研究发现，砰击颤振与波高有着直接的关系，随着波高的增大，高频成分所占的比例越来越大，甚至接近于低频成分。通过模型试验研究还发现[34]，船体刚度越小，越容易发生颤振且颤振响应越大，相对于低频波浪弯矩，高频响应对浪向更为敏感，在横浪状态下，高频成分最小。焦甲龙[35]在葫芦岛港开展了大尺度模型试验，研究发现，不论是水平弯矩还是垂向弯矩，从船首到船中波浪载荷逐渐增大，但砰击引起的高频成分占比逐渐减小。砰击对船体载荷的影响明显大于对运动的影响。

由于砰击的强非线性，波浪载荷模型试验是研究砰击颤振最为可靠的方法和手段。试验表明，不同船型的砰击颤振特性有较大的不同，对于具有明显外飘的集装箱船或V型船，船艏外飘入水之后引起的周围流场动量变化对船体颤振的贡献更为明显，而对于底部较为平坦的油船，底部冲击压力对船体颤振的贡献则更为明显。

2.2 理论研究进展

研究砰击颤振的理论方法分为两种，一种是假设波浪诱导低频弯矩与砰击颤振弯矩是相互独立的。该方法中比较有代表性的是Baarholm 与Jensen 所进行的工作。Baarholm[36]认为波浪诱导低频弯矩服从三参数Weibull 分布，砰击颤振弯矩服从指数分布，对总弯矩进行三参数Weibull 分布拟合，采用等值线法对波浪载荷极值进行长期预报；研究发现中拱弯矩更容易受到砰击颤振的影响，提高航速会增强砰击颤振对波浪载荷长期极值的影响；不考虑低频弯矩与砰击颤振之间的相互影响，中垂弯矩会被严重低估，如果考虑二者之间的相互影响，砰击载荷对砰击颤振的影响会进一步增大。Jensen[37]提供了一种简单合理的设计导向型的极限载荷计算方法，该方法可用于船体概念设计阶段，输入条件只需船长、船宽、吃水、方形系数、艏外飘系数、船速及船体刚度。该方法将低频波浪诱导弯矩与砰击颤振引起的动弯矩分开考虑，并计及了二者之间的相位差；在计算低频波浪诱导弯矩时，考虑动量砰击引起的非线性因素，计及了中垂弯矩与中拱弯矩的不对称性；基于船体振动理论，求得底部和外飘区域与波浪发生砰击时产生的瞬态冲击力对船体结构振动响应的解析解，获得了波浪弯矩与砰击颤振弯矩之和超越某一极值的概率。

研究砰击颤振的另外一种方法即耦合法，该方法计及船体的弹性，将船体入水砰击计算方法嵌入到三维船舶波浪载荷计算程序中，在时域中计算船体波浪载荷及砰击颤振。Kim 将船艏划分为若干个二维剖面，将三维Rankine 面元法、三维有限元法及二维GWM 方法有效地结合起来，分别对10 000 TEU[38]和18 000 TEU[39]集装箱船的砰击颤振问题开展了研究，研究发现艏外飘产生的砰击力持续时间较长且较为平缓，艉砰击产生的砰击力持续时间较短且较尖，艏外飘砰击会使船体结构产生砰击颤振，但随后的艉砰击会削弱砰击颤振的峰值，同时波激振动与砰击颤振之间有相位差，这都在一定程度上削弱了砰击颤振的峰值，图5 为18 000 TEU 集装箱船的模态振型。Tuitman[40]与Malenica也采用同样的方法对船体砰击颤振进行了研究，图6 为计算砰击载荷时将船艏划分成的二维剖面。Moctar[41]和Oberhagemann[42]采用双向耦合法将Navier-Stokes 方程、非线性船体运动方程、线性的Timoshenko梁理论耦合起来，在每一时间步均考虑船体水动力与船体结构变形的相互影响，计算了三条集装箱船在波浪中的运动响应及波浪诱导载荷，成功模拟了船体波激振动及砰击颤振现象。焦甲龙[43]结合三维边界元法、梁理论、广义Wagner理论、溃坝理论开发了非线性时域水弹性理论，在瞬时湿表面上求解静水回复力、波浪激励力和辐射力，对规则波中船体运动响应和波浪载荷开展了理论与试验研究。研究发现，由于砰击作用船艏非线性较船中更为明显，船体为弹性时的砰击力小于船体为刚性时的砰击力，但与试验结果较为吻合。在恶劣海况中高速航行时，砰击颤振现象非常明显，波频载荷随着波高线性增大，但航速对其影响较小，高频载荷随波高和航速的增大均增大，但该方法只能计算顶浪状态下的砰击和甲板上浪问题。不规则波中[44-45]，船体运动时历曲线比较光滑，砰击对船体运动的影响比较小，砰击颤振现象非常明显，在船艏部位，高频载荷远大于低频载荷。由于砰击颤振的作用，中垂弯矩明显大于中拱弯矩。Jagite[46]用铁摩辛柯梁模拟船体梁，船中采用铰接形式，基于水弹塑性理论，对船体非线性砰击颤振特性开展了理论研究，研究表明，船体结构的非线性对砰击颤振响应影响较小。

图5 18 000 TEU集装箱船模态振型[39]Fig.5 Mode shape of 18 000 TEU containership[39]

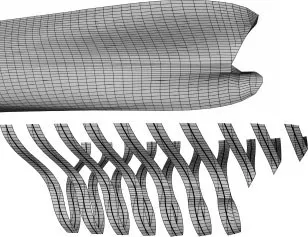
图6 计算砰击的二维剖面[40]Fig.6 2D sections for slamming calculation[40]

目前，耦合了基于势流理论的三维面元法、基于广义wagner理论的边界元法、模态叠加法的水弹性理论，是砰击颤振计算方面应用最为广泛的方法，该方法可计及船舶周围流场的三维效应，既可计算砰击引起的船体整体振动，又可计算局部砰击压力，且计算效率高，计算稳定性强。但目前的参考文献中呈现出的计算结果基本都是顶浪状态下的砰击颤振，该方法在斜浪中的应用还需要进一步的深入研究。

2.3 砰击颤振的影响

砰击颤振是砰击导致的一种瞬态性、突发性的船体振动现象。Prpic-Orsic[47]通过对23 名集装箱船船长的问卷调查发现，接近一半的船长表示遇到了砰击、颤振和甲板上浪。对于集装箱船来讲，船艉及艏外飘砰击会引起砰击颤振，砰击颤振往往发生在中垂状态。砰击颤振对船体结构的影响主要是增大了船体受到的极限载荷，Storhaug[48]通过对一艘8600 TEU 的集装箱船进行了船模波浪载荷试验，研究发现不论是中垂弯矩还是中拱弯矩，考虑砰击颤振时是不考虑砰击颤振的两倍以上。考虑砰击颤振时船体遭遇的波浪弯矩远远超过了IACS 规范计算结果，达到了IACS 规范计算结果的2.5 倍。在实船试验中也发现了类似的现象，Andersen[31]对一艘9400 TEU 集装箱船两年的实船测量数据进行了分析，研究发现，在船体发生砰击时刻，高频与波频引起的船体结构响应相当，对总响应的贡献各占50%。Barhoumi[49]对一艘8600 TEU 集装箱船的实船测量数据进行了分析，由于砰击颤振的影响，使得船艉1/4处的中垂和中拱弯矩均超出了规范值，其中中拱弯矩超出规范结果48%。Sumi[50]介绍了过去一百年由船舶断裂造成的海难事故的历史，指出过去船舶断裂主要发生在恶劣海况中的中垂状态，但在最近的集装箱船事故中，船体断裂发生在船体中拱状态下，因此需针对双层底结构集装箱船的屈曲失效及砰击颤振展开进一步的研究，并且制定相应的设计规范。IACS发布的URS11A规定，集装箱船必须考虑砰击颤振对船体强度的影响。另外，砰击颤振对船体疲劳强度也会产生较大的威胁，任慧龙[51]采用线性频域和非线性时域水弹性理论对集装船的疲劳损伤开展了研究，研究发现，与波激振动相比，砰击颤振会引起等量的甚至更高的疲劳损伤。由于砰击颤振对船体极限载荷的影响，对于超大型船舶特别是具有大外飘线型的集装箱船，在研发和设计过程中必须考虑砰击颤振对船体结构强度的影响。

3 波激振动研究进展与现状

3.1 试验研究进展

波激振动是一种波浪载荷持续激励下的谐振现象，主要对船体疲劳强度产生重要影响。比较典型的一个案例是一艘长为294 m的矿砂船[52]，该船航线是从圣劳伦斯港至鹿特丹港，航行不到一年，首先在舱口角隅处发现疲劳损伤，接着在纵向甲板纵骨的面板靠近肘板端部发现疲劳损伤，在随后几年的航行中，先后在甲板纵骨面板靠近防倾肘板的端部、甲板纵骨腹板加强筋端部、船底及舷侧纵骨与舱壁及肋骨框相交的端部分别出现了疲劳损伤。Storhau[53]对该船进行了实船长期监测与船模波浪载荷试验，经过对实船监测数据进行研究分析发现，在中级海况下航行，船体没有发生砰击，相应地也就没有砰击颤振发生，船体的高阶振动完全是由波激振动引起的。由于不断出现疲劳损伤，在2000 年对该船进行了维修及加强处理，将已经出现疲劳损伤的结构改换成尺寸较大的结构，船体剖面惯性矩及剖面模数增大了40%～50%，船体的湿模态振动频率增大了10%。Moe[54]对经过加强的矿砂船进行了长期监测，通过对监测数据进行研究发现，对船体结构进行加强之后，船体总的累积疲劳损伤有所降低，但波频及高频振动对疲劳损伤的相对贡献并没有多大影响。

当波浪遭遇频率等于船体湿模态振动频率时，一阶激励力的频率与船体湿模态振动频率相等，船体会发生线性波激振动。由于船体湿表面变化、船体对波浪的反射等会使船体受到二阶非线性激励力作用，在不规则波中船体还会受到二阶和频力作用，当二阶激励力的频率与湿模态振动频率相等时，船体还会发生非线性波激振动。在对294 m长的矿砂船波激振动进行研究时，Storhaug[55]认为引起船体振动的激励源分为四种，即船体航行引起的定常兴波、船体对入射波的反射作用引起的波面升高、船艏入水砰击及钝性船艏反射引起的二阶激励。在随后的40 万吨矿砂船船模波浪载荷试验中，进一步证明了上述观点，研究发现正是由于船体湿表面几何非线性、波浪的双向性及船艏对入射波的反射导致了船体发生二阶波激振动。顾学康[56]对船体的非线性波浪载荷的高阶谐振现象进行了试验与理论研究，通过对波浪弯矩时历曲线进行FFT变换，得到波浪弯矩的频谱图。当波浪遭遇频率为船体湿模态振动频率的1/n时，频谱图存在多个峰值，分别对应波浪遭遇频率、船体湿模态振动频率与高阶谐振频率，此时并没有观察到有砰击现象发生。文中认为由于船体线型为非直壁，船体已不再是一个线性系统，船体大幅运动时，会产生非线性的水动力，进而产生高阶谐振的波浪载荷，高阶谐振的能量随波高的增大而增大。汪雪良[57]以一艘油轮为研究对象开展了波激振动模型试验，研究发现，由于波动压力随水深指数衰减，波激振动更易在压载状态下发生。中大波高下，波浪载荷的非线性现象加剧，压载状态下非线性影响较满载时的大，高频振动响应可达垂向总载荷的20%～30%。船体结构刚度减小，不仅使船体垂向振动频率减小，同时倍频对应的载荷响应增大，波激振动现象更加明显[58]。Tang[59]对集装箱船在恶劣海况中的非线性波浪载荷特性开展了模型试验研究，为了更好地模拟船体振动模态，测量梁为变截面梁，研究发现，升沉和纵摇运动随波高增大呈线性增大，垂向弯矩的非线性主要体现为高频谐振，高阶谐振对中垂弯矩的影响大于对中拱弯矩的影响。通过船模波浪载荷试验，波激振动特性大体上表现为如下几个特征：由于波浪激励力降低的原因，相比压载状态，满载状态时船体波激振动有所降低，对船体疲劳的影响也有所降低；航速越高，波激振动越明显；在顶浪及首斜浪海况下，波激振动最为明显，随着浪向角逐渐从顶浪向横浪变化，波激振动现象逐渐降低，但在随浪海况下，波激振动也较为明显；对于不规则波，平均跨零周期越小，船体波激振动现象越明显；波高越大波激振动也越明显。

虽然研究人员对船体波激振动开展了大量的模型试验研究，但很少有参考文献提到超大型船舶的线性波激振动及超大型集装箱船的扭转波激振动模型试验。开展线性波激振动需要满足波浪遭遇频率与船体一阶湿模态振动频率相等这一苛刻的条件。在船舶主尺度及结构剖面特性确定的情况下，有三种途径可以满足该条件：（1）在合理的范围内尽量增大船模的航速，提高波浪遭遇频率；（2）降低缩尺比，增大分段式缩尺船模的主尺度，降低船模自身的一阶湿模态振动频率；（3）减小入射波波长，提高波浪遭遇频率。但由于船模航速的提高需在其最大航速范围之内，耐波性水池所能容纳的船模的主尺度也有一定限度，入射波波长越短，越容易形成碎波。正是由于这三个条件的限制，开展超大型船舶波激振动模型试验非常困难，其研究成果也是非常的少。由于超大型集装箱船的大开口特点，使得其湿模态扭转振动频率小于垂向弯曲振动频率，且剪心位于船体基线以下，如何设计并加工可同时模拟船体垂向、水平、扭转刚度及剪心的测量梁、如何建立适用于该种测量梁的扭矩测量方法是超大型集装箱船扭转波激振动模型试验能够得以顺利开展的关键所在，这也使得目前有关超大型集装箱船扭转波激振动的水池模型试验非常的少。

3.2 理论研究进展

最近越来越多的理论研究将其重点放在二阶波浪激励力对波激振动的影响上，根据实船测试结果，发现船体航行期间，遭遇到的波浪并非向同一个方向传播，而是存在多个传播方向，Vidic-Perunovic[60]基于非线性二阶切片理论对一艘矿砂船波激振动现象进行了理论研究，不但考虑了单一浪向不规则波非线性自由表面条件引起的非线性二阶力，同时也考虑了具有不同浪向不规则波之间的相互耦合作用产生的非线性二阶力。对于船中弯矩，波频部分主要与线性激励有关，而高频部分主要与非线性的二阶激励有关。当两个不规则波方向几乎相反时，波激振动最为明显，高频振动响应是波频响应的3.7 倍，二阶相互耦合项对船体高频振动的贡献非常突出，且二阶压力项不随与静水面距离的增大而减小。当浪向较为接近时，二阶相互耦合项的作用相对较小。线性理论和不考虑不同浪向相互耦合的一阶非线性理论严重低估了船舶的波激振动，考虑了不同浪向相互耦合的二阶非线性理论大大提高了船体波激振动的预报结果。在其博士论文中，对波浪之间的夹角对波激振动的影响进行了分析。航行过程中船艏兴波也会引起二阶激励力，可能也是重要的波激振动激励源。在以后的研究中，Vidic-Perunovic[61]又将深水二阶非线性水弹性切片理论进行扩展，使之能够计算有限水深中船体的波激振动，研究发现，水深是影响船体波激振动的一个重要因素。为了避免对高阶导数的求解，Shao[62-63]基于三次形状函数，在随船坐标系中建立了高阶边界元法，对一艘改进的Wigley 船的二阶波激振动在时域中开展了数值研究。研究发现：船体二阶绕射激励力远大于伯努利方程中的速度势的平方项，短波情况下，航速越高，二阶绕射激励力越大；对于肥大型船舶，二阶绕射激励力大于细长体船舶；压载状况下，二阶波浪激励力大于满载状态。Heo[64]基于高阶边界元法研究了弹性体在双色波中的二阶水动力与响应，为了求解边界值问题，边界积分方程采用自由面格林函数，并用二次形状函数进行离散，边界法向考虑了船体运动及弹性变形。段文洋[65]基于泰勒展开边界元法对波浪航行中集装箱船的船体运动和波浪载荷开展了数值研究，研究发现，航速对船体运动与载荷具有显著的影响，随着航速的增大，二阶波浪力越发显著。Hanninen[66]以一艘约300 m 长的游轮为研究对象，采用RANS-VOF方法，对引起波激振动的二阶谐振波浪载荷在纵向及垂向的分布进行了研究。研究发现：船艏部位引起的二阶波浪激励力对总的二阶波浪激励力的贡献最大，船艏会对附近波浪的生成具有重要的影响；研究船体的波激振动现象，需考虑船体的三维绕射问题；当某处的二阶波浪激励力较大时，则该处总的波浪激励力升高时间比衰减时间要短，会形成一种冲击效应，航速越高、波高越大，这种现象越明显，对船体的波激振动会产生重要的影响。

为了更好地基于模态叠加法对船体波激振动开展数值研究，研究人员从测量梁的模态振型入手开展了相关工作。Hong[67]为了研究船体的水弹性响应，基于勒让德多项式和切比雪夫多项式代替铁摩辛柯梁的干模态，尽管这种方法不满足边界条件和不具备一定的物理意义，但仍通过模态展开法验证了这些正交函数的叠加可以模拟船体梁的弹性变形。Riesner[68]采用一维梁模拟船体刚度，基于模态叠加法，用14 个自由度描述一维梁单元的两个节点的位移和变形，可同时计及船体的垂向、水平、扭转变形，考虑入射波、船体运动及变形引起的船体湿表面变化等非线性因素，对超巴拿马型集装箱船在斜浪中的波激振动开展理论研究，图7为定义一维梁单元两个节点位移和变形的坐标系统。

图7 梁单元坐标系统[68]Fig.7 Coordinate system of a typical beam element[68]

以上研究人员采用非线性切片理论、不同高阶边界元法对船体承受的高阶激励力开展了理论研究，在一定程度上反映了船体的波激振动特性，但由于船体湿表面变化、波浪非线性、船体对波浪的辐射和绕射，其非线性激励源非常复杂，且超大型集装箱船的扭转波激振动始终未引起研究人员的广泛关注，现有的势流理论与水弹性计算方法还需要进一步的完善和发展。

4 总结与展望

综合上述研究情况，国内外研究人员对船体砰击颤振与波激振动进行了大量试验与理论研究，但对砰击颤振进行理论研究时，大部分采用的是基于广义Wanger理论的二维边界元法。由于试验条件的限制，对超大型船舶线性波激振动的研究比较少，且由于集装箱船具有大开口的特点，在斜浪中航行时除了发生垂向波激振动，还有可能发生水平及扭转波激振动，不论是试验研究还是理论研究，关于这方面的参考文献都非常少。为保证船模波浪载荷试验的可信度，还需对试验进行不确定度分析，给出一定置信水平条件下的置信区间。未来对超大型船舶的砰击颤振及波激振动的研究可从以下几个方面开展：

（1）对船模波浪载荷试验的不确定度进行分析，给出一定置信水平条件下的置信区间；建立船模波浪载荷试验的不确定度分析的相关理论基础与标准化流程。

（2）研究如何在耐波性水池中实现真实的海浪环境条件，在该环境条件下对双体船、三体船等特殊类型船舶的局部砰击压力和整体砰击颤振开展模型试验研究。

（3）在势流理论范围内，开发可精确、高效求解顶浪、斜浪条件下船体入水砰击的计算方法，并将其与三维水弹性理论进行有机结合，对船体砰击颤振进行理论研究。

（4）突破试验条件的限值，开展船舶大尺度模型试验，对船体线性波激振动开展研究。开发可同时精确模拟集装箱船垂向、水平、扭转刚度、剪心位置的测量梁及适用于该种测量梁的扭矩测量方法，对船体垂向、水平及扭转波激振动开展模型试验研究。

（5）从引起船体波激振动的激励力入手，研究线性与非线性激励力对船体波激振动的影响。

（6）研究砰击颤振对船体结构强度的影响及砰击颤振作用下船体结构承载能力的安全裕度。

（7）加大基础计算能力的建设，实现CFD在波浪载荷数值计算领域的大规模应用。