基于ABAQUS 的飞机起落架扭力臂的拓扑优化
2022-12-01丁超杰
丁超杰
(200093 上海市 上海理工大学 机械工程学院)
0 引言
飞机起落架是飞机在地面停放、滑行、起飞着陆滑跑时用于支撑飞机重力、承受相应载荷的装置[1],其功能将直接影响飞行安全。对于飞机起落架的结构设计,在满足必要刚度的前提下,应尽可能减轻质量。然而,去除零件哪个部位或多余部分并非易事,之前往往采用耗时且代价昂贵的实物测试方法,但就结果而言,通常并不理想。本文采用ABAQUS/CAE 对其进行拓扑优化,以满足轻量化的设计需求。
拓扑优化是一种根据给定的负载情况、约束条件和性能指标,在目标区域内对所给零件进行优化的数学方法。总之,是基于条件(如应变能最小)找出相应参数最优良(如刚度)的拓扑结构。针对起落架的分析优化,许多学者已经进行了相关研究。于方圆[2]等利用AMESim 对前起落架收放系统建模,对其放下过程系统压力及作动筒行程变化进行分析;齐浩[3]等以无人机半轴式主起落架和半摇臂式后起落架作为研究目标,分别建立包含模拟飞机等效气动升力造成载荷变化的阻尼及缓冲支柱摩擦力的主起落架降落震力学分析模型,建立数字化样机进行联合仿真,研究其着陆动态特性;石磊[4]等基于ANSYS Workbench 对扭力臂进行应力应变分析,通过MATLAB 对重构模型的7个显著参数进行响应面建模,并用遗传算法获得其结构尺寸的优化;徐浩然[5]等以飞机起落架的外筒结构作为研究对象,以轻量化为目标建立拓扑优化数学模型,并在此基础上以应力最小作为优化目标,建立起自由曲面形状优化模型,获得了最优的解决方案。
本文针对飞机起落架结构,以应变能和体积为设计变量建立目标函数,考虑到工业生产中的脱模工序几何限制,利用ABAQUS/CAE 中的条件算法进行拓扑优化,并与优化前结构进行对比,旨在保证起落架机构刚度的同时实现轻量化的选择。
1 拓扑优化设计
拓扑优化的目的是完成结构轻量化设计,具体过程是将目标区域离散成大量的子集,并对这些子集进行应力强度分析,再按某种优化策略或准则(即目标函数和约束)从这些子集中删除部分材料,用保留下来的子集描述最优化的拓扑结构。一般通用求解过程如图1 所示。优化计算的过程主要为设计响应、给出目标函数、设置约束和几何限制、创建停止条件。
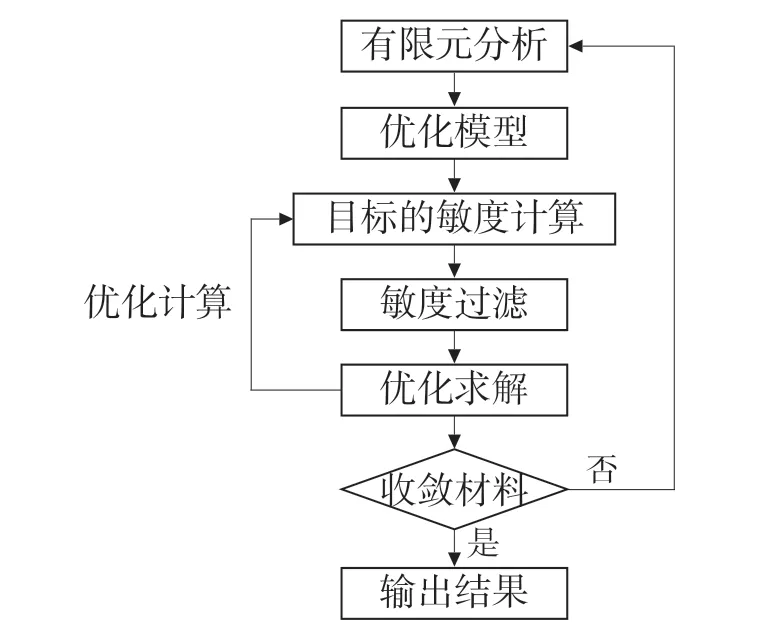
图1 拓扑优化流程图Fig.1 Topology optimization flow chart
在对结构拓扑优化时,过程中应该考虑应力约束、位移约束和最小构件尺寸约束的综合优化问题[6],可以描述为
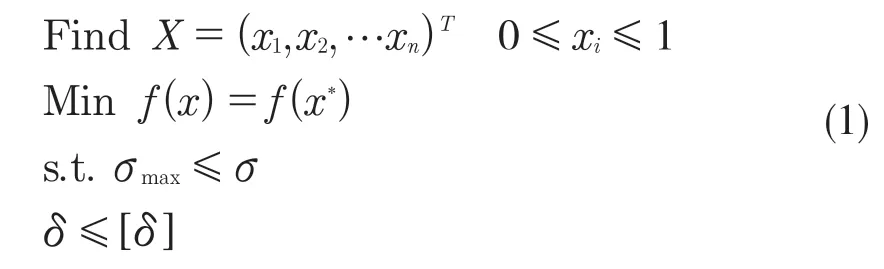
式中:X——拓扑优化变量;xi——材料相对密度;f(x)——目标函数;x*——优化结果的最值变量;σmax——单元最大应力;σ——许用应力;[δ]——位移约束的上下限最值。
2 有限元模型建立
飞机起落架扭力臂主要受扭矩作用,飞机起转状态下扭力臂受扭矩最大[7]。本文部件所用材料为Ti,弹性模量为114 GPa,泊松比为0.34。飞机起落架装配示意图如图2 所示。
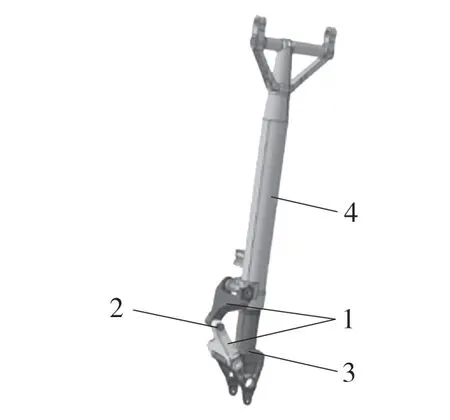
图2 飞机起落架装配示意图Fig.2 Schematic diagram of aircraft landing gear assembly
当飞机起落架工作时,上下悬架会发生相对位移(飞机降落时)或相对扭转(飞机在地面转弯时),这2 种情况都会对扭力臂产生不同的加载,因此当对扭力臂进行结构优化时,需要对这2 种加载情况进行相应的设置。
本文利用SolidWorks 建立三维模型,并将图3所示的有限元模型导入装配,在两端施加2 个运动耦合约束,连接销部分连接单元的刚体约束,扭力臂和连接销定义相互接触。
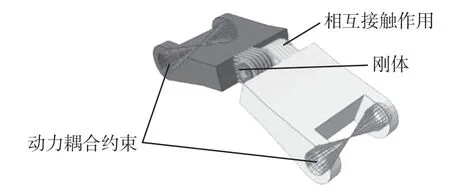
图3 有限元模型Fig.3 Finite element model
载荷加载如图4 所示,加载方向1 的集中力为3.3×105N,加载方向2 的扭矩为6.3×106N·m,网格划分将零件分割后使用线性、缩减积分的三维应力单元(C3D8R),划分的边种子在优化目标区域可以适当密集。如果网格太粗糙,会使计算的结果应力不准确从而影响优化结果,本文选择按尺寸划分,数值为2。
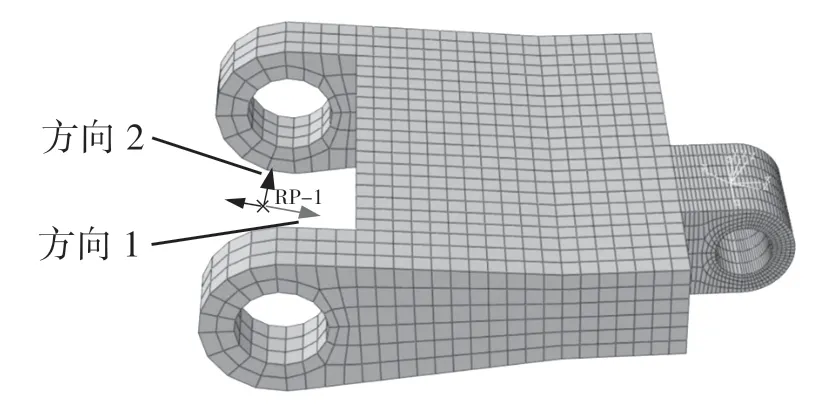
图4 载荷施加及网格划分Fig.4 Load application and meshing
3 建立拓扑优化
3.1 建立设计响应
设计响应是为定义目标或约束而创造的参数。基于条件的优化问题的原理是最小化模型结构的柔度以便最大化其刚度(两者互为倒数关系)。优化区域中单个单元的应变能的总和作为度量模型结构柔度的参数,通过最小化总应变能来提高优化结果的刚度。
本文选用应变能和体积为设计响应,选择整个模型作为优化区域。应变能即是结构的柔度,是零件结构的柔性和刚性的度量,其线性表达式为

式中:u——位移变量;k— —整体刚度矩阵。
体积是设计区域内所有单元体积之和∑Ve,其中Ve为单元的体积。
3.2 创建目标函数
拓扑优化的任务目标是在相对体积约束0.5(去除50%的相对体积)的条件下,使设计区域的最大应变能最小化(相当于最大化刚度),同时考虑实际生产限制。因此,优化模块中目标函数满足:(1)扭力臂刚度在关键加载步中最大;(2)总应变能在关键加载步中最小;(3)体积约束为Vfinal≤0.5Vinitial;(4)RP1 点的1 轴的旋转自由度约束,如图5 所示;(5)非优化区域的限制;(6)制造工艺的限制。
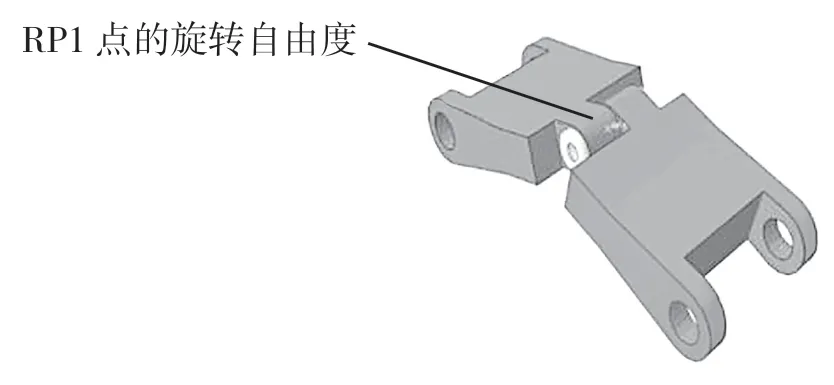
图5 连接销部分固定Fig.5 Connecting pin partially fixed
本文采用相对密度法,以应变能最小(即结构柔度)为目标函数,0.5 倍优化后体积为约束条件创建数学模型。
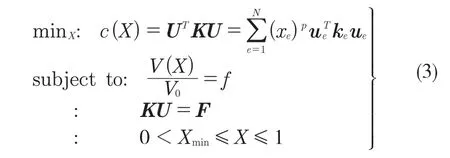
式中:X——设计变量,X={x1,x2,…,xi,…,xN},本文为应变能和体积,为防止应力奇异,其最小值略大于0;N——单元总数;F——整体荷载矩阵;U——位移矩阵;K——整体刚度矩阵;Ue——单元位移矩阵;Ke——单元刚度矩阵,施加载荷及边界条件后均由ABAQUS 得出;f——体积系数,本文为0.5;V(x)——优化后的材料体积;V0——初始材料体积;p——惩罚因子,一般取3。
3.3 创建约束
设置约束(Manufacturing Constraint)。在Name选项中选择volume,并在A fraction of the initial value选项中将约束定为0.5,单击OK 按钮完成设置。
3.4 建立几何限制
几何限制是对拓扑优化问题的额外约束,使得优化更加切合实际。如果不设置几何限制,一方面,拓扑优化结果可能无法使用常规的生产技术制造;另一方面,添加几何限制也能得到工件所需的对称性或尺寸大小的约束等。
同时,为了在模型中保持原始的设计意图。即通过扭力臂与连接销(通过建立的运动耦合模型)将负载从一端传输到另一端,需要固定载荷所施加的区域。而在建立设计区域时,选择了整个模型作为优化区域,所以本节会在几何限制中进行相应设置,以对载荷加载区域强制保持约束(即不会被优化器所改动)。
3.4.1 固定载荷区域
为使优化切合实际,需对部件的非设计区域进行固定(冻结),以保证优化后的部件符合实际工况。如图6 所示,对图中黑色区域进行固定约束。
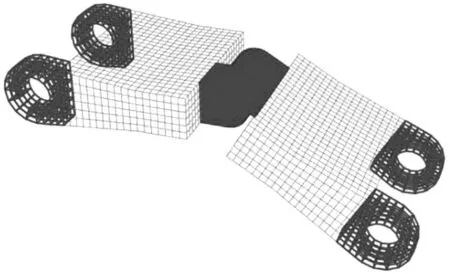
图6 冻结区域Fig.6 Frozen area
3.4.2 分模面几何限制
为了确保最终的设计方案可以使用相应的成型技术制造,需要对优化进行特定的中心平面几何限制(即分模面限制),并通过指定脱模区域、拉动方向和位于脱模面上的点确定。图7 中黑色区域为脱模面,另一半的操作与图7 相同。
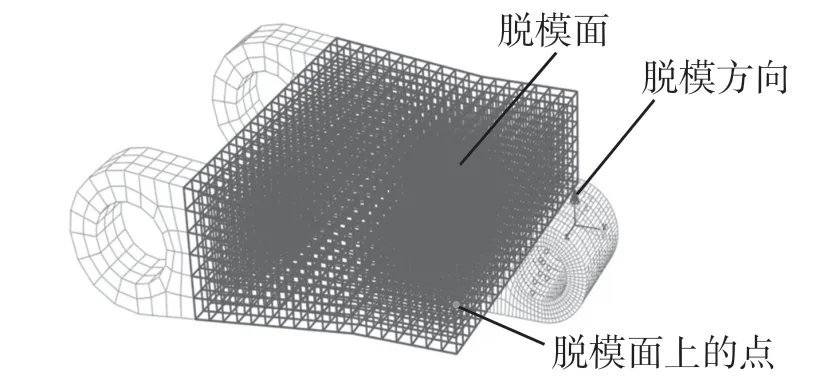
图7 脱模面限制Fig.7 Limit of demoulding surface
3.4.3 对称几何限制
对称几何限制旨在简化模型的优化结果,便于生产,保证起落架部件两端零部件变形相同。图8 中黑色部分即为对称几何限制区域。

图8 对称几何限制区域Fig.8 Symmetrical geometric restriction region
3.5 停止条件
停止条件即优化分析的最大迭代次数,会在每次迭代中检查最大迭代次数是否达到或者是否收敛到了优化的结果。ATOM(拓扑优化模块)会提供整体和局部停止条件,一般局部条件很少需要用到。ATOM 的默认设置如表1 所示,本文采用拓扑优化默认最大迭代次数,即迭代次数为15。

表1 默认最大迭代次数Tab.1 Default maximum number of iterations
4 拓扑优化结果分析
在可视化模块中查看优化结果,首先需将优化结果组合(Combine)到一个输出文件中(odb),在特殊条件下,为减少输出数据库文件的大小,只需保留第一个和最后一个设计周期的分析结果。对于分析结果,只需在优化期间保留模型中的应力和位移,即场输出变量S(应力)和U(位移)。
优化前和优化后的应力结果如图9 和图10 所示。由图9 和图10 可知,优化前的应力各项数值均大于优化后的结果。优化前应力最大值为3.523e3 MPa,优化后应力最大值为3.379e3 MPa。

图9 优化前的应力云图Fig.9 Stress diagram before optimization

图10 优化后的应力云图Fig.10 Optimized stress diagram
优化后应力最大值下降了4.09%,说明优化后在满足基本刚度的条件下,零件应力最大值有所下降,满足设计要求。优化前后体积的变化如图11和表2 所示。图11 指向曲线即为体积变化曲线,由图11 可知,体积在15 次循环中不断减少,由表2 可得,最终优化体积为2.568 298 8e+7 mm3,较初始体积下降了49.15%,实现了起落架轻量化设计需求。
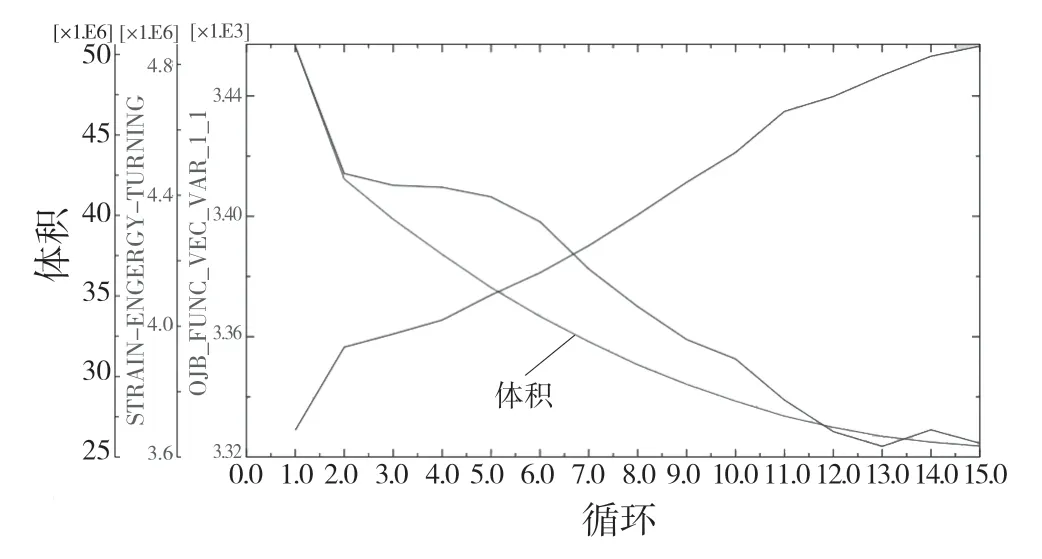
图11 体积约束曲线Fig.11 Volume constraint curve

表2 体积优化数据Tab.1 Volume optimization data
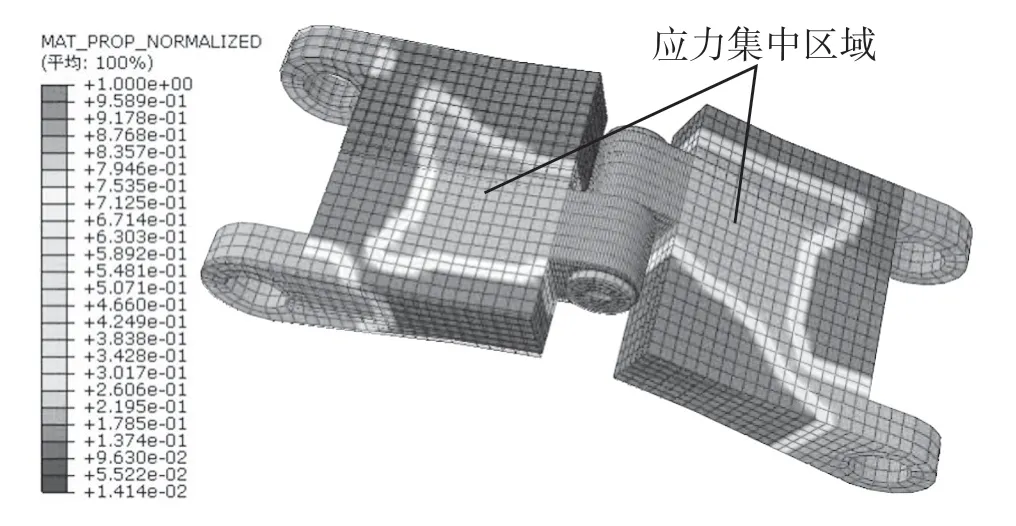
图12 AVG 为100%下的优化结果Fig.12 AVG as the optimization result at 100%
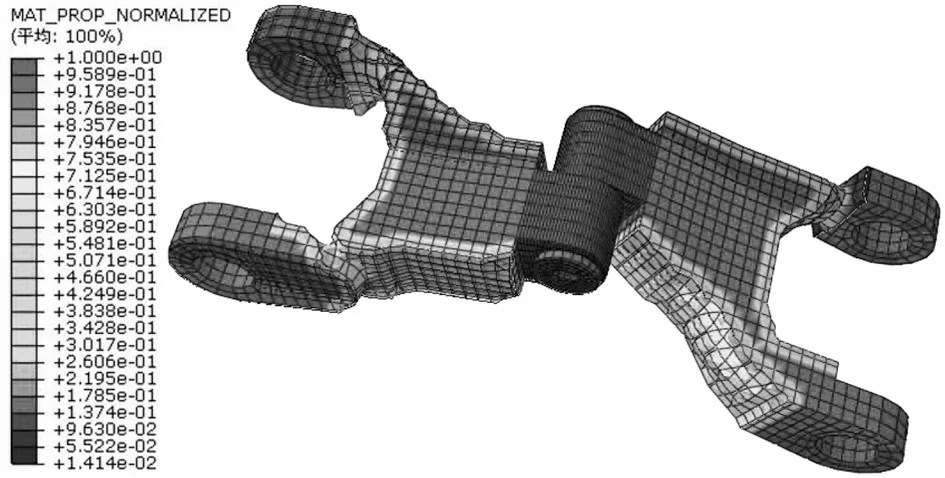
图13 优化结果的相对密度分布Fig.13 Relative density distribution of optimization results
5 结语
本文基于飞机起落架工作状态的载荷,对其扭力臂进行拓扑结构优化。在满足基本设计需求与制造工艺要求的情况下,结构总体积较初始下降了49.15%,最大应力下降了4.09%,得到了轻量化的模型方案。因此,拓扑优化结果对飞机起落架的分析具有重要的工程价值和实际指导意义。
