基于自适应蚁群算法的医疗资源应急优化调度模型设计
2022-12-01赵宏业
赵宏业
(河北北方学院附属第二医院,河北 张家口 075100)
近年来,突发性大型公共卫生事件的频繁发生,给社会发展与人民健康带来了严重威胁。在突发事件发生后,如何快速建立高效、合理而且科学的医疗资源管理体系,并有序、合理地开展医疗资源应急调度,对于控制疾病传播和保障人民生命安全具有重要意义[1-3]。
医疗资源应急优化调度是通过合理安排医疗资源的分配及车辆运送的路径,在最短时间内、最大程度地满足应急点的医疗资源需求[4-7]。这是一个高维度、非线性的数学规划问题,该问题的求解通常需要借助计算机技术和人工智能算法。蚁群算法(Ant Clony Optimization,ACO)是一种模拟蚂蚁种群觅食机制的启发式算法,其在路径优化调度方面的应用较为广泛[8-10]。但传统蚁群算法存在搜索能力差、易陷入早熟及求解速度较慢等缺点[11-12],因此无法适应医疗资源应急优化调度对求解算法的需求。
针对此问题,提出了改进的自适应蚁群算法,对应急调度模型进行快速求解,从而保障了医疗资源优化调度的准确性与及时性。
1 医疗资源应急优化调度模型设计
1.1 优化目标函数
医疗资源应急优化调度模型的优化目标包括两个:一是应急需求点接收到医疗资源的满意度最大;二是医疗资源运送时间最短,因此优化目标函数叙述如下:
1)优化目标f1如下所示:

式(1)中,f1为应急需求点接收到医疗物资的满意度;αjh和λjh分别为第j个应急需求点对第h种医疗资源(包括物资和人力)的紧缺程度与满意度;X、W则分别为应急需求点及医疗资源的集合。
第j个应急需求点中第h种医疗资源的紧缺程度计算方式如下:
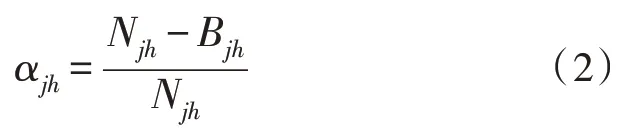
式(2)中,Njh和Bjh分别为第j个应急需求点对第h种医疗资源的总需求量与已储存量。第j个应急需求点第h种医疗资源紧缺程度λjh的计算方法为:

2)优化目标f2如下所示:
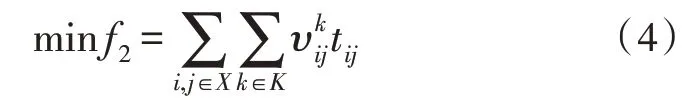
式(4)中,f2为医疗资源运送时间;为式(4)的布尔变量,表示第k辆运送车的行驶路径是否包含从第i个医疗资源供应点到第j个应急需求点的路径,若包含则=1,否则=0;tij为第i个医疗资源供应点到第j个应急需求点路径的行驶时间。
3)多目标处理方法。针对上述两个优化目标,文中采用加权法进行处理,得到归一化的优化目标函数如下:

式(5)中,ω1和ω2分别为优化目标f1与f2的权重系数;分别为优化目标f1的最大值及最小值;分别为优化目标f2的最大值和最小值。
1.2 约束条件
1)车辆最大运送容量约束。运送车辆承载的医疗资源容量应不超过其自身最大的运送容量,即:
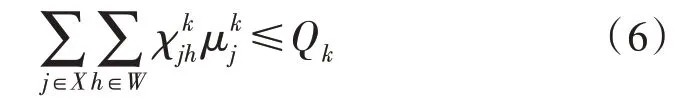
式中,Qk为第k辆车的最大运送容量;为式(6)的布尔变量。当第k辆车经过第j个应急需求点时,=1,否则=0。
2)车辆运送路径约束。车辆运送路径应满足以下3 个条件:①车辆路径到达某个应急需求点后,应从该应急需求点出发前往下一个目的地;②每个应急需求点仅有一辆车到达并提供医疗资源,以提高运送效率;③出发和返回的运输车辆数应一致,且小于可用车辆总数。
以上3 个约束条件表示如下:
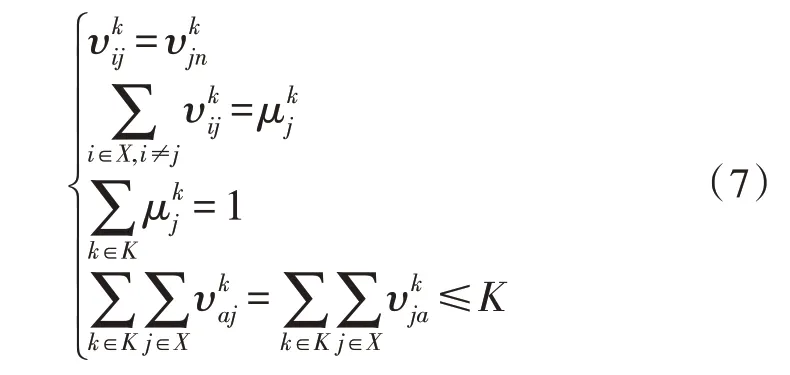
式中,a为应急供应点。
3)其他约束。运送车辆在应急需求点提供的医疗资源容量应小于该点的剩余需求量,即:

2 基于AACO算法的优化调度流程
2.1 传统蚁群算法
在典型蚁群算法中,第m只蚂蚁从应急需求点i转移到应急需求点j的概率为[13]:
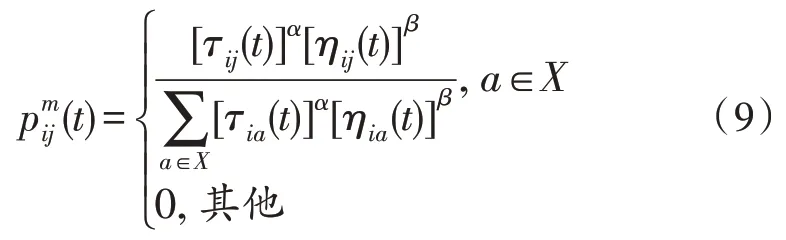

从应急需求点i到应急需求点j路径上的信息素浓度计算方式如下:
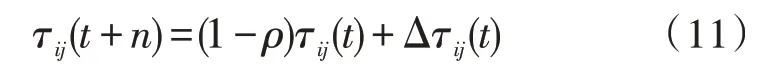
式中,ρ为挥发系数,Δτij(t)为所有蚂蚁从应急需求点i到应急需求点j路径上留下的信息素总量,其计算方法如下:


式中,Lm为一轮迭代中第m只蚂蚁经过路径的总长度;Q为所有蚂蚁的信息度总量,是一个正值常数。
2.2 自适应蚁群算法
针对传统蚁群算法存在易陷入局部最优且收敛速度较慢等不足,提出一种自适应蚁群算法(Adaptive Ant Colony Optimization,AACO)[14-16]。AACO 采用分组搜寻策略,将蚁群分为G组,并对转移点选取策略及信息素更新策略均进行了改进:
1)改进转移点选取策略。针对传统蚁群算法容易陷入局部最优解的问题,提出了融合确定性与随机性的应急需求点转移策略,需求点的具体计算方法为:
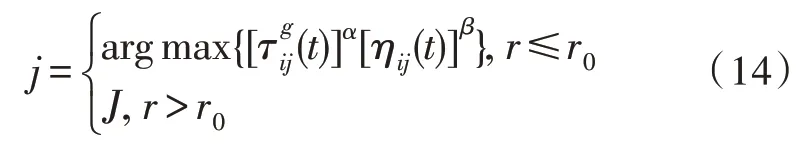
2)改进信息素更新策略。为了提高蚁群的搜索能力与效率,提出了融合多种更新方法的信息素更新策略。第m只蚂蚁完成一轮迭代后,采用局部信息素更新策略:

式中,σ为局部信息素挥发系数,τ0为取值较小的固定常数。当所有蚂蚁完成一轮迭代后,采用全局信息素更新策略:

式中,Lg为第g组蚂蚁的最优路径长度;ρ(t)为全局挥发系数,其采用自适应函数计算,可表示为:

当所有分组蚂蚁均经过R轮迭代后,采用基于分组交流的信息素更新策略:

式中,ε为各组间交流信息素挥发系数;Lg,best为所有分组蚂蚁的最优路径长度。
基于AACO 算法的医疗资源应急优化调度模型求解流程如图1 所示。
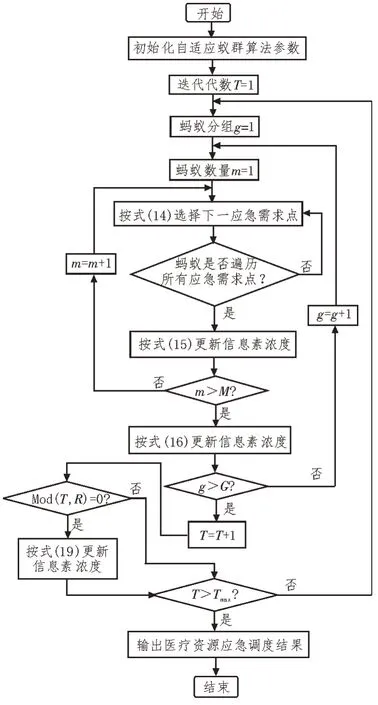
图1 模型求解流程
3 算例分析
假设某区域出现突发事件,应用所提算法进行医疗资源应急调度,以验证所提算法的正确性与有效性。
3.1 基础数据设置
AACO 算法的参数设置如下:信息素系数α=1、期望系数β=5、蚂蚁种群数量M=80、蚂蚁分组数G=10、信息交流代数R=20、局部信息数挥发系数σ=0.1、全局信息素挥发系数ρ=0.1、最大迭代次数Tmax=500。假设运送车辆的总数为7,并根据车辆的运输载荷分别在模型中设置每辆车的最大运送容量。应急需求点数为10 个,各需求点对物资类型1、物资类型2和人员的需求数量进行正确报送后开始对算例进行计算。
3.2 算法性能对比
将文中算法与传统ACO 算法进行对比,算法的收敛过程如图2 所示。由图2 可知,在医疗资源应急优化调度仿真中,ACO 算法和所提AACO 算法的目标函数值分别在迭代次数为11 与32 后逐渐趋于稳定,但AACO 算法的最终收敛值为0.99,而ACO 算法为1.04。由此可见,文中算法在收敛速度、计算精度方面相比传统ACO 算法均有提升效果。
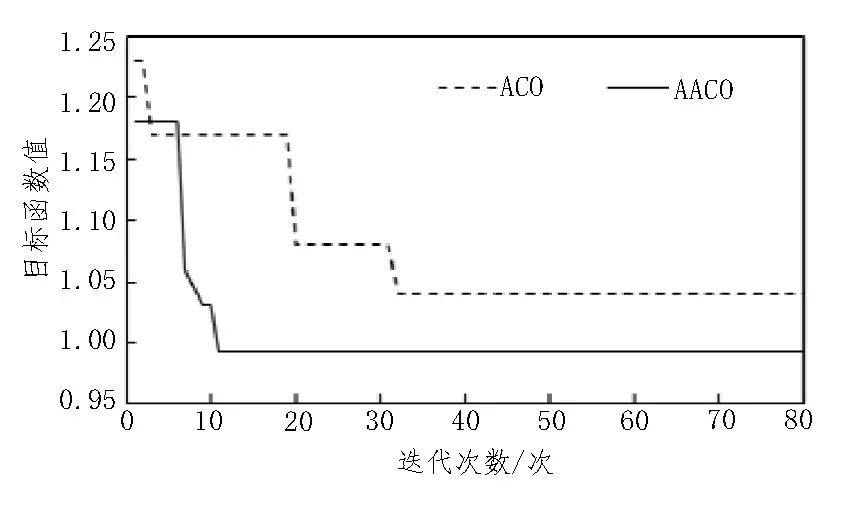
图2 算法迭代收敛过程
为确保优化调度结果的准确性,进行20 次计算,结果如表1 所示。由表1 可知,AACO 算法求得的最优值为0.992 3,最优目标函数值优于ACO 算法。从平均值而言,AACO 算法求得的平均值为1.022 4,优于ACO 算法的1.083 7。由此可见,文中算法在求解精度方面具备更优的性能。

表1 20次计算结果对比
3.3 不同优化目标对结果的影响
为研究不同优化目标对应急调度结果的影响,设置以下3 种场景进行对比。
场景1:文中所提应急优化调度模型,以应急需求点接收到医疗资源的满意度最大及医疗资源运送时间最短为综合目标;
场景2:仅以应急需求点接收到医疗资源的满意度最大为目标;
场景3:仅以医疗资源运送时间最短为目标。
3 种场景下的医疗资源应急优化调度结果如表2 所示。文中算法所得优化调度结果的总满意度为11.8,运送时间为26.9 h,相比于场景2,虽然总满意度降低了6.3%,但运送时间减少了26.3%;相比于场景3,虽然运送时间增加了8.5%,但总满意度提高了28.3%。由此可见,所提模型能够兼顾应急需求点对医疗资源的满意度与医疗资源的运送时间。

表2 不同场景的优化调度结果对比
4 结束语
在建立医疗资源应急优化调度模型的基础上,针对蚁群算法存在的缺陷,提出了改进策略,并将其应用于模型求解。所提AACO 算法的综合性能良好,且能够在提高应急需求点对医疗资源满意度的同时,减少运送时间。但是实际突发事件的复杂性和不确定性较强,因此如何考虑多种因素的影响,并建立随机性模型,进而实现医疗资源应急动态优化调度,将是下一步的研究重点。
