基于卡尔曼滤波和粒子滤波融合的UWB室内定位算法
2022-12-01程雪聪刘福才黄茹楠
程雪聪, 刘福才, 黄茹楠
(1.燕山大学 智能控制系统与智能装备教育部工程研究中心,河北 秦皇岛 066004;2.燕山大学 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
1 引 言
随着无线通信技术的发展,室内定位技术得到了广泛的应用[1~5],如仓储机器人的定位、机场中人员的定位等;然而在建筑物中,全球导航定位系统的卫星信号在穿透建筑的过程中快速衰减,导致其定位精度降低,甚至无法实现定位,而超宽带(ultra-wideband,UWB)定位技术凭借精度高、成本低成为了近年来被广泛应用的室内定位技术。
为了得到位置信息,通常使用到达时间差(time different of arrival,TDOA)的方法,该方法降低了室内定位系统对于系统时钟的要求,同时提高了定位精度[6,7]。基于协同定位的改进算法,是将双边两路测距(double-sided two-way ranging,DS-TWR)和TDOA结合,基于最小二乘和Taylor级数展开进一步实现室内条件下的精准定位[8~11]。在LOS(line-of-sight)环境中UWB的定位精度可以达到厘米级别;但在某些特殊环境下,例如仓储机器人所在的仓库,UWB信号会被人、货物或其他障碍物阻挡,因此产生NLOS (non-line-of-sight)误差,最终会导致UWB的定位精度下降[12]。在室内传统定位算法基础上,利用小波去噪消除NLOS误差,从而改进到达时间差定位算法[12~14]。利用卡尔曼滤波算法分别对UWB系统的测距信息和定位结果进行滤波处理,有效减小了测距误差,提高了定位的准确性[15]。
基于卡尔曼滤波的UWB室内三维实时动态定位算法,提出了一种不同观测条件下的自适应动态定位方法[16],进一步提高了定位精度。采用互补卡尔曼滤波对UWB和惯性测量单元(inertial measurement unit,IMU)进行数据融合的定位方法,该算法减小了IMU和UWB的数据噪声,从而提高了定位精度[17]。通过粒子滤波的方式融合IMU和UWB的数据,避免了定位轨迹突变现象的出现,并且提高了最终的平均定位精度[18]。采用基于2次粒子滤波的定位算法可以有效抑制NLOS误差的影响[19]。扩展卡尔曼滤波和粒子滤波融合的定位算法,在NLOS环境中可以减小错误数据对定位结果的影响[20]。实验结果表明,约束鲁棒迭代扩展卡尔曼滤波算法在NLOS环境中平均定位精度可以达到0.21 m左右[21]。采用机器学习技术来区分在LOS环境下和在NLOS环境下的UWB测量值,可以有效提高定位精度[22]。
本文使用3基站和1标签的UWB定位系统,提出卡尔曼滤波(Kalman filters and particle filters,KPF)和粒子滤波融合的算法,分别给出了在LOS环境下和在NLOS环境下基于KPF融合的定位算法,并与传统卡尔曼滤波、传统粒子滤波进行了比较。
2 UWB测距数据分析
为了分析LOS和NLOS环境下的UWB原始数据,在铺有0.5 m×0.5 m的瓷砖上进行了相关实验,可以明确实验中真实的运动轨迹。在实验过程中,通过遮挡标签T的天线来模拟NLOS环境。UWB定位系统中基站和标签中使用的核心芯片为DecaWave的DW1000芯片。
2.1 LOS环境下的UWB数据误差分析
如图1所示,记录了标签T与基站Ai之间的距离,i=0,1,2,并在表1中记录相关误差,实验结果表明,在静态的LOS环境中,UWB定位系统的测距能力较为稳定,测距误差均保持在厘米级。

图1 LOS环境下的测距结果Fig.1 Ranging results in LOS environment
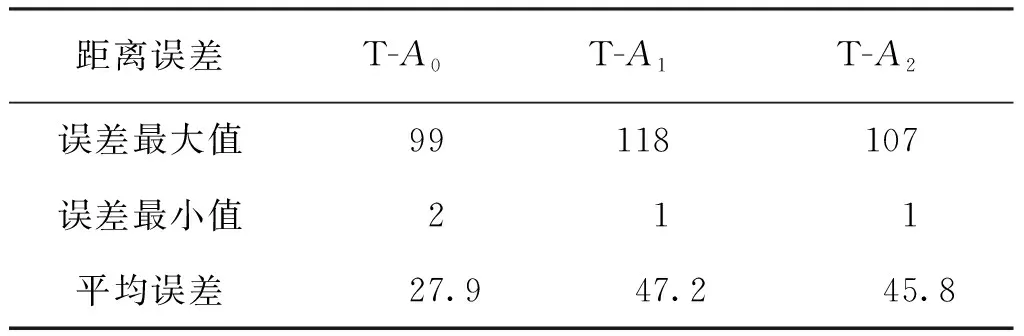
表1 LOS环境下基站与标签的距离误差Tab.1 Distance error between base station and tag in LOS environment mm
2.2 NLOS环境下的UWB数据误差分析
如图2所示,在保持标签T不动的情况下,通过遮挡标签T的天线会使UWB的测距信息产生较大误差,如表2所示,在NLOS环境下产生的误差最高可达692 mm,这将严重影响UWB的定位精度。
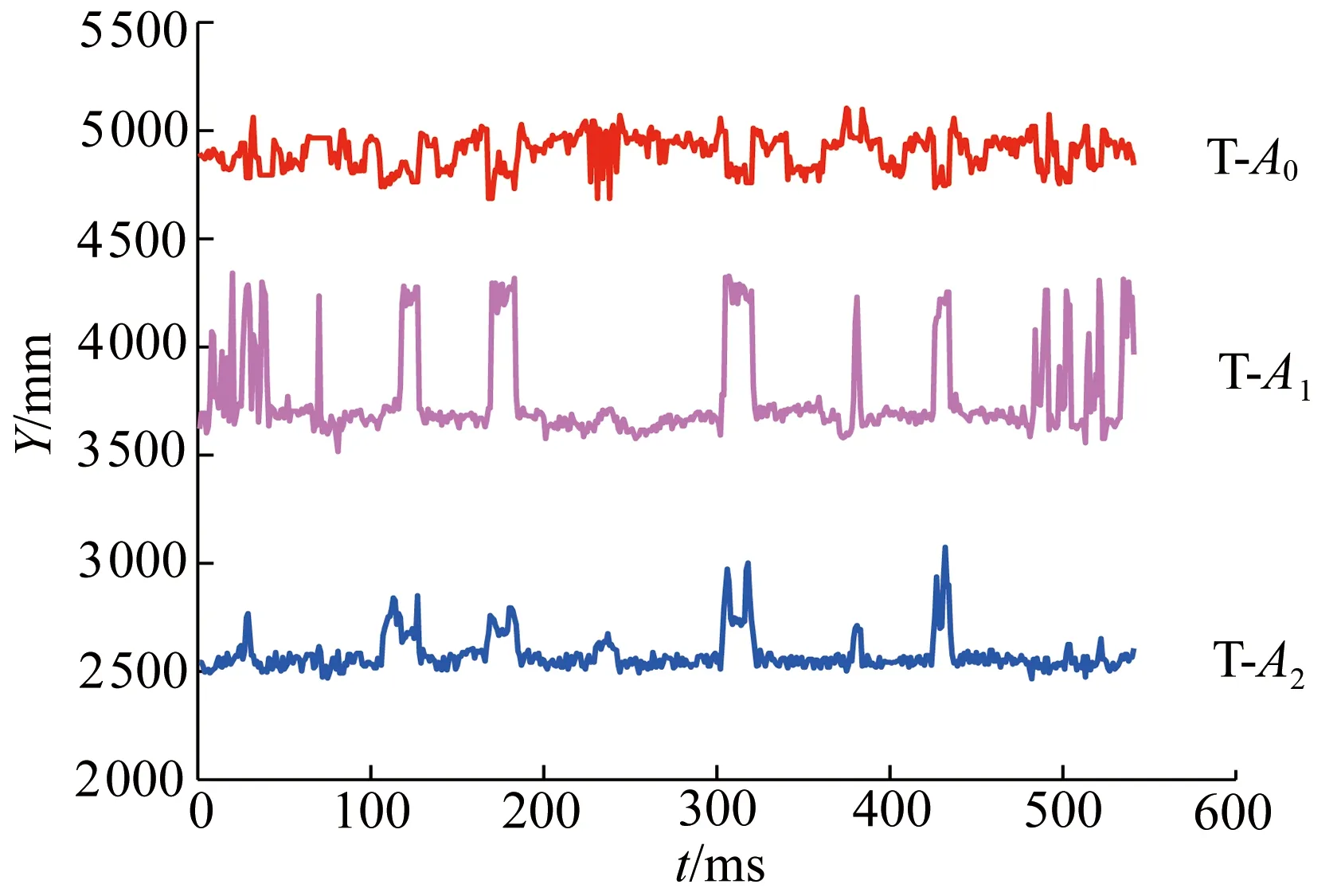
图2 NLOS环境下的测距结果Fig.2 Ranging results in NLOS environment
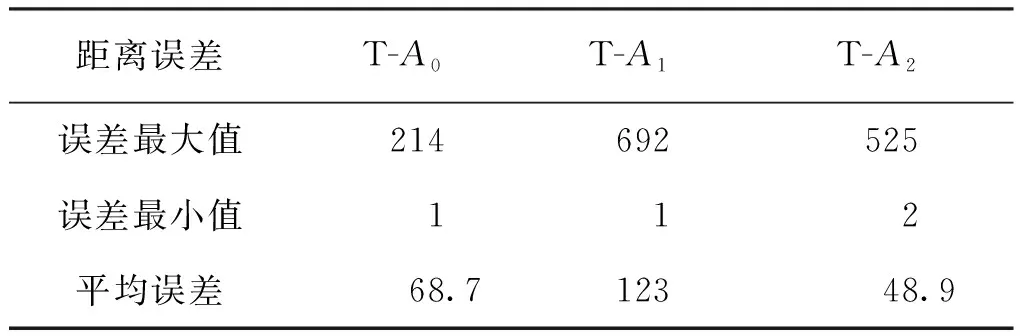
表2 NLOS环境下基站与标签的距离误差Tab.2 Distance error between base station and tag in NLOS environment mm
2.3 NLOS数据处理
对于在NLOS环境中获取的数据,本文采用改进卡尔曼滤波(improved Kalman filters,IKF)算法来消除NLOS误差。如图3所示,经过过滤的UWB数据变得相对更加平滑。

图3 NLOS环境下的测距滤波结果Fig.3 Ranging filtering results in NLOS environment
具体算法为:系统的状态方程和观测方程分别为式(1)和式(2),与传统卡尔曼滤波(Kalman filters,KF)相比,该算法求出了观测值与预测值的差en,并设定一个阈值h,通过比较|en|和h的大小来确定状态更新的值。
xn=Fnxn-1+vn
(1)
zn=Cnxn+wn
(2)
Step1:预测
状态预测:
xn|n-1=Fn|n-1xn-1+Q
(3)
误差协方差预测:
Pn|n-1=Fn|n-1Pn-1Fn|n-1+Q
(4)
观测值与预测值的差:
en=zn-Cxn|n-1
(5)
Step2:更新
卡尔曼增益:
An=CnPn|n-1CT+R
(6)
(7)
误差协方差更新:
Pn=(I-KnC)Pn|n-1
(8)
状态更新:
xn=xn|n-1+Knen
(9)
式中:vn为满足均值为0,协方差矩阵为Q的过程噪声;wn为满足均值为0,协方差矩阵为R的观测噪声;P为误差协方差;K为卡尔曼增益。
3 卡尔曼滤波和粒子滤波融合算法
现有的滤波处理算法有卡尔曼滤波、扩展卡尔曼滤波、粒子滤波等,这些算法在状态空间模型下给出了未知参数估计的有效解决方案。其中粒子滤波适用于非线性、非高斯分布,而且应用灵活、易于实施;其主要思想是通过蒙特卡洛采样模拟的方法,首先应用序贯重要性采样算法寻找一组在状态空间传播的随机样本近似地表示概率密度函数,然后用样本的均值代替积分运算,随着观测值的更新,不断调整粒子的权重和位置,并修正更新先验分布,最后得到目标函数的后验概率分布。该算法主要包括初始化、重要性采样、重采样3步。具体算法为:
Step1:初始化

Step2:重要性采样
对于i=1,2,…,N,采用高斯概率密度函数计算粒子的权值并归一化权值:
(10)
(11)

Step3:重采样
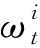
(12)

(13)
传统粒子滤波仅采用运动学模型而不利用观测信息进行随机采样,只有在定义粒子权重时才会用到观测信息,所以标准粒子滤波的粒子精度低,易出现粒子退化的现象。
基于上述分析,在重要性采样的过程中,应使采样的粒子尽可能地满足真实状态的概率分布,以提高粒子滤波的性能。基于此,本文提出了基于KPF的融合的算法,其基本思想和流程如图4所示。该算法通过卡尔曼滤波进行状态估计和误差协方差的更新,通过估计的状态和误差协方差进行粒子采样,使采样粒子尽可能地与真实状态一致。

图4 KPF算法流程图Fig.4 KPF algorithm flow chart
4 实验分析
实验设计了2条路线,路线1为L型折线,路线2为矩形,每次实验分别在每条路线上走2个来回。算法的定位测试共设计了2种方案,一种是在LOS环境下,另一种是在NLOS环境下,通过计算定位误差来评估算法的性能和可靠性。
4.1 LOS环境下的定位路线分析
图5展示了基于各种算法的定位路径。基于UWB原始数据的定位结果用绿色路径表示,由于UWB数据中存在大量的噪声,基于该算法的路线1定位结果与实际路线的平均误差为32.9 mm,最大误差为147.7 mm,;路线2定位结果与实际路线的平均误差为30.5 mm,最大误差为175.9 mm。基于PF算法的定位结果中用黄色路径表示,该算法可以根据UWB数据来校正当前的定位结果,使用该算法,路线1和路线2的平均误差分别为31.5 mm和29.4 mm。基于KPF的融合定位算法的定位结果用蓝色路径表示,可以在实验中看到,该算法在路线1中的平均误差为22.1 mm,在路线2中的平均误差为25.8 mm,相对于使用UWB原始数据进行定位,定位精度平均提高了20.6%。

图5 LOS环境下各算法定位路径Fig.5 Algorithm positioning path under LOS environment
4.2 NLOS环境下的定位路线分析
图6显示了受到NLOS环境干扰时基站与标签之间的距离数据,在图中可以明显看到,当定位基站和定位标签处于NLOS环境中则数据会产生NLOS误差,此时UWB定位系统中得到的距离数据会产生突变,进而导致定位产生偏差。如图6所示,含有NLOS误差的距离数据在通过IKF滤波后,基本可以去除NLOS环境导致的误差,使距离数据更加平滑、稳定。

图6 NLOS环境下2条路线滤波后的UWB测距信息Fig.6 Filtered UWB ranging information of two routesin NLOS environment
图7展示了在NLOS环境下基于各种算法的定位路径,其中绿色表示UWB数据的定位路径,虽然经过IKF滤波已经消除了大部分NLOS误差,但最大定位误差依然达到了196.2 mm;黄色表示经过PF滤波的定位路径,该算法可以适当矫正误差,但矫正能力十分有限,平均定位误差为34.9 mm;KPF算法的定位路径用蓝色表示,该算法可以充分利用KF中的状态更新量和误差协方差,该方法的定位结果相对较平滑,平均误差为31.1 mm。

图7 NLOS环境下2条路线各算法定位路径Fig.7 Positioning paths of each algorithm in two routesunder NLOS environment
5 结 论
本文提出了一种卡尔曼滤波和粒子滤波融合的定位算法,该算法通过KF更新的状态和误差协方差进行粒子采样,克服了传统粒子滤波采样粒子和真实状态不相符的缺点,大幅减少了粒子退化的现象,充分提高了UWB定位系统的定位精度。由实验可以看出该算法在LOS环境和NLOS环境下均有较好的定位精度。后续将针对更复杂的应用需求,继续研究基于IMU/UWB的定位系统,通过多传感器的数据融合进一步提高定位系统的精度和鲁棒性。
