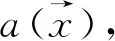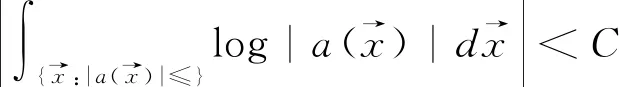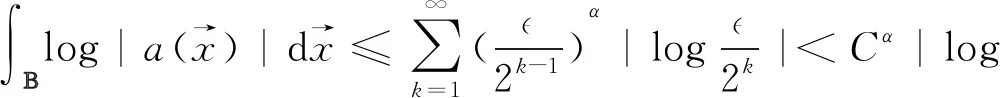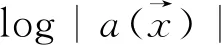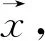高维解析Jacobi算子的Lyapunov指数的log-Hölder连续性
2022-12-01尤安迪陶凯
尤安迪,陶凯
(河海大学理学院,江苏 南京 210098)
0 引言
在本文中,我们将研究定义在l2()上的如下拟周期解析Jacobi算子
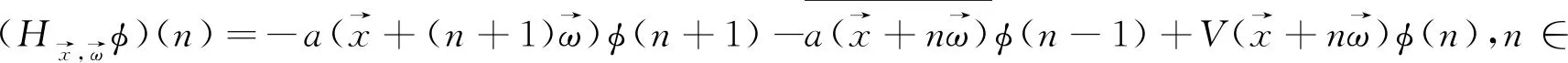
(1)
其中V:d→是一个实解析函数,a:d→是一个复解析函数且不恒为d被称为初相,被称为频率.
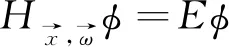
因此,我们定义
(2)
则
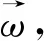
是一个Jacobi斜积流.
显然,如果我们定义
为系统的n步转移矩阵,则
在本文中,我们主要考虑系列的Lyapunov指数的连续性问题. 首先,我们定义有限Lyapunov指数
显然,它们是满足次可加性的,即对任意大于零的正整数m,n,都有
nLn+mLm≥(m+n)Lm+n.
(3)
此即为本系统的Lyapunov指数.
(4)
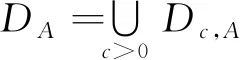
至此,我们介绍本文中的主要结论:
f(x,y)=sin2πx-sin2πy.
离散哈密顿算子的Lyapunov指数的连续性问题一直是本领域内的热点问题.在文献[1]中,Goldstein-Schlag研究了定义在一维环面上的解析离散薛定谔方程
(Sx,ωφ)(n)=φ(n+1)+φ(n-1)+v(x+nω)φ(n),n∈
(5)
他们开创性地使用了大偏差定理和雪崩原理(具体定义见下一节)来研究这一问题,证明了当势能v是一维解析函数且频率ω为强Diophantine数时,算子的Lyapunov指数关于能量E是Hölder连续的.此后,包括菲尔兹奖得主J.Bourgain,A.Avila等人,都利用这一套工具研究相关算子的Lyapunov 指数各类问题,如文献[2-4].另一方面, 尤建功与王奕倩等人在文献[5-6]中也给出了Lyapunov指数不连续的例子.最近, 韩瑞和张世文在文献[7]中研究了薛定谔算子(5)在任意无理数频率下的Hölder连续性问题,而陶凯在文献[8]中将这一结果推广到了本文中所研究的更一般的Jacobi 算子(1)上.
与本论文直接相关的是文献[9-10]. 在文献[9]中,陶凯研究了定义在一维环面上的解析Jacobi算子(1)式的同类问题.而在文献[10] 中,陶凯研究了高维解析斜积流所对应的Lyapunov 指数的连续性问题,即
(6)
1 准备工作
在本节,我们主要进行主定理证明的准备工作.
首先,需要说明的是,对于Lyapunov指数的连续性问题,我们只要考虑算子谱集上的能量E即可.这是因为,在预解集上,其是一个C∞函数.注意到,此算子的谱必然在如下的闭区间中:
(7)
所以在本文中,我们只需要考虑E∈ε上的证明即可.
其次,在上一节,我们说过,Goldstein-Schlag[1]创造性地给出了一套证明Lyapunov指数连续性的方法,此后,包括上述所提到的所有文献在内,大家都在使用此方法进行研究.经过约20年的发展,学者们发现,只要得到了所研究的动力系统所对应的大偏差定理,则使用如下的雪崩原理,可以非常顺利地得到最后的Lyapunov指数的连续性.
命题3(雪崩原理) 令A1,…,An为2×2矩阵的序列,其行列式满足
(8)
假设
(9)
且
(10)
那么
(11)
其中C为某个绝对常数.
同样地,在本文中,我们只要得到如下被称为大偏差的定理,则剩下的内容可以直接使用文献[10]中的第三部分即可:
故本文中只需要证明定理4. 为此,我们主要需要关于高维次调和函数的强Birkho遍历定理.如果T是可测空间(X,Σ,m)上的一个遍历映射,函数f是X上的m-可积函数,则对几乎处处x∈X,其“时间平均收敛到“空间平均”.但此定理并没有告诉我们上述的收敛速度.因此,我们将给出这一速度的定理称为强Birkho遍历定理.
再次, 我们来介绍次调和函数.先介绍一维的情况.设u(z)是定义在复区域Ω⊂上的实值函数.
定义5[10]我们称u(z)是定义在区域Ω上的次调和函数,如果
1)u(z):Ω→[-∞,+∞);
2)u(z)是从Ω映入[-∞,+∞)上半连续函数;
3)对任意的z1∈Ω, 总存在r1=r1(z1)>0使得对任意的0 (12) 此时, 我们可以用递归的方法定义高维次调和函数: 注7当f(z)是解析函数时,由Jensen公式: 因此,在文献[10]中,函数 也是次调和的. 所以,为了得到其对应的大偏差定理,证明了如下的对于uN的强Birkho遍历定理: (13) (14) 至此,我们完成了所有的理论背景的介绍.我们将在下一节中给出大偏差定理,即定理4的证明,从而得到本文关于连续性的主要结果. 首先,我们需要注意的是,本文中考虑的斜积流(2)是亚纯的,而非解析的.因此,为了使用命题8,我们需要对其解析化.具体地,我们定义 和 (15) (16) (17) 定义 (18) 由(15)式可得 (19) 其中 (20) 这里, 为了让系统有意义, 我们需要说明常数D是有限的. 引理9的证明我们证明一个更强的结果:对任意>0, 由(14),我们得到 (21) 因此, 引理10对任意的正整数k,都有 (22) 并在命题8中取N=1,注意到此时 则由命题8直接得到本引理. 此时,由于(15),(16),(19)式以及引理10,我们会发现, 想要证明大偏差定理4, 其实只要证明 即可. (23) 引理11的证明注意到 故 类似地, 故 进一步地, 我们有 性质12(1) (2) 性质12的证明(1)由引理11和三角不等式直接得到. (2)对任意的1≤k≤K, 由于 和 则 同样地, (24) 因此, 取δ=k1-τ1,并使用引理10,可得 (25) 注意到,我们此前已经取定k=N1-2σ且已经证明D是一个有限常数,故|(k+1)D+k1-τ1|≤N1-σ,从而有 (26)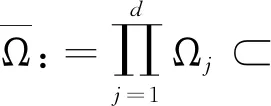
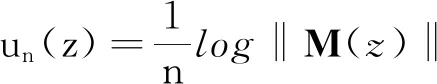
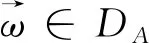
2 大偏差定理的证明