合理设计探究问题，用数学的方式育人——以苏科版数学七（上）“数轴”习题课教学为例

■余叶军 杨广清

大部分教师往往采用有序评讲的方式进行习题课的教学，这种方式缺少知识的重新架构、宏观的视角、整体的思维，与当下大单元教学的观念背道而驰。要想切实地解决这些问题，习题课教学就要在知识的整体结构、核心内容和重要思想上做文章，让学生既见树木也见森林；要以知识为载体，思想方法为核心，提高解决问题的能力为切入点，最大限度地让学生在课堂学习中承担主人翁角色，有效体现思维的生长性、深刻性、灵活性、创造性，从而落实立德树人的根本任务，彰显数学学科育人的价值。

一、教学背景

本节课是一节“乡村共同体”联合示范课，教学对象为一所学校的七年级学生。本节示范课教学目标是学生通过对数轴的再认识，感受数形结合的思想，建立方程的模型，提升数学思考能力，为后续平面直角坐标系的学习作铺垫。由此明确了本节课的教学理念是在活动中生成，在生成中成长。本节课的教学主线是让学生说一说、画一画、算一算，进而发现问题、提出问题、分析问题、解决问题、归纳总结方法，最后进行相关知识的应用。

二、教学过程

师：同学们，我们已经学习了数轴的相关知识，请你说说你心中的数轴是什么样子的。

生1：一条有正方向的直线。

生2：还有原点和单位长度。

师：请你画一条数轴，说说数轴可以帮助我们解决什么问题。

生3：正数、0、负数可以在数轴上有序排列。

生4：可以利用数轴比较数的大小。

设计意图：学生通过想一想数轴的样子，在脑海中直观感受数轴的形象；再通过画一画让这种感受成为现实，也提高了作图的能力；最后，通过说一说，进一步体现理性思维。

活动探究1读图（图1）获取信息：

图1

师：我们能从图1中得到哪些信息？

生5：我能得出A、B、C、D四个点表示的数分别是-3、-1、2、3。

生6：这四个数的大小关系从图中能直接看出。

生7：能求出每个数的绝对值。

师：绝对值的定义是什么？

生8：绝对值表示数轴上的点到原点的距离。

师：那么数轴上点A到点B的距离是多少？

生9：点A到点B的距离是2。

师：你是怎么得出的？

生9：我是从图中直接看出来的。

师：非常棒！借助数轴，直接看出，几何直观，一目了然。请同学们看图2，此时数轴上点A和点B的距离是多少？还能直接看出来吗？

图2

学生一脸茫然，随后陷入沉思，小组交流，教师巡视。

师：有想法了吗？

生10：AB=b-a。

师：把你的想法和同学们分享一下。

生10：我是借助于图1，多举几个特殊的例子，然后由特殊到一般，归纳出一般性的结论。

师：我发现了有部分同学的结果是a-b，正确吗？

生11：正确，因为a-b是负数了，距离不能为负数。

师：距离可以用之前学的什么知识来表达？

生12：绝对值。我们可以求a-b的绝对值。

师：那么，我们可不可以把结论的形式统一呢？

生13：AB=|a-b|或 |b-a|。

设计意图：看图说话是学生将图形语言转化为符号语言的重要途径。这一环节设计了一个开放性的获取图形信息的问题，既是对学生数轴知识的再一次唤醒，又是对学生思维能力的再一次提升。教师让学生用代数式表示线段长，展现不一样的思考方式，最后通过一个一致性的表达去统一思想，体现了数学结论之美。在渗透数形结合思想的同时，也为后续解决问题提供了生长点。

活动探究2观察图3，回答下列问题：

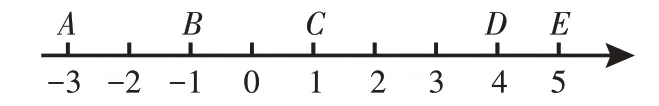
图3

（1）| 4-1|表示哪两个点之间的距离？|4-（-1）|呢？

（2）你会用式子表示A、C两点之间的距离吗？

（3）数轴上点A表示的数是-3，另有一点P表示的数是x，你会用式子表示A、P两点之间的距离吗？

（4）你能说说 |x+1|表示的含义吗？

（5）若x表示一个有理数，你能说说 |x-1|+|x+3|表示的含义吗？观察数轴，你还有什么想法？

师：同学们对哪一个问题疑惑最大？

生14：我们小组对问题（5）疑惑最大。

师：其他小组是否也有同样的疑惑？举手示意。

师：问题（5）与问题（4）有联系吗？我们的经验在哪里？可以怎样变形呢？

生15：式子|x-1|+|x+3|可以变化为|x-1|+|x-（-3）|。

师：很好，离成功不远了，这样我们就可以用数学的语言来表达这个式子的含义了。

生16：从数轴上看，我们可以理解为x到1和x到-3之间的距离和。

师：表达得非常准确。我们再用变化的眼光去直观感受一下，在x变化的过程中，x到1和x到-3之间的距离和怎么变化呢？

生17：利用数轴，我发现x在1和-3之间时距离和最小，最小值为4。所以|x-1|+|x+3|最小值为4，没有最大值。

师：问题（5）从数的角度很难解决，因为涉及七（下）的一元一次不等式和分类讨论的数学思想，难度较大。因此，我们可以根据式子的特征联想到数轴，通过几何直观，利用数形结合来解决。

设计意图：活动探究2以问题串的形式给学生搭建思维的“脚手架”，让不同层次的学生都能体会到成功的喜悦，实现自我价值。教师以问题串的形式，让探究走向纵深，体现了深度教学，促进学生深度学习，培养学生高阶思维，让学生在已有数学活动经验的基础上，积极思考，主动利用类比去探究、去构建，激发数学思维活力。

活动探究3观察图4，获取信息：

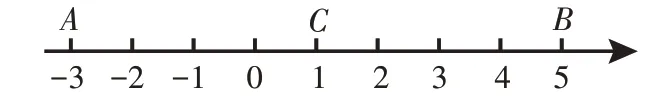
图4

师：AC+BC等于多少？

生18：AC+BC=8。

师：若点P在线段AB上，则PA+PB等于多少？

生19：PA+PB等于8。

师：若点P在数轴上，且PA+PB=10，你能求出点P表示的数吗？

生20：PA+PB=10时，点P有两个位置。若点P在点A的左侧，则点P表示的数是-4；若点P在点B的右侧，则点P表示的数是6。

生21：借助前面的学习经验，我可以设点P在数轴上表示的数是x，因为PA+PB=10，可以得出 |x-（-3）|+|x-5|=10，然后分类讨论求解。

师：两位同学经过思考都形成了自己的解题方法，成功利用本节课的知识解决了问题。同学们能否根据图4，在刚才的基础上再提出一个问题呢？

生22：若点P在数轴上，求PA+PB的最小值。

生23：若点P在数轴上表示的数是x，当PA+PB有最小值时，这个x的位置确定吗？

生24：若点P在数轴上，PA+PB+PC有没有最值？

师：同学们的问题都非常具有创新性和挑战性。请同学们利用课后时间相互交流，解决问题。

设计意图：通过活动探究3的学习，学生感受到由特殊到一般、数形结合、分类讨论的思想，进一步体会知识间的联系，建立方程的模型。教师让学生利用自己的学习经验提出问题，培养了学生的质疑精神，让学生自己分析问题，解决问题，带着问题走向课后，实现由课堂走向课后的教学评价体系，让评价体系更加完整。

三、教学反思

1.合理设计探究问题，促进学生整体领悟

“双减”背景下，如何让学生在课堂学习中获得更多，在课后自我发展，构建生长型习题课就尤为重要。生长型习题课需要学生对所学的知识有着很好的整体领悟能力，而合理设计探究问题是促进学生整体领悟的一个有效路径。如活动探究1，教师通过一系列的问题串，不断地让学生去回忆数轴的定义、用途，为后续深度探究奠定了坚实的知识基础。学生通过自己的合理探究，得出了数轴上任意两点之间的距离表达式，归纳出后续应用的结论。在有序的思考中，学生经历问题解决的完整思维生长过程，从而达到数学思维经验化、能力化、成长化。

2.合理设计探究问题，促进学生深度思考

促进学生深度思考要以学生的实际能力为出发点，设计能引领学生思考、有梯度、有价值的问题，让问题成为思维提升的有效着力点。如活动探究2，以问题串的形式呈现，问题设计层层递进，探究难度逐步增加，思维要求逐步提升，能力要求逐步提高，一系列的问题全方位地锻炼了学生的数学思维。探究问题时，不仅要求学生会用数学的眼光去观察，会用数学的思维去思考，更要会用数学的语言去表达。比如“你能说说 ||x+1表示的含义吗？”这就需要学生有联系地去学，整体地去想，在活动中去深度探究，在深度学习中体会数学内部是相互联系的。

3.合理设计探究问题，促进学生质疑评价

学生的质疑是课堂教学宝贵的财富。对于同一个问题，不同的学生往往会用不同的方法去思考，这就需要教师合理设计探究问题，引导学生去提炼、概括，寻找普适性的方法，然后举一反三，产生迁移。在迁移过程中，教师引导学生对这种方法进行再加工，从中提炼出可以适用于一般的、具有广泛应用性的数学思想方法。如活动探究3，在前两个活动探究的基础上，教师引导学生自主提出问题——“若点P在数轴上，求PA+PB的最小值。”“若点P在数轴上表示的数是x，当PA+PB有最小值时，这个x的位置确定吗？”这样的质疑不是一开始就具备的，而是在本节课一个个活动层层探究后产生的，充分说明本节课前面两个活动探究的学习是有价值的，体现了合理设计探究问题的必要性。学生能够有效地从数量特征联想到几何特征，从而把数的问题转化为形的问题，创造性地利用形来解决数的问题。在此过程中，学生感受到了成功的喜悦，培养了创新才能，激发创新意识，也进一步体现了数学育人的方式。