ECC 单轴受拉损伤本构模型研究
2022-11-30赵大鹏刘伟康范家俊
李 可,赵大鹏,刘伟康,范家俊
(1. 郑州大学土木工程学院,河南,郑州 450001;2. 哈尔滨工业大学土木工程学院,黑龙江, 哈尔滨 150006)
ECC 是20 世纪90 年代提出并不断发展的一种新型水泥基复合材料[1]。由于纤维的存在,ECC在受压、受拉和弯曲作用下表现出超高的韧性[2]、能量耗散[3]以及抑制开裂效应[4]。因此,ECC 被广泛应用在各类受损结构的修复和加固工程[5−9]。
ECC 受拉本构模型是ECC 被研究和应用的前提。常用的ECC 受拉本构模型有:不包含软化段的三折线模型[10]和双折线模型[11],包含软化段的三折线模型[12−14]。但这些模型忽略了应力-应变关系的非线性特征,也不能描述拉力作用下微观缺陷的发展所造成的ECC 损伤状态。损伤本构模型是利用损伤力学方法来描述材料应力-应变关系的新方法,并成功地应用在混凝土等材料[15−17]。因此,一些学者开始利用损伤力学方法研究应变硬化水泥基材料的本构模型。
KABIR 等[13]利用应力法定义了ECC 的拉压损伤因子,基于ECC 的损伤模型,使用有限元方法研究了预制ECC 和轻质混凝土组合钢梁的弯曲和粘结性能。KRAHL 等[18]对超高性能纤维增强混凝土(UHPFRC)的拉压损伤演化规律进行了单调和循环荷载试验和数值模拟研究,并利用刚度法定义了UHPFRC 的损伤因子,然后,基于试验数据得到损伤因子的具体表达式。HE 等[19]同样利用刚度法定义了应变硬化水泥基复合材料(SHCC)的损伤因子,并分析了SHCC 在单轴受力状态下的损伤演化规律。之后,CAI 等[20]利用刚度法定义的ECC 损伤因子分析了ECC 钢管混凝土组合柱的抗震性能。CHEN 等[21]和HU 等[22]分别在对高层建筑和FIU 桥梁进行数值模拟研究时,采用Najar 能量方法定义了混凝土的损伤因子,CHENG等[23]也利用该方法定义了ECC 的拉压损伤因子。
然而,应力法定义的损伤因子只能表达应力达到峰值应力之后的损伤,ECC 在首次开裂后的应变硬化阶段的损伤则不能体现。刚度法和能量法定义的ECC 损伤因子能够表达ECC 受力全过程的损伤,但是这两种方法预测的损伤演化曲线不能反映应ECC 受拉应变硬化和应变软化两个阶段不同的损伤机制。
因此,本文致力于针对能够合理描述ECC 单轴受拉各阶段损伤机制的非线性本损伤构模型的研究,进行以下研究工作:首先,对ECC 试件进行单轴单调拉伸试验,分析了不同PVA 体积掺入量和水胶比对受拉力学性能的影响规律,揭示在单轴拉伸作用下ECC 的损伤演化规律;进而,基于ECC 受拉损伤演化规律,提出ECC 单轴受拉损伤本构模型和模型参数的计算方法;最后,将模型计算应力-应变关系结果和试验结果作对比,以验证本文模型的精确性和合理性。
1 试验研究
1.1 试件设计
本文制作ECC 采用的原材料有自来水、普通硅酸盐水泥(P.O.42.5)、PVA 纤维、粉煤灰(一级)、微硅粉、细砂(最大粒径不大于74 µm)以及聚羧酸高效减水剂。通过单轴拉伸试验,探究PVA 纤维体积掺量(v)和水胶比(r)两种因素对试件拉伸性能和损伤演化的影响规律。试验中共设计5 组试件,每组5 个试件,试件尺寸为厚度×宽度×长度=13 mm×40 mm×280 mm。试验在电液压伺服材试验机上进行,加载速度为0.2 mm/min。加载装置及试件尺寸如图1 所示。试验ECC 配合比见表1 所示。

图1 加载装置与试件尺寸 /mmFig. 1 Test setup and specimen size

表1 ECC 配合比 /kgTable 1 ECC mix proportion
1.2 ECC 拉伸试验结果
根据ECC 单轴受拉试验,各组试件的受拉力学性能指标实测值(开裂应变εk、开裂应力σk、峰值应变εp、峰值应力σp和极限应变εu)如表2所示。
应当指出,表2 中的数据为各组的平均值,其中C 组和E 组由于试件结果偏差较大而剔除了2 个试件的数据,每组的平均变异系数(每项力学指标变异系数的平均值,并以此来衡量该组试验数据的离散程度)分别为:A 组为0.214,B 组为0.238, C 组 为 0.171, D 组 为 0.212, E 组 为0.098。因此,从表2 可以看出,当ECC 试件水胶比为0.28 时,A、B 和E 组试件的PVA 纤维体积掺入量从0.01 增加至0.015 和0.02 时,开裂应变分别增加25%和125%,开裂应力分别增加2.1%和6.4%,峰值应力增加19.36%和19.76%,峰值应力点对应的峰值应变分别增加25.5%和300%,试件断裂时的极限应变分别增加26.8%和99.5%。当ECC 试件的PVA 纤维体积掺入量为0.02 时,C、D 和E 组试件的水胶比从0.24 增加至0.25 和0.28 时,开裂应变分别增加75%和125%,开裂应力分别降低15.7%和41.6%,峰值应力降低13.6%和35%,峰值应变分别增加64%和340%,极限应变分别增加25.1%和77.1%。以上分析表明,PVA 纤维体积掺入量的增加能够显著增加ECC 的变形能力,但对强度影响不明显;水胶比的提高能够提高ECC 的变形能力,但会降低ECC 的强度。
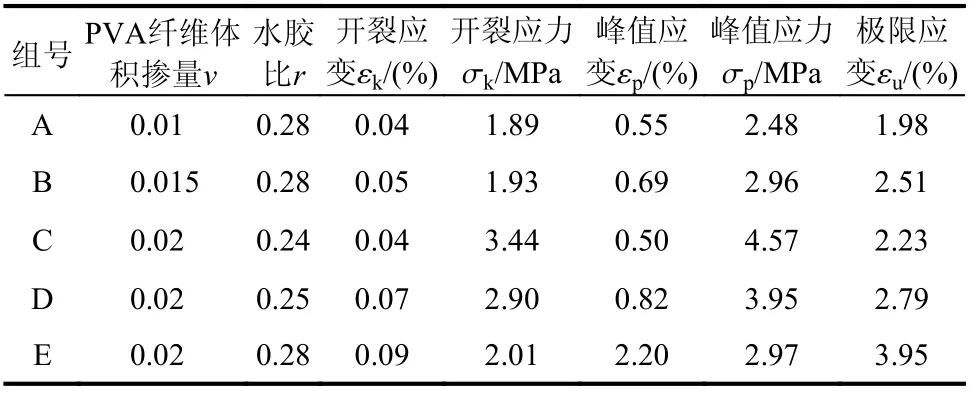
表2 试验结果Table 2 Test results
典型试件的受拉应力-应变全曲线如图2 所示。ECC 在受拉过程中表现出明显的应变硬化现象,随着PVA 纤维体积掺入量的和水胶比的增加,应变硬化段明显延长;当应变达到峰值应变后,进入应变软化阶段,直至达到极限应变发生断裂。

图2 典型拉伸应力-应变曲线Fig. 2 Typical tensile stress-strain curve
1.3 ECC 受拉损伤演化机制分析
试件典型破坏过程和损伤演化过程如图3 所示,根据ECC 受拉应力-应变曲线的形状和受力特点,可将ECC 单轴拉伸损伤演化分为以下3 个阶段进行描述:

图3 应力-应变曲线特征与损伤演化机制Fig. 3 Stress-strain characteristics and damage evolution mechanism
第一阶段:弹性无损阶段,此阶段为试件开始加载到首次开裂的直线段, ECC 受拉应力与应变在此阶段近似线弹性关系,ECC 基本处于无损状态。
第二阶段:应变硬化与稳定损伤阶段,此阶段为从首次开裂点到峰值点之间的曲线段。这一阶段试件的应力随着应变的增加而缓慢增加,裂缝数量也不断地增加,表现出明显的应变硬化和多缝开裂现象。试件的损伤开始在开裂截面处开展,但是由于PVA 纤维的桥联作用,试件表面不断有新的截面产生新的水平细长裂缝。这说明损伤被分散和转移到其他的截面位置,直到应力达到峰值应力,试件表面不再产生新的裂缝。
第三阶段:应变软化与不稳定损伤阶段,此阶段为峰值点之后的下降段。在该阶段,随着应变的增加,应力开始下降,纤维开始不断的从基体中被拔出或被拉断,试件表面的细小裂缝随着应力的下降开始逐渐变宽。由于基体中纤维的失效,损伤快速增加,使得损伤处于不稳定的增加状态。最终,试件标段内的某处形成主裂缝,试件最终在主裂缝处断裂。
2 模型研究
2.1 本文ECC 受拉损伤模型的建立
为更好反映不同阶段损伤发展特征,本文采用应力应变曲线上一点与原点之间割线与横轴夹角变化程度表达的ECC 受拉损伤因子(见图4(a)及式(1)),同时根据1.3 节所分析的损伤演化过程,将损伤演化曲线定义为分段函数曲线,如图4(b)所示。在弹性阶段,ECC 的损伤因子为零,反映了该阶段ECC 处于弹性无损伤状态;在应变硬化阶段,损伤因子随应变增长相对缓慢,且增长速率减小,可反映该阶段损伤稳定缓慢发展特性;在应变软化阶段,损伤因子随应变增长相对较快,且增长速率不断增加,可反映该阶段损伤失稳快速发展特性。
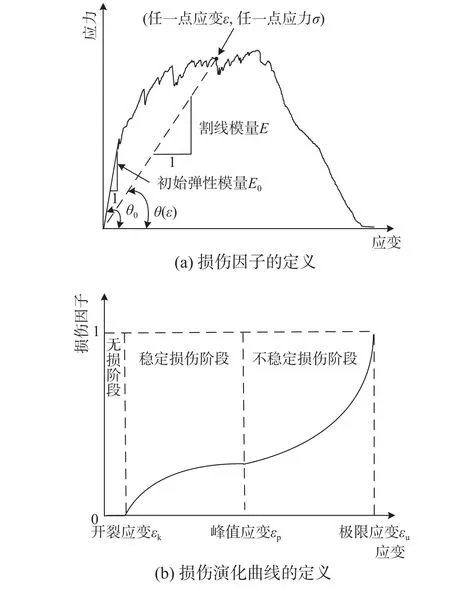
图4 本文损伤因子与损伤演化曲线的定义Fig. 4 Definition of damage variable and damage evolution curve in this paper
因此,损伤因子可表达为:

式中:θ0为ECC 试件单轴受拉弹性阶段的应力-应变曲线与横轴的夹角;θ 为ECC 试件单轴受拉应力-应变曲线的割线与横轴之间的夹角。

式中:E0为初始弹性模量;E为割线模量;ε 为ECC 试件单轴受拉应变;σ 为ECC 试件单轴受拉应力。
因此,应力-应变关系可以表达为:
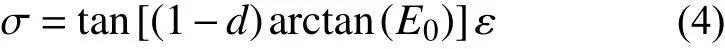
根据本文1.3 节对ECC 单轴受拉损伤演化机制的分析,可以假设损伤因子的函数为如下形式:
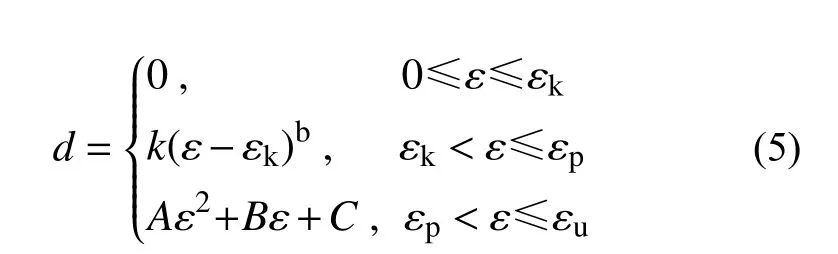
式中:k、b、A、B和C为模型系数。
同时,损伤因子表达式应满足如下边界条件:

2.2 模型系数求解与损伤演化分析
从上述模型系数表达式(9)~式(11)中可以看出,只有b和A两个系数为独立未知量。为确定这两个系数,可以通过对试验结果进行拟合分析的方法实现。采用式(5),对各组试件的损伤因子-应变曲线进行拟合,得到各组试件的模型系数b和A的值,然后将b和A代入式(9)~式(11),得到系数k、B和C的值,如表3 所示。
由表3 可知,系数b和A随PVA 纤维体积掺入量和水胶比的增加而减小,说明在应变硬化和应变软化阶段PVA 纤维体积掺入量和水胶比均对损伤演化产生影响。因此,系数b和A可以拟合为PVA 纤维体积掺入量和水胶比的函数,相关系数R2分别为0.974 和0.973,表达式为:

表3 损伤模型系数Table 3 damage model coefficients
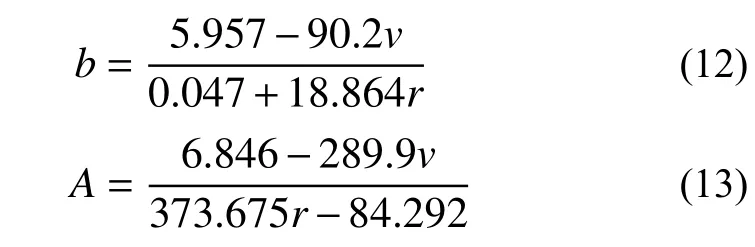
式中:PVA 纤维体积掺入量v的适用范围为0.01~0.02;ECC 水胶比r的适用范围为0.24~0.28。
损伤模型系数b和A的实际结果与PVA 纤维体积掺入量v以及ECC 水胶比r的关系如图5所示。

图5 损伤模型系数b 和A 与PVA 纤维体积掺入量v 和水胶比r 的关系Fig. 5 The relationship between damage parameters (b and A)and PVA fiber volume v and water-binder ratio r
基于上述模型系数的数值拟合分析,为了进一步分析应变硬化段和应变软化段损伤演化的规律,对该阶段损伤因子关于应变求一阶导数和二阶导数,如下式所示:
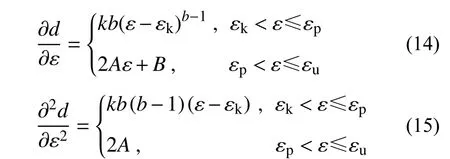
从式(14)和式(15)可以分析得出,在应变硬化阶段,损伤因子一阶导数(即损伤速率)大于0,但是二阶导数却小于0,这反映了ECC 在该阶段损伤发展特征,即损伤虽然不断累计增加,但由于纤维的存在使得损伤增加的速率不断降低,处于稳定发展状态。在应变软化阶段,损伤的一阶导数和二阶导数均大于0,这亦反映了ECC 在该阶段发展特点,即由于PVA 纤维的不断拔出或拉断破坏,导致ECC 损伤程度快速增长,且增长速率不断增大,处于不稳定损伤状态。以上的分析与1.3 节ECC 受拉损伤演化机制分析的一致,这也说明本文假设的损伤因子表达式(5)能够合理的反映ECC 受拉损伤演化规律。
2.3 模型验证
为验证所提模型的适用性,本文进行了验证试验。验证组试件的尺寸、制作、加载与试验组相同,共设计5 组,每组2 个试件。但由于试验加载等其他因素导致VC 组试验结果离散太大而舍弃,其余各组试验数据分别为各组的平均值。验证组的试验参数及试验结果如表4 所示。

表4 验证组试验结果与损伤模型系数Table 4 Test results and damage model coefficients of the verification groups
与试验组相同,仍以每组ECC 单轴拉伸试件力学性能指标的平均变异系数来衡量该组试验数据的离散程度。VA 组的平均变异系数为0.130,VB 组为0.181,VD 组为0.091,VE 组为0.099。
为了验证损伤模型系数b和A,现利用验证组实测值b0和A0(每组的平均值)与式(12)和式(13)计算值对比,对比结果如表5 所示。

表5 验证组损伤模型系数b、A 与计算值Table 5 Comparison of b and A of the verification group with the calculated values
由表5 可以看出,损伤模型系数b和A的实测值与计算值之比的均值分别为1.040 和1.049,其变异系数为0.021 和0.115,这说明利用式(12)和式(13)计算验证组的损伤模型系数b与A是合理的,进而可以对验证组的损伤演化曲线以及应力-应变曲线进行对比。
将表4 中的数据代入式(9)~式(13)和式(5),可以计算得到验证组试件的损伤演化曲线,并与验证组试件试验损伤演化曲线对比,如图6 所示。将试验组和验证组受拉基本参数代入到模型系数计算式(9)~式(11)计算出模型系数,然后将模型系数代入式(4)和式(5),可以得到模型预测的ECC 受拉应力-应变关系曲线。为了验证本文模型的准确性,现将试验数据、本文模型计算结果以及ECC 受拉三折线应力-应变曲线模型[12− 14, 24 − 25]三者相互对比,如图7 所示。
从图6 可以看出,验证组试件的损伤演化曲线在达到峰值应力前和本文模型预测结果十分接近,达到峰值应力后的不稳定损伤阶段实测结果和模型预测结果存在误差,但整体趋势一致,误差原因是该阶段纤维不断的拔出或者断裂,试验结果不易测量准确。整体上,模型预测曲线与试验曲线吻合良好。

图6 ECC 受拉损伤演化曲线的验证Fig. 6 Verification of ECC tensile damage evolution curve
从图7 可以看出,试验应力-应变曲线在开裂前基本处于线性阶段,本文模型与三折线模型均与试验曲线吻合良好;在应变硬化与稳定损伤阶段,试验应力-应变曲线开始非线性上升,切线斜率逐渐减小直至达到峰值应力,本文模型相比于三折线模型在这一阶段能够表现出明显的非线性受力特征和较高的精度(尤其是图7(b)、图7(e)、图7(f)、图7(g)、图7(h)、图7(i));在应变软化与不稳定损伤阶段,试验曲线开始非线性下降直至试件断裂,这一阶段本文模型相比于三折线模型同样能够表现出非线性受力特征,但整体差别不大。
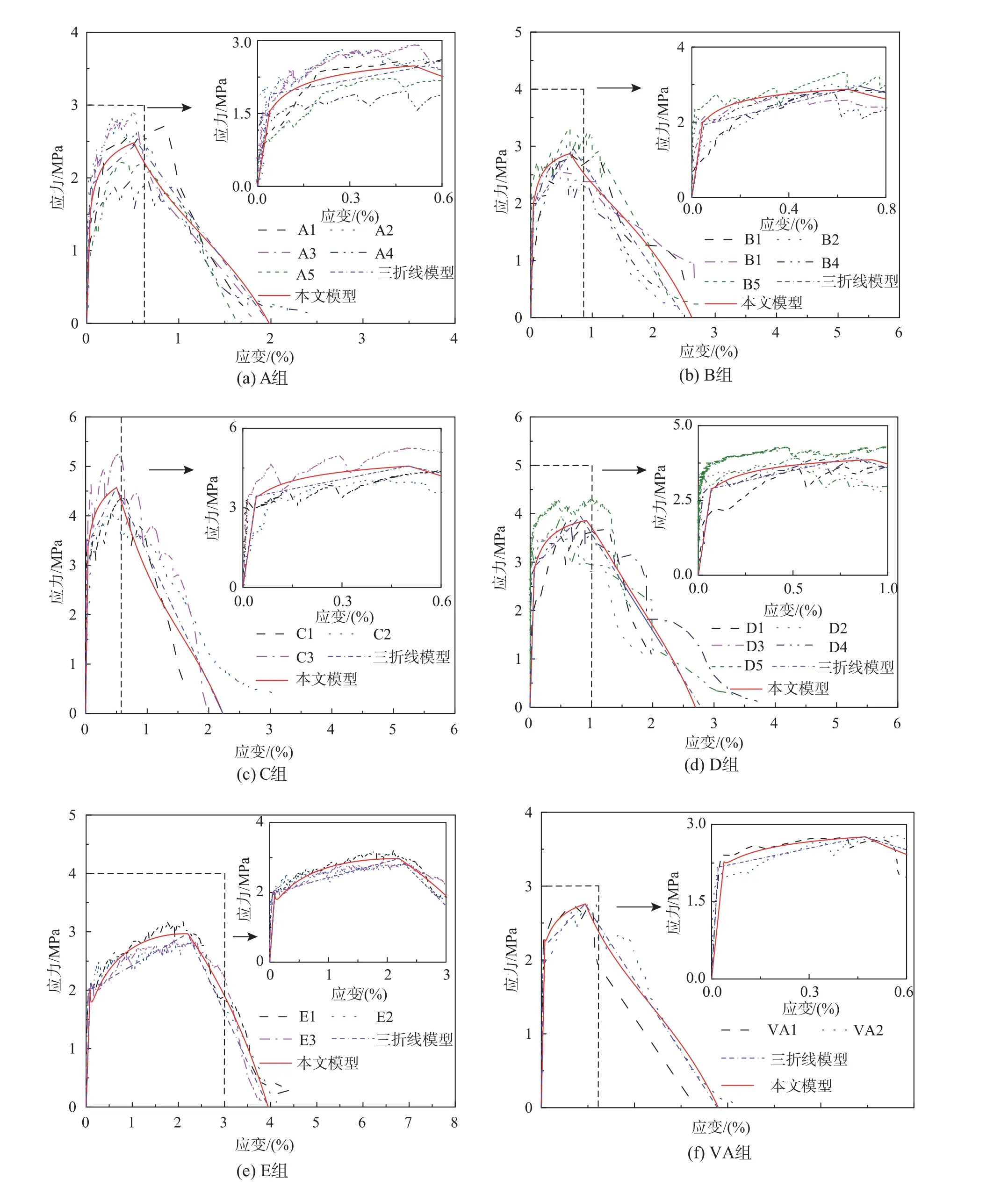

图7 ECC 受拉应力-应变关系验证Fig. 7 Verification of ECC tensile stress-strain curve
综上分析,本文所提ECC 受拉损伤本构模型能较准确地描述ECC 的受拉损伤发展全过程及其非线性应力-应变关系。
3 结论
通过对不同PVA 纤维体积掺入量和水胶比的ECC 试件单轴受拉试验研究,讨论了ECC 单轴受拉力学性能和全过程损伤机制,进而提出了ECC 受拉损伤本构模型,可以得出以下结论:
(1) PVA 纤维体积掺入量的增加能够显著增加ECC 的变形能力(PVA 纤维体积掺入量从1%增加至2%,峰值应变增加300%),但对强度影响不明显;水胶比的提高能够提高ECC 的变形能力(水胶比从0.24 降至0.28,峰值应变增加340%),但会降低ECC 的强度。
(2)基于ECC 受拉损伤机制的试验研究,以应力-应变曲线上一点与原点之间割线与横轴夹角变化程度表达ECC 受拉损伤因子,考虑PVA 纤维体积掺入量和水胶比的变化,结合试验数据给出ECC受拉损伤演化曲线方程(式(5)、式(9)~式(13)),进而得到ECC 受拉非线性应力-应变曲线方程(式(4))。
(3)基于本文对ECC 损伤因子和损伤演化方程的定义,对ECC 损伤演化方程求导分析表明:在应变硬化阶段,ECC 损伤逐渐增加,但损伤速率逐渐减小,损伤处于稳定发展阶段。在应变软化阶段,ECC 损伤和损伤速率均逐渐增加,损伤处于不稳定的快速增长阶段。
(4)与试验结果对比表明,本文模型能够较好的预测不同PVA 纤维体积掺入量(适用范围为0.01~0.02)和不同水胶比(适用范围为0.24~0.28)情况下ECC 的受拉损伤演化规律以及受拉非线性应力-应变关系,这将为更深入地研究ECC 及其在工程结构中的应用提供基础。诚然,限于本文参数范围有限,超出本文参数范围时仍有待进一步验证和修正。
