箱梁表面的压力分布对颤振稳定性的影响

刘祖军，贾明晓，杨詠昕

(1. 华北水利水电大学土木与交通学院，郑州 450011；2. 同济大学桥梁工程系，上海 200092)

箱梁是目前大跨度桥梁通常采用的截面形式。为提高其颤振临界风速，往往可以通过改变截面的气动外形来实现。但是箱梁的颤振与理想平板类似，多为弯扭耦合的颤振失稳形态，其发生的细观机理尚不够清楚。

SCANLAN 等[1]引入航空领域颤振导数的概念，将作用在振动断面上自激力表述为结构运动状态与颤振导数的线性组合，并根据结构动力学方法建立了颤振运动控制方程，形成了完整的桥梁颤振分析理论。后来的研究者多以此为基础，开展了桥梁的颤振性能研究。CHEN[2]提出的宏观机理分析方法可以采用非迭代的手段研究颤振导数对系统颤振性能的影响。MATSUMOTO 等[3−4]提出了分步分析方法求解耦合的颤振控制方程，并以此为基础，研究了多种断面的颤振导数和气动阻尼的变化规律。杨詠昕等[5]在Matsumoto 研究思路的基础上，导出了二维三自由度耦合颤振分析方法，并用该方法研究了箱梁的颤振机理。丁泉顺等[6]也采用类似方法，探讨了扁平箱梁颤振的发生机理。这些对箱梁颤振机理的研究侧重于分析颤振过程中颤振导数的变化规律。

除此之外，鲜荣等[7]采用风洞节段模型试验研究了风嘴、栏杆、检修轨道以及导流板对箱梁颤振稳定性的影响。金挺等[8]通过对箱梁表面测压数据进行积分的方法研究了箱梁断面的雷诺数效应。任若松等[9]也采用表面测压方法对准流线型桥梁断面的表面压力分布规律进行了研究。赵林[10]通过节段模型测压试验分析了在箱梁颤振过程中，模型表面压力分布特性的变化规律。孟晓亮等[11]通过节段模型测振试验和计算流体力学的方法，分析了不同风嘴角度对箱梁颤振和涡振性能的影响。张伟等[12]利用流场显示技术研究了箱梁断面颤振过程中，模型周围流场的变化情况。这些研究分析了箱梁颤振过程中压力场和流场的变化规律，但是没有阐明模型表面压力分布特性是如何影响箱梁的颤振导数以及颤振稳定性的。ARGENTINI等[13]提出的分布式非定常气动力表达方法则聚焦于表面风压对颤振和抖振的影响。 LI 等[14]采用微观机理分析方法，探讨了表面压力与颤振性能的联系，并绘制了气动阻尼的分布图。

从研究现状来看，目前从宏观和细观两个层面上都对箱梁的颤振机理进行了研究，但两个层面之间缺乏联系，很少将体现自激作用的颤振导数与模型表面的分布压力关联起来，因此也就缺乏对箱梁颤振机理深入认识。本文推导了颤振导数与模型表面压力之间的数学关系，研究了分布压力的空间作用位置以及相位分布特性对箱梁颤振导数和颤振临界风速的影响。通过对模型表面进行分区，研究了压力的局部特性对颤振导数和系统振动能量的影响。本项研究加深了对箱梁颤振发生机理的认识，为有效实施箱梁的颤振控制提供理论基础。

在空气中振动的桥梁断面，其运动状态与作用在模型上的自激气动力密切相关，而自激力是模型表面分布压力的合力。因此，为了深入理解箱梁断面颤振发生的本质就需要探讨箱梁颤振过程中模型表面分布压力的变化规律，并建立颤振导数与分布压力之间的数学关系式。

将推导模型表面分布压力与颤振导数之间的联系，通常采用8 个颤振导数来描述的气动升力和升力矩[15−17]，如式(1)所示：

1 颤振导数与表面压力的联系

1.1 颤振导数与表面压力的数学关系

式中：φα为气动力与模型扭转运动之间的相位差；x为沿模型宽度方向上的任意一点与模型中心之间的距离。

联立式(3)～式(4)、式(10)～式(11)，并通过比较系数可以求出H2∗、H3∗、A∗2、A∗3这4 个颤振导数：

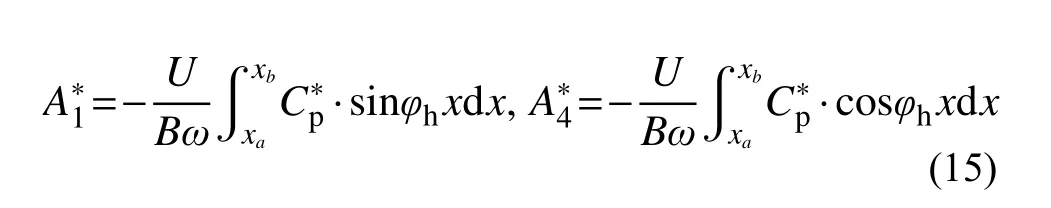
需要特别说的是本文在进行上述公式推导时假设桥梁颤振临界状态的振动形式为等幅的简谐振动。其主要是基于以下几点考虑：

1)目前对于桥梁―气流系统线性颤振临界状态的分析通常是认为当处于颤振临界点时，系统的阻尼为零，系统的振动为等幅简谐振动，气流输入到系统的能量刚好等于系统的阻尼耗能。例如：塔科马大桥在坠毁之前就经历的较长时间的扭转振动，较多学者在对该桥的颤振机理进行分析时也大多假设结构的振动为等幅的简谐振动。另外，在采用强迫振动试验确定颤振导数时，也通常是强迫断面做等幅的简谐振动，从而获得作用在断面上的气动力，进而识别颤振导数。因此本文基于现有的方法，仍假设桥梁―气流系统线性颤振临界状态的运动形式为等幅的简谐运动。

2)这一假设仅适用于桥梁发生小幅振动，并且不考虑系统非线性影响因素的条件下。对于线性系统而言，如果系统的振动位移为等幅的简谐振动，那么输入到系统的气动力也应该是简谐振动形 式，气动力与振动位移之间只存在相位差。由于气动力是模型表面压力积分之和，因此如果气动力是按照简谐振动方程的形式发生变化，则模型表面的分布压力也可以近似认为是按照同样的规律发生变化。但是如果强烈的流固耦合作用使得气动力具有较强的非线性时(气动力含有高阶成份)，这些假设条件就不再适用了。

1.2 数值实现途径

通过上述的理论分析可知，采用模型表面压力来求解颤振导数的关键是如何获取模型表面压力系数的幅值Cp∗和相位差φ，结合数值方法研究具体的实现过程，步骤如下(图1)：

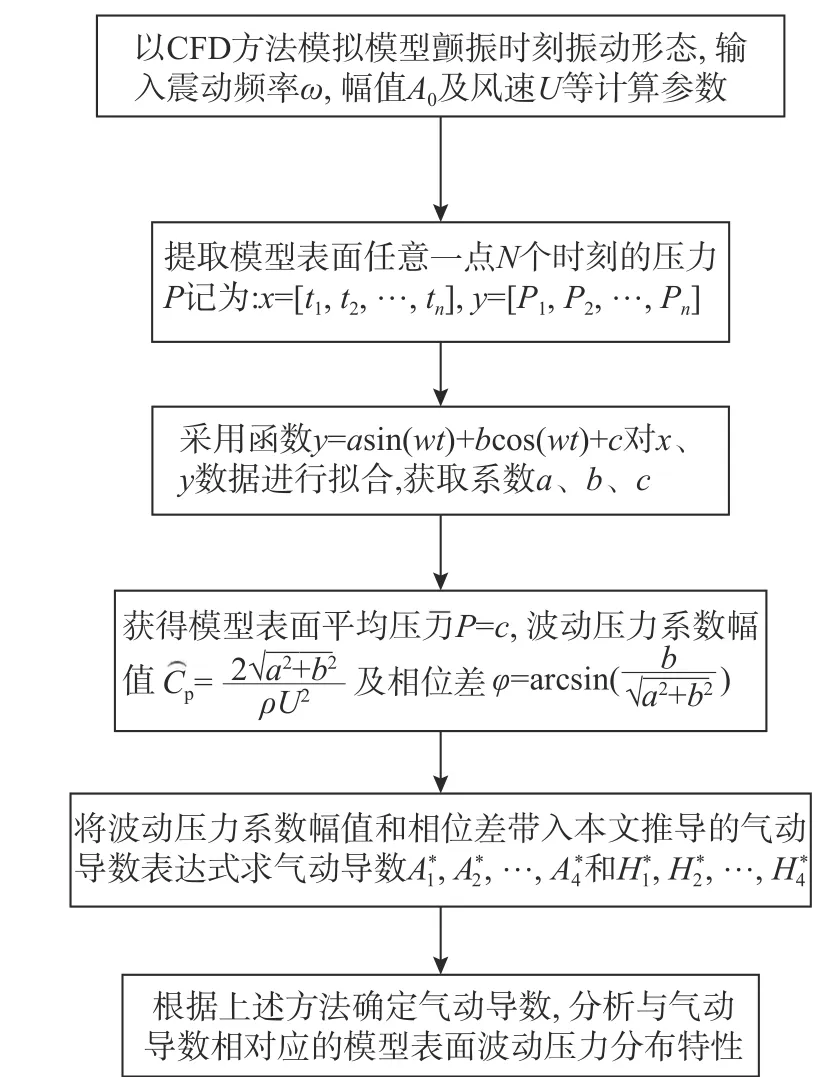
图1 数值实现途径Fig. 1 The process of numerical simulation

1)设定振动频率ω，振动幅值及来流风速，采用数值方法结合动网格技术模拟结构的强迫振动。

2)数值模拟时当结构运动状态达到平稳后，提取模型表面任意一点N个时刻的压力P，设x为n个 时刻，y为 与之相对应的压力P， 即：x=[t1,t2,···,tn]，y=[P1,P2,···,Pn]。

3)针对模型表面的任意一点，采用函数y=asin(ωx)+bcos(ωx)+c来拟合步骤2 中提取的N个时刻的压力值P，获得拟合函数的系数a、b、c。

上述建立了颤振导数与模型表面压力之间的联系，为分析模型表面压力分布特性对箱梁颤振稳定性的影响提供了基础。需要说明的是采用表面压力来描述颤振导数时，需要获得压力幅值Cp∗以及压力与振动位移之间的相位差φ。这里的相位差定义为箱梁表面压力的峰值与模型振动最大位移之间的相位延迟。

2 箱梁断面风致振动的数值模拟

根据上述建立的模型表面压力与颤振导数之间的数学关系，采用计算流体动力学方法(CFD)模拟了箱梁的强迫振动，提取了模型表面不同时刻的压力值，结合本文1.2 节中提出的分析方法，研究了分布压力对颤振导数的影响。

箱梁断面以大海带桥的主梁为原型进行了缩尺，其几何尺寸如图2 所示。应用商业软件Fluent进行数值模拟计算，计算域的选取如图3 所示，计算时壁面附近最小网格尺寸为0.0004 m，计算域采用分块结构化网格。网格数量为15.6 万。湍流模型采用基于RANS 方法的k−ωS S T两方程模型，压力速度耦合采用SIMPLE 算法，求解器采用分离式。基于流固弱耦合的计算策略和动网格技术分别模拟了箱梁的竖向和扭转强迫振动。

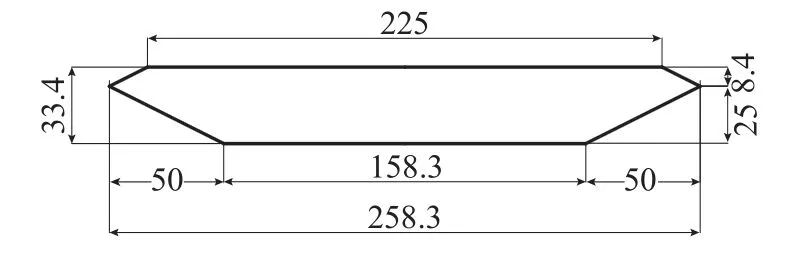
图2 箱梁断面 /mmFig. 2 The box girder section

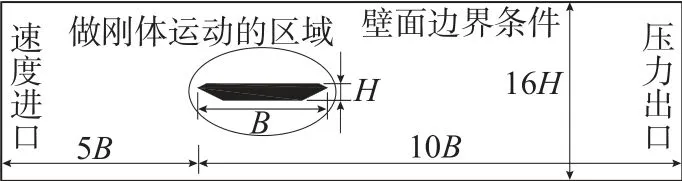
图3 二维计算区域及边界设置示意Fig. 3 Two-dimensional computational domain and boundary

结合该模型的颤振风洞试验结果，设置计算风速为20.8 m/s，竖向振幅为1.8 cm，扭转幅值为2.4°，振动频率为6.05 Hz。计算域的上端和下端设为壁面边界条件。计算时间步长取 ∆t=0.004 s，每次迭代计算的残差小于 10−5认为计算结果收敛。调整近壁面的第一层网格尺寸，使y+<5(图4)。

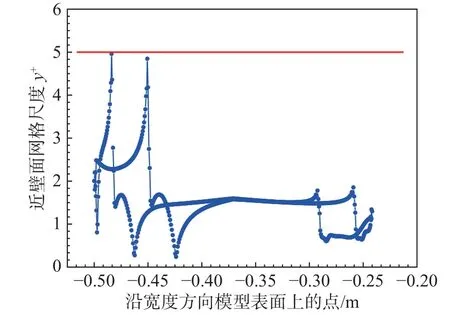
图4 模型断面近壁面网格的y+值Fig. 4 The grid value of y+ on the model surface

3 箱梁表面压力分布特性与颤振导数之间的联系

3.1 模型表面压力分布特点与颤振导数的关系

根据1.2 节中的方法，研究了箱梁表面压力分布特点与颤振导数之间的关系。模型运动的相位定义如图5 所示。为了说明数值拟合的精度，图6给出了模型分别处于平衡位置(T/2 时刻)，此时模型具有最大速度，以及模型运动到最大位移时(3T/4 时刻)，模型上下表面压力拟合的残差沿模型宽度方向的分布。从图6 可以看出，数值拟合的残差绝大部分在5%以内，只是在个别点处拟合的残差超过了5%，因此拟合的精度满足要求。另外，图7 给出了T/2时刻，模型上下表面压力的计算值与拟合值，从图中可以看出，二者之间吻合较好。

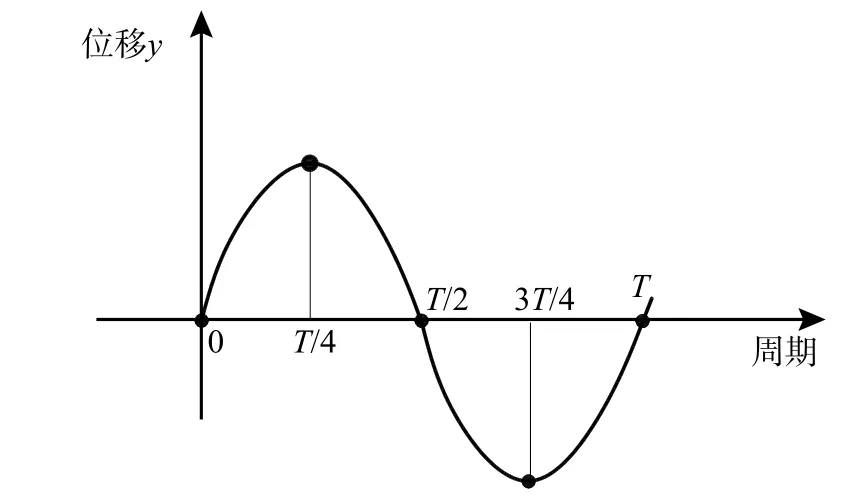
图5 模型的振动状态Fig. 5 The model vibration state

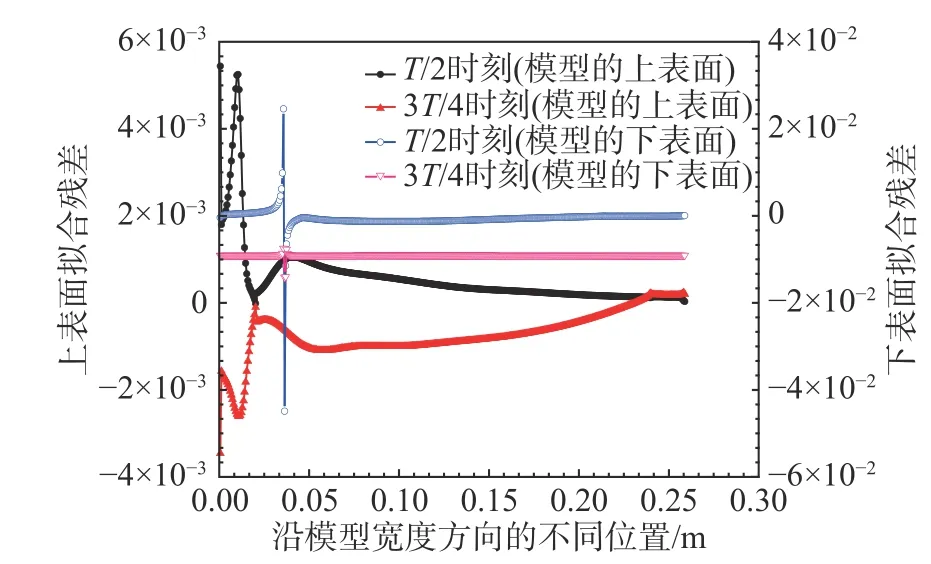
图6 压力数值拟合的残差在模型表面的分布Fig. 6 The pressure numerical fitting residuals' distribution on the model surface

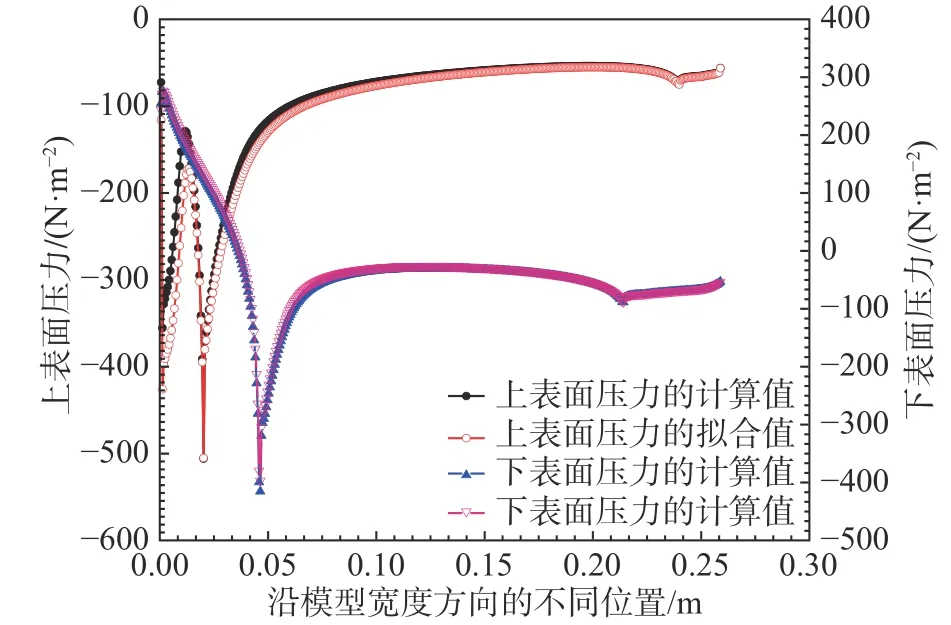
图7 模型表面压力的计算值与拟合值( T/2)Fig. 7 The model surface pressure calculation result and fitting values ( T/2)

上述分析说明了本文方法的有效性。根据CFD 计算获得的模型运动状态下的气动力，结合本文1.2 节中的方法，计算了拟合系数c沿箱梁表面的分布情况，如图8 所示。拟合系数c的分布情况代表了箱梁表面平均压力的分布特征。从图8可以看出箱梁迎风侧风嘴附近的平均压力较大，上下表面压力的分布规律类似，但力的作用方向相反。

图8 拟合系数c 沿模型表面分布图Fig. 8 The distribution of fitting coefficient c along the model surface

图10 给出了拟合系数b沿模型表面的分布情况，同图9 相比，二者的分布规律相似，也是在模型迎风侧风嘴所在区域数值较大，而在箱梁尾部所在区域数值较小。由于系数b的分布与气动导数A∗2直接相关联，因此箱梁迎风端的外形对颤振导数A∗2影响很大，而颤振导数A∗2对系统振动的稳定起到了非常重要的作用。

图9 拟合系数a 沿模型表面分布图Fig. 9 The distribution of fitting coefficient a along the model surface

图10 拟合系数b 沿模型表面分布图Fig. 10 The distribution of fitting coefficient b along the model surface

3.2 箱梁表面压力的局部特性对颤振导数的影响

通过3.1 节的分析可知在箱梁振动过程中模型表面压力的分布是不均匀的，模型表面的不同区域的分布压力对颤振导数的影响也是不相同，因此模型表面压力的局部特性对箱梁颤振稳定性产生的影响也不尽相同。因此，本节提出通过分块分析的方法来定量研究模型表面压力的局部特性对颤振导数的影响，模型表面分区如图11 所示。

图11 箱梁断面的分区示意图Fig. 11 The partition of H-shape section

根据CFD 数值计算结果，提取了箱梁断面在一个振动的周期内模型表面4 个分区上下表面压力差随计算时间变化关系，如图12 所示。从图12可以看出，在一个振动周期内，位于模型的迎风侧的3 区和2 区的压力差的变化随时间呈现出较明显的波动性，这与模型的周期性运动相对应。而位于模型背风侧的1 区和4 区的压力差基本上不随时间发生较大的变化。

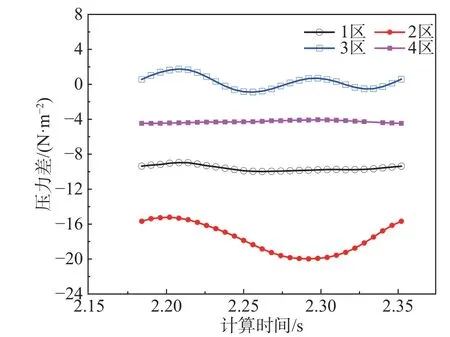
图12 箱梁断面不同区域的压力差Fig. 12 The pressure lag of different area on the box girder surface

结合建立的颤振导数与模型表面压力之间关系，讨论模型表面不同区域的分布压力对颤振导数的贡献。

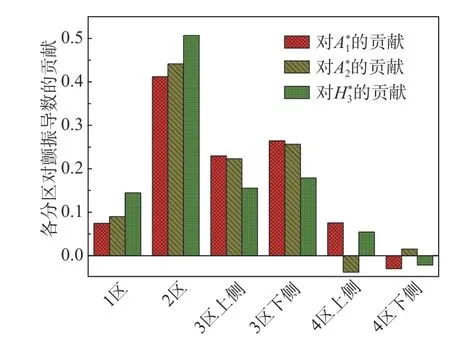
图13 模型表面各分区对颤振导数的贡献Fig. 13 Each partition contribution of the model to aerodynamic derivatives

通过计算模型表面不同区域输送给主梁的气动能量来更加清楚的说明模型表面分布压力的局部特性对主梁振动产生的影响。

一个周期内单位面积上的气动力输送给振动系统的非定常平均积累功w(x,t) 和功率N(t)的定义为：

式中：P(x,t) 为 结构表面的压力；v(x,t)为结构运动速度；n(x,t)为压力与速度之间的夹角。

根据式(21)计算了在一个振动周期内箱梁表面的不同区域输送给主梁的气动能量(图14)。迎风侧风嘴所在的3 区对模型输入的能量最大，2 区次之，相比之下1 区输入的气动能量则较小，而位于模型背风侧风嘴处的4 区输入给主梁的气动能量会由正变为负，因此有利于系统振动的稳定性。从这一分析结果可以看出迎风侧风嘴附近的分布压力对运动断面输入正能量，而背风侧风嘴附近的分布压力消耗运动断面的能量，因此在模型振动过程中，如果模型表面的主要分布压力向模型迎风侧移动，则气动力输入到系统的正能量逐渐增加，最终会导致模型振动稳定性的丧失。

图14 箱梁断面不同区域输送给振动系统的能量Fig. 14 The energy input to the system by the box girder different areas

4 探讨箱梁表面压力分布特性对颤振稳定性的影响

以上分析了箱梁表面压力分布特点与颤振导数的之间联系，以及分布压力的局部特性对颤振导数的影响，以此为基础来研究压力的分布特性是如何对箱梁颤振稳定性产生影响。为了便于说明问题，建立如图15 所示的箱梁断面的坐标系，靠近来流风场所在的箱梁区域为迎风侧，而靠近箱梁尾部的区域为背风侧。

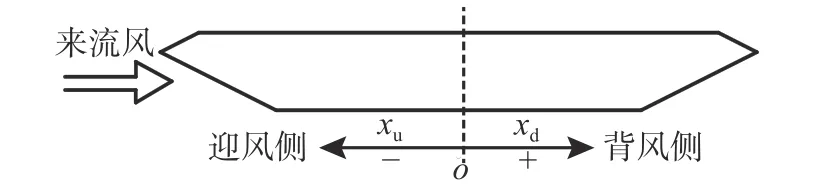
图15 箱梁断面的坐标系Fig. 15 The coordinate system of box girder

4.1 提高箱梁颤振稳定性所需要的压力分布特性

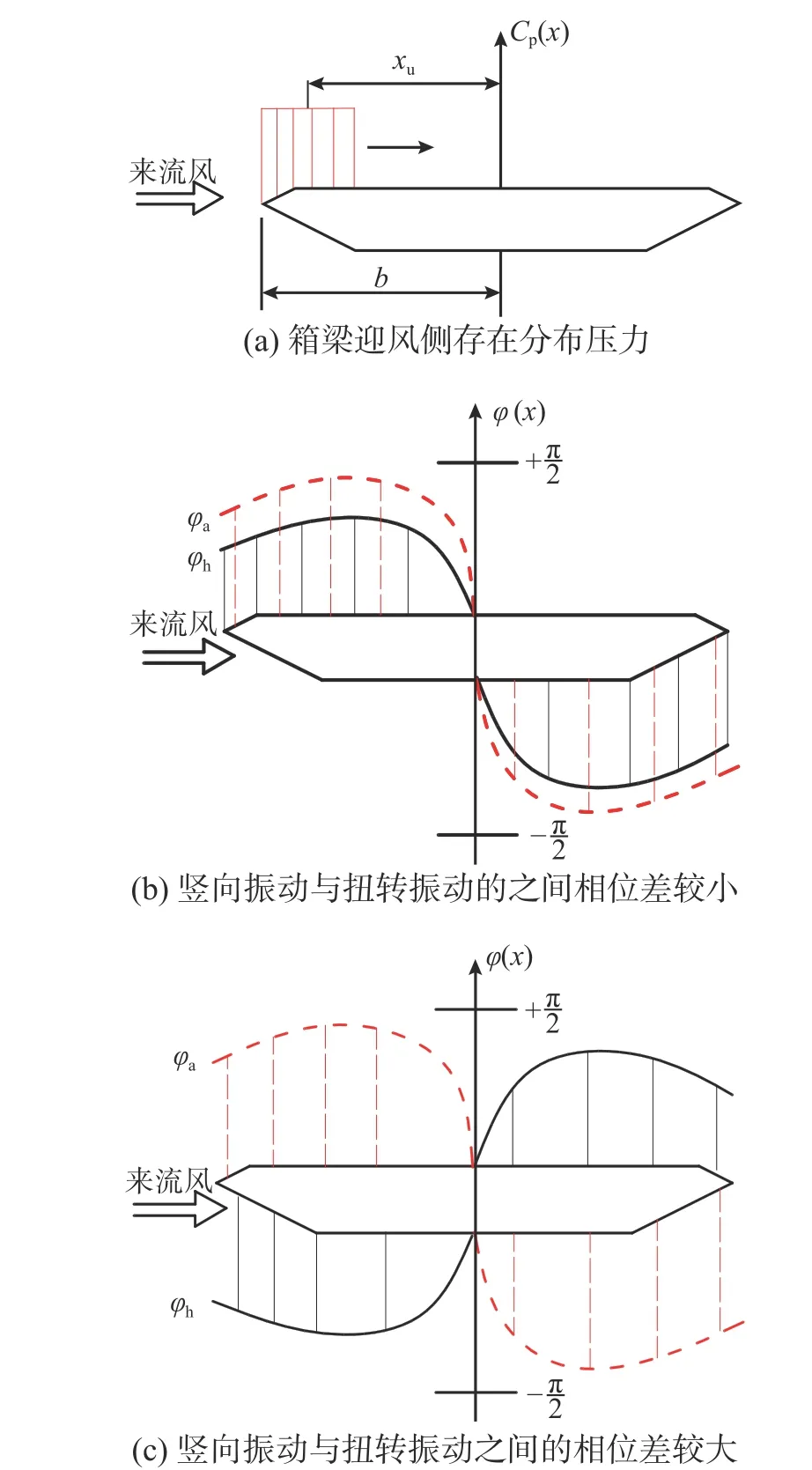
图16 箱梁表面压力和相位差的分布Fig. 16 The distribution of surface pressure and phase lag long the box girder

4.2 压力分布特性对箱梁颤振临界风速的影响

4.1 节初步探讨了为提高箱梁颤振临界风速所需的压力分布规律。结合箱梁模型的具体参数，根据假设的模型表面压力分布，应用本文的式(12)、式(13)计算颤振导数，通过二维耦合颤振分析方法，计算当分布压力处在模型表面不同位置，并且处于不同的相位差分布时箱梁的颤振临界风速。箱梁截面仍然采用如图2，纵向长度0.8 m。模型的基本参数如下：每延米的质量m=1.3625 kg/m，每延米的质量惯性矩Im=0.01277 kg·m2/m，竖向振动频率fh=2.825 Hz ， 扭转振动频率fa=7.452 Hz，竖弯阻比 ξh=0.0127 ， 扭转阻比 ξa=0.047。

首先分析分布压力的空间位置对模型颤振临界风速的影响。假设模型表面压力的分布范围是0.2b，压力的幅值Cp∗=10.0，压力中心距截面形心的距离xu分别为 − 0.9b、 − 0.4b、 0 .4b、 0 .9b(图17(a))。相位差呈对称分布，如图17(b)所示，在靠近迎风侧φa=π/3、φh=π/4 ； 而在背风侧φa=−π/3、φh=−π/4。根据上述压力分布规律，应用本文推导的颤振导数与分布压力之间的关系，可以计算出上述4 种压力分布情况下的颤振导数，应用二维耦合颤振分析，求得了与上述4 种压力分布状况相对应的颤振临界风速(图17(c))。从图中可以看出当分布压力位于模型的迎风侧时，箱梁的颤振临界风速最小，数值为16 m/s， 而当分布压力位于模型的背风侧时，箱梁的颤振临界风速最高，数值为36.5 m/s。因此，当箱梁表面峰值压力逐渐向模型尾部移动时，箱梁的颤振临界风速会逐渐提高。这也意味着如果箱梁尾部存在较强的压力作用则有利于箱梁颤振的稳定性。

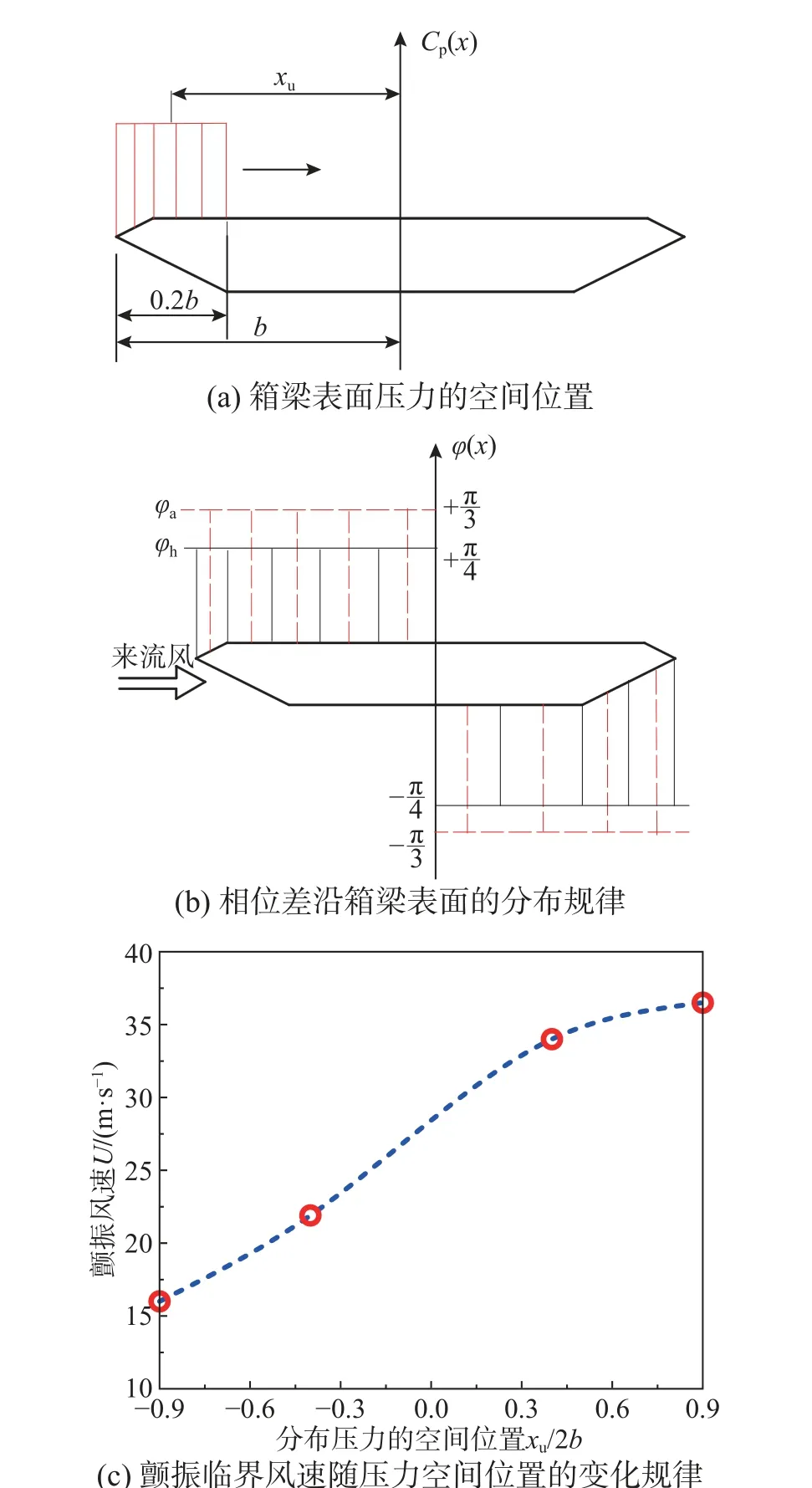
图17 箱梁表面的压力分布特性和颤振临界风速Fig. 17 The pressure distribution characteristics and flutter critical wind speed of the box girder

分析相位差的分布对箱梁颤振临界风速的影响，这里进行了两种情况下的计算：第1 种情况下，xu分别取为− 0.9b、− 0.4b、0 .4b、0 .9b，相位差呈反对称分布，在靠近迎风侧φa=π/3、φa=−π/4；在背风侧φa=−π/3、φh=+π/4，如图18所示。通过计算发现在这种相位差分布情况下，上述4 种压力分布状况对应的颤振临界风速高达288.8 m/s，也就意味着很难发生颤振失稳。

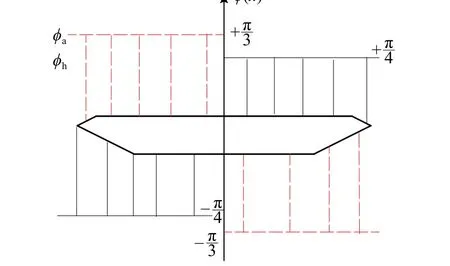
图18 相位差沿箱梁表面成反对称分布Fig. 18 The anti-symmetrically distributed phase lag along the box girder

第2 种情况下的计算条件为：−0.9b≤xu1≤−0.4b、0.4b≤xu2≤0.9b；相位差φa与φh分布规律相同，在迎风侧 π/6≤φa=φh≤π/2，在背风侧−π/2≤φa=φh≤−π/6。通过二维耦合颤振分析方法获得箱梁颤振临界风速如图19 所示。

图19(a)给出了当分布压力位于模型迎风侧时(−0.9b≤xu1≤−0.4b) 相位差由 π/6 变 化到 π/2的过程中，箱梁颤振临界风速变化规律。从图19(a)可以看出当迎风侧的分布压力向模型下游移动时，颤振临界风速逐渐增加。而当分布压力空间位置固定时，相位差由 π/6 变化到 π/2的过程中，箱梁颤振临界风速先增加后减小。

图19(b)给出了当分布压力位于模型背风侧时( 0.4b≤xu2≤0.9b) 相位差由 −π/2 变 化到 −π/6的过程中，箱梁颤振临界风速变化规律。从图19(b)可以看出当模型背风侧的分布压力向模型尾部移动时，箱梁的颤振临界风速增加；而当分布压力空间位置固定时，在相位差由 −π/2 变化到−π/6的过程中，箱梁颤振临界风速风速也不断增加。

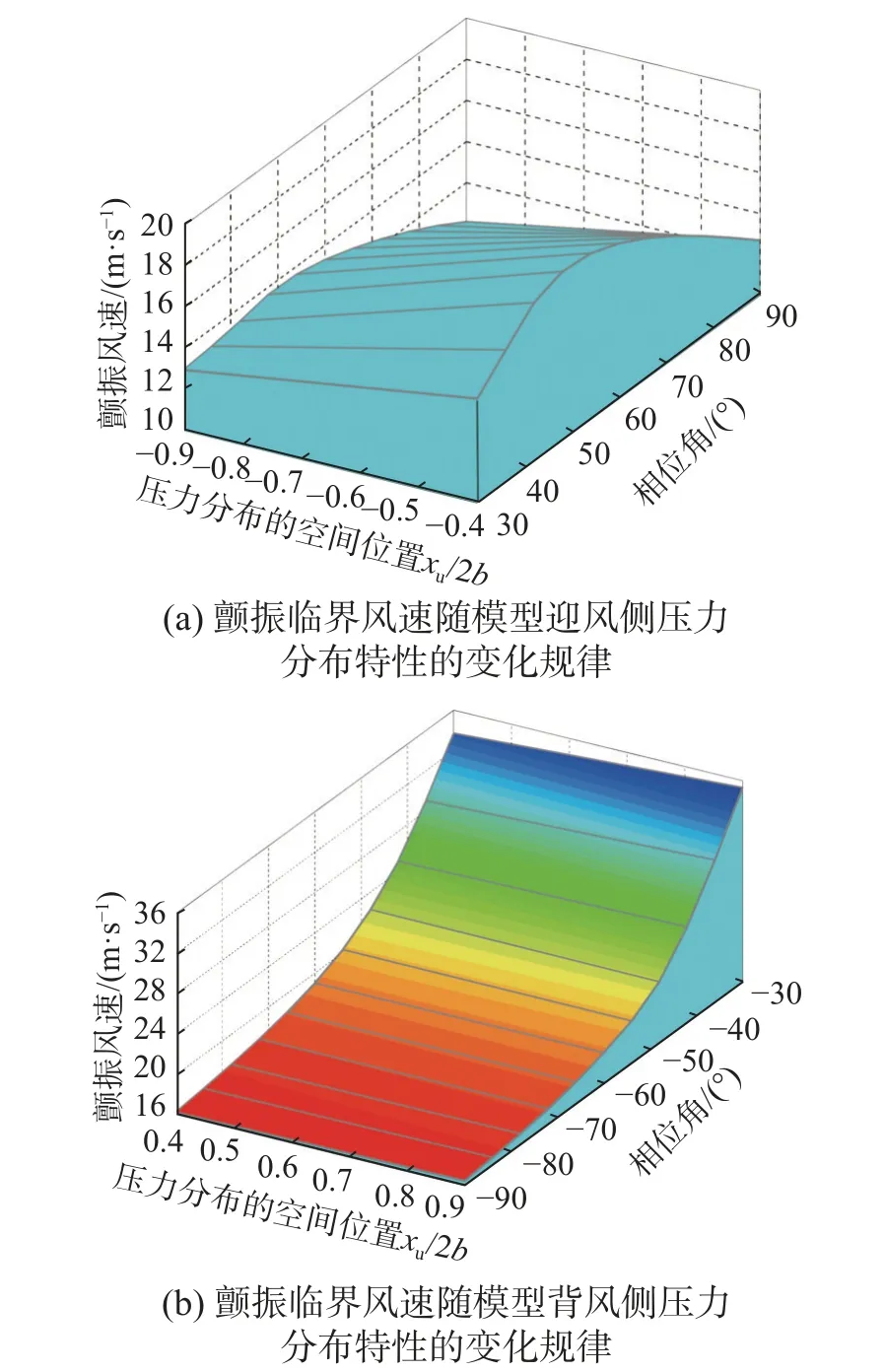
图19 颤振临界风速随箱梁表面压力分布特性的变化规律Fig. 19 The change of flutter critical wind speed with the distribution characteristics of the box girder surface pressures

通过探讨表面分布压力的空间位置和相位差对箱梁颤振临界风速的影响。可以得出一些启示：

1)颤振导数与模型表面压力的空间位置和相位差密切相关。在峰值压力向箱梁尾部移动过程中，颤振导数A∗1和A∗2的绝对值会不断减小，但是压力分布的空间位置对颤振导数H2∗和H3∗却没有影响。箱梁迎风侧的分布压力对模型的颤振稳定性起了不利的作用，而当迎风侧分布压力向模型尾部移动时，箱梁的颤振临界风速将会不断的提高。这也说明了如果箱梁尾部存在较强分布压力，则会有利于箱梁颤振的稳定性。

2)相位差的分布对所有的颤振导数都产生影响。相位差φa、φh呈反对称分布则能够对振动系统的稳定性产生有利作用，提高了系统的颤振临界风速。如果φa与φh的空间分布规律相同，那么当分布压力位于模型迎风侧时，颤振临界风速随相位差的增加先增大后减小；当分布压力位于模型背风侧时，颤振临界风速随相位差的增加而增大。

5 结论

本文建立了箱梁表面压力与颤振导数之间的数学关系式，应用CFD 数值模拟方法获得了箱梁振动状态下的表面压力，研究了箱梁表压力与颤振导数的联系，探讨了表面压力分布的空间位置和相位差的分布规律对箱梁颤振稳定性的影响。通过本项研究得出以下几点结论：

(1)对主要颤振导数A∗1、A∗2、H3∗贡献较大的是箱梁迎风侧风嘴所在的区域，并且决定A∗1和H3∗的表面压力的分布规律类似。当竖向振动与扭转振动的相位差不断减小时，决定A∗1和H3∗的表面压力的分布规律也就基本趋于相同，从而使得A∗1和H3∗的耦合作用更为强烈，因此，气动耦合效应与模型表面压力的分布特性密切相关。

(2)箱梁迎风侧风嘴及其附近区域的压力特性决定了箱梁主要颤振导数的性质，这对有效实施风振控制措施具有指导意义，通过合适的气动控制措施改变这些区域的流场特性，则能影响压力在这些区域的分布规律，从而提颤振临界风速。

(3)箱梁表面压力分布的空间位置对箱梁的颤振导数和颤振临界风速都有重要的影响。表面分布压力位于箱梁迎风侧时，则对箱梁的颤振稳定起了不利的作用，而当箱梁尾部存在较强的分布压力时，箱梁的颤振临界风速将会提高。当迎风侧的分布压力向箱梁尾部移动时，颤振导数A∗1和A∗2的绝对值会不断减小，而颤振导数H2∗和H3∗不受此影响，箱梁的颤振临界风速会逐渐增加。

(4)箱梁表面压力的相位差沿模型宽度的分布特性会对箱梁的所用颤振导数都产生影响。当表面压力与扭转和竖向振动最大位移之间的相位差φa、φh呈反对称分布时，系统的颤振临界风速较高。而当φa与φh的分布特性相同时，箱梁颤振临界风速随相位差的变化规律与模型表面压力所处的空间位置有较大关系。