输电线路防舞阻尼器系统参数分析及设计研究

黄赐荣，楼文娟，徐海巍，张跃龙

(浙江大学结构工程研究所，浙江，杭州 310058)

随着我国电网建设规模的日益扩大，导线的大幅度舞动问题容易造成混线短路、闪络跳闸、悬垂绝缘子线夹滑移、线路金具磨损、间隔棒断裂和引流线与跳线串分离等事故，严重影响电网的日常运作，甚至造成重大的经济损失[1]，因此对输电线路的舞动防治开展深入有效的研究具有重大意义。

导线舞动特性的影响因素非常多，包括风速、覆冰厚度、覆冰形状、风攻角、线路结构参数等，随着计算机技术的快速发展，导线舞动的机理、风洞试验、仿真模拟等方向的研究已经日趋完善，但有关防舞装置的设计和参数选择优化方法方面的研究仍不多见[2]，现有的防舞装置只能针对一种或几种特定的舞动形式，对于其他形式的舞动则抑制效果并不突出，甚至会增加其他形式舞动发生的概率。扰流防舞器利用特制的扰流线缠绕在导线表面，使得导线与扰流线合成体的各个截面位置的形状产生差异，从而让导线各个截面受到的气动力相互抵消，达到抑舞的目的，但其对于多分裂导线以及重覆冰导线的抑舞效果并不突出，扰流线在实际线路中的运用也存在很大的使用限制[3]。失谐摆，通过调整扭转频率来使之与竖向频率分离，从而防止导线发生竖-扭耦合舞动，在单导线的防舞中取得了很好的效果，但由于多分裂导线的扭转刚度、扭转变形并非线性分布，对于多分裂导线失谐摆的设计研究并不成熟[4]。回转式间隔棒通过部分取消线夹对子导线的扭转向约束使得导线覆冰因偏心扭矩转动，从而减弱导线覆冰的不均匀性，以此来达到防舞效果[5−6]，其防舞效果已在实际运行的线路上得到了验证，但回转式线夹等装置在真实环境的覆冰条件下由于轴承结冰，无法正常绕动，不能发挥其应有的防舞效果[7]。

输电线路发生舞动的直接原因是导线的总阻尼比(ξ=ξs+ξa)小于0[8−10]，即气动负阻尼比ξa的绝对值大于结构自身阻尼比ξs，所以通过提高导线线路的结构阻尼比ξs来解决导线舞动问题更加具有针对性。阻尼减振技术目前在桥梁抗风、建筑抗震等研究方向已被证明具有良好的减振效果，在输电线路中应用相对较少，目前典型的阻尼式防舞装置有粘弹性阻尼相间间隔棒，LOU 等[11]用粘弹性阻尼相间间隔棒替代相间间隔棒，并针对多个参数对舞动防治效果的影响进行了研究，验证了阻尼式防舞技术的良好防舞性能。现有研究表明导线舞动形式以竖向、竖-扭耦合舞动为主[2]，因此本文针对竖向舞动及竖-扭耦合舞动特点，提出了一种基于阻尼器的综合防舞方案，即通过在靠近输电塔位置的导线两端设置阻尼器来给线路系统提供附加阻尼，以达到抑制导线舞动的效果；并以某750 kV 实际多分裂输电线路为例，利用Hamilton 原理推导了整档线路-阻尼器系统的偏微分方程，运用多阶伽辽金函数进行自由度离散，并依据特征值分析得到导线-阻尼器系统的动力特性。在此基础上，分析了导线的垂度参数、阻尼器的安装位置、阻尼系数和刚度系数对系统阻尼比的影响。同时对比研究了粘滞阻尼器和负刚度阻尼器(NSD)对系统阻尼比的提升效果，并采用有限元仿真技术进一步对比了2 种阻尼器对实际线路舞动的真实抑制效果。

1 整档导线-防舞阻尼器系统运动方程的建立及参数分析

1.1 系统运动方程的建立

对整档输电线路-阻尼器系统建立运动方程，导线整体坐标系定义如图1 所示，阻尼器安装在离左侧和右侧耐张塔分别为xd1和xd2的位置，其中L为档距，y、z、 θ 分别为沿导线竖向、水平向、扭转向的坐标，m、EA、T分别为各子导线的单位长度质量、轴向刚度、初始张力；U为来流风速。导线的位移向量记为U=[u,v,w,θ]T，u、v、w、θ 分别为导线轴向、竖向、水平向、扭转向位移。根据Hamilton 原理得到导线运动的偏微分方程：

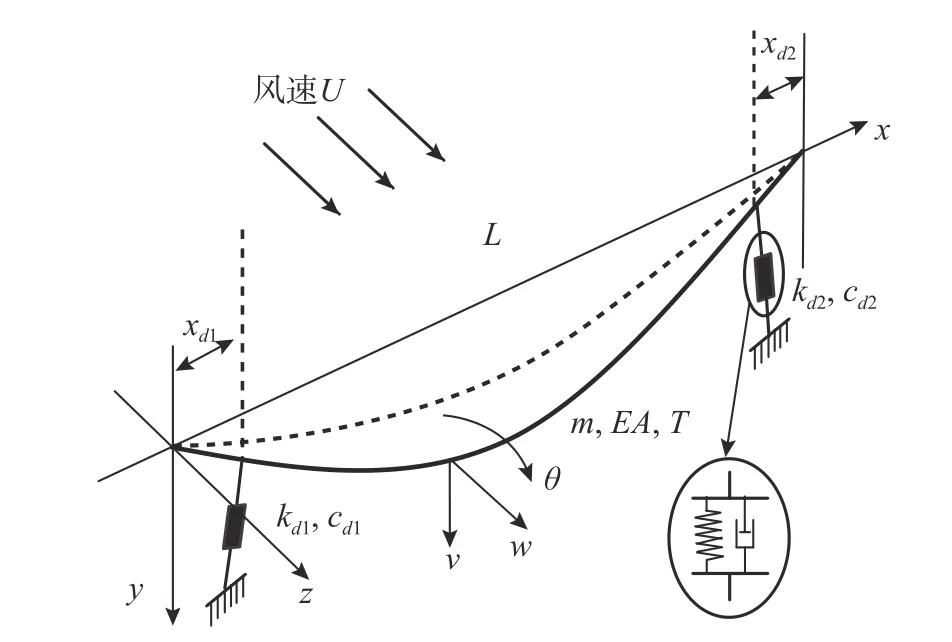
图1 输电线路-阻尼器系统振动模型Fig. 1 Vibration model of the transmission line-damper system

式中：Pdi为xdi位置处的阻尼器对导线作用的附加力；Vu、Vv、Vw、Vθ分别为轴向、竖向、水平向和扭转向的弹性势能；cu、cv、cw、cθ分别为轴向、竖向、水平向和扭转向的阻尼系数；fu、fv、fw、fθ分别为轴向、竖向、水平向和扭转向的风荷载；Sy、Sz为覆冰子导线相对y轴和z轴的面积矩；I为分裂导线截面转动惯量。

采用伽辽金方法，可以将上述偏微分舞动方程的解分解为伽辽金函数与广义位移时程的乘积：

式中，n为伽辽金函数的阶数。本文采用纯三角函数作为形函数：

将式(2)和式(3)代入式(1)，并乘以ϕj后沿导线轴向积分，可求得系统运动方程：

式中：M、C、K分别为质量矩阵、阻尼矩阵、刚度矩阵；q为广义位移向量；Fair为风荷载向量；Pdi为xdi位置处的阻尼器对导线的阻尼力和弹簧力之和，其具体形式如下：

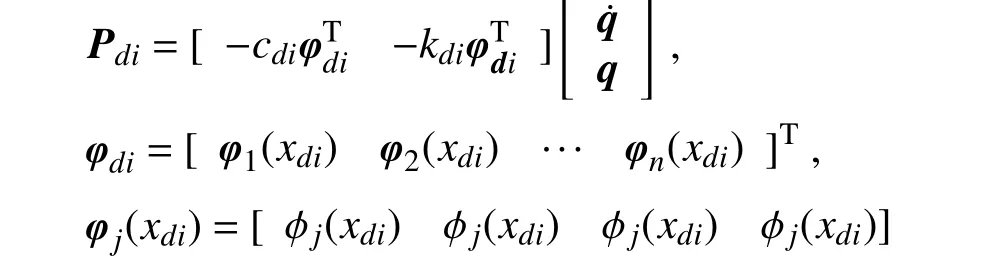
对Fair在q=0 处进行泰勒级数展开，忽略位移和速度2 次方以上项，获得气动荷载的线性化部分：

式中，Cair、Kair分别为由风荷载引起的气动阻尼、气动刚度矩阵，表达式如下：

由李雅普诺夫第一稳定定理可知，导线系统线性化运动方程的特征值实部为正时，导线会发生气动不稳定现象[12−14]。对式(4)进行特征值分析，可以得到导线-阻尼器系统的各个方向的动力特性参数(即自振模态阻尼比及自振频率)。为了获得运动方程式(4)的特征值，取Q=q˙，通过适当形式将上述二阶方程式(4)转化为一阶运动方程形式，令X=[Q,q]T，可以得到：

考虑到导线在靠近输电塔的位置安装了阻尼器，采用式(3)为振型函数时需要更高阶次的伽辽金函数，才能较为精确地表达系统的阻尼特性。

相应特征值λ 和特征向量x可由下式求得：

式中，ξjs、ξja分别为系统的第j阶等效结构阻尼比和风荷载引起的气动阻尼比。

当风荷载Fair为0 时，运动方程式(6)可简化为导线-阻尼器系统的自由振动方程，对应公式(8)的结果即为导线-阻尼器系统的等效结构阻尼比。

1.2 研究模型及方法

以某实际750 kV 单跨八分裂导线为例，采用运动方程式(6)对导线-阻尼器系统的动力特性进行计算分析。整档八分裂导线跨度为276 m，两端无高差，子导线型号为LGJ-500/45 其各物理参数列于表1。现有文献表明导线D 型覆冰更容易发生舞动现象[6,10]，因此本文研究的线路覆冰形状选择D 型覆冰。D 型覆冰形状最大覆冰厚度hice分别选择10 mm、15 mm、20 mm、25 mm 及30 mm以模拟现行国家标准《110 kV～750 kV 架空输电线路设计规范》[15]中导线由轻覆冰到重覆冰的不同工况，具体覆冰形状以及参数参考图2。

表1 子导线物理参数表Table 1 Physical parameters of sub-conductors

图2 覆冰导线气动力受力图Fig. 2 Aerodynamic force of iced conductor

为了给出合理的伽辽金分解形式，对取不同伽辽金阶数下系统的一阶等效结构阻尼比的计算结果与数值模拟结果进行了比较，其中有限元数值模拟结果由有限元阻尼模态分析得到。由图3可以发现，当伽辽金阶数n>60 时，计算阻尼比结果基本收敛，且与有限元数值模拟结果吻合较好，可以认为计算阻尼比可以反映系统的实际阻尼比。因此，为了兼顾计算效率及计算结果的准确度，本文后续的计算中伽辽金分解的阶数均取80。

图3 不同伽辽金阶数下的系统一阶等效阻尼比Fig. 3 First-order equivalent damping ratio of system under different Galerkin orders

1.3 系统参数分析

1.3.1 线路垂度参数的影响

为了研究线路自身特性对阻尼器设置的影响，引入无量纲线路垂度参数[16]：

式中，f为线路跨中位置处的垂度。

令相同阻尼系数的2 个阻尼器对称安装在距离导线两端L/10 位置处。对于本文研究的5 种覆冰厚度工况，导线系统相应的垂度参数η 分别为130、153、175、205、240。对上述不同垂度参数下导线-阻尼器系统前三阶等效结构阻尼随阻尼器阻尼系数的变化情况进行计算分析。考虑到不同阻尼器刚度系数下，系统等效阻尼比随阻尼器阻尼系数的变化趋势相似，为了研究线路垂度参数对系统阻尼比的影响，采用了恒定的阻尼器刚度系数，即取K=0。相应计算结果绘于图4 和图5。

图4 不同垂度参数下的一阶等效阻尼比Fig. 4 First-order equivalent damping ratio of system under different sag parameters

由图4 可知，导线-阻尼器系统的一阶阻尼比对线路的垂度参数变化非常敏感。随着线路垂度参数的减小，系统的1 阶模态最大阻尼比会呈现增长趋势。由图5 可知，线路垂度参数对高阶(二阶、三阶)模态阻尼比的影响并不明显，且不同垂度参数下高阶模态的最大阻尼比均可达到15%左右，足以抑制导线高阶模态舞动。现有文献研究[9]表明，导线一阶舞动相对于高阶舞动更容易被激发，且舞动能量也主要集中于一阶模态，所以本文后续将主要将以提升系统的一阶等效结构阻尼比为目标对阻尼器的安装位置、阻尼系数和刚度系数进行优化设计。

图5 不同垂度参数下的系统高阶等效阻尼比Fig. 5 High-order equivalent damping ratios under different sag parameters

1.3.2 阻尼器阻尼系数分析

阻尼系数是阻尼器设计的重要参数，将会对导线-阻尼器系统的动力特性产生较大的影响。导线两端的阻尼器安装形式可以分为对称安装、不对称安装2 种。下面将针对这两种安装形式，考察系统的一阶阻尼比随导线两端阻尼器的阻尼系数Cd1、Cd2的变化情况。计算时阻尼器刚度系数K仍为0。

图6(a)和图6(b)分别给出了双阻尼器不对称安装(xd1=L/15 ，xd2=L/10)、对称安装(xd1=xd2=L/10)在线路两侧时，系统的一阶等效阻尼比随双阻尼器的阻尼系数变化趋势图。由图6 可以发现，无论对称还是非对称安装，系统的一阶阻尼比在阻尼系数空间(Cd1,Cd2)中均存在唯一的最大解ξmax，将最大ξmax所对应的阻尼系数组合定义为最优阻尼系数(Cd1-opt,Cd2-opt)。当上述阻尼器不对称安装时，Cd1-opt的值并不等于Cd2-opt，而当阻尼器对称安装时，Cd1-opt与Cd2-opt相等。

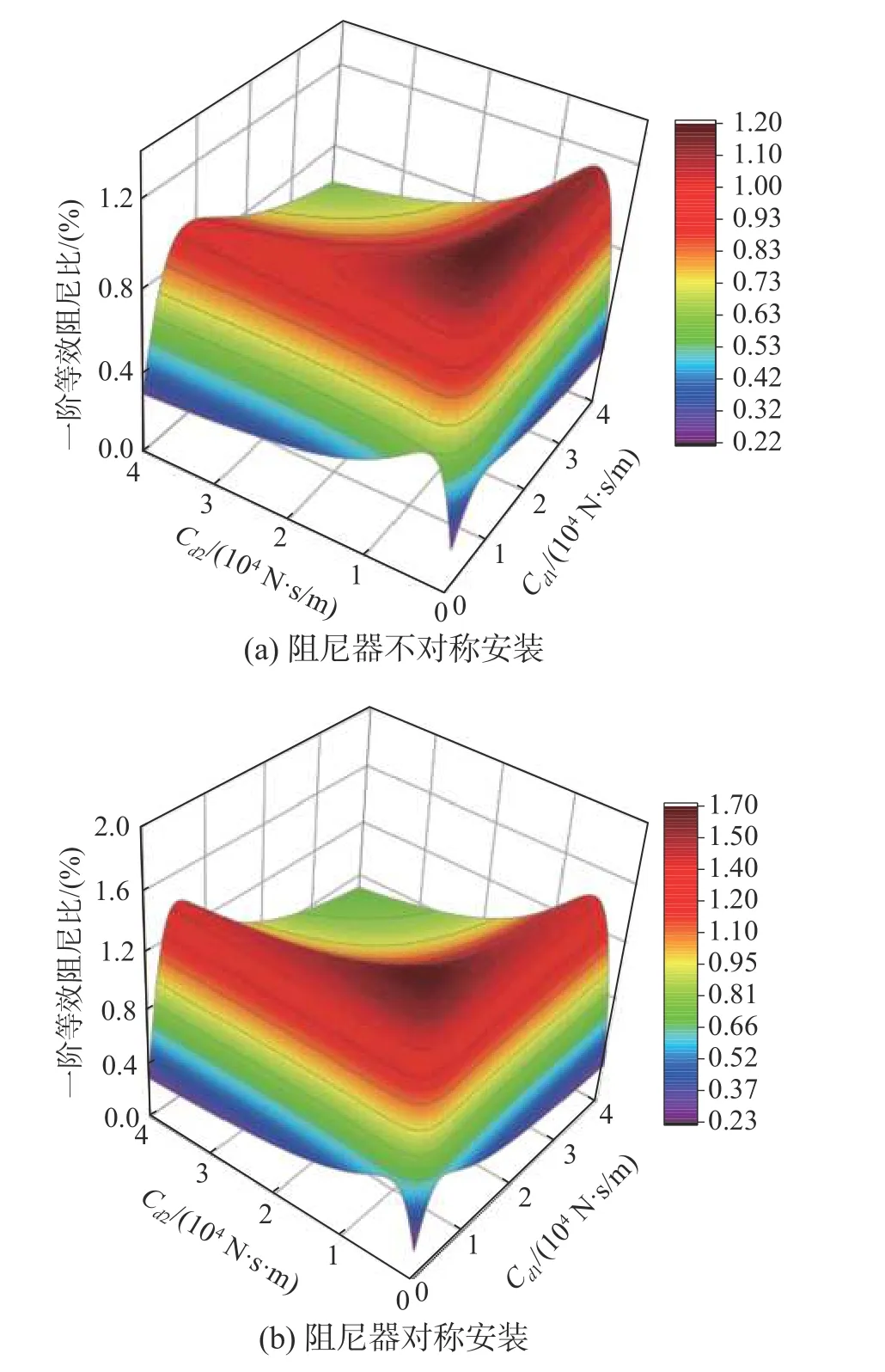
图6 不同阻尼器安装形式下的系统一阶等效阻尼比Fig. 6 The first-order equivalent damping ratio of the system under different installation forms of dampers

1.3.3 阻尼器安装位置分析

阻尼器的安装位置不同，系统所能达到的最大一阶阻尼比ξmax也会相应发生改变，最大解ξmax所对应的最优阻尼系数组合也会产生显著差异。考虑到阻尼系数越大阻尼器的制作难度也会更大，因此，阻尼器位置选择应在尽可能增大系统一阶最大阻尼比的同时应尽量减少最优阻尼系数值。为了便于阻尼器的实际应用与安装，本文将阻尼器安装的位置选择为距离导线两端[L/15L/10]的区间范围，以便与塔身进行可靠连接。对不同阻尼器位置下(阻尼器刚度系数K=0)，系统所能达到的一阶模态最大阻尼比及最优阻尼系数组合中的较大值max(Cd1-opt,Cd2-opt)进行了计算分析。相应结果分别列于图7(a)和图7(b)。

由图7(a)可知，系统的一阶最大阻尼比ξmax会随两侧阻尼器的安装位置发生变化，任意一侧阻尼器越靠近跨中，系统所能达到的一阶最大阻尼比也越大。而由图7(b)可知，当阻尼器对称安装时，最优阻尼系数(Cd1-opt,Cd2-opt)中的较大值相比非对称安装时更小，且对称安装时两侧阻尼器的最优阻尼系数保持一致，有利于阻尼器的统一加工。

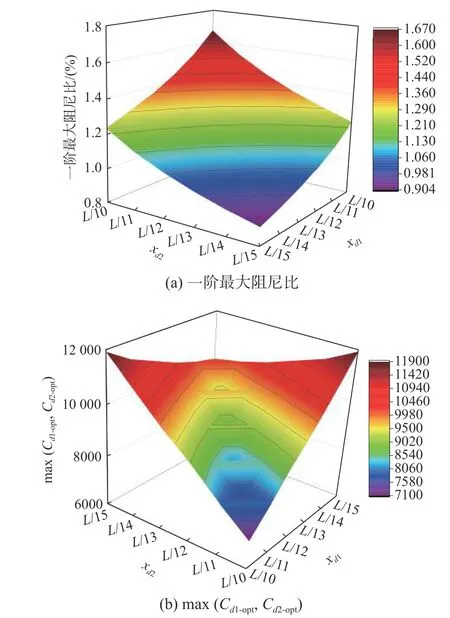
图7 不同阻尼器安装位置下的系统动力特性Fig. 7 Dynamic characteristics of the system under different damper installation positions

根据上述研究可知，阻尼器越靠近跨中安装，系统的阻尼比提升效果越好，但实际线路中，为了阻尼器安装和拆卸方便，阻尼器的安装位置不能无限靠近跨中，需要对阻尼器安装位置进行限制。依据本文算例，建议阻尼器安装在最大限制距离位置即L/10 处，此时得到的阻尼比最优，且阻尼器所需要的阻尼系数也最小。

1.3.4 阻尼器刚度系数分析

桥梁拉索等相关研究中已经证明阻尼器的内刚度对系统的减振效果具有不利影响[13]，阻尼器的刚度越小，阻尼器的减振效果越好。目前，负刚度阻尼器(NSD)在建筑、桥梁防灾减振相关研究中已经被证明可以发挥良好的减振效果[17−18]，但其在输电线路防舞方面仍缺乏相关研究。为了验证NSD(K<0)与传统的粘滞阻尼器(K=0)、粘弹性阻尼器(K>0)的防舞性能差异，本节对不同垂度参数下的导线-阻尼器系统的的最大一阶阻尼比、最优阻尼系数和一阶自振频率随阻尼器内刚度的变化规律进行了研究。图8 给出了阻尼器对称安装于距导线两端xd1=xd2=L/10 位置处的结果。

图8 不同垂度参数下的系统动力特性Fig. 8 Dynamic characteristics of system under different sag parameters

如图8(a)所示，当阻尼器的刚度大于0 时，导线-阻尼器系统的一阶最大阻尼比呈减小趋势，表明粘滞阻尼器(K=0)对系统一阶阻尼比的提升效果好于粘弹性阻尼器(K>0)。当阻尼器刚度为负，即K<0 时，阻尼器对系统一阶等效阻尼比的提升效果相比粘滞阻尼器显著增加，且存在一个最优负刚度kopt使得系统一阶阻尼比可以达到最大。负刚度阻尼器可使得一阶阻尼比最大提升至原始线路结构阻尼比的100 倍左右，而传统的回转式间隔棒对阻尼比的最大提升效果仅为原结构值的25 倍左右[6]。由图8(b)可知，在最优负刚度kopt时，阻尼器达到一阶最大阻尼比所对应的最优阻尼系数也是最小的，这与前文的结论是一致的；而图8(c)则显示，当选用NSD 阻尼器时(即K<0)时，系统的一阶自振频率相比粘滞阻尼器也会明显降低，更低的自振频率意味着对导线的破坏也将更小，能减小导线舞动发生断线的可能性[19]。

考虑到NSD 阻尼器相比传统阻尼器的优势，对其处于不同的对称安装位置时(安装位置xd1=xd2=L/10、L/12 、L/15)的效果开展进一步研究。图9 给出了不同刚度NSD 下导线系统的一阶最大阻尼比和自振频率。图9(a)可以发现，阻尼器位置从L/10 变换到L/15，系统的一阶最大阻尼比仅从18.4%下降到16.8%左右，表明其受阻尼器位置的影响较小。但安装位置越靠近跨中，导线-阻尼器系统的最优负刚度kopt值(绝对值)越小。而由图9(b)可知当NSD 阻尼器安装在不同位置时，系统的一阶自振频率均在kopt达到最小值，且不同位置处的最小一阶自振频率幅值基本相等。由此可见，最小一阶自振频率对于NSD安装位置也不敏感。

图9 不同NSD 安装位置下的系统动力特性Fig. 9 Dynamic characteristics of system under different NSD installation positions

2 防舞阻尼器设计

导线的气动稳定性与风速、风攻角密切相关。在特定的风速和风攻角下，当导线-阻尼器系统的等效结构阻尼比小于舞动的临界阻尼比时，系统在该风攻角下会产生气动失稳。

已有研究表明，输电线路在低风速下更易发生舞动，且导线的舞动基本上以前三阶模态为主[17]。本文选择风速研究区间为0 m/s～27 m/s(风速计算间隔取0.2 m/s)，线路参数参考表1。覆冰形状选择D 型覆冰的30 mm 厚度工况。其中覆冰导线的气动力参数根据以往的风洞试验结果获得[9]，如图10所示。根据式(6)可以获得不同风速工况下的竖向前三阶特征值，并通过特征值实部的正负对输电舞动稳定性进行判断。根据特征值计算发现该覆冰线路舞动风攻角区域基本集中在62°～79°和167°～180°区域。

图10 覆冰子导线的三分力系数Fig. 10 Three-component force coefficients of iced sub-conductor

对上述易舞风攻角范围内不同风速下的前三阶竖向舞动临界阻尼比进行计算，对于给定风攻角，选择计算风速区间内的临界阻尼比最大值作为该风攻角下的舞动临界阻尼比。图11 给出了舞动风攻角范围内的前三阶竖向舞动临界阻尼比。为了能够抑制所有风攻角下导线的舞动，选择各风攻角临界阻尼比中的最大值作为整个线路的舞动临界阻尼比，由此得到该线路前三阶竖向舞动的临界阻尼比分别为2.63%、3.08%、5.37%，如图11 所示。当导线-阻尼器系统的等效结构阻尼比大于舞动临界阻尼比时，系统将不会发生舞动。根据式(8)可知，在线路端部安装阻尼器后，导线系统的等效结构阻尼比ξj-s将大幅度提高，在部分易舞风速下，系统的总阻尼比会将不会出现负值，从而抑制了导线在该风速下发生舞动。相当于提高了导线起舞的临界风速。例如在171°风攻角下，根据式(8)计算可知，安装粘滞阻尼器前后系统的起舞风速分别为3.42 m/s 和12.56 m/s，起舞风速得到明显提高。

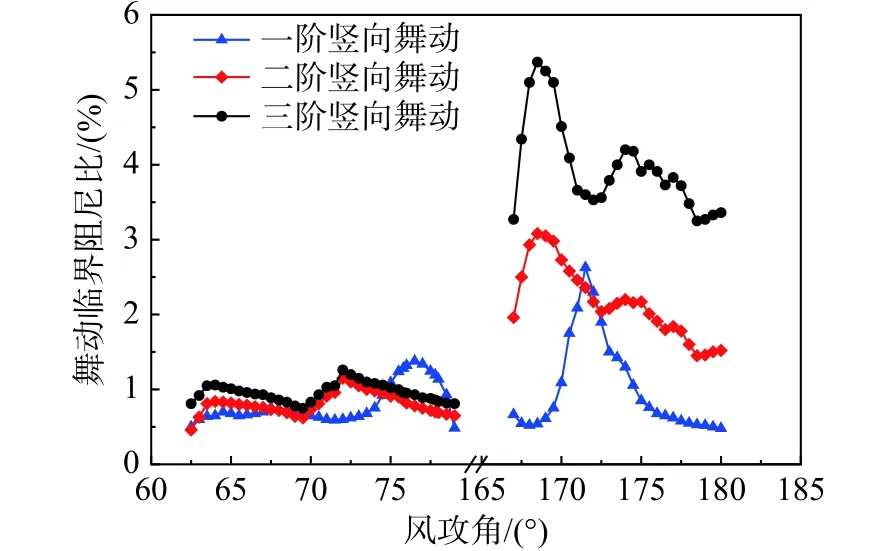
图11 各风攻角下的舞动临界阻尼比Fig. 11 Critical damping ratio of galloping under various wind attack angles

由1.3.4 节参数分析已知粘滞阻尼器对于导线系统阻尼比的提升效果明显优于粘弹性阻尼器，因此本节仅选择粘滞阻尼器和NSD 进行对比研究。粘滞阻尼器的刚度为K=0；NSD 的刚度则应根据系统阻尼比满足不发生舞动所需的值(即超过临界阻尼比)进行确定，为了发挥最佳的防舞效果，导线-NSD 系统的等效阻尼比应大于舞动临界阻尼比，因此针对本文的计算线路(一阶舞动临界阻尼比为2.63%)选择NSD 的刚度为K=−8000(一阶等效阻尼比为2.86%)，在此刚度下，NSD 不仅可以发挥良好的防舞效果，也有利于NSD 的制作(NSD 负刚度越小，NSD 制作难度及成本越低)。

为了验证本文理论计算方法的正确性，如图12(a)所示，设计了输电导线-电涡流阻尼器(粘滞阻尼器)系统的室内大比例缩尺试验模型，通过导线-电涡流阻尼器系统的自振试验测定了系统的一阶等效阻尼比，并对理论计算值进行对比验证。由图12(b)可知，当线路安装粘滞阻尼器时，系统一阶等效阻尼比的理论计算值与试验值吻合较好，阻尼比随阻尼器阻尼系数的变化趋势基本一致，验证了本文的理论计算方法的正确性。图12(b)和图12(c)给出了不同阻尼器参数下系统的前三阶阻尼比的理论计算结果，可以发现NSD 相比粘滞阻尼器，对系统各阶阻尼比的提升效果都更加优秀，尤其是一阶阻尼比，当K=−8000 时，系统一阶最大阻尼比可以达到2.86%，大于该线路的一阶舞动临界阻尼比，可以完全抑制导线所有风攻角下的一阶舞动，而安装粘滞阻尼器后的最大阻尼比远小于舞动临界阻尼，只能抑制部分风攻角下的舞动。两种阻尼器对高阶阻尼比的提升效果都远大于该线路高阶舞动的临界阻尼比，因此对于高阶舞动两者均具有较好的抑制效果。此外，导线-NSD 系统的前三阶最大阻尼比所对应的最优阻尼系数Copt-1、Copt-2、Copt-3取值更为接近且取值也最小，有利于阻尼器的阻尼系数选取。

图12 两种阻尼器对系统阻尼比的提升情况Fig. 12 The improvement of damping ratio by two kinds of dampers

通过前述分析可知，NSD 对系统各阶阻尼比的提升效果远好于传统粘滞阻尼器，因此针对该阻尼器给出相关的参数设计原则，以便服务于工程应用。首先，阻尼器安装时可以优先考虑与输电塔塔臂的可靠连接。阻尼器的布置形式宜选择两侧对称布置，其安装位置在满足阻尼器实际安装技术工艺、线路安全、电气绝缘要求的前提下尽可能远离导线两端，如本文算例建议选xd1=xd2=L/10。其次确定阻尼器刚度，取kopt时，系统达到最大阻尼比且其对应的最优阻尼系数和一阶频率也达到最小，是较为理想的情况。但考虑到，kopt附近将发生频率的突变(如图8(c))，为了避免频率突然增大的情况发生同时兼顾系统阻尼比以及最优阻尼系数，建议NSD 的刚度系数不高于|0.9kopt| 。根据所选择的阻尼器刚度，阻尼系数选择系统一阶最大阻尼比所对应的最优阻尼系数Copt-1。

3 不同阻尼器抑舞效果对比

根据现有研究，运用ANSYS 软件可以较为精准地模拟覆冰分裂导线舞动[10]。为了进一步验证不同阻尼器方案的防舞效果，本节利用ANSYS 有限元仿真技术研究了原型线路在导线两端近塔区(xd1=xd2=L/10)对称安装粘滞阻尼器和NSD 前后的导线风振响应时程。针对第2 节中的不利覆冰线路进行分析，两种防舞阻尼器的参数选择如表2所示，以达到各自最优的设计效果。仿真模拟过程中，导线单元和间隔棒单元均采用BEAM188 进行模拟，导线单元取为1 m 长度，共布置5 组间隔棒，两端支座采用固支形式，即距两端支座27.6 m的跨中部分等间距设置5 组间隔棒，利用Endrelease 命令对每个子导线单元释放BEAM188 单元的弯曲自由度，以保证6 自由度的间隔棒单元与4 自由度的子导线单元在ANSYS 软件中可以自动实现自由度缩聚，进而耦合导线4 个运动方向的状态。由于COMBIN14 单元可以模拟线性阻尼单元与刚度单元并联的情况，阻尼器采用COMBIN14单元进行模拟，计算时相对风速、风攻角、气动力系数随运动状态的改变进行更新迭代加载。图13和图14 给出了77°和171°两个易舞风功角下导线在加装不同阻尼器前后的响应时程。两种工况下的计算风速分别为9 m/s (77°)和15 m/s(171°)。

表2 防舞阻尼器设计参数Table 2 Design parameters of anti-galloping damper

由图13(a)可以看出，伽辽金法得到的舞动幅值与ANSYS 模拟得到的幅值基本吻合，证明有限元仿真模拟可以较为精准地模拟覆冰分裂导线舞动。由图13 的结果对比可知，两种不同参数的阻尼器均能有效抑制导线舞动，但相比粘滞阻尼器，NSD 能更快的抑制舞动。由图14 可以发现，粘滞阻尼器可以提高系统的等效阻尼比，导线舞动的起舞时间明显延长，舞动幅值也有所下降，但导线舞动不能被完全抑制，而采用NSD 则能完全抑制导线舞动。

图13 77°风攻角下安装阻尼器前后防舞效果对比Fig. 13 Comparison of anti-galloping effects before and after installing dampers under 77° wind attack angle

图14 171°风攻角下安装阻尼器前后防舞效果对比Fig. 14 Comparison of anti-galloping effects before and after installing dampers under 171° wind attack angle

4 结论

本文提出了一种通过在导线两侧靠近输电塔位置处安装阻尼器来实现舞动防治的目的。研究了导线垂度、阻尼器安装位置，刚度系数和阻尼系数等对系统阻尼的影响。通过数值算例分析和有限元仿真考察了2 种不同阻尼器的抑舞效果并给出了相应的阻尼器设计方法，主要结论如下：

(1) 阻尼器在不同安装位置下，导线系统的一阶等效阻尼比均存在一个最大解ξmax，当两侧阻尼器对称安装时，最大解ξmax所对应的两侧阻尼器的最优阻尼系数也会相等；阻尼器的安装位置越远离导线两侧端部，系统的一阶阻尼比提升效果越明显。

(2) 与传统粘滞阻尼器、粘弹性阻尼器相比，NSD 可以在较小的阻尼系数时显著地提高系统各阶阻尼比，且存在一个最优负刚度kopt使得系统一阶阻尼比可以达到最大。此外，NSD 能够明显降低导线系统的自振频率；NSD 安装位置的改变对系统的一阶最大阻尼比影响有限。

(3) 阻尼器的布置形式宜选择两侧对称布置，在满足阻尼器实际安装技术工艺、线路安全、电气绝缘要求的前提下，其安装位置尽可能远离导线两端；建议NSD 的刚度系数小于 |0.9kopt|，根据所选择的阻尼器刚度，阻尼系数选择系统一阶最大阻尼比所对应的最优阻尼系数Copt-1。

(4) 有限元仿真模拟表明，采用基于NSD 的防舞方案相较于传统粘滞阻尼器具有更好的防舞效果。