以结构反应均值估计为目标的时程分析输入地震波选择研究

张 锐，王东升，孙治国，李宏男，刘文锋

(1. 大连交通大学土木工程学院，辽宁，大连 116028；2. 中国地震局工程力学研究所，地震工程与工程振动重点实验室，黑龙江，哈尔滨 150080；3. 辽宁省隧道工程及灾害防控技术创新中心，辽宁，大连 116028；4. 河北工业大学土木与交通学院，天津 300401；5. 防灾科技学院土木工程学院，北京 101601；6. 大连理工大学建设工程学部，辽宁，大连 116024；7. 青岛理工大学土木工程学院，山东，青岛 266033)

时程分析方法已广泛应用于结构抗震设计及性能评估[1]，其结果受到诸多因素的影响，例如结构材料特性、场地条件、分析模型假定以及单元特性等。在诸多因素中，地震动输入是导致结构分析结果不确定性的最重要的影响因素[2−7]。虽然不同地震中获得的地震波存在天然的离散性，但在抗震认知累积基础上通过合理的选择和调整，可以实现对结构反应的“准确、有效、一致”估计[8]，既能够保证与结构真实反应具有较小偏差，又能够使结构反应结果的离散性在合理的范围之内。

时程分析通常采用具有统计特征的参数(如结构反应的均值、离散性、倒塌概率等)来描述结构的需求特征(或反应值)，当将所选的地震波逐条输入结构进行时程分析时，这是一项统计工作。由地震波数据库中选取某条地震波作为输入的过程相当于统计的抽样，那么抽取的样本(即选取的地震波)应该尽量与描述地震动的参数具备统计一致性。从工程地震学角度，地震动输入通常由各类“谱”来描述，如一致概率谱(UHS)[9−10]、条件均值谱(CMS)[11]、条件谱(CS)[12]等，皆反映了地震动的统计特征，这些统计特征可基于大量的地震波通过衰减关系获得。对于上述工作，作为抽样环节的地震波选取就架起了地震动输入与结构反应二者统计特征的桥梁(图1)。寻求到既具有地震动统计特征，又能够以少量的地震波计算结构的需求特征，这正是时程分析选波研究的价值所在。

图1 地震波选择是联系地震动输入和结构反应的桥梁Fig. 1 Ground motions selection is a bridge between records input and structural responses

目前，以特定含义下的反应谱作为目标谱，选取自身反应谱与目标谱“一致”的输入地震波，已成为最常采用的选波方法[13]。针对目标谱选择，规范设计谱[14]最为常用，也有学者提出一致概率谱(UHS)[9−10]和条件均值谱(CMS)[11,15−16]作为目标谱。这些目标谱均是加速度反应谱，更多地反映了峰值加速度(PGA)或加速度反应谱(Sa)的地震衰减或统计特征，其对于短周期或中短周期结构具有较好的反应相关性。而对于中长周期或长周期结构，速度谱、位移谱则可能更有优势[13,17−19]。针对谱匹配的计算，多数方法在计算地震波反应谱与目标谱的匹配误差时，通常不会对各阶振型周期的贡献区别对待，即对各个振型周期均赋予相同的权重。事实上，结构各阶振型对于地震反应的贡献是不同的，通常第1 阶振型贡献最大。虽然一些研究中考虑了不同周期范围取不同的加权系数[20−21]，但如何选择加权系数以及考虑加权系数后谱匹配选波对结构反应的影响，研究尚不足。此外，目前选波研究对于必须进行时程分析的减隔震结构，其适用性如何仍未开展充分研究。

工程师通常以结构反应均值作为抗震设计和决策的依据，因此本文以计算结构均值反应为目标，对时程分析选波方法开展了系统性梳理。针对目标谱法中的谱匹配调幅和目标谱选择两个方面，均提出了诸多较为可行的方法和意见，并进行了扩展性的讨论，旨在为包括耗能减震结构在内的以反应均值估计为目标的时程分析选波工作，提供切实可行的指导，并推动选波研究的深入开展和工程应用。

1 考虑多振型影响的谱匹配选波方法

如何通过(线性)调幅实现所选地震波反应谱与目标谱的一致，即谱匹配，是一个非常重要的问题。为考虑高阶振型对结构反应的不同贡献，作者们先后提出了两种考虑权重的调幅法，即双指标多频段工程经验方法[22− 24]和最小二乘加权调幅法[25− 26]。

1.1 双指标多频段工程经验选波法

1.1.1 方法简介

2000 年杨溥等[27]提出了双指标选波方法，由于其不仅考虑了结构基本周期T1邻域段，更考虑到反应谱平台段谱匹配的重要性，从而获得了良好的选波和时程分析效果。但考虑到近年来我国超高层建筑、大跨度桥梁和高耸电视塔等迅猛发展，这些结构往往基本周期较长(T1接近6 s～10 s及以上)。对这些长周期结构反应起重要作用的T2、T3等周期段很有可能并未落入平台段，采用该方法有可能会忽略这些高阶振型的贡献。因此，作者改进并提出了双指标多频段工程经验选波方法。

双指标多频段工程经验选波方法仍取用两个匹配误差指标作为选波的依据，选取两指标值均较小的地震波：一个与杨溥方法[27]采用的平台段误差指标相同，平台段范围仍取 [0.1,Tg]，特征周期Tg可根据谱形定在平台段的拐点处；另一个指标取用结构前几阶周期附近多个频段范围内，单个地震波反应谱和目标谱的均值相对误差之和，每个周期Ti邻域的频段长度[Ti−ΔT1,Ti+ΔT2]中ΔT1与ΔT2仍采用杨溥方法的建议值，分别取0.2 s和0.5 s。为体现各阶振型对结构反应的不同贡献，采用了由归一化振型(质量)参与系数确定的权重系数 λi[22−24]，其具有明确的物理含义，也可由常用的工程抗震分析软件直接计算，易于工程实现。

在应用中可首先固定PGA，然后，以放大系数谱为目标谱进行误差计算。因为平台段误差指标的存在，该研究思路与王亚勇[28]的建议较为类似，后者又基于有效峰值加速度(EPA)进行了再调整，以使得多条波的平均谱与规范目标谱达成一致。

1.1.2 结构反应分析

以一个25 层钢筋混凝土框架-剪力墙结构为例(见图2)，7 度抗震设防(0.15g)，Ⅲ类场地。以抗震规范设计谱为目标谱，备选地震波为10 个台站20 条地震波(水平双向)[24]。选取了双误差指标最小的3 条地震波进行弹性时程分析。所得基底剪力与反应谱分析结果的相对误差均在±20%以内(见表1)，完全满足现行规范关于时程分析结果与反应谱分析结果统计一致性的要求。

图2 25 层框架-剪力墙结构标准层平面图Fig. 2 Standard floor plan of 25-story frame-shear wall structure

表1 所选3 条波与反应谱结果对比Table 1 Base shear of the three records and the response spectrum

以一个30 层的钢筋混凝土框架-剪力墙结构为例(图3)， 8 度抗震设防，II 类场地。仍以规范设计谱为目标谱和20 条地震波为备选波，进行了弹塑性时程分析。由增量动力分析获得的输入PGA 和最大层间位移角的关系曲线(图4)表明，采用该方法选取的3 条地震波所得PGA-层间位移角均值曲线与20 条地震波所得均值曲线非常相近。

图3 30 层框架-剪力墙结构标准层平面图Fig. 3 Standard floor plan of 30-story frame-shear wall structure

图4 所选3 条波均值与IDA 均值比较Fig. 4 Comparison of the mean values between IDA and the three records selected by the developed method

作者们在文献[24]中以美国联合钢结构计划(SAC Steel Project)提出的9 层和20 层抗弯钢框架为例，先后进行了弹性和弹塑性时程分析。此次研究中目标谱取用了上述20 条地震波的均值放大系数谱，并以这20 条地震波产生结构反应均值作为目标反应(即“真实”反应)。研究表明：该方法选择的3 条地震波的结构基底剪力均值与20 条地震波的均值基本一致；结构最大层间位移角沿楼层的分布规律，以及对薄弱层位置的判断均与目标反应较为一致，相对误差在−20%～30%范围内。

综合上述算例分析表明，双指标多频段工程经验方法可以较为合理地考虑高阶振型对结构反应的影响，对高层钢筋混凝土结构和高层抗弯钢框架结构的地震反应均值估计，均具有较高的准确性，对于弹性和弹塑性时程分析均适用。由于该方法并不具备可靠的理论依据，因此认为是工程经验化的方法。

1.2 最小二乘加权调幅选波法

1.2.1 方法简介

基于最小二乘法确定的误差平方和形式的输入地震波反应谱和目标谱的差异，是相对于均值误差指标(即1.1 节中双指标多频段方法所用)更为科学的评判指标，其具有数学理论上的完备性，因此提出了最小二乘加权调幅选波法(简称加权调幅法)[25− 26]。

设定一个较宽的匹配周期范围(如0.2T1～1.5T1或2.0T1)，将其划分为多个周期段，每个周期段涵盖结构各阶周期点，并赋予与双指标多频段方法相同的权重系数 λi。误差指标SSEW和调幅系数SF可见式(1)和式(2)。

式中：Sa(Ti)和Sta(Ti) 分别是周期Ti处的备选波加速度反应谱和目标谱；m为匹配周期段内周期点数[11]； α 和 β是结构相邻两阶自振周期之间的权重系数分配的比例范围，满足 α+β=1即可，他们的取值对最终选波的结果影响很小[25−26]。

对于加权调幅法，权重系数的引入不仅可以起到考虑高阶振型影响的作用，最新研究表明，它还可以弥补算术坐标下SF主要由短周期谱值控制的不足，这点可以利用高维向量理论来解释[29−30]。说明一点，加权调幅法中的反应谱也同样可以采用放大系数谱，优选出地震波后可再依据PGA 进行调幅，这样可实现与我国抗震规范要求的统一。

1.2.2 结构反应分析

以15 层(图5)和上述30 层(图3)钢筋混凝土框架-剪力墙结构以及44 层钢筋混凝土框架-筒体结构(图6)为例，它们均位于8 度地震烈度区(0.2g)、II 类场地。模型详细信息也可参考文献[31]。

图5 15 层框架-剪力墙结构标准层平面图Fig. 5 Standard floor plan of a 15-story frame-shear wall structure

图6 44 层框架-核心筒结构标准层平面图Fig. 6 Standard floor plan of a 44-story frame-core tube structure

1)目标谱的影响研究

以抗震规范设计谱和区划图反应谱[32− 33]为目标谱，分别采用加权和等权方法(即权重系数取1.0)对结构的最大层间位移角的均值和变异系数(COV)进行了对比(见图7 和图8)。因44 层结构周期较长(T1= 4.23 s)，目标谱的长周期无法确定至1.5T1(即大于规范设计谱上限6.0 s) ，因此，采用了谱值水平延拓的方法，即将6.0 s 之后的谱值均取6.0 s 处的谱值。考虑8 度罕遇地震作用，基于SUSAGE 软件进行时程分析，备选地震波取20 个台站40 条地震波(水平双向)[25−26]。选取由式(1)计算的误差指标SSEW最小的7 条地震波作为时程分析输入。

由图7 可见，44 层结构采用以抗震规范设计谱为目标谱的加权调幅法所得最大层间位移角明显较大，原因在于目标谱在长周期段的人为修正及水平延拓，使谱值出现了明显的失真。除此之外，其他情况下所得最大层间位移角均比较相近，相对误差均在±10%以内。在降低结构反应离散性方面，由图8 可见，对于这两种目标谱，加权方法的COV 均低于等权方法，尤其对于长周期结构(如44 层)，加权方法可使COV 降低至等权方法的50%左右。这证明了加权调幅法在降低结构反应离散性方面较等权方法存在明显优势。

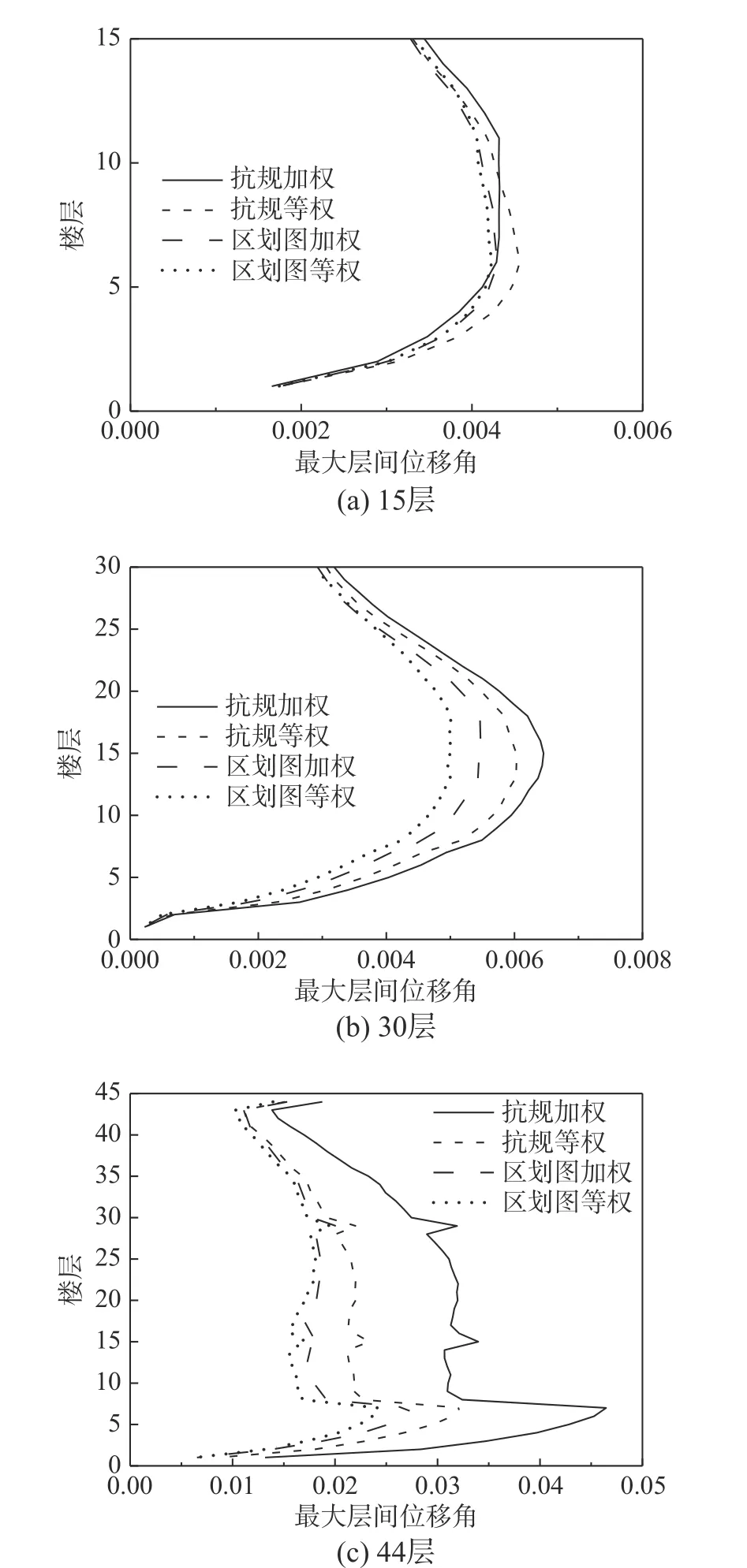
图7 加权与等权方法基于两种目标谱时最大层间位移角均值Fig. 7 The mean of peak inter-story drift ratios by the weighted and unweighted scaling methods using two target spectra

图8 加权与等权方法基于两种目标谱时最大层间位移角COVFig. 8 The COVs of peak inter-story drift ratios by the weighted and unweighted scaling methods using two target spectra

2)天然波与人工波的比较

以上选波研究中，备选波均出自天然强震记录数据库。基于小波算法确定的人工波的反应谱可以在匹配周期范围内实现与目标谱的良好匹配，因此目前被公认为是估计结构反应均值效果最好的地震波，美国规范ASCE7-16 也明确地将基于小波算法取得的人工波作为备选地震波。但人工波也存在一定弊端，如其反应谱在超出匹配周期范围时会出现明显的畸变以及无法表征脉冲效应等。以台湾集集地震的地震波TCU042-W[25]为例，图9 中原始波经幅频调整后，在匹配周期以外(4.5 s 之后)出现了明显的偏移。因此，有必要将基于天然波选波的加权调幅法与基于小波算法生成的人工波方法进行比较，从而更为客观地评判加权调幅法在估计结构反应均值方面的准确性。

图9 调幅后人工波与目标谱的匹配(TCU042-W 为例)Fig. 9 Spectral matching between the scaled artificial wave and target spectrum

以8 度地震烈度区(0.2g)罕遇地震作用的抗震规范设计谱为目标谱，将加权调幅法[25− 26]选择的天然波与基于小波算法[34]开发的SeismoMatch程序生成的人工波输入下(各7 条)，结构时程分析结果进行比较。在这部分比较中还另外考虑了冀昆等[14]建议的与8 度地震烈度区(0.2g)罕遇地震作用的抗震规范设计谱具备完全匹配的7 条天然波作为输入。

图10 和图11 给出了前述结构的最大层间位移角均值和COV 沿楼层的分布情况。由最大层间位移角均值可见，对于15 层和30 层钢筋混凝土结构，人工波方法和冀昆方法比较相近且稍大于加权调幅法；但当建筑高达44 层时，虽然3 种方法选取的地震动记录并不相同，但他们所得最大层间位移角均值沿各楼层却非常地一致。由此可见，天然波和人工波方法所得结果较为一致，尤其对于长周期结构，加权调幅法和冀昆建议的地震波在估计结构反应均值方面均具有较高的准确性。由最大层间位移角COV 对比可见，加权调幅法和人工波方法所得3 个结构的COV 值均较相近，且均明显小于冀昆方法。可见，加权调幅法和人工波方法在降低结构反应离散性方面均较有优势，加权调幅法在估计结构反应均值方面离散性仍然较低。

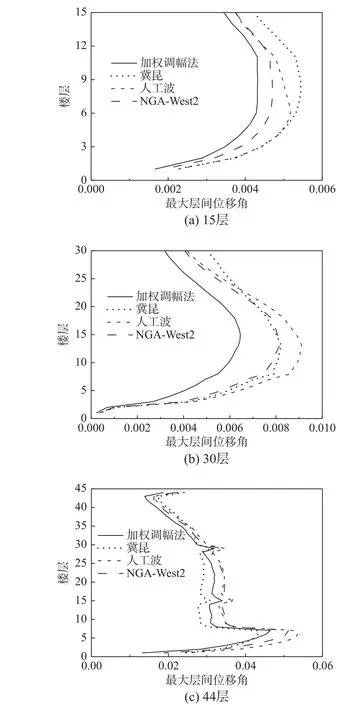
图10 天然波与人工波方法所得最大层间位移角均值Fig. 10 The mean of peak inter-story drift ratios by the methods that apply to real earthquake records and artificial waves

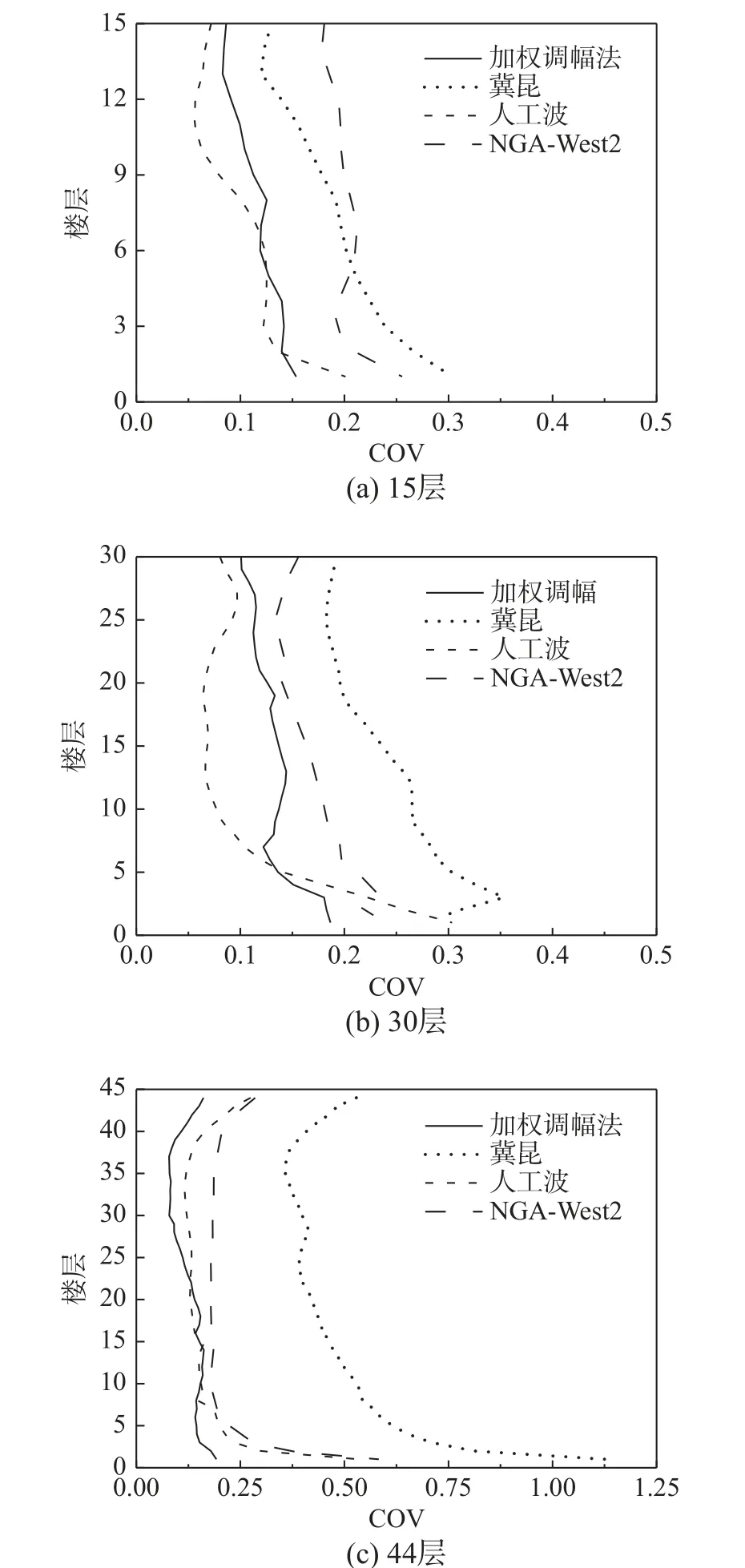
图11 天然波与人工波方法所得最大层间位移角COVFig. 11 The COVs of peak inter-story drift ratios by the methods that apply to real earthquake records and artificial waves

3)备选波数据库容量的影响

1.2.1 节中提到的加权调幅选波方法的研究是在40 条小型备选波数据库中完成的，样本(地震波)容量的大小是否会影响选波研究的效果也是一个值得关注的问题。本节将NGA-West2 强震数据库中的选波工具模块引入，并与加权调幅法、冀昆方法和人工波方法等的结构时程分析结果进行对比。

利用NGA-West2 强震数据库网站(https://nga west2.berkeley.edu/)可自定义目标谱及选波限制条件等，其匹配误差是基于最小二乘法进行计算的。因为该数据库的选波模块是在对数坐标下完成，作者在文献[29 − 30]中已经指出算术和对数坐标下谱匹配选波的不同，后者会更多兼顾长周期段的贡献，而前者则必须要考虑权重系数(即本文的加权调幅法)。因此，基于该数据库在对数坐标下选波，权重系数的作用是有限的。

仍以我国8 度地震烈度区(0.2g)罕遇地震作用的抗震规范设计谱为目标谱，基于NGA-West2强震数据库优选21 条地震波输入所得结构时程反应也一并示于图10 和11。由图可见，几种方法所得最大层间位移角均值没有明显差别，大样本容量所得结构反应会稍大于小样本容量，且与人工波方法非常相近。由COV 的对比关系也同样说明本文关于加权调幅法研究的结论是具备一般性的。

4)输入地震波数量的影响

为进一步探讨地震波数量对选波研究的影响，本节将基于NGA-West2 数据库优选的21 条地震波随机等分成3 组(每组7 条波)，将21 条地震波组与7 条地震波的3 个随机组以及加权调幅法(7 条波)和冀昆方法(7 条波)所得最大层间位移角进行对比。由于人工波方法是公认的估计结构反应均值效果最好的地震波，因此，以人工波方法所得最大层间位移角均值为基准(图10)，将上述几种分组所得最大层间位移角均值相对于人工波方法的相对误差进行对比，如图12。

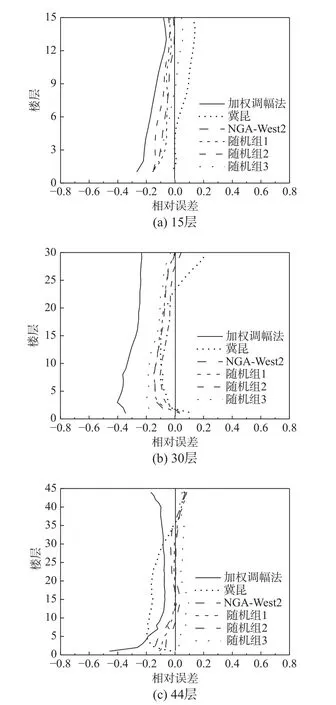
图12 各数量分组所得最大层间位移角的相对误差Fig. 12 The relative errors of peak inter-story drift ratios of these groups including different number records

由图可见，NGA-West2 方法(21 条波)与人工波方法(7 条波)的最大层间位移角均值非常接近，3 个结构的相对误差均在±20%以内，尤其对于44 层结构，两者结果沿各楼层均非常一致。再对比3 个随机组，它们的相对误差也均可控制在±20%以内。加权调幅法与冀昆方法的相对误差较NGA-West2 方法稍大，但冀昆方法的相对误差总体仍可控制在±20%以内，加权调幅法的相对误差也仅是在30 层结构的下部楼层(10 层以下)较大，约在30%～40%。总体来说，选取7 条地震波的各个分组与21 条地震波组的结果均较为接近，且相对误差也可控制在合理范围内，因此，认为7 条是时程分析选波较为合理的地震波数量。

2 减隔震结构选波方法的适用性

现有选波方法大多针对普通的底部固端结构(即非隔震结构)，对于减隔震建筑的地震动输入问题仍鲜有研究[20,26,35]。由于减隔震建筑中的隔震器件在强震中会产生塑性反应，对此类结构进行抗震设计必然要进行时程分析。因此，关于减隔震结构时程分析的地震波选择问题很有必要开展研究。

以某4 层和5 层的隔震结构为例(图13 和图14)，仍考虑8 度罕遇地震作用(0.2g)，Ⅱ类场地。采用加权调幅法与冀昆方法和人工波方法进行地震波选择，对结构反应以及隔震支座反应进行对比分析，如图15～图17 所示。

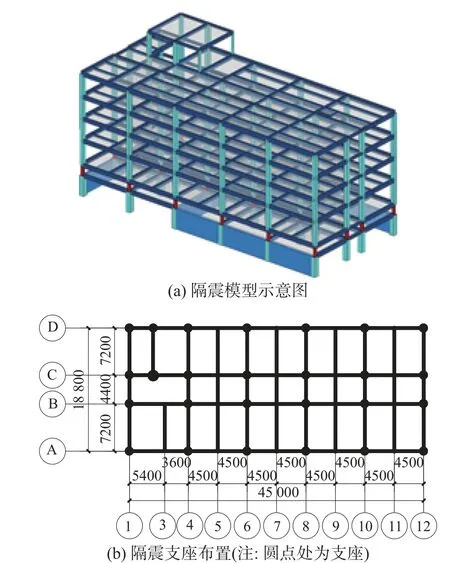
图13 4 层隔震结构模型与支座布置Fig. 13 4-story isolation structure and isolation bearing

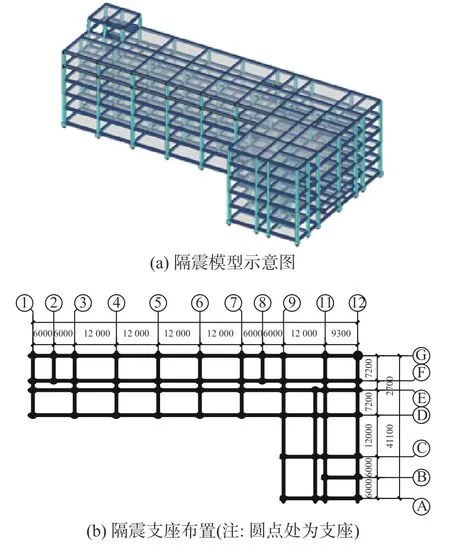
图14 5 层隔震结构模型与支座布置Fig. 14 5-story isolation structure and isolation bearing

图15 隔震结构最大层间位移角均值Fig. 15 The mean of peak inter-story drift ratios

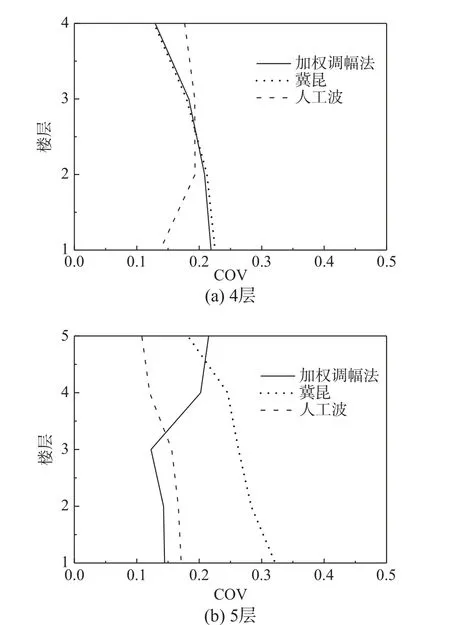
图16 隔震结构最大层间位移角COVFig. 16 The COVs of peak inter-story drift ratios

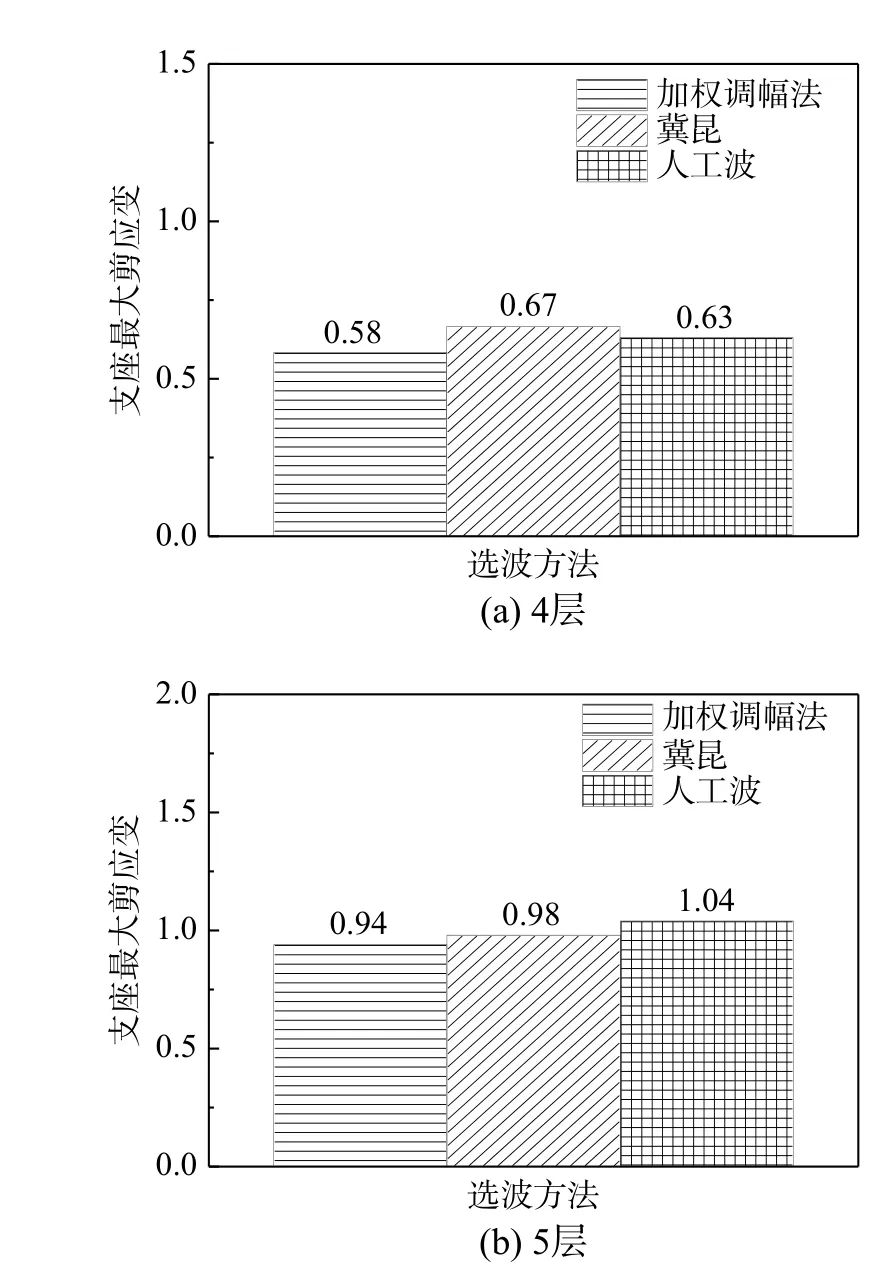
图17 隔震支座最大变形Fig. 17 The maximum responses of isolation bearings

研究表明，3 种方法所得上部结构最大层间位移角均值沿楼层的分布规律基本一致，但对薄弱层位置的估计有所不同，最大值之间仍有6%～52%的差距；3 种方法所得隔震层支座的最大反应均值相差不大，相对误差在13%～29%。就本文算例来看，加权调幅法在减隔震结构的时程分析中也具有可行性，但目前的适用性研究尚处于起步阶段，仍需深入开展。

3 以Newmark 三联谱为目标谱的讨论

目前选波研究中常用的目标谱多为加速度反应谱(上述选波方法均为加速度目标谱)，它们对于短周期和中短周期结构反应具有较好的相关性，而对于中长周期和长周期结构优势不足。因此，提出了将Newmark 三联谱作为目标谱的选波方法[36]。由NEWMARK 和HALL[37]于20 世纪60 年代提出的Newmark 三联谱是基于峰值加速度(PGA)、峰值速度(PGV)、峰值位移(PGD)建立的放大系数谱，其理论基础源于拟加速度反应谱PSa、拟速度反应谱PSv和位移谱Sd，满足PSa=ωPSv=ω2Sd的关系，其计算出发点是位移谱Sd(T)。Newmark三联谱的一个重要特点，即“长周期处满足结构反应的物理条件：位移反应趋近于PGD”，相较于常用的加速度反应谱，Newmark 三联谱对于长周期结构反应的相关性尤为密切。

3.1 目标谱的构建

将SAC 计划提出的代表3 种超越概率水准(即50 年超越概率50%、10%和2%)的3 组各20 条地震波的2%阻尼比的拟速度反应谱平滑成Newmark三联谱，再取均值，设为目标谱(图18)。不同阻尼比的拟速度谱统计得出的均值Newmark 三联谱即可代表不同阻尼比下的目标谱。

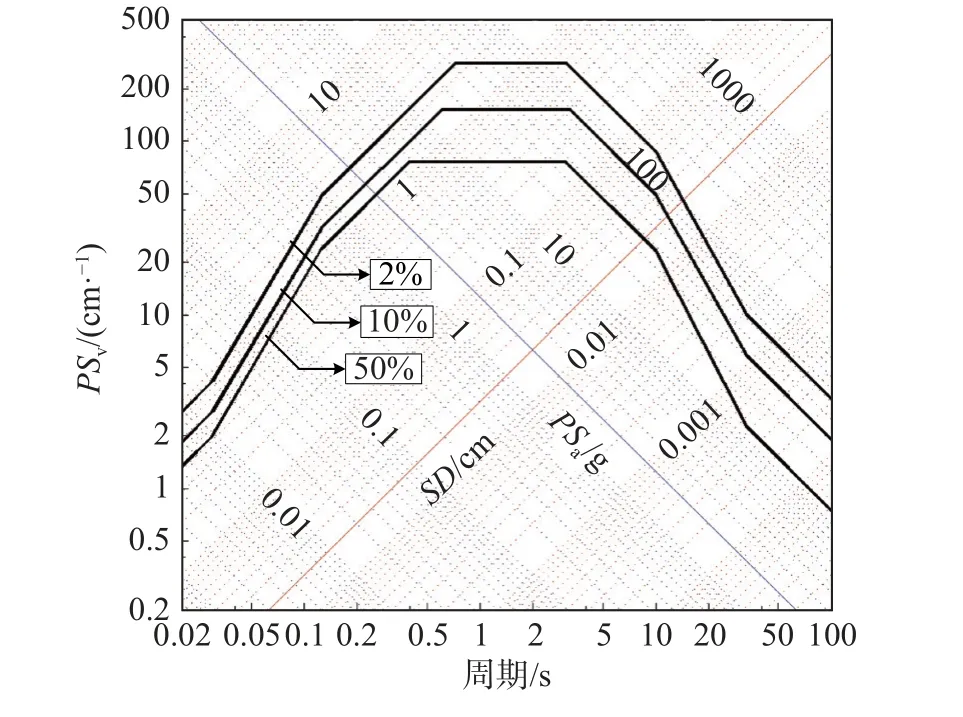
图18 Newmark 三联谱确定的目标谱(阻尼比0.02)Fig. 18 Target Newmark spectra at the three hazard levels,ξ=0.02

采用最小二乘法计算匹配误差SSEN和调幅系数SF。由于Newmark 三联谱具有加速度、速度和位移3 个敏感段，匹配误差计算应分别用各敏感段的加速度、速度和位移谱值进行计算。但考虑到周期拐点位置不易确定，因此，利用PSa=ωPSv=ω2Sd关系，在3 个敏感段均采用拟速度谱形式计算匹配误差SSEN和调幅系数SF(式(3)和式(4))。

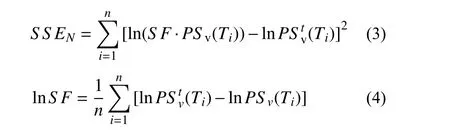
式中，PSv(Ti)和PStv(Ti)均是经平滑标定后的Newmark 三联谱形式的拟速度谱。

3.2 结构反应分析

仍以SAC 计划中提出的9 层和20 层的钢框架为例[24]，目标反应与备选地震波均同上述加权调幅法。以Newmark 三联谱为目标谱方法和以常用加速度反应谱为目标谱方法(即将式(3)和式(4)中的拟速度谱PSv换成加速度谱Sa，同样采用对数坐标计算匹配误差和调幅系数)所优选出7 条地震波得到的最大层间位移角均值和COV 进行对比(如图19 和图20)。研究表明：两种方法对结构反应均值的估计相差不大，当结构非线性程度较高时，Newmark 三联谱方法所得结构反应稍小；从最大层间位移角COV 对比可见，两种方法所得结构反应的离散性均较小，但当结构周期较长时(如20 层结构)，Newmark 三联谱方法在底部薄弱层附近的COV 更大一些。

图19 两种目标谱方法所得最大层间位移角均值Fig. 19 The mean of peak inter-story drift ratio demands by both target spectrum methods

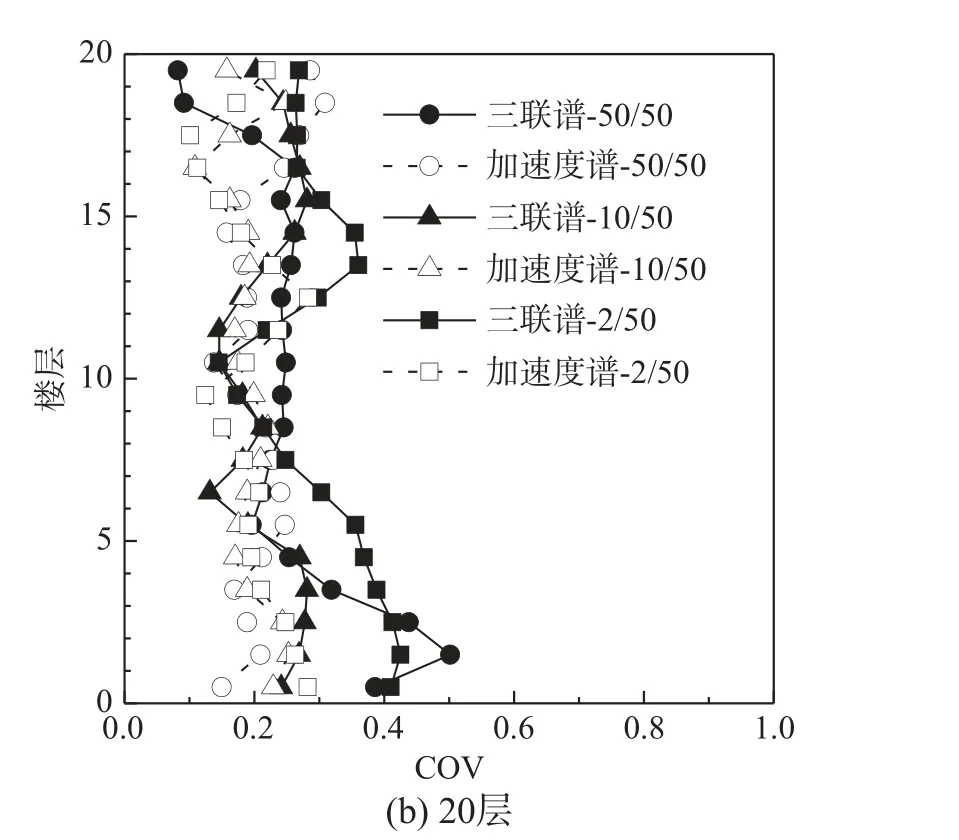
图20 两种目标谱方法所得最大层间位移角COVFig. 20 The COVs of peak inter-story drift ratios by both target spectrum methods

从目前的分析结果来看，以Newmark 三联谱为目标谱的方法对于结构反应均值估计的准确性较为可靠，但所得结构反应离散性仍较传统加速度目标谱方法偏大。Newmark 三联谱对于长周期结构反应的良好相关性并没有突显出来，对于以Newmark 三联谱为目标谱的选波方法，仍需开展更为深入的理论探究。

4 结论

本文针对以结构反应均值估计为目标的时程分析选波问题，基于目标谱法，在谱匹配调幅和目标谱选择两方面均进行了系统深入的研究。对提出的双指标多频段工程经验选波法和理论更加完备的最小二乘加权调幅法，进行了详尽的算例分析。将加权调幅法与国内学者、人工波方法以及NGA-West2 强震数据库选波模块方法进行了比较分析，并探讨了加权调幅法在减隔震结构中的适用性。目前已获得的主要成果及认识如下：

(1) 以归一化振型参与系数作为权重系数，改进及提出考虑高振型影响的双指标多频段选波方法，是一种半工程经验的方法，对结构弹性及弹塑性时程分析选波均具有可行性，能够满足现有抗震规范的要求。

(2) 加权调幅法与国内学者、人工波方法以及NGA-West2 强震数据库选波模块方法的比较研究表明，加权调幅法在估计结构反应均值方面具有可靠的准确性，并进一步明确了其优势在于可明显降低结构反应的离散性。这种优势也不会受到目标谱选择的影响。

(3) 加权调幅法已初步用于减隔震结构的时程分析，现有算例分析表明，该方法具有一定的适用性。

除谱匹配研究外，本文还建议以Newmark 三联谱作为目标谱，拟解决长周期及超长周期结构时程分析输入地震波选择问题。如上的认知均是以结构反应均值估计为目的，但随着基于性能的抗震设计理念的深入，地震危险性概率方法的逐渐完善，结构反应的概率分布也成为设计者们需要预测的反应指标。因此，在匹配目标谱均值的同时也应兼顾目标谱的方差匹配，关于此项研究尚待开展。