基于单体视觉投影的集群控制策略

张 胜，胡学峰，刘 畅，李 娟

（1.安徽军工集团控股有限公司，合肥 230051；2.北京理工大学机电学院，北京100081）

1 引 言

近年来，随着计算机技术、大数据、人工智能、集成电路等领域的不断发展与突破，无人系统技术得到了迅猛发展[1]。受单一平台的能力约束，无人系统集群技术作为第三次抵消战略的五大支撑技术之一，得到各国高度青睐[2-3]。对集群行为的研究最初起源于人们对自然界众多生物集群行为的好奇和探索。20世纪50年代初期，学者 Grasse[4]通过对社会性昆虫的行为进行研究观察到：单个个体行为较为单一，其能力也十分有限；然而由大量昆虫组成的集群则能表现出强大的能力, 能够完成各种复杂高难度任务。大量简单个体通过有序组合所表现出来的集群能力称之为“群体智能（Swarm Intelligence, SI）”。

近年来，作为无人系统集群研究领域的关键问题之一，集群控制受到了大量学者的关注。现有无人系统集群控制策略主要沿以下两条思路进行。（1）根据任务需求将群体任务进行分解，通过个体间通信和协调完成特定队形的保持和动态调整。合理的编队飞行可以提高任务完成效率，抵御外来入侵，增加集群灵活性，进而保证系统稳定性。（2）从仿生学的角度出发，研究自然界中社会性群落的集群行为，分析其中原理机制，借鉴生物集群的主要思想，设计适用于无人系统集群的控制策略。以下分别针对这两类研究思路进行相关文献概述。

基于个体间协同的无人平台编队方法是当前集群协同的主流方法之一。关于此种无人机编队控制方法已经发展出了几种主流思想[5-7]。（1）基于行为法。通过定义和设计基本行为，如跟随、避障、队形变换等，进行集群控制。Balch等[8]开创性地提出将基于行为的编队控制方法用于机器人编队控制。基于行为法可以综合队形中其他个体的运动状况，产生自身的运动决策，以保持整体队形的稳定性。然而，此控制方法主要通过预设信息和各种触发条件来产生自身控制指令，不能明确地定义群体行为，在数学上对其行为进行分析和仿真的难度较大，保持队形稳定的耗费较大，编队的适应性和灵活性也因此降低。（2）领航控制。集群中个体在遵守自身运动规则的前提下，令集群中的少数个体拥有更多的环境信息和运动信息，赋予其更强的信息处理能力和交互能力[10]。通过领航个体与其他个体的局部通信交换运动位置信息，最终实现群体按照特定队形和方向运动。领航跟随算法是目前编队控制最常用的方法之一，具备较强的扩展性，然而可能存在系统中队形反馈不明确、领航者失效等问题。（3）虚拟结构法。将编队整体设想为一个物理上的刚体，依据集群系统的几何中心或队内虚拟或真实的长机标定个体的相对位置[9]。虚拟结构法避免了传统领航编队方法中领航无人机出现故障或失去功能时编队无法继续保持的缺点，并且可以很容易地指定机器人群体的行为并及时得到队形反馈，能够取得较高精度的轨迹跟踪效果。然而，计算合成虚拟长机和获取邻机位置，需要较高的通信质量和较强的计算能力。（4）人工势场法。通过势函数对集群系统中的局部行为规则以及环境对单一个体的作用进行描述。每个个体在势函数的约束下进行行为选择[11]。然而，此类方法存在势函数设计难等缺陷。除了上述几种典型的集群编队控制方法外，学者们还发展出图论法、一致性法以及各类混合控制法，满足了集群面对复杂环境的任务需求，增强了系统鲁棒性。

无人系统的集群控制与生物群体智能行为较为相似[12]。换句话说，实现无人系统集群控制的一条重要思路是对自然界生物群体智能行为进行原理性探究。Reynolds[13]建立了一种模拟智能体的Boids模型，用于模拟鸟类等动物的群体运动。这些智能体不受任何中央控制，只依赖于每个智能体的个体行为和其局部的互动。互动由3个基本操作构成：聚集、分离以及对齐。匈牙利物理学家Vicsek等[14]从统计力学的角度提出了Vicsek模型，通过对集群密度与噪声强度等参数的修改，对受生物启发建立的数学模型进行了定量分析。Vicsek模型在自主控制机器人与分布式传感器网络中有着广泛的应用。Spector等[15]在Boids模型的基础上，对个体行为进行量化分析，并结合Reynolds基本规则，建立了Swarm模型。Kwong等[16]在此基础上采用启发式算法对模型的参数与集群行为涌现模式进行了研究。Wu等[17]在Swarm模型基础上，引入了粒度的概念并建立了基于粒度的Swarm模型（Granular-Swarm模型），根据不同的粒度对该模型的涌现行为进行了研究。Jadbabaie等[18]针对 Vicsek模型非线性部分求解与分析困难的问题，对Vicsek模型进行了线性化。Cucker等[19]在 Vicsek模型基础上，建立了所有个体速度方向均不相同的数学模型，并利用图论中的连通性理论对模型所产生的集群涌现行为进行了分析，对涌现行为与模型参数之间的相互关系进行了证明。 Duna等[20]提出基于鸽群行为机制的多无人机自主编队方法。Pearce等[21]提出了一种利用投影方式来模拟鸟群中信息传递的数学模型，该模型通过少量参数来控制鸟群的密度，进而模拟多种鸟群的飞行行为。姜龙亭等[22]针对集群执行任务时的个体之间的防碰撞问题，提出了基于群智机理的集群防碰撞控制方法，提高了集群的集结效率。Charlesworth等[23]提出了一种基于未来状态最大化原则的鸟群运动模型，尽管没有明确设定聚集、散开、避碰等规则，但鸟群在运动中仍涌现出了这些行为。这一研究为揭示生物集群行为内在机理提供了一种新的思路。

综上所述，现有集群控制策略大多采用基于上层规划的方式，需要人为设定明确的行为规则供无人系统集群使用或遵守。这类方法的智能程度较低，可扩展性及环境适应性较差。当遇到未预先定义的场景或状态时，无人系统则难以做出适当的行为，以有效应对出现的意外。此外，现有研究大多依赖于无人系统之间的双向信息交互。当无人系统之间的通信受到环境或敌方干扰而无法正常工作时，集群协同效能将受到极大的影响。本文从仿生角度出发，建立基于单体视觉投影的集群控制模型，实现大规模集群行为自组织涌现。此外，设计避障机制实现对入侵者的检测和规避，探究集群队形的变化特性。

2 单体视觉投影的自组织集群模型

生物学家的研究表明：鸟群仅依靠视觉信息输入便能够保持自身与群体其他个体的相对位置关系，进而保持整个群体队形的有序性。在生物集群运动过程中，绝大多数的单体因其移动速度快、距离远，很难被追踪到，甚至在整个群体中很难被辨别出来。一个在天空中飞行或海洋中游泳的鸟群或鱼群结合其活动背景会体现出强烈的视觉反差，将集群中的单体看成视域中快速移动的黑影，将天空看成较为单一的光背景，这就形成了类似于鸟类视网膜中的投影，称作视觉投影模型[22]。图1展示了其他单体在一个单体视网中的投影情况。其中，黑色圆盘代表个体agenti(i= 1 ,2,…,N)及其视觉感知邻域中的友方个体，N表示集群规模，θij(i= 1,2,… ,N;j= 1 ,2,…,11)代表邻域个体在个体agenti邻域中的视觉投影角度信息。

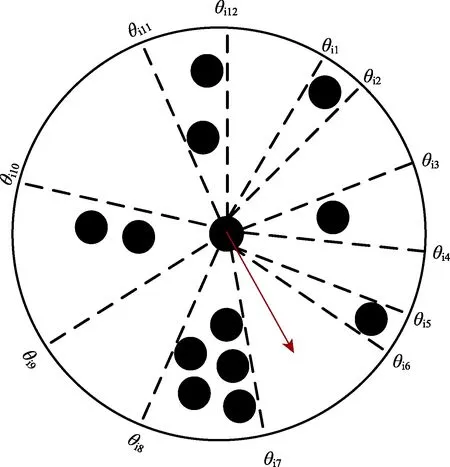
图1 单体视觉投影示意图Fig.1 Illustration of vision projection

基于上述视觉投影输入信息，个体agenti的速度和位置的更新方程为

2.1 投影项（Projection）

每个个体通过视觉感知可获得其感知范围（即感知邻域）内个体的方位角信息θij(i= 1 ,2,…,k= 1 ,2,… ,N}为个体agenti的感知邻域集合，d(xi,xk)表示agenti和agentk之间的距离，r为感知半径，|·|表示集合的势。为了便于后续进行计算，在指定的坐标系下，通过下式将θij限制在区间[0 °,360°]内。

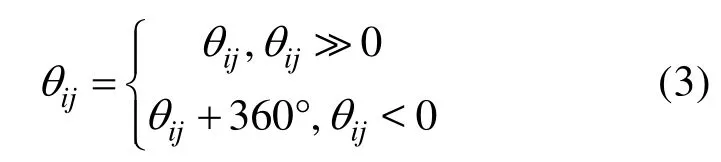
综上，邻域投影个体的方位角信息对每个个体带来的投影项可描述为

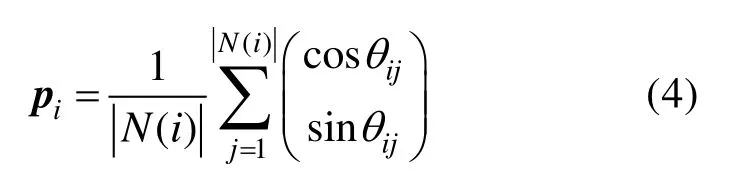
投影项对应于动物集群中单体倾向于向黑影-光亮边界寻找最佳方向的行为。需要说明的是，该项中不仅包含了群体内个体的投影，当有集群外个体进入后也会产生投影，这类信息如何使用和集群的任务是紧密相关的。在第3节中将以避障为典型案例阐述当其他个体运动信息被探测到后个体当如何反应。另外，这一模型也同样可扩展到三维的场景，二维平面的投影图也会变成一个球体域，投影项pi也会变为三维向量。

2.2 列队项（Alignment）

通过对感知邻域N(i)中个体速度朝向信息的获取，形成最近邻居个体速度的平均值，即列队项

列队项保证每个个体与其感知到的其他个体的速度方向保持匹配，如此便能将产生集群列队飞行的集群行为。

2.3 噪声项（Noise）

最后，在每次单体坐标更新的迭代算法中加入了随机的扰动项ni，且每个步长所遭受的扰动量均不相同。噪声扰动的加入使得群体间的无序性增强，来自于对昆虫集群行为的成功模拟。噪声项的引入给集群带来的干扰，但是仍能保持良好的聚集性。

3 基于单体视觉投影的避障模型

在自然界中，社会性群居生物必须具备抵御入侵者（捕食者）干扰（攻击）的能力，才能给予群体中个体足够的保护。每个个体有序且快速地躲避入侵者，对于在冲突中减少群体损失起到重要作用。入侵避障功能要求入侵者向群体中某个位置或某个个体任意时刻发起攻击时，处在集群中的每个个体要在入侵者进入到自己的感知范围内时能及时做出正确的响应，且响应必须保证自己和群体的安全。

通过设计一个朝向质心的入侵者模型，使得群体队形受到较为强烈的扰动。具体地，假设入侵者以两倍群体运动速度从群体外任一点开始攻击，且始终朝向群体质心运动。入侵者速度和位置变化公式为

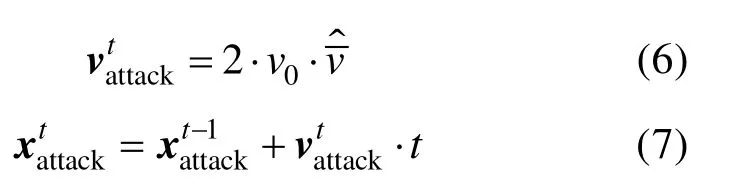
式中，表示群体质心速度的归一量，即群体质心速度方向。考虑到已有的群体内的投影图规则模型约束，通过设置每个个体的警戒范围rattack，使得rattack范围内的个体受到入侵者和投影图规则的双重影响而改变自身速度和位移，即个体速度转向与入侵者速度朝向垂直的方向以两倍于群体飞行速度进行逃逸；对于rattack范围外的个体，除了继续受单一的集群机制控制之外，还会根据附近是否有入侵者进行协调，可以通过公式进行调整

加入该项的影响过后，集群中单体速度和位置的更新公式变为

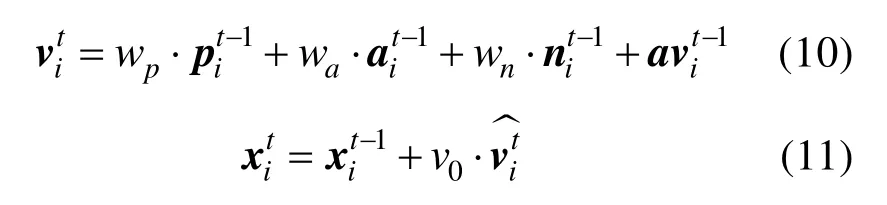
最终希望看到的效果是，入侵者撤退或穿出群体队形，并逐渐远离群体，离开每个个体的探测范围，群体重新处于安全状态，正常飞行。同时，群体内部逐渐恢复聚集。在后续的数值实验中，本文将探究不同的警戒范围、不同入侵者影响范围、不同个体探测距离对于群体行为的影响。

4 数值实验

4.1 算例及集群行为评价指标

（1）群体重心

为了直观地展现出群体的飞行轨迹和在飞行过程中的群体的有序性和队形保持的稳定性，给出群体重心C的计算公式为

式中，N为群体规模，xi为个体位置坐标。

（2）速度偏差相关度[23]

通过定义群体中个体间的速度（朝向）偏差以及相关程度，来反映群体间的协调性度量。

首先求出每个个体与群速度的偏差

式中，vi为agenti的速度；v表示群体质心速度，此处可以理解为群体速度的平均值；ui为个与群体的速度差。个体之间的速度偏差的相关函数C(d)定义为

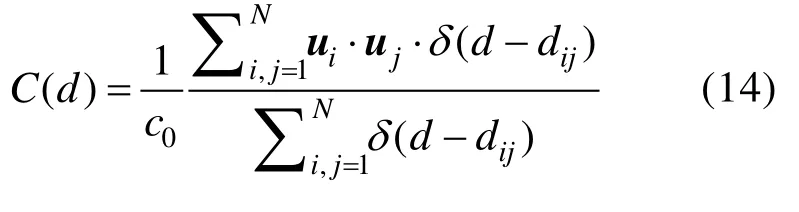
式中，N为群体规模，dij为两个个体之间的距离；d为距离阈值；δ(d-dij)为狄拉克函数；c0作为比例因子，本文将它定义为c0=1；C(d)衡量了在距离d时速度偏差的平均内积。较高的C(d)值表示在一定的距离内的所有成员之间的速度（朝向）具有很强的相关性，此时群体表现出高度一致的状态，即所有单体的飞行方向基本统一。

（3）群体极化函数[24]

群体的极化现象一般分为全局（Global Polarization）的极化和局部极化（Local Polarization）两个方面来考量[24]。此处考虑全局极化函数

式中，N为群体规模，vi为agenti的速度；v表示群体质心速度，此处可以理解为群体速度的平均值。群体极化函数Φ是基于单位向量的点积，其取值范围为 0~1。较大的Φ值意味着群体有更强的极化效果，群体更加有序。

4.2 不同类型集群行为

为了探究在不同参数(wp,wa,wn)组合下，自组织集群所表现出来的不同集群形态，本文设置了如表1所示的参数组合进行实验验证。wp代表投影图的权重；wa代表最近邻邻居的平均项权重，即群体一致性的重要权重；wn则表示施加在群体里的扰动，wn值越大，则群体的无序性相应加强。

表1 三组测试算例下的不同权重设置Table 1 Parameter settings for three test cases

在仿真过程中，设计不同的模块来分别表达速度的调整以及位置的调整，通过迭代进行输入的变换，进而实现位置、速度的更新。这里设置群体规模为100，迭代总步长为1000次，单体探测范围（邻居交互机制中的最大范围）为r=10。初始的个体位置坐标和速度朝向均为随机设置。

图2~4展示了3组权重下集群行为情况及相关指标随迭代步长的变化。群体运动全程的系统稳定性可以用群体质心的运动轨迹来进行考察，通过对每次迭代后的队形求质心坐标并记录，得到群体的质心运动结果。从图2可以看出，质心运动轨迹较为平滑，未出现明显的剧烈震荡，说明群体具有较高的稳定性，群体质心在按照群体决策稳定运动。此外，速度偏差相关度大多数情况为正，可见群体处于相对紧耦合的状态，群体间速度偏差不大，群体飞行过程中的协调性较高。最后，通过分析群体极化函数曲线可知，群体表现出先从松耦合到紧耦合约束然后再逐渐放松耦合程度的过程，即函数先增后减，并且此趋势具有一定的不规则的周期性。这一现象符合自然界动物集群的约束过程，即集群内部存在某种反馈机制，可以纠正某些速度与整个群体相差较大的个体的运动行为，从而达到群体的高度一致性。

图2 组合1集群行为示意图及相关指标Fig.2 Illustration of swarm behavior and related metrices for case 1

组合2的情形提高了投影项的权重，降低了列队项的权重，则群体将更多地依赖投影项进行控制，同时，噪声扰动项有所下降。在此权重规则组合的情况下，群体仍能保持很好的有序性和一致性，具体表现在较平滑的群体运动轨迹（群体质心轨迹），如图3所示。从图中可以看出，在经过大约200次迭代后，速度偏差相关度逐渐趋近于0，与组合1（图2）的速度偏差相关度函数变化趋势相差明显。这一现象可能由于群体间的扰动而有所减少。

图3 组合2集群行为示意图及相关指标Fig.3 Illustration of swarm behavior and related metrices for case 2

自然界中，昆虫类群体的主要表现为较高的无序性和混乱性，本模型可以很好地对昆虫的集群行为进行模拟。具体可以通过减小投影项权重，增加噪声项扰动实现，如图4所示。噪声项扰动的增加使得群体中的个体不再具有较高的一致性，个体速度方向呈现出多向化趋势。值得一提的是，在仿虫群的过程中，由于噪声项的引入，会随即发生群体中个体丢失的状况，这也是群体无序性的一个重要体现，表现在评价指标里则会出现群体质心严重波动的情形。与前面两组实验相比，组合3集群的速度相关性更加离散。同时，群体间形成的全局极化不够稳定，极化函数出现较为严重的波动。

图4 组合3集群行为示意图及相关指标Fig.4 Illustration of swarm behavior and related metrices for case 3

经过以上3组的仿真可以看出，在噪声项wn较低的水平下，wa项在群体中有着强制性矫正的作用。随着wa项的降低，在极化函数上则表现为上升过程的缓慢，群体一致性的演化过程变得缓慢，但是因为wp项的增加，使得群体间通过视网膜投影进行协调演化的规则得到增强，群体的极化程度在达到一定值后，能表现出更好的稳定性。

4.3 群体避障行为

基于4.2节的实验，考虑在组合2情形下探究存在外来入侵者情形下群体的避障行为。在此，设置集群中个体警戒范围为r=10，入侵者以两倍群体速度，即2v0，从原点出发追击运动过程中的集群。对于群体避障任务，该过程中会出现入侵者穿透集群和入侵者撤出集群两种情形。图5~6分别展示了两种情形下集群行为以及指标随迭代次数变化情况，图中红色个体代表集群中的个体，黑色个体代表入侵者。

从图5可以观察到，黑色入侵者朝向群体重心进行入侵，当其行为被最外围单体探测到后，群体由外到内依次做出响应。原本聚集的个体由于遭受入侵者的冲击，迅速散开，群体保持散开队形并与入侵者保持安全距离持续飞行。需要注意的是，这里很多内圈的个体并没有看到入侵者，而是被其他个体的行为所影响。

图5 入侵者穿透集群行为示意图及相关指标（入侵者预警范围 ra t tack = 1 0，个体的探测范围r=5）Fig.5 Illustration of swarm behavior and related metrices when the attacker penetrate the swarm(invasion rangera t tack = 1 0, detection ranger=5)

入侵者飞行固定时间步长后认定为入侵失败，随机做出穿透集群的撤退行为，处于相应区域的个体迅速做出响应，持续了一段时间的新队形再次被局部冲散，入侵者撤出群体后，集群内再次逐渐形成新的集群。群体质心曲线在入侵者侵入群体过程中存在一段明显的波动，其表现是个体存在较大幅度的位置变化，在短暂的波动后，质心又回归平缓且保持稳定，系统回归稳定状态。如图5所示，在入侵至恢复时段（200~400步），相关函数值表现异常，400步长之后，系统回归稳定。

在这一过程中，当个体做出逃窜动作时，群体极化程度急剧减小，表现为个体间速度朝向的巨大差异性；而当系统恢复稳定性后，极化函数又近似回归为 1，表明系统协调一致性的恢复良好。这一点和位置关系展示的结果是一致的，这也说明了这一函数能够在一定程度上反应集群内部个体之间的差异大小。

最后，本文探究当入侵者侵入后原方向撤出时系统在避障之后的队形恢复情况。为了增强对比效果，设置本次入侵者所引起的预警范围rattack=5，为上组实验的一半；同时，将个体的探测范围提高一倍，r=10。在此参数组合下的群体避障效果如图6所示。

图6 入侵者撤出集群行为示意图及相关指标（入侵者预警范围 ra t tack = 5 ，个体的探测范围r=10）Fig.6 Illustration of swarm behavior and related metrices when the attacker escape from the swarm(invasion rangera t tack = 5 , detection ranger=10)

实验结果呈现出群体无论是在入侵者侵入队形后还是完全撤出队形前，集群系统都能保持很好的聚集性，甚至出现个体将入侵者包围的情况。当个体探测能力增强时，意味着个体可以更好地通过调节自身来增强系统的一致性，也可以说是系统的协调性增强。这一现象可以参考图6的速度偏差相关度函数，其震荡表明了系统不断通过个体自适应调整而调整，从而使群体呈现出能够对抗来自入侵者干扰、系统固有噪声项干扰所带来的不稳定性和混乱。

同时，群体极化函数也能反映出系统的自适应调节过程。在入侵者入侵时对极化函数造成剧烈冲击之后，极化函数一直可以维持在中等较高水平，这主要是群体个体通过不断调整速度朝向，最终趋于稳定，也意味着系统最终获得稳定。

由此可见，集群系统能够依靠自组织模型顺利躲避攻击，并且基本恢复稳定的队形集群。同时，系统中个体的感知能力增强，群体则表现出更强的稳定性，对突如其来的威胁表现出可靠的反应能力。

5 结束语

本文沿袭智能集群领域的仿生学思路，通过引入基于单体的视觉投影模型，实现了群体的自组织集群控制。通过设置不同的参数，实现了不同类型的集群行为，且得出有效结论：当噪声项wn过高时，会造成集群队形的混乱，使群体失去一致性和协调性；列队项wa具有矫正的作用，在wa较高的情况下，群体的一致性更强，单体速度朝向更加一致，队形更加整齐；wp为视觉膜投影产生特征方向的权重，局部范围内影响个体的运动决策。此外，通过设计对群体具有威胁性的入侵者行为，侵入群体内表现出很好的避障效果，群体通过设计合适的通信能力以及合适的预警范围，可以实现入侵者入侵过后群体较好程度的恢复。