基于多智能体强化学习的无人机集群对抗方法研究

杨书恒，张 栋，任 智，唐 硕

（1.西北工业大学航天学院，西安 710072；2.西北工业大学空天飞行器设计陕西省重点实验室，西安 710072）

1 引 言

近年来，随着无人机技术和人工智能算法的不断发展，实现未来空战的关键途径是空战过程智能化[1]。无人机集群作战是未来的主要作战样式，拥有更强大的动态适应性[2]，其对抗系统存在规模庞大、任务复杂、决策空间大、随机性高、状态不确定等难题。Chin和Bechtel[3-4]提出了一种基于专家系统的集群协同决策方法，通过模糊逻辑和专家知识库来帮助飞行员做出更好的机动决策。人工蜂群法[5]、萤火虫法[6]、粒子群法[7]等群体智能的方法也被广泛应用于此类问题。冉惟之[8]设计了基于群体智能的无人机协同控制算法，通过无人机集群信息素和任务分配、路径规划等的设计，实现了基于人工蜂群信息素的无人机集群协同方法。在此背景下，无人机集群逐渐成为无人机执行任务的有效方式，集群作战成为未来的发展趋势。

随着集群技术的发展，集群对抗的策略与方法逐渐成为研究的热点和关键。集群演化的规则是集群智能形成的关键。随着人工智能技术和深度强化学习技术的不断发展、突破[9]，强化学习技术被广泛应用于智能体对抗领域。强化学习主要通过奖励函数的学习来优化自身策略，被视为高级人工智能得以实现的最有潜力的方法[10]。利用深度学习与强化学习方法的结合，强化学习可通过不断迭代训练使累计奖励最大化来获得智能化策略，而深度学习可通过深层神经网络表征复杂空间的非线性和泛化性[11]。智能体能够在不同的环境下自主进行迭代优化，产生最优的集群协同策略，适用于解决规模愈加庞大、决策愈加复杂的空战问题，是解决集群对抗博弈问题的有效途径。文献[12-14]利用专家知识和神经网络相结合对神经网络进行训练，对基于专家知识的方法进行拓展，实现了稳定性强、适应动态环境的无人机集群协同决策控制方法。

现有的强化学习算法设计的动作空间和状态空间较为庞大，对计算机算力提出了相当高的要求，算力限制导致算法难以应用于无人机集群对抗环境。且其通常忽略了其他智能体的动态性，动态适应性差、不易收敛。为更好地完成集群协同控制，本文围绕以上问题展开研究，利用中心化训练、去中心化执行的方法把DDPG算法扩充为MADDPG算法，解决了多智能体博弈问题。目前，MADDPG算法已经得到大量应用，但其收敛性等仍存在不合理性，算法难以在复杂环境中得到良好应用。对于强化学习问题，动作空间、状态观测空间以及奖励空间的设计能够在极大程度上影响算法对于不同问题的收敛性，同时也对最终的训练效果起到决定性的作用。因此，本文对MADDPG算法所采用的动作空间、状态观测空间以及奖励空间进行设计，引入了更多的及时奖励以引导无人机集群涌现出更优的智能化策略，实现了算法在无人机集群对抗下的应用。最终，利用MaCA环境实现对抗仿真，验证了算法的优越性、泛化性和可实行性，具有一定的现实意义。

2 无人机集群对抗场景与模型

2.1 对抗场景设计

MaCA（Multi-agent Combat Arena）环境是中国电子科技集团公司认知与智能技术重点实验室于2019年1月推出的多智能体对抗算法研究、训练、测试和评估的环境。环境为研究利用人工智能方法解决大规模多智能体分布式对抗问题提供了很好的支撑。环境支持使用 Python 语言进行算法实现，并可调用 Tensorflow、Pytorch 等常用深度学习框架。因此本文利用其设计算法和对抗策略。

本文以MaCA环境为基础，创建了网格化的作战空域。利用环境预设的探测无人机单元和攻击无人机单元及其特性，引入红、蓝两方无人机并设定各自的性能参数与对抗策略，设计了同构智能体对抗场景和异构智能体对抗场景。

同构智能体对抗场景指对抗场景中的红、蓝两方各拥有性能、参数、类型均相同的10个攻击无人机单元，攻击无人机具备侦查、搜索、探测、干扰和攻击等功能。而异构智能体对抗场景指对抗场景中的红、蓝两方各拥有性能、参数、类型截然不同的12个攻击无人机和探测无人机，探测无人机具备侦查、搜索、探测等功能，攻击无人机功能与同构智能体对抗场景中相同。场景中的探测无人机可以模拟多频点切换下两个不同波段雷达的探测行为。场景中的攻击无人机可以模拟多频点切换下X波段雷达的指向性探测行为，以及模拟 3个不同波段雷达的指向性电子干扰行为。具体的雷达波段信息以及同构、异构对抗场景下的无人机属性均参考环境说明文档。

MaCA环境支持研究者设计的红、蓝两方多智能体算法在设定的集群对抗场景中进行博弈对抗，环境中预置了简单的基于规则实现的对抗策略。同样地，集群对抗场景也能够利用多智能体强化学习算法等方法训练后得到的参数模型，MaCA环境与算法模型和对抗场景的交互关系如图1所示。

图1 MaCA环境与对抗交互关系示意图Fig.1 Schematic diagram of the interaction between MaCA environment and confrontation

2.2 对抗模型构建

2.2.1 无人机动作行为模型

三维空间中无人机的运动过程较为复杂，其状态信息包括位置信息和速度矢量，而本文研究重点在于多智能体强化学习算法的设计，因此将其简化为二维平面问题。同时，尽可能地简化了现实空战环境中对无人机的真实约束作用，使得探测无人机仅通过全向航向角以及雷达开关和频点数对动作行为模型进行描述，攻击无人机仅通过全向航向角、雷达开关和频点数、干扰设备的开关机和频点数以及是否对目标敌机发射何种导弹4个方面对动作行为模型进行描述。因此，探测和攻击无人机单元的动作行为空间分别被简化为二维数组，数组的每一行代表了每一个无人机单元的动作值。以环境中2个探测无人机单元，10个攻击无人机单元的作战规模为例，其动作行为预设模型数组的具体内容如表1、2所示。

表1 探测无人机动作行为预设模型Table 1 Detecting UAV action behavior model

表2 攻击无人机动作行为预设模型Table 2 Attack UAV action behavior model

本文将该动作行为模型应用于基于 DQN算法的策略和基于MADDPG算法的策略中。

DQN算法仅能够处理离散、低维的动作空间，因此算法将动作空间分割为16份，每一份对应22.5°的航向角，算法仅输出[0,16]的离散数据，在训练过程中乘以每一份对应的22.5°航向角，将其映射到无人机的二维平面运动模型中。

MADDPG算法能够处理连续的动作空间，对于许多 DQN算法无法解决的问题具有良好的性能。因此，MADDPG算法采用 sigmoid激励函数作为最后一层神经网络的激励函数，以此实现[0,1]范围内的连续输出。在训练时，算法再利用先前的连续输出乘以动作空间范围，即乘以359。将[0,1]范围内的连续输出映射到无人机的二维平面运动模型中，实现了对连续动作空间的处理。

2.2.2 状态观测模型

除动作行为模型外，为实现多智能体强化学习算法对无人机集群的训练还需要建立对应的状态观测模型，多智能体强化学习算法将利用所获取的状态观测值对动作行为的选择策略进行更新，从而达到无人机集群智能化决策的目的。本文基于MaCA环境的环境底层原始观测数据对状态观测模型进行设计以使得其能够适用于多智能体强化学习算法，创建了无人机数据状态、位置状态两类状态观测模型，实现对无人机集群的训练。

探测和攻击无人机数据状态模型是二维数组，分别包括了无人机的航向角信息，航向角、远程、中程导弹剩余量信息，以此返回数据状态观测值。

探测和攻击无人机位置状态模型是四维数组，其形状为N×X×Y× 3 ，其中

式中，Xbattlefield、Ybattlefield是表示对抗场景大小的横纵坐标值，ratio是图像信息的运算比例，用于缩减运算值为适应算法的大小。

四维数组的具体内容包括探测或攻击无人机单元的数量、所有敌方目标可能出现的位置、探测敌方目标无人机的 ID编号、探测敌方目标无人机的类型（1为探测无人机，2为攻击无人机）以及友方无人机位置。敌方目标可能出现的位置和友方无人机的位置均以将对抗场景网格化的方式为其赋值，设计了统一的函数对其所在场景位置周围3×3的矩形范围内赋值，实现了获取位置等信息的目的。因此，该四维数组能有效表示探测和攻击无人机的位置状态模型，其形象化释义如图2所示。

图2 位置状态模型四维数组示意图Fig.2 Schematic diagram of four-dimensional array of position state model

2.2.3 奖励规则模型

通常，多智能体强化学习算法存在稀疏奖励问题[15]（Sparse Reward Problem），奖励信息的缺乏将导致收敛缓慢甚至无法收敛到最优策略。本文利用MaCA环境中的函数获取红、蓝两方无人机单位的单步奖励值，规定多智能体强化学习算法每经过一定步长的行动后获取一次奖励值，每局对战结束后获取一次输赢奖励值，以此消除仅依赖于对抗是否胜利的奖励规则，减小稀疏奖励问题对多智能体强化学习算法的影响。探测和攻击无人机的奖励值均为(N)的NumPy数组，每一个元素代表每一个单元的动作行为奖励值。具体奖励规则定义以及奖励值设置如表3所示。

表3 集群行为奖励规则数据列表Table 3 Swarm behavior reward rule data list

MaCA环境中默认导弹具有飞行延迟且考虑导弹的命中概率，使训练结果更具泛化性和适用性。每一轮集群对抗结束后都将进行本轮的胜负判定，每轮对战结束时，环境会利用接口向算法返回对应全局状态的奖励值。算法利用此全局状态的奖励值作为对战结束后获取的输赢奖励值，其总共分为完胜、完败、胜利、失败、平局5种结局，判定规则如下。

敌方无人机被完全摧毁时记该局对战己方无人机完胜。反之，则完败。若达到最大仿真步数，则无人机剩余多的一方记为胜利。如果红、蓝两方无人机导弹均无余量，此基础上，无人机剩余数量多的一方记为胜利。反之，则失败。

若达到最大仿真步数且两方无人机剩余数量相等时记为平局。如果红、蓝两方无人机均被摧毁，红、蓝方导弹均无余量且两方无人机剩余数量相等时记为平局。

针对以上5种不同的结局，环境将根据奖励规则数据列表返回不同的奖励值，以实现对无人机集群行为的引导。

3 对抗策略设计与实现

无人机集群对抗策略可以在基于规则的基础上建立，也可以在智能算法的基础上建立。除基于规则的方法外，对抗策略在算法对无人机的训练过程中形成，从而引导无人机涌现智能化行为，本文利用DQN算法以及设计的MADDPG算法实现了不同的对抗策略。后文将“基于 DQN算法的集群对抗策略”和“基于MADDPG算法的集群对抗策略”分别简称为“DQN策略”和“MADDPG策略”。

3.1 基于DQN算法的策略

DeepMind团队[16]基于 Q-Learning算法提出了DQN（Deep Q Network）算法，对Atari游戏中的智能体进行训练并获得了很高的分数。DQN算法在Q-Learning的基础上，使用深层神经网络表示值函数，做出了许多改进。算法对数据进行预处理，使其能够判断任务的动态性；采用ε-greedy策略对更多的状态进行探索，且随着训练次数的增加，ε将不断地衰减，实现了策略从探索为主到利用为主的转变；实现了价值模型结构的转变；利用随机初始值增强了算法的探索能力；控制帧数，以模拟人类玩家的操作；创新性地引入了样本回放缓冲区（Replay Buffer）和目标网络（Target Network），提升了算法性能。

前述算法利用的价值模型均为到R的映射，其在求解值函数时需要进行次计算，效率较低。DQN算法将模型转变为S→的形式，输出变为长度为A的向量，其中的每一个值表示对应行动的价值估计，仅需进行一次计算。Replay Buffer对交互的样本信息进行了存储，其使用包含存储样本和采集样本的过程，存储样本时若 Replay Buffer已存满则覆盖最早存储的样本，保证了其内部样本的实时性，采集样本时则从缓存中均匀且随机地采集样本进行训练。均匀采样使得每次训练采用的样本都来自多个不同的交互序列，有效提高了训练效果的稳定性和样本的利用率。

算法中引入了两个结构完全一致的模型并称之为 Target Network，原先的模型为 Behavior Network。在训练开始时，两个模型采用相同的训练参数；训练中Behavior Network与环境进行交互并得到交互的样本；学习过程中Target Network计算得出由Q-Learning算法得到的目标价值，而后用该目标价值与Behavior Network的价值估计值比较得出目标值并对Behavior Network进行更新；每完成一定轮次的迭代，将Behavior Network的网络参数赋给 Target Network，算法遵循此步骤不断迭代学习并更新策略。计算目标价值的Target Network参数将在一定的迭代轮次中被固定，能够减轻模型的波动性和不稳定性，DQN算法主要流程如图3所示。

图3 DQN算法主要流程示意图Fig.3 Schematic diagram of the main flow of the DQN algorithm

本文将 DQN算法应用于无人机集群对抗场景，以无人机集群数据状态和位置状态的观测信息作为输入，DQN算法主要参数取值为：

学习率（Learning Rate）=0.01，奖励衰减率（Reward Decay）=0.9，ε-greedy=0.9，目标网络替换步长（Replace Target Iteration）=100，记忆池大小（Memory Size）=500，训练样本个数（Batch Size）=32。其中，目标网络替换步长还作为训练参数存储步长的判断条件出现，每训练一定次数存储一次训练得到的参数模型，以便实现MaCA环境最终集群对抗仿真时进行调用。

DQN算法中的 Target Network和 Behavior Network采用卷积神经网络进行建立，其形式如表4所示。

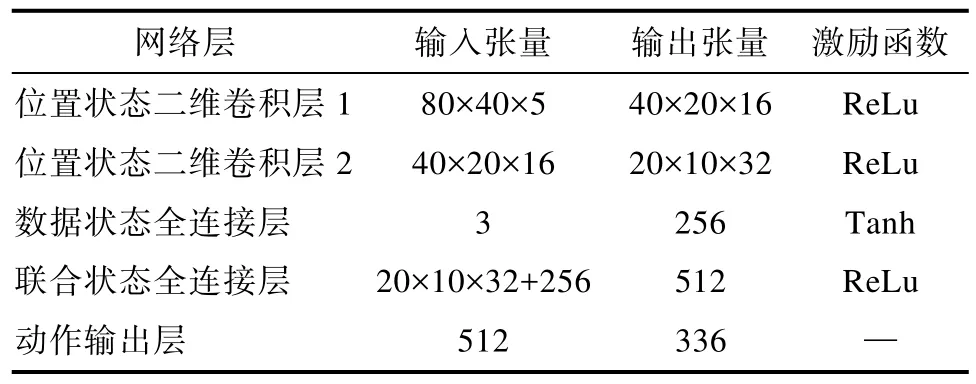
表4 DQN算法中网络结构Table 4 Network structure in DQN algorithm

在训练过程中，己方无人机易集中于地图边缘或角落，从而达到局部收敛而没有产生无人机集群对抗所需要的对抗效果，如图4(c)所示。因此，在原有奖励规则的基础上，引入了地图边缘限制，通过设置较大惩罚值的方法引导无人机避开地图边缘和角落。

引入惩罚值训练一段时间后涌现到达地图边缘后返航行为，如图4(d)所示。

在 DQN策略中，所有无人机均采用同一个神经网络进行训练，在每一个循环开始时向网络输入个体无人机不同的局部观测值，从而得到对应的动作。而采用单个神经网络造成了无人机动作单一的结果，一旦无人机的局部观测值相同，如训练初始或未观测到敌方无人机时，其涌现出相同行为，如图4(a)、(b)所示。该现象在敌方无人机数量较少时尤为明显，己方无人机过于聚集，从而难以发现地图其他位置的敌方无人机。在DQN算法中，在经过相当次数的训练后，己方无人机才能最终学习到这一策略，将无人机集群分散开来对敌方无人机展开巡航搜索，提高攻击效能，如图4(e)所示。

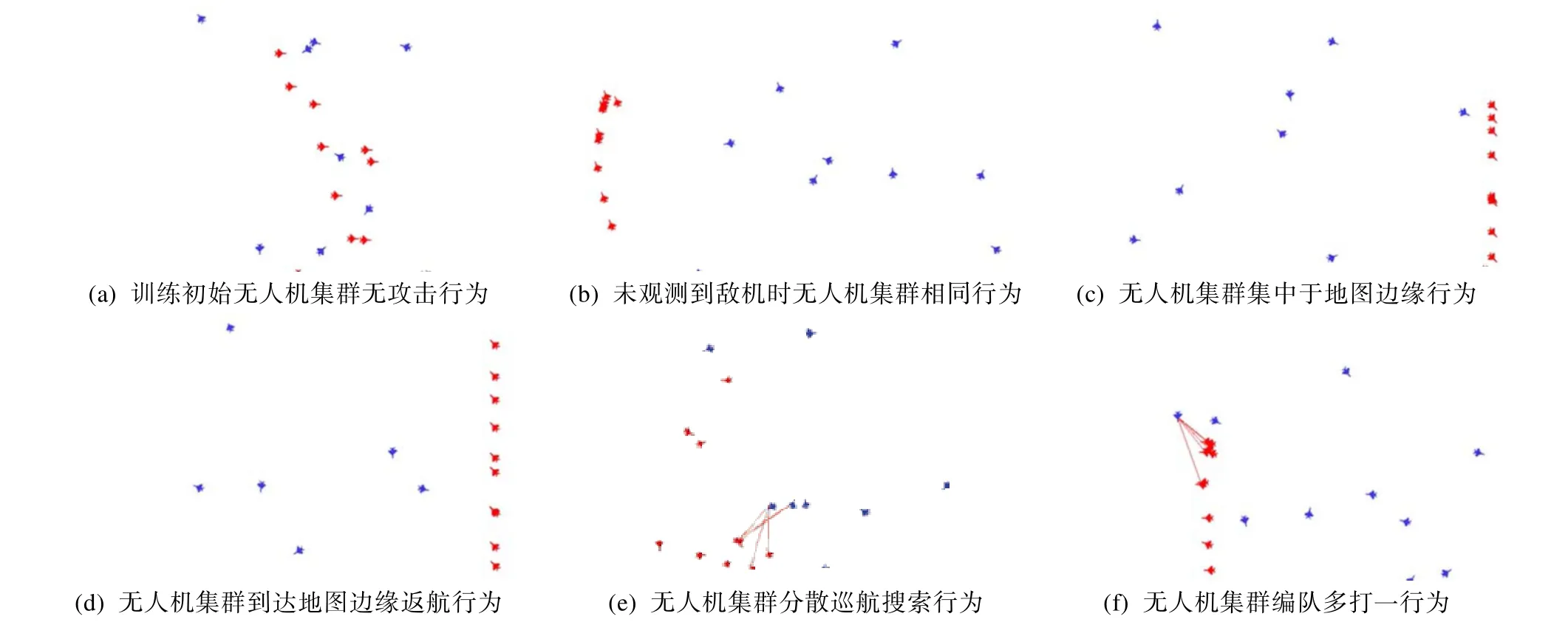
图4 DQN策略下无人机集群涌现行为示意图Fig.4 Schematic diagram of the emergence of UAV swarms under the DQN strategy

为了加快无人机学习该策略的速度，引入相对距离奖励值引导无人机对敌方无人机展开搜索。

通过以上内容，建立了本文中基于DQN算法的集群对抗策略，实现了MaCA环境对集群对抗策略的调用以及无人机集群较好的智能化行为。

3.2 基于MADDPG算法的策略

3.2.1 DDPG算法

DeepMind团队[17]将3.1节中介绍的DQN算法的创新优化方法应用到了 Deep Deterministic Policy Gradient（DDPG）算法中。DDPG算法结合了Actor-Critic算法，在两个网络中均设置了一对估计网络和现实网络，利用梯度上升寻找最大值。其中，Critic网络利用当前时刻的动作和状态对Q值进行预估，利用TD-Error计算差值；而Actor网络则输出一个能使Critic网络输出最大Q值的动作值，利用梯度上升进行更新。DDPG还采用了固定网络的方法，先将目标网络冻结，在一定次数的更新之后再将参数赋与网络。本文中利用在高斯分布中抽取随机样本的方式创造动作噪声，以增加智能体对环境的探索。

在DDPG算法中，Actor网络参数更新公式为

Critic网络参数更新公式为

此方法具有两个计算Q值的网络，Qtarget依据下一状态进行动作选择，利用 Actor网络能够切断相关性，获得良好的收敛性质，算法流程如图5所示。

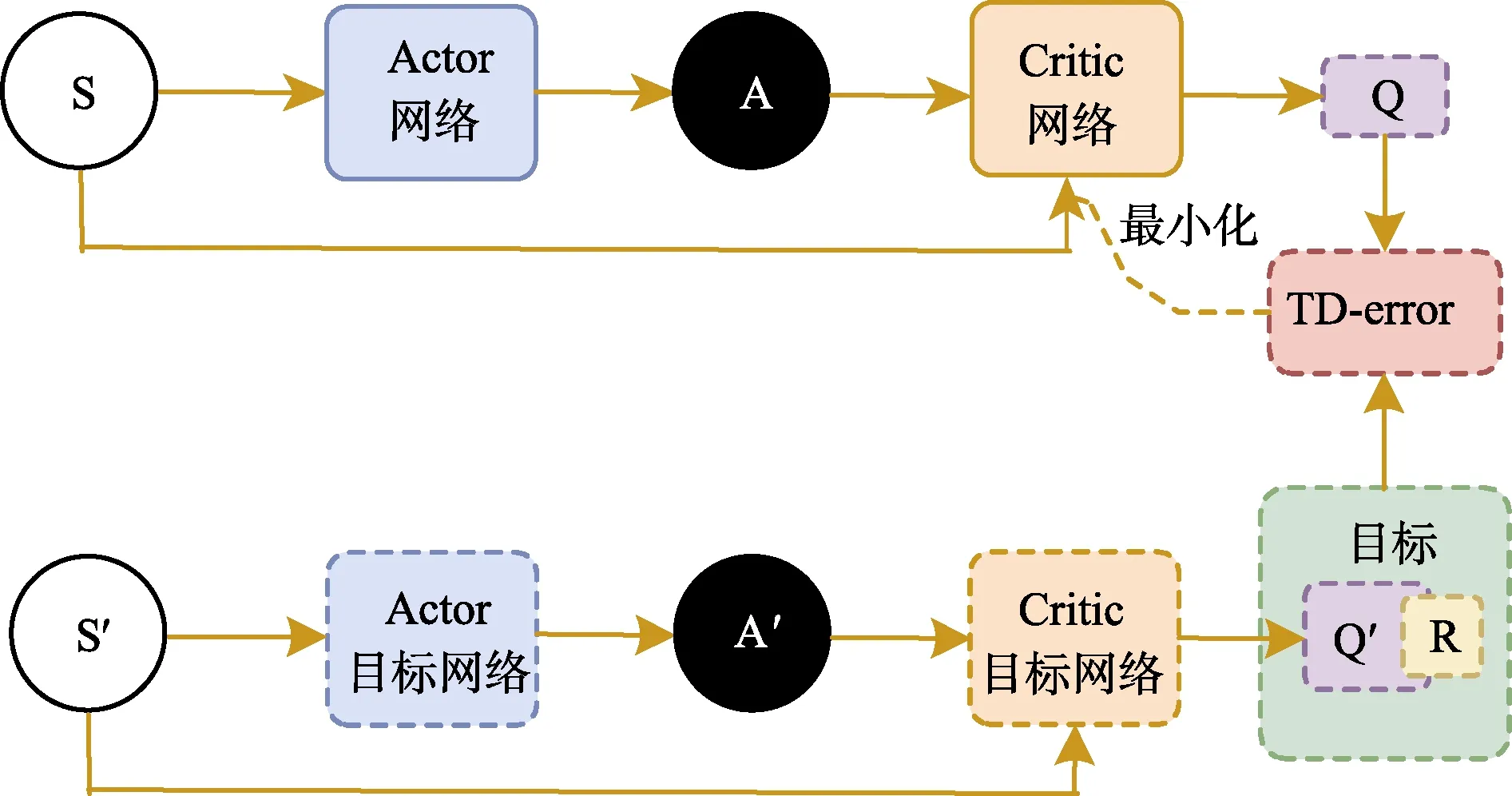
图5 DDPG算法流程示意图Fig.5 Schematic diagram of DDPG algorithm flow

3.2.2 MADDPG算法

为解决多智能体博弈等问题，传统的DQN、DDPG等强化学习算法难以获得良好的性能，其根本原因在于，多智能体博弈场景复杂、系统庞大，单个智能体的状态价值函数不仅仅依赖于自身的策略，也同时依赖于场景中其他智能体的策略。由于场景中的智能体均拥有独立的策略网络，去中心化的方式往往会引起不完全观测的问题，使得智能体智能观测到局部状态，难以选择最优策略；中心化的方式则存在执行速度缓慢的缺点，单个智能体没有决策能力，需要在通信过程中耗费大量的时间与计算。本文引入中心化训练、去中心化执行的方法，利用中央控制器收集多智能体问题中个体动作、获得的奖励值和对场景的观测来训练策略网络。训练结束后，智能体根据自身的观测和策略网络进行决策，不需要与中央控制器以及其他智能体进行通信。其算法架构如图6所示。

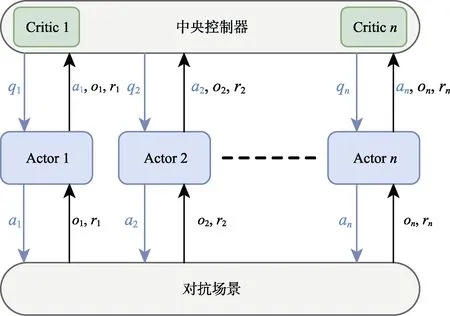
图6 MADDPG算法架构示意图Fig.6 Schematic diagram of MADDPG algorithm architecture

本文利用 5层全连接神经网络搭建 Actor网络和 Critic网络，其网络定义结构如表5、6所示。

表5 MADDPG算法中Actor网络结构Table 5 Actor network structure in MADDPG algorithm

类似DQN算法，MADDPG算法也需要引导无人机集群避开地图边缘和角落，因此引入惩罚值如式(2)。考虑到将要利用所有己方无人机的局部观测值作为输入进行集中式训练，采用第2章[L1]中的状态空间将造成状态空间过大，计算机内存占用过多无法运行的情况，因此将状态空间进行简化，简化为具有己方无人机状态信息和观测到的敌方无人机状态信息的观测值，其大小为(16,N)，将本来输入 MADDPG 算法的(5×80×40+3)×N的观测值压缩为16×N，牺牲了部分对作战地图观测的完整性，从而大大减少了状态空间的维度，提高了计算机运算速度和算法性能。其简化流程如图7所示。

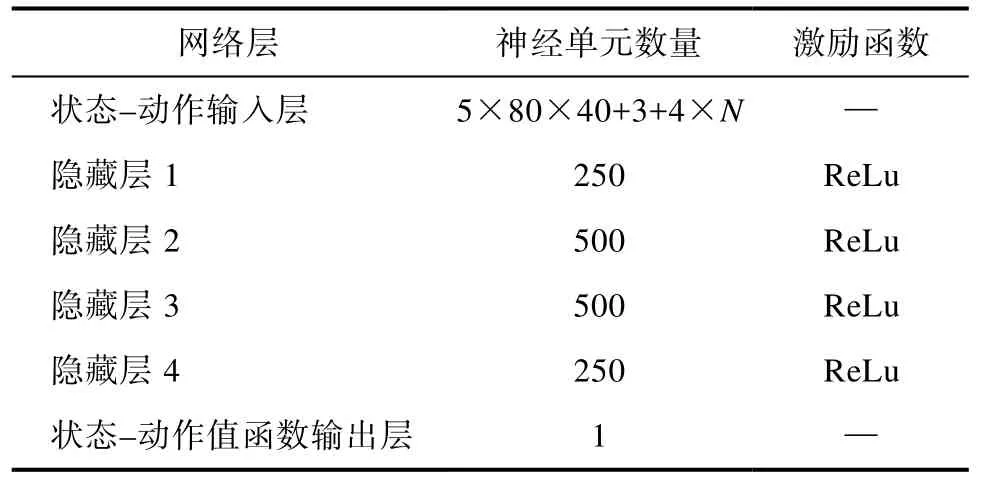
表6 MADDPG算法中Critic网络结构Table 6 Critic network structure in MADDPG algorithm

图7 MADDPG算法中状态空间简化流程示意图Fig.7 Schematic diagram of the simplified flow of state space under MADDPG strategy

简化状态空间后，针对 MADDPG算法设计的Actor状态输入层神经单元数量更改为16×N，Critic状态–动作输入层神经单元数量更改为16×N+4×N，其余层参数不变。其中相对距离dr及相对航向角qr定义如式(7)、(8)所示。

式中，xo、yo、qo表示己方无人机的位置及航向角，xt、ty、qt表示敌方无人机的位置及航向角。相对航向角几何关系如图8所示。

图8 相对航向角几何关系示意图Fig.8 Schematic diagram of the geometric relationship of the relative heading angle

在训练过程中发现对动作空间施加的高斯随机误差仍然不能带来很好的探索效果，因此在MADDPG算法中引入ε-greedy方法进行训练，增强算法训练过程中的探索能力和算法性能。

由于 Replay Buffer中的数据量级相差过大，MADDPG出现梯度消失的现象，涌现始终选择激励函数边界值的行为。因此，将状态值、动作值、奖励值全部归一化至[0,1]的范围内，从而实现 MADDPG的学习。归一化具体方式为：编号信息/10，无人机位置x、y信息/1000，航向角信息/360，导弹剩余量信息/10，及时奖励值/100。

DQN算法采用的单个神经网络涌现出难以发现地图其他位置敌方无人机的行为，而基于MADDPG算法的对抗策略采用了不同神经网络进行构建。每一个无人机均拥有一个独立的神经网络和Actor-Critic结构，仅Replay Buffer采用同一个。涌现出了较好的无人机动作。不再产生相同的动作引起的聚集现象，实现快速搜索无人机的效果。

本文将训练过程分为探索策略学习阶段、攻击策略学习阶段以及追击策略学习阶段。在训练过程中发现，无人机难以涌现最终的追击行为，因此在原有的奖励规则基础上引入更多的及时奖励，以引导无人机涌现更好的智能化行为，奖励值更改为

通过以上内容，建立了本文中基于 MADDPG算法的集群对抗策略，实现了MaCA环境对集群对抗策略的调用以及优于DQN算法的智能化行为。

4 仿真结果及分析

为简化仿真内容，体现仿真效果，本文采用同构对抗场景并将对抗场景地图大小修正为800×400，以匹配真实空战场景的无人机集群模式，同时减小状态空间的大小，适应计算机算力。为缩短训练时间，在更短的训练步长中看出训练效果和趋势，将敌方基于规则的策略简化为不附带任何攻击行为的基于规则的策略，利用该策略分别与基于DQN算法的策略和基于MADDPG算法的策略进行对抗训练并获得仿真结果，以此对比DQN算法和MADDPG算法训练效果及性能，达到本文的研究目的。

本文中训练所采用的硬件配置是：Intel(R)Core(TM) i7-9750H CPU@2.60GHz 2.59 GHz处理器以及GeForce GTX 1660 Ti显卡。DQN算法采用的深度强化学习框架为 Pytorch，MADDPG算法采用的深度强化学习框架为 Tensorflow，本文在该硬件和框架下实现了算法的设计与仿真。

4.1 DQN算法

MaCA环境自身也提供了 DQN算法，本文对其进行了改进。环境提供的 DQN算法仅能实现算法的训练与学习，其收敛效果以及涌现的智能化策略不理想，难以得到良好的应用。本文对其的动作空间、状态空间以及奖励规则等做出了设计，引入了更多的及时奖励，如3.1节中的式(2)、式(3)等所示。引导DQN算法涌现了良好的智能化策略，实现了算法在无人机集群对抗下的高效应用。

训练结果如图4所示。随着训练次数的增加，无人机动作奖励值也随之变化，正奖励值的获得率不断增加，DQN算法的lost值维持在0左右，如图9所示。

图9 DQN策略奖励、lost值随训练次数变化示意图Fig.9 Schematic diagram of reward and lost value changing with training times under DQN strategy

由训练结果可知，DQN策略下无人机集群行为不断趋向收敛，涌现出了如图4(e)、4(f)所示的集群编队、多打一等智能化行为，体现了基于DQN算法的集群策略的智能性和强化学习方法的有效性。

同时，算法在大步长训练下仍未涌现良好的追击状态，且由于使用同一个神经网络进行训练，不同无人机个体之间的策略相互耦合，导致训练缓慢且涌现的智能化行为较为低效。

4.2 MADDPG算法

在简化状态空间、更改奖励值后，为提高MADDPG算法的泛化性，本文同时也利用DQN策略对MADDPG算法进行训练，对基于规则策略的训练结果进行扩充，其训练结果如图10所示。

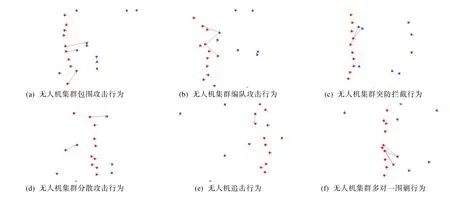
图10 MADDPG策略下无人机集群涌现行为示意图Fig.10 Schematic diagram of the emergence of UAV swarms under the MADDPG strategy

MADDPG算法是基于传统 DDPG算法的改进，其引入了中心化训练、去中心化执行的方法，实现了更高效的训练和更具智能化的策略。若采用DDPG算法进行训练，其仍能够处理连续动作空间问题，但所有的无人机均采用同一个神经网络进行构建，容易涌现单一行为。这是两种算法最主要的区别，同时也是本文所要验证的优点。DDPG算法的单一行为现象可以在DQN算法的仿真结果中得到体现，因此本文直接利用DQN算法与MADDPG算法进行横向比较来验证算法采用集中式训练、分布式执行的优越性。

随着训练的不断进行，无人机集群涌现出一系列攻击行为。

包围攻击行为：两端无人机以更接近敌方无人机的姿态进行包围攻击，如图10(a)所示。

编队攻击行为：无人机以多排无人机编队的姿态进行编队攻击，如图10(b)所示。

突防拦截行为：无人机优先对试图突防的敌方无人机进行拦截攻击，如图10(c)所示。

分散攻击行为：为实现更高的打击及探测效率，无人机集群分散开来分别对敌方无人机进行攻击，如图10(d)所示。

追击行为：随着训练步数不断增大，无人机涌现出对敌方无人机的追击行为，相比DQN策略的训练实现了更高的打击效率，如图10(e)所示。

多对一围剿行为：随着训练步数增大，无人机集群倾向于实现对敌方无人机的围剿，产生了许多多对一的攻击行为，以更高的效率实现毁伤效果，如图10(f)所示。

随着训练次数的增加，无人机动作奖励值也随之变化，正奖励值的获得率不断增加，lost值在训练过程中快速下降后基本趋于稳定，如图11所示。

图11 MADDPG策略奖励、lost值随训练次数变化示意图Fig.11 Schematic diagram of reward and lost value changing with training times under MADDPG strategy

在 3500次左右的训练中，横向比较MADDPG策略与DQN策略所涌现出的行为以及获得的奖励值等。对比图9与图11，两图均为经过3500次左右训练获得的奖励和lost值随训练次数的变化图。能够看出，两种算法中智能体随训练次数增加获取奖励值的概率均不断增大，lost值均迅速减小后并趋于稳定，其在一定程度上体现了算法的收敛性。该横向比较可以看出，MADDPG算法相比于 DQN算法涌现出了更大的优势。DQN算法在大步长的训练下仍涌现出追击行为，而MADDPG则涌现出了智能化的追击行为，在更短的训练步长中达到了更好的效果，证明了MADDPG算法采用集中式训练、分布式执行的优越性。从多策略训练与仅规则策略训练的MADDPG策略涌现的不同行为（如追击行为等）可以看出，利用不同策略进行训练的 MADDPG算法拥有更好的泛化性，在复杂、动态的战场环境中具有更优越的动态适应性，展现了本文对其泛化性的训练效果。

5 结束语

本文研究基于多智能体强化学习的无人机集群对抗方法，区别于传统的强化学习方法，将扩展的多智能体强化学习算法应用于无人机集群对抗问题中，实现了多种策略对算法的训练。利用智能体行为、奖励的可视化展示了算法的训练效果，验证了算法的有效性、适应性。多智能体对抗博弈策略在一些实际领域具有应用价值[18]，而算法的训练效率、工程实践的适用性、训练结果的泛化性等仍是应用中存在的问题，算法的创新、工程应用是未来研究关键。