基于攻击成本的信号调制分类对抗样本检测算法

宣 琦,周 涛

(浙江工业大学 网络空间安全研究院,浙江 杭州 310023)

无线电信号的调制分类技术在军民领域得到了广泛应用,例如在军事作战场景用于实时战场通信、控制导弹和引导战舰等;广播电台进行广播时用于信号的解调等。信号调制分类主要由特征提取和分类识别两个步骤组成。传统的特征提取方法包含大量数学计算和多次高阶特征提取步骤[1],实现较为复杂。此外,随着无线电通信技术快速发展,现代无线电通信环境变得十分复杂,传统的调制分类方法易受到干扰,不仅需要进行多次解调对比才能得到结果,而且准确率不高。随着计算机算力水平的不断提升,深度神经网络(Deep neural networks,DNN)被广泛应用于各种任务,例如图像分类[2-3]、语音识别[4-5]和自动驾驶[6-7]等,均取得了出色的效果。因此,越来越多的研究者尝试将深度神经网络应用到信号调制分类任务中。O’Shea等[8]率先将深度神经网络应用到了无线电信号调制分类任务中,抛弃了传统的利用特征提取器和分析似然比的方式,利用神经网络强大的学习能力捕捉信号数据的高阶特征,在公开数据集上达到了80%的平均分类准确率。Peng等[9]将原始信号数据进行映射转换成对应的星座图,并输入至卷积神经网络进行训练,在8～14 db信噪比样本分类上明显优于传统支持向量机分类器,分类精度平均提升了7.75%左右,初步探索了信号数据与图像数据的关联性。但在深度神经网络强大的背后,仍然存在不可忽视的安全性问题。Szegedy等[10]研究发现:深度神经网络易受到对抗样本的干扰,攻击者只需在原始图像上添加经过设计的扰动,就可以欺骗深度神经网络,致使其给出错误的预测结果,而这些扰动通常无法被肉眼观测。针对这个问题,研究者们提出了大量的对抗样本防御机制,防御机制主要分为传统防御和对抗样本检测两个方向。传统防御虽然可以通过对抗训练[11]、梯度掩盖[12]和防御蒸馏[13]等方式提高深度神经网络的鲁棒性来防御对抗样本,但是这些防御机制存在各种局限,例如重训练会带来昂贵的计算成本、影响原始模型的分类精度等,并且Carlini等[14]的研究发现通过对攻击参数的微调即可绕过这些防御手段。对抗样本检测则通过寻找正常样本与对抗样本之间的差异,通过阈值、预测不一致和检测网络等形式检测对抗样本,防止其误导目标模型。目前主流的对抗检测算法有基于降噪器的特征压缩[15]、MagNet[16]和自适应降噪[17];基于神经元激活状态的I-defender[18]、SafetyNet[19]和特征距离空间算法[20];基于样本在某个子空间中分布的贝叶斯不确定性估计[21]和局部内在维度度量[21]等。这些检测算法虽然都在图像分类领域取得了较好的检测效果,但是信号调制分类领域的检测算法研究还处于起步阶段,尚未形成完整的检测体系。直接迁移图像分类领域的检测算法并不能在信号这一数据类型上取得很好的检测效果,信号调制分类领域亟须一个可靠并且有效的对抗样本检测机制,保障各项分类任务的安全运行。

针对上述问题,笔者提出了一种基于攻击成本的信号调制分类对抗样本检测算法,使用攻击成本来表征样本与决策边界面的相对位置,对抗样本通常会更靠近决策边界面,因此对其进行攻击所需的成本更少。首先,使用攻击迭代次数衡量样本的攻击成本;然后,通过KNN算法(K-NearestNeighbor,K最邻近)计算待测样本与邻居样本攻击迭代次数之间的Z-Score分数区分对抗样本与正常样本;最后,对检测算法进行了实现验证,在6种主流对抗攻击算法下均能达到80%以上的检测准确率。

1 背景介绍

1.1 对抗攻击深度神经网络

根据原理,可以认为对抗攻击深度神经网络是一个需要拟合的函数f,其使用神经元从被标记的训练数据中提取特征。假设X为输入空间;Y为预测结果空间;P(X,Y)为X×Y上的数据分布,则称f:X→Y为预测函数。

对抗样本这个概念最早由Szegedy等提出,在原始输入样本x上添加精心设计的扰动,得到新的输入x′,DNN模型会给新的输入x′一个错误的预测标签,x′被称为对抗样本。x′满足f(x)≠f(x′),并且x′-x<ε,其中ε为可添加的最大扰动,ε满足ε∈R。

对抗样本虽然威胁了DNN的安全,但是其本身具有重大的研究意义,可以帮助我们更深入地了解DNN的底层原理。因此,研究者们相继提出了许多对抗攻击算法,笔者主要介绍在检测算法实现和评估中涉及的主流对抗攻击算法。

1) 快速梯度下降算法(Fast gradient sign method,FGSM)[22],是深度神经网络梯度生成对抗样本的攻击算法。其基于L∞距离计算输入样本x的每个值的梯度,寻找扰动方向,使目标模型的损失函数增加,从而改变样本的预测标签,表达式为

(1)

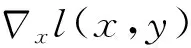
2) 基本迭代算法(Basic iterative menthod,BIM)[23],是FGSM的一种改进,也被称为迭代版的FGSM。其迭代地执行n次FGSM,并在每一次的迭代过程中裁剪结果值,保证结果维持在输入范围,表达式为

(2)

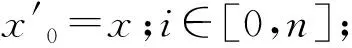
3) 投影梯度下降算法(Projected gradient descent,PGD)[24],是一种类似BIM的迭代攻击算法,为了找到模型的最大损失,其首先利用L∞随机初始化扰动,在每次迭代中将扰动投影到有效范围中,表达式为

(3)

式中Proj用于将添加扰动后的对抗样本投影至ε-L∞领域和输入的有效范围中。

4) 基于雅可比的显著图攻击(Jacobian-based saliency map attack,JSMA)[25],是一种使用雅可比显著图生成对抗样本的攻击方法。其将深度神经网络的梯度构建成显著性矩阵,对矩阵中所有值的重要性进行排序,选择显著性最大的值进行修改,增加样本被分类为目标标签t的概率,并不断重复这一过程,直到攻击成功。

5) 深度愚弄攻击(DeepFool)[26],是一种基于超平面分类的攻击方法,其在每次迭代过程中,计算样本当前位置与周围所有类别的超平面(即决策边界面)的线性距离,选择最小的距离决策边界面设计扰动,添加扰动使样本移动到该决策边界面,直至样本被分类错误。

6) 基于优化的对抗攻击(Carlini & Wagner,CW)[27],是一种基于优化的攻击算法,其将对抗样本作为一个变量,优化以下两个目标:最小化对抗样本与原始样本之间差异;最大化对抗样本错误分类的预测置信度。

1.2 对抗样本检测

给定一个DNN模型f,一个输入样本x,使用检测器D判断该输入样本x是否是对抗样本。表达式为

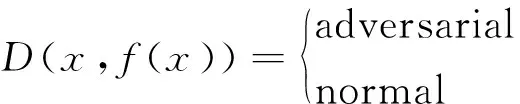
(4)

该问题的本质是如何找到一种模式或表征区分正常样本和对抗样本。考虑如下防御场景:攻击者可以访问DNN的所有信息,并且没有任何关于攻击的信息,只可以使用正常样本构建检测器。

2 理论与方法

2.1 样本分布理论

笔者提出的检测算法基于在一定扰动范围内,对抗样本会比正常样本更接近模型的决策边界面的理论,可以从神经网络训练和对抗样本生成过程这两个角度理解该理论。神经网络的训练通常要经历多次迭代,在每次迭代中训练数据首先会被分成多个批次进行训练,然后通过梯度下降等方式更新参数,这样训练得到的模型通常具有很好的泛化性。样本分布示意图如图1所示。由图1可知:在该模型所定义的子空间中,正常样本的分布会更加聚集,并且会远离决策边界面,而对抗样本虽然和正常样本属于一个类别,但其所处的位置会更加接近决策边界面。

图1 样本分布示意图Fig.1 Sample distribution diagram

此外,在生成对抗样本的过程中,所添加的扰动会受到一些条件的约束,例如最小扰动、不可观测性、目标标签攻击和攻击速度等,而这些条件往往会造成所生成的对抗样本不够“鲁棒”,处于决策边界面附近。可以利用这一特质设计表征方法区分正常样本与对抗样本,Feinman等[21]提出了核密度估计(KD)和贝叶斯不确定性估计(BU)算法;Wang等[28]设计了标签变化率算法。虽然他们的算法都在图像分类领域取得了90%以上的平均检测准确率,实验结果也证明了该理论的正确性,但直接将这些方法迁移至信号调制分类并不能取得很好的检测效果,或者是效率不高,不适用于实际应用。笔者参照Feinman等[21]的工作,在信号调制分类任务中使用深度学习基础模型(Network in network,NIN)[29]复现了KD和BU检测算法,在单指标检测下,对FGSM,BIM,PGD,JSMA,DeepFool和CW这6种攻击算法的平均检测准确率分别为60.9%和53%;结合KD和BU指标也仅达到了65.3%的平均检测准确率。标签变化率方法需要大量的突变模型参与计算,平均每个突变模型需要6 s的加载时间,按照平均80个突变模型得到检测结果的标准,每个样本需要经历480 s的检测耗时。如果提前将所有突变模型加载至内存中,需要耗费大量的内存与显存空间,对硬件设备平要求较高。

2.2 攻击成本表征

为了更加高效且准确地检测信号调制分类任务中的对抗样本,参照Zhao等[30]的方法,使用攻击成本来衡量样本到决策边界面的距离,假设正常样本因为离决策边界面更远所以具有更高的攻击成本,而对抗样本的攻击成本则偏低。因此,可以使用现有的攻击方法攻击待测样本从而判断其是否为对抗样本。使用攻击成本进行对抗样本检测,需要解决如何表征不同类型攻击的攻击成本和验证表征方式的有效性这两个问题。

1) 如何表征不同类型的攻击方法的攻击成本。攻击成本最直接的一个衡量方式是攻击的耗时,但攻击耗时受到硬件设备性能的影响,在不同设备、功率下的表现无法保持统一。因此采用攻击迭代次数的衡量方式。这种衡量方式仅适用于迭代攻击,以BIM算法为例,BIM在每次迭代过程中不断计算梯度,寻找扰动方向,添加的对抗扰动将样本推向决策边界面,在这个过程中,对抗样本由于本身靠近决策边界面,因此其所需要的攻击迭代次数相较于远离决策边界面的正常样本更少。同时,在相同设备情况下,因为计算机执行了同样大小的矩阵运算,每一次攻击迭代中的计算耗时几乎是相等的。使用JSMA,BIM-L1和BIM-L2攻击算法对600个随机选取正常样本进行攻击并记录其攻击迭代次数与攻击耗时,结果如图2所示。由图2可知:攻击耗时随迭代次数增多而上升,总体呈正相关趋势。因此攻击迭代次数可以用来衡量样本的攻击成本。

图2 样本攻击耗时与迭代次数关系图Fig.2 The relationship between the sample attack time and the number of iterations

2) 攻击迭代次数衡量样本攻击成本的有效性。在RML2016.10.a数据集[8]上使用1.2小节中提到的6种对抗攻击算法生成对抗样本以及正常样本,每种类型随机选取1 000个样本,保证样本一一对应,使用JSMA,BIM-L1和BIM-L2攻击算法对这些样本进行攻击并记录攻击迭代次数,计算所有样本攻击迭代次数之间的欧式距离,并绘制成热力图,具体情况如图3所示。图3中Normal代表正常样本。由图3可知:正常样本与对抗样本之间的平均欧式距离明显大于对抗样本互相之间的平均欧式距离。这表明正常样本与对抗样本在子空间中所处位置具有明显区分。此外,不同类型的对抗样本之间的平均欧式距离也较为接近,这表明不同攻击算法可能会生成攻击成本相近的对抗样本。因此,使用攻击迭代次数衡量样本的攻击成本具备可行性。

1—FGSM; 2—BIM-L1; 3—JSMA; 4—PGD; 5—DeepFool; 6—CW; 7—Normal。图3 攻击迭代次数平均欧式距离热力图Fig.3 Heat map of average Euclidean distance of attack iterations

2.3 检测方案

根据上述理论,笔者提出了一种基于攻击成本的信号调制分类对抗样本检测算法。该算法没有直接量化攻击迭代次数作为检测依据,而是加入最近邻算法和Z-Score(标准分),2 420个正常样本的攻击迭代次数如图4所示。其中,每类样本220个,按照类别顺序排列。通过观察正常样本的攻击迭代次数与类别关系可以发现:不同类别的正常样本攻击迭代次数之间也会有较大差异,如果单纯使用量化的攻击次数作为检测依据会使某些类别的样本误判率偏高。加入最近邻算法和Z-Score是为了最大程度地利用样本与其周围的邻居信息作为不同类别样本检测的参考依据。该方法的核心思想是通过寻找待测样本x在训练集中的k个最近邻样本,计算待测样本攻击迭代次数与最近邻居样本攻击迭代次数的Z-Score实现样本区分。

图4 攻击迭代次数与样本类别关系图Fig.4 Relationship between attack iteration times and sample category

Z-Score在统计学中常用来刻画目标值偏离均值的程度,即偏离均值多少个标准差。在该检测任务中表达式为

(5)

式中:i为待测样本的攻击迭代次数;μ为待测样本的最近邻样本的攻击迭代次数的均值;σ为最近邻样本的攻击迭代次数的标准差。对抗样本需要的攻击成本少,对应的攻击迭代次数通常会小于均值,因此对抗样本的Z-Score会低于正常样本。

此外,为了保证查询待测样本x的最近邻样本时的效率,使用了K维树(K-dimensional tree,KD-Tree)的数据结构,其是一种对K维空间中的实例点进行存储以便对其进行快速检索的树形数据结构,可以将查询的平均时间复杂度降低至O(logn)。检测算法的具体流程如图5所示。

图5 基于攻击成本的信号调制分类对抗样本检测框架Fig.5 Signal modulation classification adversarial sample detection algorithm framework based on attack cost

具体流程为

1) 使用训练集中的正常样本构建用于最近邻查询的KD-Tree数据结构,KD-Tree的所有节点存储了样本的索引值。

2) 对训练集的正常样本进行攻击并记录攻击迭代次数,以样本的索引值作为key,攻击迭代次数作为value,将所有数据存储为哈希表结构。

3) 首先输入待测样本对其进行攻击并记录攻击迭代次数；然后在KD-Tree中查询待测样本的k个最近邻居样本,获取其索引值。

4) 根据索引值在哈希表中查询最近邻样本的攻击迭代次数。

5) 计算待测样本与最近邻样本攻击迭代次数之间的Z-Score分数。

6) 比较所得Z-Score分数与阈值的大小,若大于阈值则判断为正常样本；若小于阈值,则判断为对抗样本。

以上步骤为使用一种迭代攻击算法进行对抗样本检测的情况,也可以结合多种迭代攻击算法进检测,采用投票机制决定最终检测结果,实现更加全面的对抗样本检测。

3 实验与分析

3.1 实验环境配置

评估检测算法有效性的具体软硬件配置如表1所示。CPU使用Intel(R) Xeon(R) E5-2650,GPU使用专业深度学习显卡Tesla V100-PCIE-16 GB。软件层面操作系统使用Ubuntu 16.04.6,深度学习模型及检测算法实现框架为TensorFlow-GPU 1.14。

表1 实验环境配置

在实验数据集方面,选择了信号调制分类领域的公开数据集RML2016.10a,该数据集使用GNU Radio合成IQ信号样本。总共为11个类别,代表样本的调制类型,其中数字调制包括64QAM,QPSK,8PSK,16QAM,BPSK,BFSK,CPFSK和PAM4,模拟调制包括WB-FM,AM-SSB和AM-DSB。该数据集共包含220 000个调制信号样本,每类信号信噪比范围为-20～18 db,每个信号样本大小为1 282,分别对应I和Q两个通道,训练集与测试集比例为4∶1。

信号调制分类模型使用了Lin等[29]在2014年提出的NIN模型,其网络结构如图6所示。NIN不仅抛弃了传统的线性卷积结构,使用多层感知器代替,大大增加了网络的非线性表达能力，而且还加入了全局均值池化层代替全连接层。使用NIN模型在RML2016.10a数据集的测试集中达到了87.5%的分类准确率。

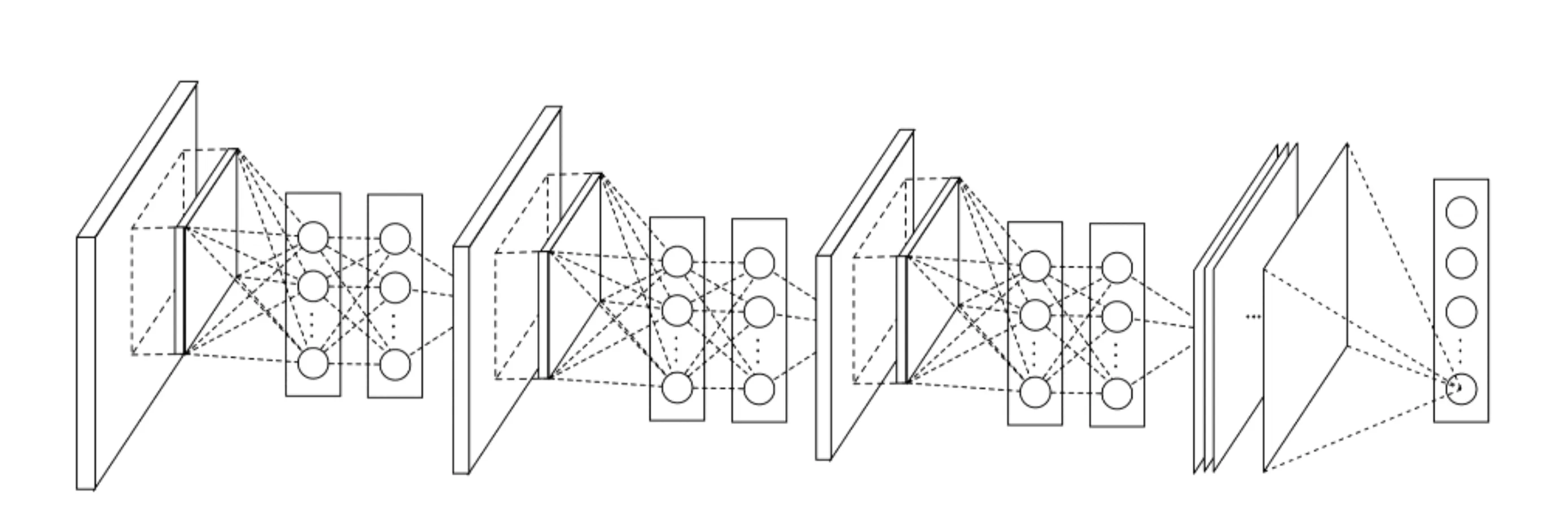
图6 NIN网络结构[29]Fig.6 NIN network structure

3.2 实验设置

为了验证检测算法对正常样本和对抗样本的区分度,以及检测算法对不同类型对抗样本的检测效果,使用1.1中提到的6种白盒对抗攻击算法,对测试集样本进行攻击,只保留攻击成功的样本,其中BIM攻击算法使用了L1和L2两组距离实现,将这7类对抗样本分别与原始测试集样本组合成一个二分类测试集,每类有2 200个测试样本,原始测试集正常样本的标签为0,所有的对抗样本标签为1。在比较了JSMA,BIM-L1,BIM-L2,PGD,DeepFool和CW这6种迭代攻击算法后最终选择了JSMA,BIM-L1,BIM-L2这3种攻击算法衡量样本的攻击迭代次数。其中PGD和DeepFool攻击算法的攻击迭代次数普遍较少,大部分样本都可以在10次迭代以内就攻击成功,区分度不够明显;CW攻击算法由于是基于优化的攻击,因此它的迭代次数呈现一种随机性状态,波动较大,没有明显的趋势,并且速度较慢,不适合快速检测任务。而JSMA,BIM-L1,BIM-L2这3种攻击算法,攻击迭代次数在数量与区分度之间都符合的检测要求,并且攻击速度较快,适合快速检测任务。

3.3 评估指标

使用了4种评估指标用于评价检测算法的检测效果,分别为检测准确率、精确率、召回率和F1-Score。对抗样本为二分类问题的正类,正常样本为负类,预测结果可分为正样本被预测为正类的数量TP、负样本预测为正类的数量FP、正样本预测为负类的数量FN和负样本预测为负类的数量TN这4种情况。这4种评估指标的计算式分别为

1) 准确率(Acc):

(6)

2) 精确率(Precision):

(7)

3) 召回率(Recall):

(8)

4) 对精确率和召回率的加权平均(F1-Score):

(9)

3.4 实验结果与分析

使用JSMA,BIM-L1和BIM-L2这3种攻击算法进行信号调制分类对抗样本检测的实验结果分别如表2～4所示。检测结果表明:检测算法在7类对抗样本下均有较好的检测效果,平均检测准确率分别达到了81.78%,88.33%和88.95%,并且对所有类的对抗样本检测表现较为稳定,没有出现对某一类样本检测效果很差或者无效的极端场景,泛化能力较强。另外,检测算法在保持较高水平的F1-Score情况下,对部分对抗样本的检测召回率达到了1,表明检测算法具有较为强大的对抗样本区分能力。

表2 JSMA攻击成本检测结果

表3 BIM-L1攻击成本检测结果

表4 BIM-L2攻击成本检测结果

为了更加直观地了解在笔者检测算法的机制下正常样本与对抗样本之间的差异,将所有测试集样本以Z-Score分数作为特征绘制了箱形图,具体如图7所示。箱形图提供了中位数、均值和上下分位点的信息,可以提供有关数据位置和分散情况等关键信息。由图7可知:正常样本的主体分布明显大于对抗样本的主体部分,正常样本普遍分布在0附近,而对抗样本普遍分布在0以下。在图7(a)中使用JSMA进行检测,对抗样本分布的上边缘较超过了正常样本分布的中位数位置,而在图7(b,c)中使用BIM-L1和BIM-L2进行检测,对抗样本的上边缘位置也明显低于正常样本下四分位置,这也与笔者实验结果相符合,相较于JSMA,BIM-L1和BIM-L2具有更好的检测效果。但无论是哪种攻击方法用于检测,正常样本下边缘位置仍与对抗样本有交集部分,关于这种现象,笔者认为这些样本在该模型的子空间中本身就处于靠近决策边界面的位置,与模型本身分类精度有关,可以将其理解为异常样本,虽然这些样本会被误判,但是它们的数量很少,不会影响检测算法的整体效果。

1—Normal; 2—FGSM; 3—BIM-L1; 4—BIM-L2; 5—PGD; 6—DeepFool; 7—CW。图7 攻击本检测箱形图Fig.7 Attack cost detection box plot

4 结 论

针对基于深度神经网络的无线电信号调制分类任务面临的安全性问题,提出了一种基于攻击成本的信号调制分类对抗样本检测算法。相较于正常样本,对抗样本更靠近模型的决策边界面,因此拥有更少的攻击成本。该方法利用攻击迭代次数衡量样本的攻击成本,通过寻找待测样本x在训练集中的k个最近邻样本,计算待测样本攻击迭代次数与最近邻居样本攻击迭代次数的Z-Score(标准分)实现检测。使用6种主流白盒攻击算法生成用于评估的对抗样本,使用JSMA,BIM-L1,BIM-L2这3种攻击算法衡量样本的攻击成本,分别取得了81.78%,88.33%和88.95%的平均检测准确率,表明该算法具有稳定且优越的检测效果。下一步的研究将针对正常样本中可能会出现的异常样本进行优化研究,使检测算法具备更加全面的检测能力。