铝尾矿泥浆中微米级细颗粒自然沉降规律研究
2022-11-29孙刚臣张喜伟
邓 旭, 孙刚臣, 张喜伟
1. 桂林理工大学 土木与建筑工程学院, 广西 桂林 541004; 2. 广西建筑新能源与节能重点实验室, 广西 桂林 541004
1 研究背景
中国是一个矿产资源大国, 铝土资源的储量位居世界第4, 随着中国氧化铝工业的高速发展, 氧化铝产量逐年增高, 而氧化铝生产时需要用到大量的水来冲洗原矿, 洗矿后的废水经过沉降, 形成的高含水量泥浆称之为矿泥, 据统计, 每生产1 t 氧化铝需要排出矿泥1~2.5 t[1]。 仅2015 年中国的矿泥排放量就超过8 000 万t[2], 截至2016 年, 中国矿泥累计存量超过3.5 亿t[3], 如此大量的尾矿堆积, 不仅浪费了大量的土地资源, 还给自然环境与人类造成大量污染及巨大危害。
尾矿泥在工业生产中的回收方式主要为露天堆存使其自由沉降, 使矿泥颗粒自由迁移后脱水回收, 在自由沉降中, 颗粒主要受到颗粒自身的重力、 介质浮力和颗粒粒径组成的影响[4]。 根据广西冶金研究所《那豆矿区堆积铝土矿洗矿工业试验报告》 提供的矿泥粒度组成分析: “矿泥很细, 尤以粘、 胶粒含量高,其中小于75 μm 的细微颗粒平均质量占比超过90%,按照土工试验规程中的土的分类方法, 其属于高液限粉土。” 梁越等[5]认为在反滤试验中基料颗粒粒径越小, 试验过程中水力梯度从颗粒起动临界水力梯度值到整体破坏水力梯度值的变化量更小, 整体破坏发生得越突然; 反之粒径越大, 颗粒起动水力梯度至整体破坏水力梯度的变化量更大, 整体破坏所需时间越长。
梁越等[5]研究发现均匀土基料级配相同情况下,颗粒临界水力梯度与破坏水力梯度与滤层颗粒粒径呈线性关系。 减小滤层颗粒粒径一定程度上可以提高基料颗粒起动临界水力梯度, 但减少达到一定值后继续减小滤层颗粒粒径临界水力梯度反而减小。 滤层颗粒级配与基料颗粒级配之间存在最佳级配。 使滤层反滤效果达到最大, 基料不均匀系数Cu=d60/d10 较小时, 基料颗粒越均匀, 颗粒级配越单一, 颗粒反而越不容易起动。 当颗粒不均匀系数达到1.86 以后, 基料颗粒起动临界水力梯度随不均匀系数增大基本保持不变。 肖芳玲、 张爱军指出, 易流失土颗粒主要是小颗粒, 皆小于被保护土中值粒径d50[6]。 张升等[7]在研究砂—粉土混合料在列车荷载作用下细颗粒迁移机制时发现, 细颗粒迁移现象试样浅层区较为显著, 且颗粒粒径越细, 迁移量总体越明显。 随着时间的推移, 细颗粒迁移促使试样轴向颗粒级配的差异性逐渐增强, 试样轴向水力性质的改变进一步加剧孔隙水和细颗粒发生迁移。 陈轮[8]和颜永国等[9]认为, 在应力条件和土颗粒属性条件一定的情况下, 滤层表面土颗粒拱结构的形成受颗粒级配的影响。 而土拱结构或团聚体的形成也会反作用于土颗粒的迁移过程。Chang[10]指出, 细粒含量多、 级配差、 粘聚力小、内部不稳定的土, 在相同情况下更容易迁移。
由上可知, 国内外对矿泥浆悬浮颗粒的迁移已经进行了一些有益的研究, 但主要集中于较大颗粒(大于75 μm) 之间的规律, 而对颗粒较细的矿泥浆(小于75 微米级细颗粒占比70%~90%) 研究尚不完善; 且大多研究的是悬浮状态下的大颗粒迁移现象, 而对铝矿泥浆这种近流塑状态的土颗粒迁移情况研究较少。 因此, 有必要进一步研究微米级细颗粒颗粒级配、 内部结构性质对矿泥浆颗粒迁移影响规律, 以揭示矿泥浆内部颗粒迁移形成过程和发展的机理。 故研究尾矿泥颗粒中小于75 μm 的粒径组成规律是研究矿泥颗粒迁移规律的关键点之一。 目前, 由于传统土工试验测量中测试小于75 μm 细颗粒粒径的方法如密度计法、 移液管法受人为操作因素影响较大, 激光粒度仪的动态光散射测量被广泛用于测量颗粒级配的分析中[11], 动态光散射(DLS) 测量布朗运动, 并将此运动与粒径相关, 这是通过激光照射粒子, 分析散射光的光强波动实现的。 其基于米氏光散射理论, 其基本原理是: 激光被颗粒散射后, 其散射角与颗粒的直径呈反比, 通过探测器接收散射光的分布, 利用合适的光学模型和数学程序来获得待测颗粒的粒度分布[12], 例如丹东百特公司的Bettersize2600、 Bettersize3000 激光粒度分布仪等设备, 其颗粒粒径测量范围在0.02~2 600 μm, 基本满足小于75 μm 颗粒的测量要求。 本文依托于广西基金, 研究铝尾矿泥浆中微米级细颗粒的自然沉降规律, 为进一步研究颗粒迁移规律提供了一定的理论依据。
2 试验材料
试验矿泥取自平果铝厂洗矿车间排出后进入浓缩池之经初步沉淀的矿泥, 取回后利用软管排出上部析出水分后静置2~3 个月, 以模拟现场尾矿库的自然沉降情况, 经土工试验测得矿泥比重为2.628, 塑限为49.57%, 液限为73.15%, 塑性指数为25.56, 液性指数为33.76, 故该原状矿泥处于流塑状态, 矿泥如图1 所示。

图1 矿泥示意图Fig.1 Picture of slime
3 试验方法
3.1 桶内取样
由于矿泥浆呈流塑状态, 为了防止矿泥浆在取出时受扰动, 设计特制新型取样器, 取样器由推拉式活塞和两端开口的有机玻璃管组成, 有机玻璃管长40 cm, 直径15 mm, 表面粘贴刻度条以控制样品推出的量, 如图2 所示:

图2 矿泥取样Fig.2 Slime sampling
利用自制取样器进行连续取样, 并以每5 cm 划分缓缓将样品推出至不同的样品盒或烧杯备用。
3.2 含水率测试
含水率是矿泥的基本物理指标之一, 它反映矿泥的物理状态, 含水率的变化将使矿泥的一系列力学性质发生变化[13], 它是影响颗粒沉降、 迁移过程的重要指标之一, 矿泥浆经取样管取出后烘干、 计算得其含水率与深度关系如表1 所示。
3.3 矿泥预处理
向取出的矿泥中分别加入足量(1 000 mL 左右)的蒸馏水, 并向每组中分别加入4%的六偏磷酸钠(分散剂) 10 mL, 充分混合后按取样深度命名为7 组, 如表1 所示。 试验前, 利用电动搅拌机以1 500 r/min 搅拌10 min 后, 将混合液过75 μm 洗筛漏斗后进入烧杯, 并从烧杯中取少量悬浊液放入激光粒度仪进行测试。

表1 矿泥样品及含水率变化Table 1 Slime sample and moisture content change
4 试验结果与分析
4.1 激光粒度仪试验结果
将激光粒度仪的测试结果汇总, 画出颗粒级配曲线如图3, 对比2-1、 2-4、 2-5、 2-6、 2-7 可见, 在小于75 μm 粒径中, 矿泥中较大颗粒所占百分比随着深度降低而逐渐减小, 对比较底层矿泥2-1、 2-2,矿泥的级配曲线分别在较大粒径4.783 μm、 较小粒径0.078 μm 处相交, 在对比2-1、 2-3 可见, 矿泥的级配曲线分别在较大粒径2.360 μm、 较小粒径0.078 μm 处相交。

图3 矿泥浆颗粒级配曲线Fig.3 Slime particle grading curve
4.2 矿泥颗粒特征粒径与深度的相关性
由于矿泥取样为连续取样且取样段较短(5 cm),故可假定每组样内矿泥粒径组成均匀变化, 根据激光粒度仪试验结果, 将各深度矿泥的特征粒径统计如下图4 所示。 可见, 随着深度逐渐变大, 其有效粒径d10、 中值粒径d50、 及d90均呈现增大趋势, 其特征粒径和深度具有较好的正相关性且有效粒径d10在较深20~30 cm 处随着深度加深迅速增大, 而中位粒径d50在深度5~10 cm 段随着深度增加而有所减小。

图4 矿泥颗粒特征粒径-深度变化示意图Fig.4 Schematic diagram of characteristic size-depth variation of slime particles
4.3 矿泥含水率、 体积平均粒径与深度的关系
将不同深度的各组样品的含水率与其对应的体积平均粒径线性拟合可见, 矿泥浆含水率随深度加深逐渐降低, 由趋势线可见两者呈负线性相关, 线性拟合公式为y=-0.869 1x+136.84, 拟合度R2=0.732 2;而颗粒体积平均直径随深度逐渐上升, 由趋势线可见两者呈正线性相关, 线性拟合公式为y=0.156 2x+2.971 2, 拟合度R2=0.939 6, 如下图5 所示。
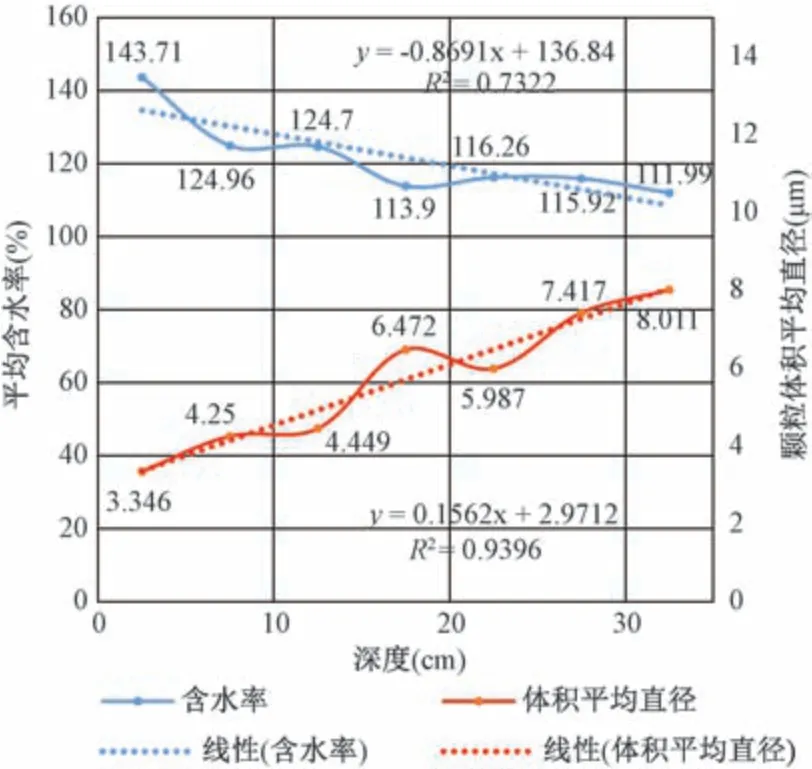
图5 含水率-体积平均径与深度拟合示意图Fig.5 Fitting diagram of water content-volume mean diameter and depth
4.4 颗粒沉降及矿泥分层讨论
为了便于计算, 假定矿泥颗粒为规则球体, 由于矿泥取回后静置数月, 桶内颗粒受重力、 介质浓度及机械阻力的影响。 由于矿粒的沉降末速同颗粒密度、形状有密切关系, 因此假定颗粒在流体中受到的力F, 则有:

其中:V为颗粒的体积;ρ和ρ0分别为颗粒和介质的密度;g为重力加速度。
当ρ >ρ0时, 颗粒下沉运动。 然而颗粒下沉时必会受到介质摩擦阻力, 随着颗粒不断运动, 其受到的阻力最终将等于F, 达到平衡, 即:

其中:v为颗粒的沉降速度;f为阻力系数。
对于球形颗粒, 由Stokes 定律可知, 阻力系数和介质黏度、 球体半径有关:

由球体体积计算公式:

简化得:

即为重力场中的沉降公式, 从式中可以看出: 沉降速度与颗粒半径的平方成正比, 与介质的黏度成反比, 颗粒的大小对沉降的速度影响较大, 在静置过程中, 相对较大的颗粒沉降速度更快, 聚集在底部[14](25~35 cm), 而更细的颗粒则悬浮在桶中层(15 ~25 cm) 或漂浮在表层(0~15 cm)。 桶体较下层由于颗粒的不断沉降, 其颗粒浓度不断增加, 相当于增加了介质的浓度, 由于颗粒间带电, 根据双电层理论,由于矿泥颗粒表面带电, 颗粒与颗粒之间受到静电斥力的作用而相互排斥, 而其之间又存在范德华力导致其存在吸引力, 当吸力大于斥力时, 颗粒间相互吸引, 团聚形成颗粒团, 反之则阻止颗粒团的形成, 阻止颗粒团沉降[15]。
而矿泥浆中富含大量的Al (OH)3, 在含水率高的泥浆中Al (OH)3可发生如下水解反应[16]:


其中:h为水解度,Kw为水的离子积,Kb为盐的电离常数,C为摩尔浓度。
由上文可知, 由于下层颗粒浓度不断增加, 相当于增加了介质的浓度, 即式(7) 中摩尔浓度C上升,而在一定温度下, 水的离子积常数和盐的电离常数为固定值, 则式(6) 反应向左移动, 生成的负电荷胶粒浓度降低, 从而减少颗粒与颗粒之间的静电斥力,则颗粒相互吸引、 团聚, 促使颗粒团体积变大, 因此底部(25~35 cm) 处其有效粒径迅速增大。
漂浮在表层的矿泥颗粒由于含水率较高, 细小矿泥颗粒间易受取样、 振动等因素扰动, 故表层区域0~5 cm 处中粒径存在一段减小的波动段, 而中间段过渡层, 矿泥颗粒介于表层段与沉降凝聚段之间, 受重力作用下, 矿泥颗粒呈较规律的随深度线性变化段, 符合Stokes 定律。
故可根据矿泥的沉降, 可将桶内的矿泥分为3层: 表层、 过渡层及沉降团聚层。
表层(0~15 cm): 颗粒粒径最小, 颗粒间距大,受扰动程度高。
过渡层(15~25 cm): 颗粒大小随深度呈正线性相关关系。
沉降团聚层(25~35 cm): 颗粒较大, 由于颗粒间距小、 浓度高, 影响带电粒子水解, 颗粒间斥力减小, 团聚沉降。
5 结论
本文从Stokes 定律及矿物颗粒水解的电平衡角度进行分析, 研究了自然沉降条件下微米级矿泥颗粒的沉降规律, 得出以下结论:
(1) 微米级矿泥颗粒的体积平均径与矿泥所处深度呈线性相关, 随深度增加矿泥颗粒的体积平均径呈线性增加, 其拟合度较高, 达R2=0.939 6, 故深度从一定程度上能够反映矿泥颗粒的变化情况。
(2) 根据双电层理论, 在较底层区域, 矿泥浆中由于微米级颗粒浓度的增加, Al (OH)3的水解反应向左移动, 使生成的带电胶粒浓度降低, 促进了矿泥颗粒间的团聚作用, 故底层相对于上部其有效粒径迅速增大。
(3) 由于在沉降过程中, 颗粒逐渐向下移动, 上部颗粒少, 含水率高, 故表层处颗粒易受扰动, 规律性较差, 而中间段, 矿泥颗粒呈较规律的随深度正线性相关, 因此将微米级铝尾矿泥颗粒受自然沉降过程中分为表层、 过渡层、 沉降团聚层3 层, 此分层可以一定程度上作为尾矿库中现场研究矿泥自然沉降情况的理论依据。
