基于大数据分析技术的云计算资源预测研究

卢思安，侯国庆

(1. 内蒙古农业大学计算机与信息工程学院，内蒙古 呼和浩特 010018；2. 内蒙古农业大学经济管理学院，内蒙古 呼和浩特 010018)

1 引言

在网络服务快速稳定发展的大环境下，云计算技术的应用随着计算资源需求量的提升而逐渐普及[1]，该技术以分布式并行计算、网络负载均衡、网格计算、网络存储等技术为核心[2]，通过云计算平台控制不同硬件设备协同运行，完成资源调度、业务访问与数据存储等功能，提升硬件设备工作效率[3]。作为资源调度的基础，云计算资源负载的预测领域云计算资源研究的主要内容之一[4]。

针对当前普遍使用的基于鲸鱼算法等云计算资源负载预测方法不能有效体现负载动态波动情况等问题[5]，研究基于大数据分析技术的云计算资源预测方法，利用混沌分析算法分析负载时间序列，生成学习样本，利用支持向量机构建预测模型，实现云计算资源的准确预测。

2 云计算资源预测方法

2.1 预测模型构建过程

基于大数据分析技术的云计算资源预测过程集合大数据分析技术中的时间序列混沌分析方法与支持向量机模型构建云计算资源预测模型，该模型构建过程如图1所示。

图1 云计算资源预测模型

云计算资源预测模型构建过程中，在海量云计算资源负载的时间序列数据内任意选取一个时间序列数据；采用时间序列混沌分析方法对所选数据进行预处理[6]，通过互相关方法确定时间序列相空间重构的最佳嵌入维和延迟时间；依照最佳嵌入维和延迟时间构建一个多维时间序列，将该多维时间序列作为学习样本；采用支持向量机训练学习样本，构建预测模型，实现海量数据预测。

2.2 时间序列混沌分析方法

以x={xi|i=1，2，…，N}表示一个初始云计算资源负载的时间序列，其中xi和N分别表示第i个样本和时间序列内的样本数量。依照塔肯斯理论[7]，经由判断嵌入维m与延迟时间t′能够确定初始云计算资源负载的时间序列的动力学特性[8]，公式描述如下：

(1)

式(1)内，M=N-(m-1)t′表示相空间内的点数。

分析式(1)得到，时间序列相空间重构的核心在于m与t′。确定m与t′的方法较多，但互相关方法具有较高的通用性[9]，利用该方法能够同时确定m值与t′值，由此在进行云计算资源负载时间序列数据相空间重构时的可采用互相关方法。

将初始云计算资源负载的时间序列分为子序列，利用式(2)描述互相关方法的关联积分

(2)

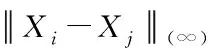
(3)

利用式(4)表示序列x={xi}的检验统计量

C(m，N，r，t)=C(m，N，r，t)-Cm(m，N，r，t)

(4)

式(4)内，r为x={xi}的半径。

划分x={xi|i=1，2，…，N}能够获取t个子序列，由此得到

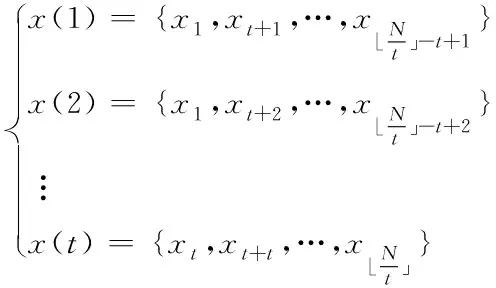
(5)

依据分块均值方法确定式(5)的统计量[10]，公式描述如下

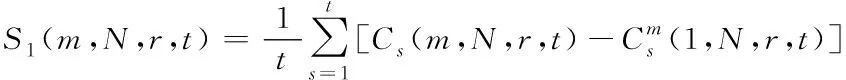
(6)

式(6)内，r表示随机两点间的距离。

设定N→∞，由此得到

(7)

在x={xi|i=1，2，…，N}长度无穷大的条件下，所有S(m，r，t)值为0，但现实环境里，x={xi|i=1，2，…，N}长度并不是无穷大的，所以S(m，r，t)值不为0，通过局部最大时间间隔法确定r最小的时间点[11]，得到

ΔS1(m，t)=max{S1(m，rj，t，N)}

min{S1(m，rj，t，N)}

(8)

使(8)内，rj表示第j个半径值。

由式(8)得到，最佳t′为ΔS1(m，t)—t间第一个局部极小值，由此可得

(9)

(10)

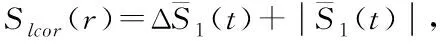
t′w=(m-1)t′

(11)

依照最佳嵌入维和延迟时间构建一个多维时间序列，以此为学习样本利用支持向量机训练学习样本，构建预测模型，完成预测目的。

2.3 支持向量机

以∂(x)表示非线性映射函数，利用∂(x)将学习样本映射至高维特征空间内[12]，在高维空间内实施线性回归处理，以式(12)表示支持向量机回归函数

f(x)=w·∂(x)+b

(12)

式(12)内，w和b分别表示权向量和偏置向量。依照最低风险需求[13]，利用式(13)所示的优化问题描述式(12)

(13)

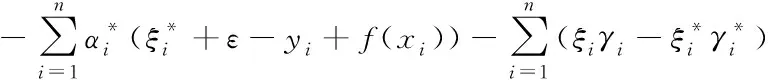
(14)

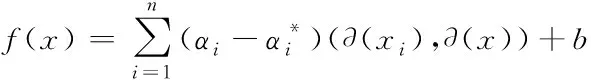
(15)

利用核函数K(xi，x)取代(∂(xi)，∂(x))，得到

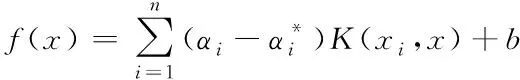
(16)

选取径向基核函数作为支持向量机核函数，由此得到：

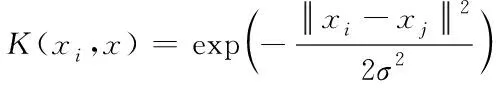
(17)

式(17)内，σ表示径向基核函数宽度参数。

由式(16)、(17)得到，通过确定最优支持向量两个参数H和σ，确定相应的f(x)函数值，即可实现云计算资源负载预测模型构建的目的。参数H和σ直接影响模型的质量，因此采用蝙蝠算法[15]优化参数H和σ，具体优化过程如图2所示。

图2 蝙蝠算法优化支持向量机模型参数过程

3 测试分析

实验为验证本文所研究的基于大数据分析技术的云计算资源预测方法的应用性，选取某云计算系统内CPU单分钟内的负载历史数据为测试对象，其具体情况如图3所示。采用MATLAB软件为仿真工具，验证本文方法的应用性。

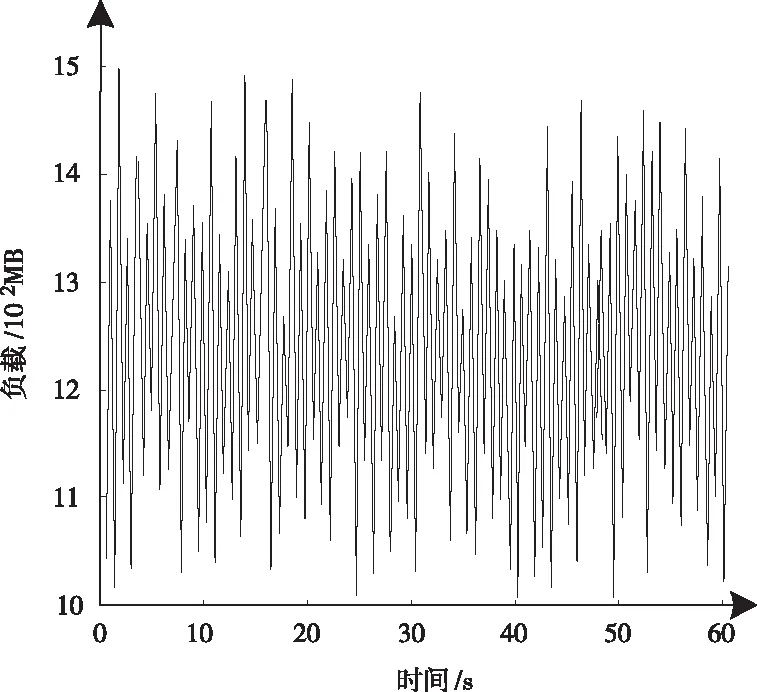
图3 测试对象图

3.1 测试对象时间序列分析

Lyapunov指数法是一种定性分析时间序列的混沌性方法，采用该方法分析测试对象混沌特性，通过傅立叶变换处理测试对象，确定测试对象平均轨道周期。利用本文方法确定测试对象的最佳嵌入维与延迟时间，获取重构后的测试对象多维时间序列。确定序列内各点的离散时间和邻近点距离，并求解均值。

通过上述过程确定Lyapunov指数为0.0996，该值大于0，因此能够说明图3所示的测试对象存在混沌特性。采用本文方法分析测试对象的最佳嵌入维与延迟时间所得结果如图4所示。由此得到，最佳延迟时间为8，最佳嵌入窗为12，据此得到最优嵌入维数为3。

3.2 预测结果

以测试对象时间序列分析所得的各项参数为基础构建测试对象负载学习样本，以图3内数据的最后10s为测试样本，钱50s数据点为训练样本进行学习，构建预测模型，进行单步预测和多步预测，所得结果如图5所示。

分析图5(a)内的单步预测结果得到，本文模型能够有效地跟踪测试对象的变化趋势，获取高精度的测试对象预测结果。

图5 预测结果

由于云计算资源负载预测的主要目的是预测未来固定时间内负载的波动情况，而单步预测的结果通常仅体现下一时刻负载的情况，无法体现长时间的波动情况，因此需要进行多步预测。

分析图5(b)所示的多步预测结果得到，采用本文方法进行多步预测所得结果与单步预测所得结果相比较差，但依旧能够较好地呈现测试对象的波动情况，预测结果能够为测试对象管理提供有效的辅助。

3.3 预测能力

以平均绝对误差、均方根误差、均方误差和均方根误差为评价指标，评价本文方法对1小时和2小时间隔的预测结果，所得结果如表1所示。

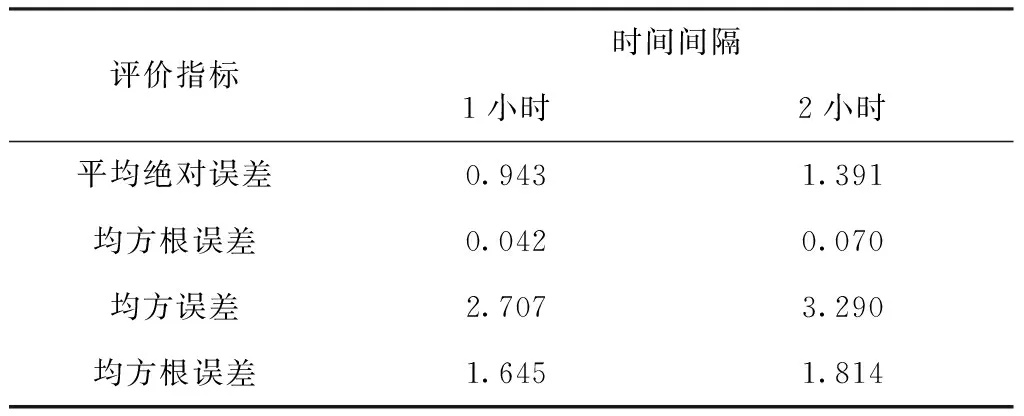
表1 不同时间间隔的预测结果

分析表1得到，在不同时间间隔条件下，本文方法均可精准地预测测试对象负载值，由此说明本文方法具有较好的泛化能力。

4 结论

本文研究基于大数据分析技术的云计算资源预测方法，对云计算资源负载进行预测，所得结果显示本文方法能够准确预测短时间内的负载情况，而针对长时间的负载预测也能够得到较好的效果，预测结果能够为测试对象管理提供有效的辅助。