渡槽流态优化数值模型构建与流态复原验证分析
2022-11-29马山玉王志刚屈志刚葛均建
马山玉,李 钊,王志刚,屈志刚,葛均建
(1.河南省水利勘测设计研究有限公司,河南 郑州 450016;2.中国南水北调集团中线有限公司河南分公司,河南 郑州 450016)
1 引言
南水北调中线工程是跨地区、跨流域的特大型调水工程,全线采用水头自流输水。2020 年4 月末,中线工程开启运行以来第一次大流量输水,大流量输水期间,中线工程澧河渡槽等渡槽的槽内及出口出现流态紊乱现象,槽内水位异常波动,渡槽出口出现明显的卡门涡街现象[1],一定程度上制约了中线工程的调水能力,影响了工程运行安全和效益发挥,亟需研究流态紊乱的原因并提出流态优化工程措施。
目前研究水工建筑物流态的方法主要包括理论分析、原型观测、模型试验及数值模拟四种方法。数值模拟方法是利用软件直接求解方程,不但可以直观模拟各种水力学现象,而且具备模拟方案修改灵活、研究周期短、可重复性好、可视化效果好、能较快地模拟出定性和定量的流场结果等独特的优势。
为还原澧河渡槽加大流量下的流态现象,分析流态紊乱的原因,拟采用三维水动力学数值模拟方法,通过按1∶1比例对澧河渡槽及进出口一定范围内的渠道进行精确BIM建模,采用2020 年6 月11 日现场观测结果作为边界条件,对澧河渡槽当天的流态现象进行数值复演模拟,通过在同一工况下将现场观测流态与数值模拟结果进行对比,可验证数值模型的准确性和可靠性,验证模型的准确性和网格剖分的合理性,从而为后续流态优化方案模拟打下基础,为流态优化工程措施准备最佳的数值计算模型。
2 模型原理
三维数模基于流体力学基本方程组构建,采用两方程RNGk-ε紊流模型[2-4],其控制方程见式(1)~式(4):
式中:ρ为混合流体的密度;t为时间;xi、xj为坐标分量;ui是xi方向的瞬时速度分量,i,j=1,2,3;p为修正压力;k为紊动能,ε为紊动消耗率;为流体动力粘度,t为黏流黏滞系数;G为经验常数,一般取0.09;σk和σε为k和ε的紊流普朗特数。
G为由平均速度梯度引起的紊动能产生项,即:
式中:αW为水的体积分数ρ,W和ρa分别为水和空气密度,w和分别为水和空气的分子黏性系数。
目前在计算流体力学中,离散方法主要包括有限单元法(FEM)、有限差分法(FDM)、有限体积法(FVM)等,均有各自的优缺点,有限体积法的基本原理是通过将计算区域划分为一系列连续的控制体积,而离散方程是通过在每个控制体上对方程进行积分所得。有限体积法相比于其它方法有一定的优势,这种方法的计算量较小,应用较为广泛,适用于任意复杂几何边界,因此作为本次数值模拟采用模型求解方法。
3 三维水动力学数值模型构建
3.1 模型范围拟定
澧河渡槽研究核心是渡槽进出口及槽身,但考虑到渡槽对上下游的影响,故将模型范围向上下游进一步延伸,再考虑到计算量、模型精度以及电脑性能瓶颈,模型范围拟定为澧河渡槽进口上游200 m至出口下游200 m,设计桩号209+184~210+320,全长1136 m,包括:前段明渠200 m,进口渐变段45 m,进口节制闸26 m,进口过渡段20 m,渡槽槽身段540 m,出口过渡段20 m,出口检修闸15 m,出口渐变段70 m,出口明渠段200 m。
3.2 工程BIM模型构建
为构建三维水动力学数值分析模型,先采用三维设计软件构建模型范围内的工程三维BIM模型,本次软件按1∶1比例按原尺寸和高程精确构建了澧河渡槽工程BIM模型,通过反复检查,任意部位模型尺寸和高程精度均控制在1 mm以内,BIM模型见图1。

图1 澧河渡槽BIM模型
3.3 网格剖分
在数值模拟计算的过程中,网格剖分需同时满足项目计算精度和计算效率要求。为此,进行网格剖分实验,以验证网格收敛性与无关性,并确定合适的网格剖分尺寸,最后再采用推荐的尺寸对最终模型进行网格剖分。
3.3.1 网格收敛性与无关性实验
选取澧河渡槽出口部分渠段作为实验模型的建模范围,总长405 m,包括100 m渡槽、35m过渡段和闸室段、70 m出口渐变段和200 m后段明渠,分别采用0.6 m、0.4 m和0.2 m尺寸进行网格剖分,构建3 组实验模型,每组实验模型均采用统一的边界条件和参数,进口采用流量+水位边界条件,给定进口设计流量320 m3/s和进口水位133.88 m,出口采用压力边界条件,给定设计水位134.11 m。最终3 组实验模型网格剖分数量分别为1256 万、227 万、73 万,通过对3 组实验模型进行模拟计算,以验证网格疏密程度对流态的影响。具体网格的划分情况见图2,各实验模型GCI的计算结果见表1。

表1 3组实验模型GCI计算结果

图2 3组实验模型网格剖分图
分析表2 数据,不同网格方案模拟的断面平均水深相差较小,相对误差均在0.3%以内,最大与最小值差异在1 cm以内,可见网格剖分尺寸不同并不会显著影响模拟结果,可确认网格的无关性。结合表1与表2的结果,并考虑到计算效率及计算机的内存限制,推荐渡槽流态优化数值计算模型主要以0.4 m为尺度的网格剖分方案。
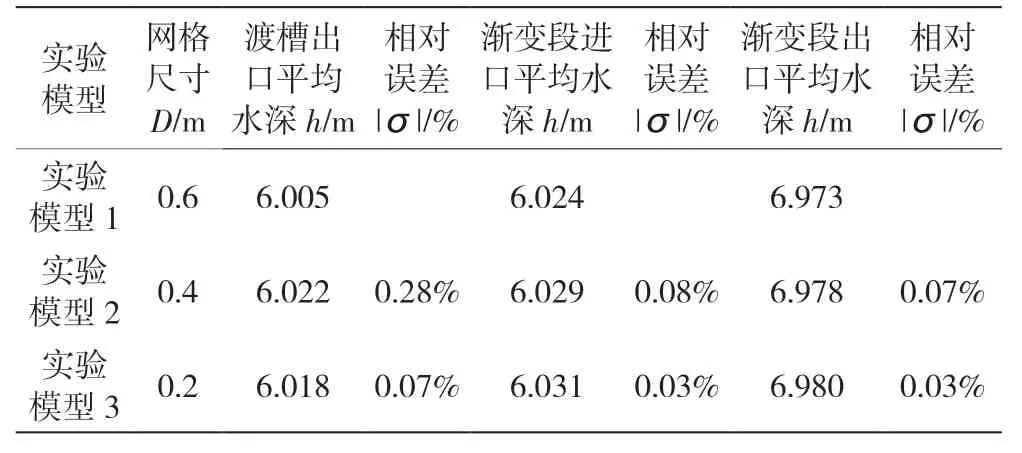
表2 3套实验模型特征断面平均水深
3.3.2 澧河渡槽数值模型网格剖分
在划分网格时,应遵循网格划分疏密适当的原则,在研究关键部位和流态剧烈变化的部位,网格剖分应更密一些,次要部位网格则疏一些,以便于更好地捕捉自由水面以及水流流动情况。
通过网格收敛性与无关性实验结果,本次以0.4 m网格尺寸为基准,对不同工程部位采用不同的网格剖分尺寸,其中进出口明渠及槽身部位采用0.5 m网格剖分,进出口渐变段、闸室段和过渡段采用0.4 m网格剖分,局部墩头位置采用嵌套网格加密到0.2 m,整个模型划分网格总数为382 万。
为使计算结果加速收敛,整个模型全部采用结构化网格。为减少网格数量,网格划分根据工程各部位范围分块分区进行,分别为:上游明渠区、进口渐变段和闸室段区、渡槽区、出口闸室段和渐变段区、下游明渠区。典型网格剖分见图3。

图3 澧河渡槽水动力学数值模型典型网格剖分
3.4 边界条件及其他参数设置
为准确还原6 月11 日当日流态,各边界条件参数均采用当日18 时实测参数,分别为:
(1)进口边界条件
进口边界条件设置在上游明渠入口断面位置,采用当日实测流量350.34 m3/s,为准确还原当日进口水位和流速,对该边界条件还额外附加了水位条件限制,水位采用当日进口实测水位135.12 m,流量和水位均采用恒定值,在整个模拟过程中保持不变。
(2)出口边界条件
出口边界条件设置在下游明渠出口断面位置,采用压力出口边界条件类型,给定一个标准大气压和水位134.67 m,及当日实测的下游出口水位。
(3)其他边界条件
整个模型上部开放区域为空气与水接触的开放区域,设置为压力边界条件,给定一个标准大气压;模型左右侧和底部为渠道或渡槽混凝土构建,给定壁面边界条件,并定义为无滑移固壁边界条件,近壁采用标准壁面函数,壁面法向速度为零。
(4)其他参数设置
将初始条件设置为与边界条件相匹配的水位,即进口水位采用135.12 m,出口水位采用134.67 m,由此形成初始水体域,并给定初始流速1.173 m/s,使其初始流量等于入口边界条件流量。
糙率设置:模型糙率与项目初步设计时采用的一致,即渠道采用综合糙率0.015,渡槽采用糙率0.014。
模拟时间步长设置由模型收敛性决定,在模拟过程中可实时调整,对于难以收敛的计算步采用更小的时间步长,否则则增大时间步长以提高计算效率,初始时间步长设置为0.005 s。
输出设置,输出包括任意位置的水位、水深、流速、压强、湍流强度、动水压力等各项参数,此外单独增加了3 个虚拟挡板,用于统计通过左右渡槽和渠道的流量、平均流速、总水头等,结果输出时间步长统一设为1 s。
4 模拟结果与现场观测对比
通过利用三维水动力学数值分析模型对2020 年6 月11日澧河渡槽流态进行模拟,较好地还原了当时澧河渡槽各种流态,模拟了现状流态形成的原因。
4.1 进口流态模拟结果
进口节制闸前水位呈周期性波动,最大波幅约0.5 m,波动周期9 s,左右两槽水面波动存在相反相位差,即一槽出现波峰时另一槽刚好为波谷[1],节制闸前水位波动见图4。
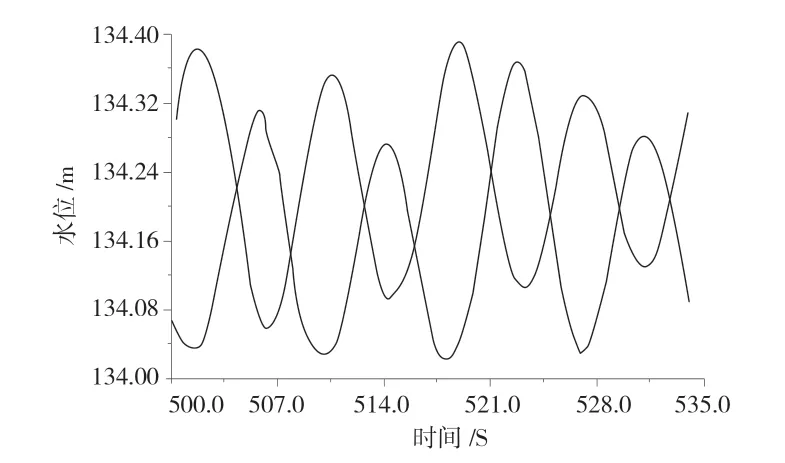
图4 渡槽进口节制闸前水位波动
由于进口中墩墩头宽平,渠水急剧绕流,使得墩头前小范围流速降低,水位则略有雍高,而墩头后两侧水位迅速降低,形成一个水位的“凹坑”,相比墩头水位骤降约0.7 m左右,而在“凹坑”中心处流速则达到最高3.3 m/s左右,“凹坑”下游墩壁两侧则出现一定范围的局部水跃现象。进口流态见图5,现场观测渡槽进口流态见图6。

图5 数值模拟渡槽进口流态

图6 现场观测渡槽进口流态
4.2 出口流态模拟结果
出口模拟结果显示:由于出口墩头宽平,渠水急剧绕流,使得墩头后流态紊乱,左右两槽水流以中隔墩为中心,呈周期性摆动现象,摆动周期约为9 s,摆动还伴随有方向相反的局部涡流向下游传递,即呈现出流体力学中典型的”卡门涡街”现象,随着墩头下游尾涡的摆动,下游渐变段及一定范围内的渠道水位也随着波动,在渐变段出口左右两侧的拐点位置出现局部涡流现象。模拟流态见图7,出口流出见图8,现场观测渡槽出口流态见图9。
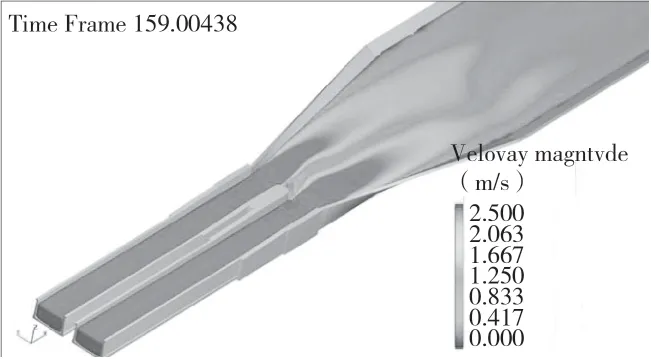
图7 数值模拟渡槽出口流态图

图8 数值模拟渡槽出口流场图

图9 现场观测渡槽出口流态图
4.3 槽身段模拟结果
槽身段模拟结果显示:渡槽内出现超常的水面大波动现象,左右两槽波动相位差异呈现随机性,并偶尔出现间歇性横梁阻水和局部漫槽现象,数值模拟结果见图10。现场观测渡槽槽身流态见图11。

图10 渡槽内水位异常波动现象

图11 渡槽内水位异常波动现象
5 结论
通过数值模型复原模拟的渡槽进出口流态、水位波动周期等与澧河渡槽当日现实观测结果完全一致,数值模拟的渡槽槽身横梁阻水和漫槽现象也呈现周期性、随机性,与现实观测结果基本一致。因此,构建的数值模型及网格剖分合理,可用于澧河渡槽流态优化措施研究,也可为类似流态优化项目数值模型构建提供借鉴。
